磁粉制动器的模糊神经元PID控制

金 昊，白国振，朱灵康，杨 雷

(上海理工大学 机械工程学院，上海 200093)



磁粉制动器的模糊神经元PID控制

金 昊，白国振，朱灵康，杨 雷

(上海理工大学 机械工程学院，上海 200093)

针对磁粉制动器扭矩加载系统的非线性和不确定性问题，提出了一种模糊单神经元复合智能控制的方法。通过单神经元学习算法进行参数自整定，实现单神经元控制器输出增益的实时调节。结合仿真及扭矩加载实验进行验证和比较，结果表明，基于模糊单神经元PID控制器能有效地改善磁粉制动器加载控制性能。

磁粉制动器；扭矩加载；智能控制；单神经元控制器；模糊神经元

常规的PID 控制不仅需要被控对象的精确数学模型，且控制参数无法实时调节，因而对一些时变性、非线性、不确定性的复杂对象的控制效果欠佳，无法满足工程需要。为此，本文提出采用单神经元自适应PID控制器来代替常规的增量式 PID 控制器，以改善控制性能。并在改进单神经元控制器学习算法的基础上引入了模糊控制技术，用以实现单神经元控制器输出比例系数的自整定，从而进一步提升单神经元PID控制器的性能[1]。

1 模糊神经元PID控制器设计

1.1 单神经元自适应PID控制器

单神经元PID控制器是一种结构简单的自适应智能控制器，它具有权值学习快速、计算量小、易于实现的优点，而且能适应外部环境变化，具有较强的鲁棒性[2]。单神经元自适应控制器的控制原理，是通过良好的学习算法对加权系数进行调整，以此来实现自适应、自组织的功能。其加权权系数的学习规则多种多样，常见的有无监督Hebb学习规则、有监督Delta学习规则以及有监督的Hebb学习规则。其控制算法及按有监督的Hebb学习规则实现的学习算法为[3]

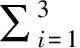
(1)

(2)

(3)

式中，x(k)=e(k)；x(k)=e(k)-e(k-1)；x(k)=e(k)-2e(k-1)+e(k-2)；z(k)=e(k)；ηI,ηP,ηD分别为积分、比例、微分的学习速率，K为神经元的比例系数，K>0。u(k)为单神经元的输出，k为采样时间，i=1,2,3。

将ηI,ηP,ηD设定为不同值，用以区分积分、比例、微分作用的权值系数的调整过程。而神经元的输出比例系数K值的选取尤为重要，必须适中。K值太小，系统会无法及时响应，快速性得不到保证。但K值太大，又会使系统的超调量过大，产生震荡，且难以达到稳态。 所以适合的K值很重要[4]。

1.2 单神经元自适应PID控制的改进

根据最优控制的理论，采用二次型性能指标来计算神经元的控制规律，优化神经元的学习算法，从而得到所期望的优化效果。具体做法如下：引入二次型性能指标来改进加权系数的学习算法，通过使输出误差与控制量加权平方和达到最小来调整神经元的加权系数，从而实现对被控对象输出误差的控制。采用基于二次型性能指标学习算法的单神经元自适应PID控制器结构描述为[5]：

设性能指标为

(4)

式中，P和Q分别表示输入误差和控制量的加权比例系数，r(k),y(k)为k时刻的参考输入和实际输出。

单神经元的学习法则变为

(5)

式中，b0为输出响应的第一个值。

1.3 输出增益系数K的模糊自整定

结合模糊控制技术，设计一个二维模糊控制器，用于对单神经元控制器的输出增益K实现参数自整定。根据模糊自适应原理，由不同时刻的误差e(t)和误差变化Δe(t)来推导出不同的KP，KI，KD值，从而使系统更加快速稳定的趋于设定值[6]。则式(5)变为

(5)

文中二维模糊控制器的两个输入变量为E和Ec，分别代表扭矩误差和误差变化率所对应的模糊量，这是因为工程应用中，只需要PI控制器就可以对磁粉制动器的扭矩进行良好的控制，所以本文只设计了模糊单神经元PI控制器。

两个输出控制量为KI,KP，相应语言变量论域为[7]

E,Ec,KI,KP={ -3, -2, -1, 0, 1, 2 , 3 }；

在其论域上取7个模糊子集:NB, NM, NS, Z, PS, PM, PB，分别代表负大，负中，负小，零，正小，正中，正大。E和Ec的隶属度函数如图1所示。

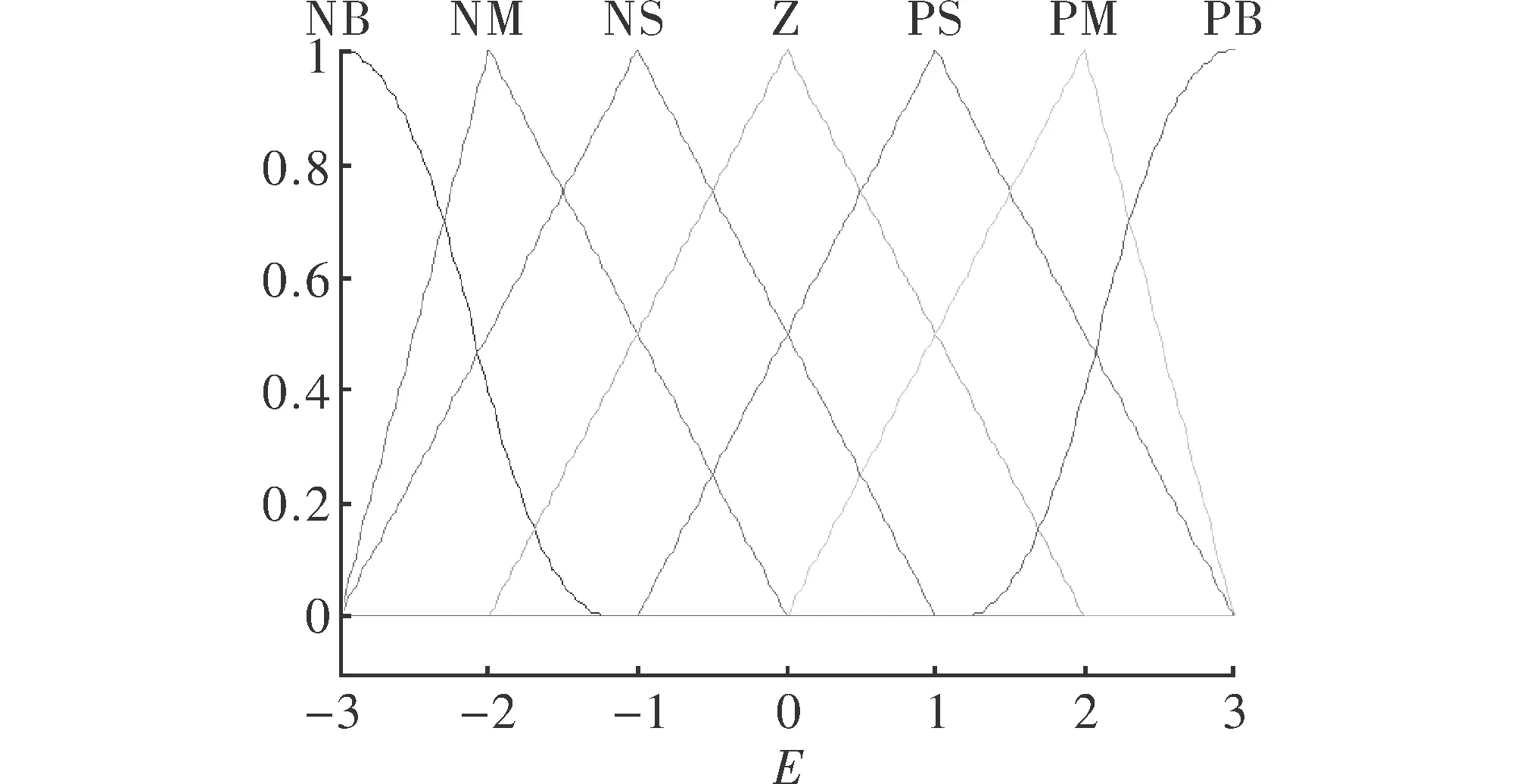
图1 输入和输出变量的隶属函数曲线

表1给出了模糊控制规则表，单神经元本质上是增量式PID，其KP的选取规则为在误差很小时，加大KP，误差过大时减小KP。KI的模糊规则选取标准为：当响应在上升过程时，此时系统误差较大，允许KI值较大，以获取更快的响应速度，从而缩短调节时间；而当误差持续减小接近0时，则应当选择较小的KI值，以避免超调，提高系统稳态性能；当超调时，应当降低KI。本文采用经典的 Mamdani Max-Mi合成法进行模糊推理[8]，方法如下：

以误差和误差变化为前提，第ij条模糊规则的表达形式为

Ruleij:ifF=uiandEc=ujthenu=uij

(7)

采用乘积推理机，规则前部分的隶属函数为

fij=μi(E)μj(Ec)

(8)

采用重心法进行反模糊化，得到模糊控制器[9]

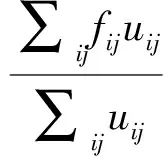
(9)

uij的值由模糊规则表1[10]确定。

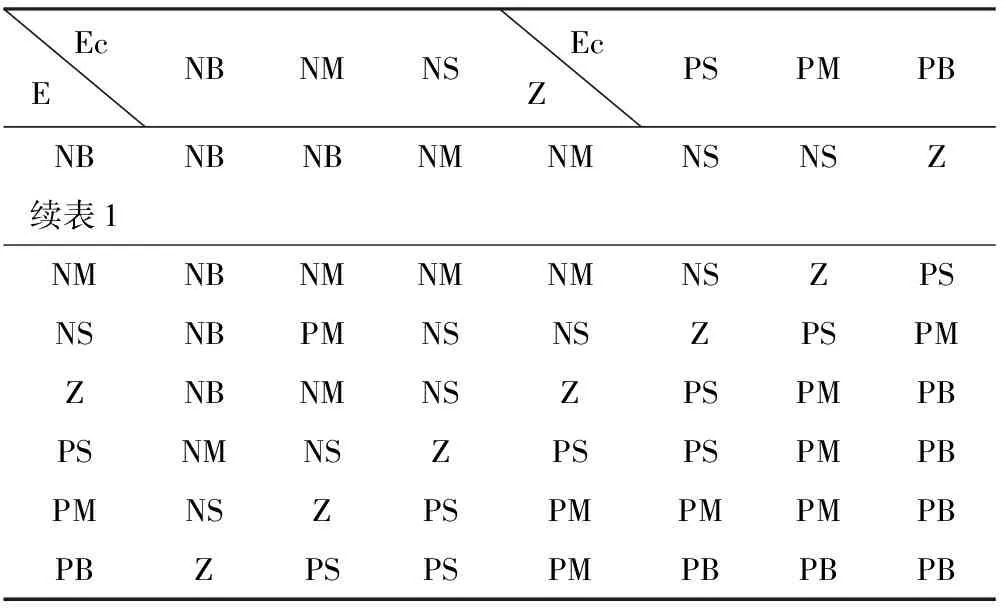
表1 KI的模糊控制规则

2 Matlab/Simulink仿真

针对上述扭矩加载系统简化的二阶SISO模型进行Simulink仿真。由于在工程应用中，只需要PI控制器就可以对磁粉制动器的扭矩进行良好的控制，所以仿真实验中，都采用模糊单神经元PI控制器。Simulink仿真结构如图2所示，其中单神经元PI控制器采用S函数编写，模糊规则使用Simulink模糊工具箱编写。

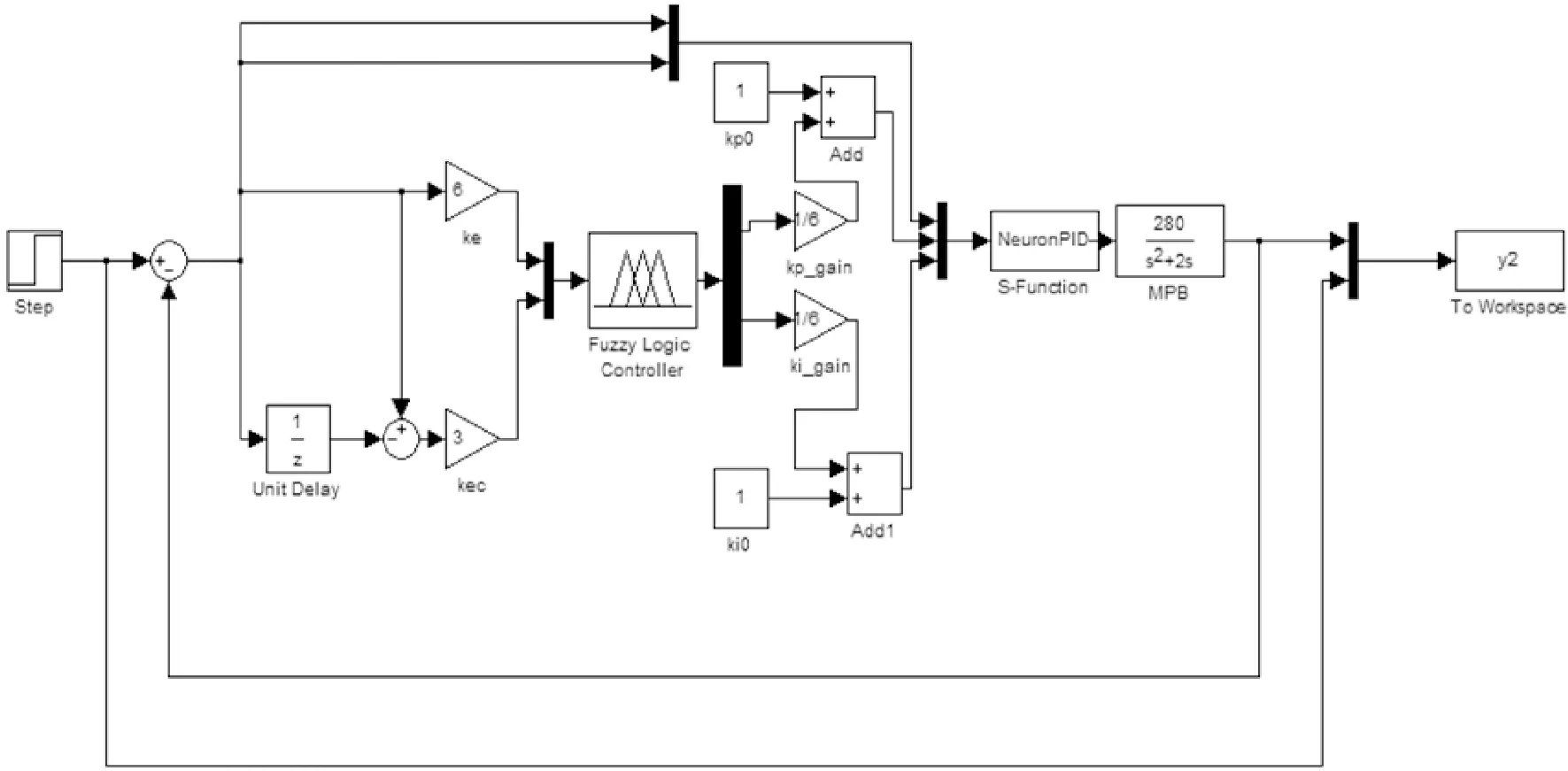
图2 模糊单神经元PI仿真结构图

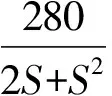
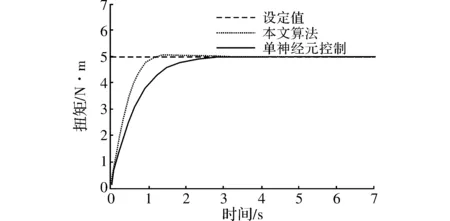
图3 阶跃信号仿真图

从图3中可知，模糊单神经元PI控制机器响应时间为1.2 s，较单神经元控制器2 s的响应时间有较大改善，可以更快地达到稳态，控制性能改善明显。

3 扭矩加载实验

为证明本文设计的模糊单神经元PI控制器的实用性，建立了基于磁粉制动器的扭矩加载实验台，使用ST语言编写控制算法[8]。本文所使用的加载伺服系统是基于磁粉制动器的扭矩加载试验系统，如图4所示。

图4 磁粉制动器扭矩加载试验台

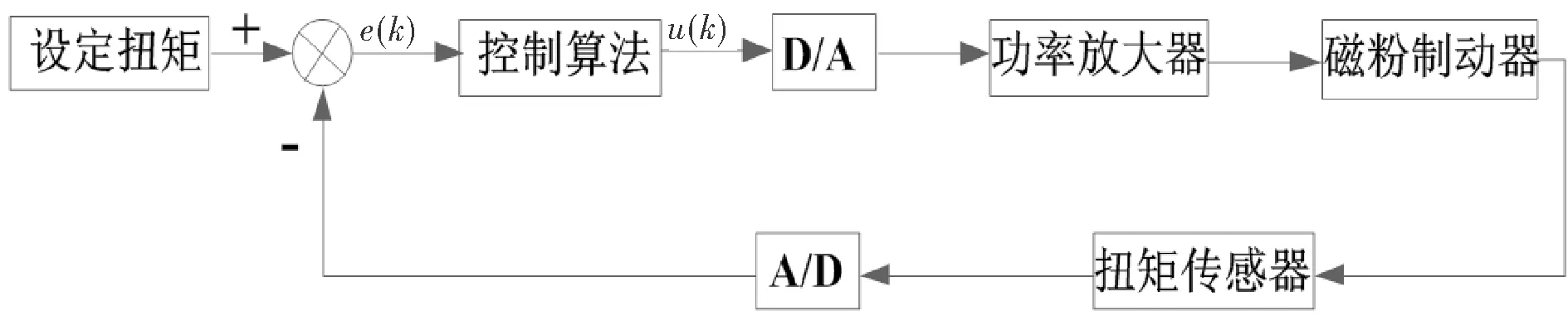
图5 磁粉制动器扭矩加载系统控制流程图

整个系统的控制过程如图5所示，通过控制算法得到相应的控制量，从而对系统实现控制，最终使设定扭矩与实际测得值之差趋于零，进而实现输出扭矩的轨迹控制。 本次实验先后给磁粉制动器加载阶跃、方波、正弦波的扭矩信号，比较本文设计的控制器与普通单神经元PI控制器的跟踪效果。伺服电机的转速为100 r/min，采样周期均为1 ms。

3.1 恒值加载

图6给出了采用单神经元及本文算法控制的系统扭矩阶跃响应曲线，其中，加载扭矩为恒值5 N·m。如图6所示，虽然两种算法最终都可以跟上给定值，但是本文模糊神经元PI算法的响应时间为1.3 s，单神经元算法的响应时间为2.3 s。提升了1 s的响应时间，从而使系统更快达到稳态。

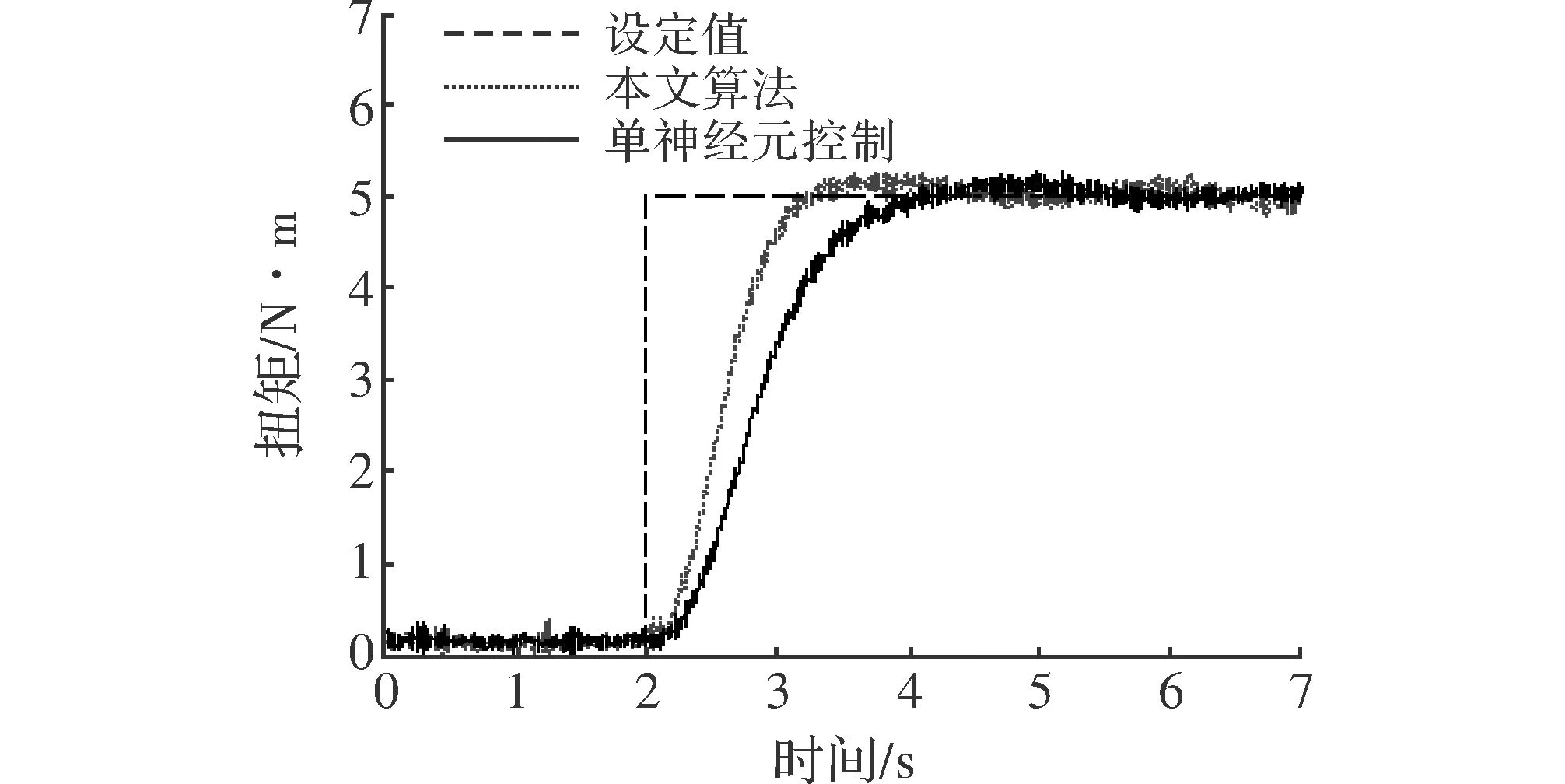
图6 恒值加载时系统扭矩响应曲线

3.2 方波加载

给定幅值为5 N·m，加载周期为4 s的扭矩曲线，系统的扭矩响应曲线如图7所示。由实验响应的波形图可以看出，本文所提算法具有更好的跟随性。对方波这种对跟随性要求高的波形，显然本文算法较普通单神经元控制有了明显改善。

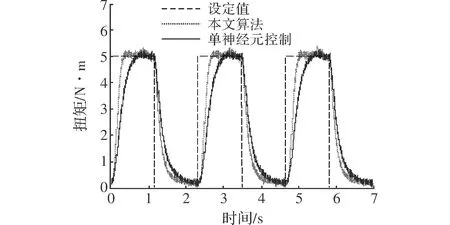
图7 方波加载时系统响应曲线

3.3 正弦加载

实验加载幅值为5 N·m，周期为5 s的正弦扭矩曲线。图8给出了正弦加载时系统的扭矩响应曲线。由图可知，本文算法可以快速跟上给定信号，延迟时间比普通单神经元控制器小，性能更加优越。

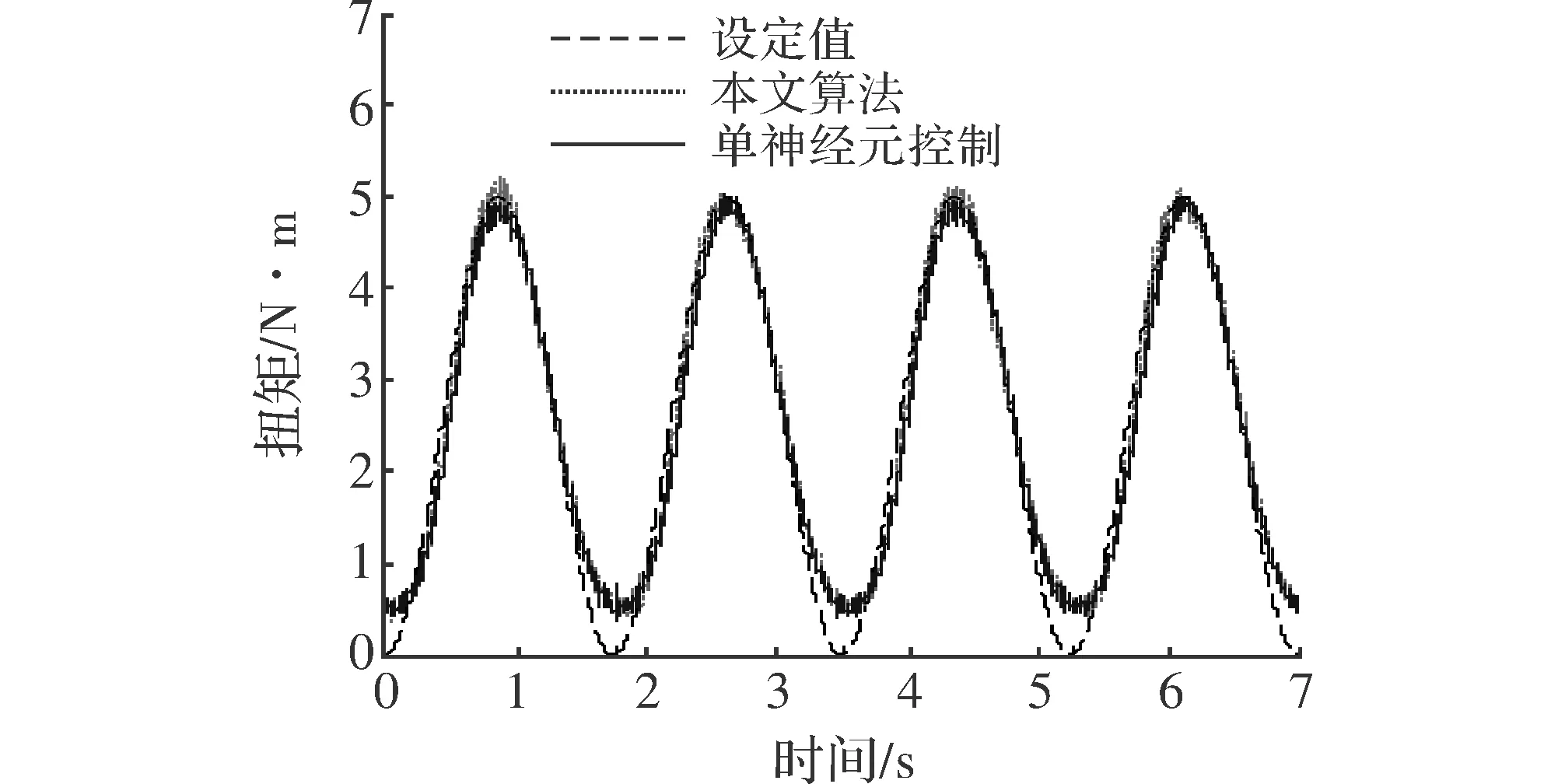
图8 正弦加载时系统响应曲线

4 结束语

(1)本文针对磁粉制动器扭矩加载系统的非线性和不确定性，建立了二阶SISO系统模型，在此基础上提出了一种结合单神经元控制技术和模糊控制技术的复合控制技术，以此来改善磁粉制动器的扭矩加载特性；

(2)建立了基于MatlabSimulink的扭矩加载系统仿真，验证了本文提出的模糊单神经元算法的可行性和有效性；

(3)在仿真的基础上搭建磁粉制动器扭矩加载实验平台，并成功进行了加载实验。将实验结果与普通单神经元控制算法相比较，结果表明本文算法对加载系统性能有了明显提升，克服了磁粉制动器扭矩加载系统的非线性和不确定性。

[1] 王卫星,鲁楠,傅立思,等.单片机控制磁粉制动器模拟加载系统的研究(第Ⅰ报) 磁粉制动器性能试验及控制系统设计与分析[J].农业工程学报,1996(1):1-7.

[2] 刘京亮,宋影,刘飞,等.磁粉制动器加载特性研究[J].航空精密制造技术,2013(2):59-62.

[3] 张玉存.Hopfield神经网络在磁粉制动器设计中的应用[J].系统工程与电子技术,2005, 27(12):2083-2085.

[4] 肖宝平,单越康.一种实用恒张力控制系统的研究[J].中国计量学院学报,2006,17(4):277-280.

[5] 王力,钱林方.磁粉制动器的建模与辨识研究[J].电气自动化,2010,32(5):55-58.

[6] 李宝福,陈敏贤.克服磁粉制动器低速爬行的自动控制方法[J].机械制造,2000,38(3):19-22.

[7] 穆安乐,原大宁,邹信用,等.面向混合驱动实验平台加载的磁粉制动器磁滞特性研究[J].西安理工大学学报,2008,24(1):58-61.

[8] 盛新.模糊-PID在高速切纸机张力控制中的应用[D].济南:山东轻工业学院,2009.

[9] 刘金琨.先进PID控制Matlab仿真[M].北京:电子工业出版社,2011.

[10] 张建民,王涛,王忠礼.智能控制原理和应用[M].北京:冶金工业出版社,2003.

Fuzzy Neural PID Control of the Magnetic Particle Brake

JIN Hao, BAI Guozhen, ZHU Lingkang, YANG Lei

(School of Mechanical Engineering, University of Shanghai for Science & Technology, Shanghai 200093, China)

In order to solve the nonlinearity and uncertainty of magnetic powder brake (MPB) torque loading system, we propose a method for fuzzy single neuron intelligent controller (FSNC) to improve the control accuracy. It combines the advantages of the fuzzy controller and the single neuron controller (SNC), without the need for an accurate mathematical model of controlled objects. It is capable both of auto-tuning parameter by the effective single neuron learning algorithm, and of timely adjustment of the output gain of a single neuron controller using the fuzzy control technology. So the FSNC has a strong real-time performance, immunity of interference and robustness. Based on modeling and simulation on Matlab, we establish an experimental torque loading system based on MPB. Then we step through each load, square wave, sine wave torque to compare the fuzzy single neuron algorithm and ordinary single neuron algorithm. Experimental results show that the fuzzy single neuron PID controller can effectively improve the performance of MPB load control to offer good static and dynamic performance.

magnetic powder brakes; torque load; single neuron controller; fuzzy neuron

2016- 09- 22

金昊(1982-)，男，硕士研究生。研究方向：永磁无刷直流电机。

10.16180/j.cnki.issn1007-7820.2017.07.011

TP273

A

1007-7820(2017)07-040-04