基于随机波动模型的双障碍期权问题的研究

□刘兆莹 孟乃杰 柏 松 王天珊

（华北理工大学 河北 唐山 063000）

基于随机波动模型的双障碍期权问题的研究

□刘兆莹 孟乃杰 柏 松 王天珊

（华北理工大学 河北 唐山 063000）

本文首先建立随机波动下的双障碍期权定价问题的模型，进而推导出了关于期权价格的偏微分方程。力图证明现实的金融市场中,有效的市场模型对于投资者决策以及金融风险管理和避险等方面有着重要的影响。

双障碍；期权；偏微分方程；金融风险

期权交易在经济领域中有重要意义，由于障碍期权可以作为一种防范风险有效手段，近年来发展迅速，是金融数学中的前沿课题之一。

所谓障碍期权，就是为了减少风险而施加了限制的一种特殊期权。双障碍期权同时具有高障碍和低障碍，或者说敲出期权和敲入期权。敲出期权就是当标的资产价格达到某障碍水平时，该期权作废；敲入期权就是当标的资产价格达到某障碍水平时，该期权生效。也就是说，双障碍期权是两个相互依赖的敲出期权和敲入期权的结合体，一旦潜在资产达到低障碍，敲入期权立即使其生效；反之，潜在资产超出高障碍，敲出期权立即使其失效。

双障碍期权已经成为金融市场上的热门问题，是单障碍期权问题的扩展形式。障碍期权问题之所以热门，原因之一就是比标准期权廉价，而且在用作套期保值时有同等级别的保护。

期权障碍是由Merton于1973年首次提出，给出了连续监测下的更低敲出边界的期权定价公式；而后Goldman等于1979年给出了路径依赖型的期权定价公式。此后，Rich[1]和 Rubinstein-Reiner[2]于上世纪 90年代在等价鞅测度下使用概率方法，给出了欧洲单障碍期权的定价公式。

本文考虑双障碍期权问题的基础资产模型。实证表明了股票期权具有隐含波动率，并返回时有非对称的尖峰厚尾特征。于是，为了克服这些问题，并且作为GBM的扩充，我们考虑使用随机波动模型，使得波动的返回值是随机波动而且是由快速均值过程驱动。本文首先建立随机波动下的双障碍期权定价问题的模型，进而推导出了关于期权价格的偏微分方程。为下一步作出价格逼近、并进行数值计算奠定基础。

首先，令St为基础资产价值，σt为由Ornstein–Uhlenbeck(OU)过程Yt导出的随机波动过程，其中Yt服从均值m、方差v2的高斯分布。于是，关于St和Yt的随机微分方程为

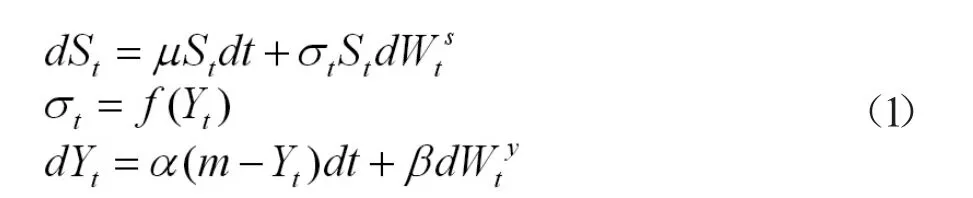
于是，为建立在风险中性概率测度P*下的新的动态模型，可知新的布朗运动如下描述：

其中γ(y)为波动风险的市场价格，是一个关于y的有界的光滑函数。根据Girsanov定理，均为测度 P*下的标准布朗运动，其中((μ-r)/f(Yt),γ(Yt))满足Novikov条件。因此，在P*下，模型（1）可化为下述随机微分方程

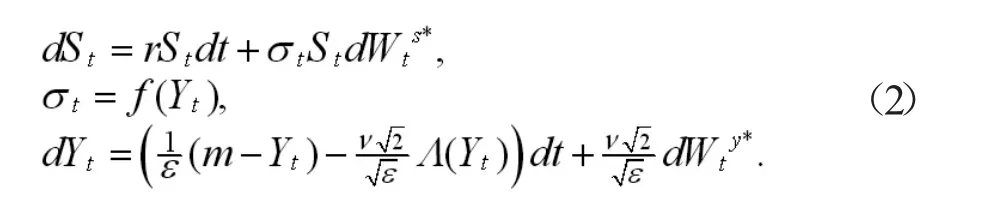
其中 L0，L1，L2定义如下：

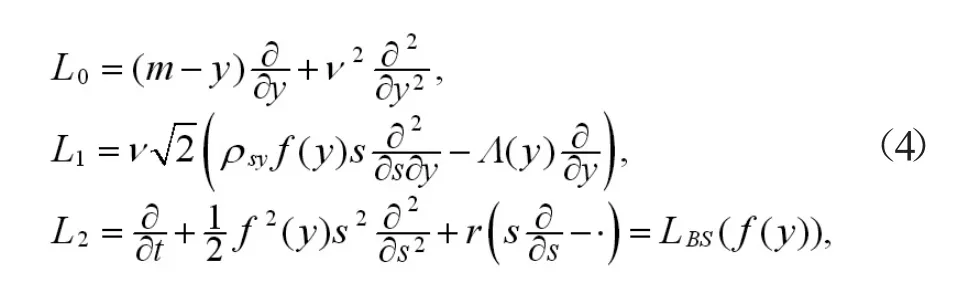
这里算子L0定义了过程Yt的市场概率测度的无穷小算子，仅作用于变量y；算子L1由两部分组成：第一部分是与两个布朗运动有关的混合偏微分算子，第二部分是市场价格波动风险下关于y的一阶偏微分算子；算子L2表示双障碍期权的Black Scholes算子。另外，（4）式中的 LBS即为 Black Scholes算子。

障碍期权的出现给那些金融风险管理者们提供了更合算的方法,让他们不必为他们认为不可能到达的价格支付费用了。同时为期权定价问题提供了一种新的解决思路。

[1]D Rich.The mathematical foundations of barrier option pricing theory.Adv.Futures Oper.Res.,7(1994)267-311.

[2]M Rubinstein,E Reine.Breaking down the barriers.Risk Mag.,4(8)(1991)28-35.

1004-7026（2017）09-0122-02

O211.6

A

DOI：10.16675/j.cnki.cn14-1065/f.2017.09.075

本文系2017年河北省社科基金项目（项目编号：HB17YJ094）系列论文。