浅谈分部积分列表法的用法

□杨 柳

（陕西国际商贸学院 陕西 咸阳 712046）

浅谈分部积分列表法的用法

□杨 柳

（陕西国际商贸学院 陕西 咸阳 712046）

分部积分是针对被积函数是乘积形式的积分，分部积分公式运用比较灵活。本文就列表的方法对分部积分加以说明，并列举列表法适用的类型。

分部积分；乘积列表法；函数

常见的积分方法有直接积分法，换元积分法，分部积分法。在被积函数是乘积形式的积分时，如果不能直接积分或者换元积分，那么一般会用到分部积分。分部积分公式∫udv=uv-∫vdu。分部积分前提是要选取恰当的u和v'函数，利用分部积分公式得到最后的结果，选取u和v'的方法比较固定，按照“反、对、幂、指、三”的顺序依次选择，两个函数乘积的积分，顺序靠左的函数是u，顺序靠右的函数是v'，指数函数和三角函数乘积中，u和v'函数的选取方式任意。或者有的教材中对被积函数分类，然后直接说明每一类中u和v'函数的选取。

1 列表法的计算规则

分布函数列表法是把被积函数分为两部分，分上下位置放置，上边是被积函数中能够求导，且越来越简单的函数，或者多次导数之后结果是0的函数[1]；下边放置的是被积函数的另外一部分，依次对其积分，积分次数与上面的导数次数相同即可。一般地，对积分∫f(x)g(x)dx，如果函数f(x)经过多次求导，结果等于0，或者结果是f(x)，可以用如下计算方法：

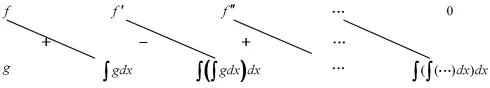
对f(x)函数多次求导，对g(x)函数多次积分，然后依次用斜线连接上下两行的函数，该项的符号由左向右依次为正负相间隔，然后写出积分关系式，得到的结果中可以含有积分符号。

例1求不定积分∫(x3+3x)exdx.

解 被积函数可以看做两个函数的乘积，x3+3x可以多次求导，而ex可以多次积分，用列表法求不定积分。

因此不定积分

∫(x3+3x)exdx=(x3+3x)ex+(3x2+3)ex+6xex+6ex+C=x3ex+3x2ex+9xex+9ex+C

例2求不定积分∫e2xcosxdx.

解 被积函数是乘积形式，但是cosx与e2x都不能经过多次求导而结果是0，但是它们求导之后又会回到最初的形式，也可以用列表的方法。

在例1中，求导的结果最终是0，0和下面一行中的函数相乘的积分结果还是0，因此可以直接写出整个积分的结果；例2中cosx求导两次的时候，形式仍然是cosx，这时候得到的是一个关系式，左右两侧都含有不定积分，移项得到需要的结果[2]。

2 列表法适用的类型

1.适用于∫Pn(x)eαxdx，∫Pn(x)sinxdx，∫Pn(x)cosxdx，其中Pn(x)是n次多项式。在用列表法的时候，Pn(x)可以多次求导，直至导数等于零，而eαx,cosx,sinx都可以多次积分。

2.适用于∫Pn(x)1nxdx，∫Pn(x)αrcsinxdx，∫Pn(x)αrccosxdx，其中 1nx，αrcsinx，αrctanx 可以求导，而 Pn(x)可以多次积分。

3.适用于∫sinαxebxdx，∫cosαxebxdx，任意选取需要求导的函数，求导两次之后的形式与最初相同，这时候得到关于积分的一个关系式，移项整理后就可以得到不定积分的结果，不定积分后需加常数C。

使用列表法的时候，具体要算到哪一步，根据情况而定。

3 列表法的评价

列表法的优点是:只针对函数乘积中的某一个函数多次求导或积分，消除了在应用分部积分时，既有积分又有求导的弊端。

列表法也有它的缺点：列表法有一定的局限性，对于特定的类型能取到较好的效果。但是如反三角函数与指数函数的乘积，就不能使用列表法。

[1]钱吉林.数学分析题解精粹[M].湖北：湖北辞书出版社,2009.

[2]同济大学数学系.高等数学[M].北京：高等教育出版社，2014.

1004-7026（2017）09-0147-01

0172.2

A

DOI：10.16675/j.cnki.cn14-1065/f.2017.09.094