基于属性权重向量组的多属性决策方法

段传庆, 涂振坤

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 数学学院,安徽 合肥 230009)

基于属性权重向量组的多属性决策方法

段传庆1,2, 涂振坤2

(1.合肥工业大学 管理学院,安徽 合肥 230009; 2.合肥工业大学 数学学院,安徽 合肥 230009)

文章基于属性权重完全未知的直觉模糊多属性决策问题,提出了一种属性权重向量组的决策方法。该方法认为决策对象应具有独立的属性权重,结合熵与离差最大化,确定所有选项的属性权重,构成一个权重向量组,并通过理想解与选项之间的关联系数进行排序。最后,文章通过算例说明了该方法的可行性。

直觉模糊数;熵;向量组;关联系数

0 引 言

在传统模糊集[1]基础上,文献[2-3]提出了直觉模糊集的概念。由于直觉模糊集同时考虑到隶属度、非隶属和犹豫度3个方面的信息,因此它比传统模糊集在处理模糊性和不确定性问题方面具有更大的灵活性。

在模糊集理论的决策问题中,属性权重往往起着至关重要的作用。但在实际问题中,属性权重常常由于决策者缺少数据或对该数据不了解而具有不确定性。如何确定属性的权重是决策理论的热门话题。熵权法是一种客观赋权法,国内外学者已做过大量的相关模糊熵研究[4-9]。文献[10]用模糊熵来确定属性的权重,但模糊熵往往只注重信息本身的重要性，而忽略了信息间存在的联系。文献[11]用离差法确定属性的权重,但离差法只注重信息间的关系而忽略了信息本身的重要性。再者从实际经验看,由于决策对象具有一定的独立性,即使是不同决策对象的同种属性,其在事物中起到的作用也不同,因而赋予的权重也不应相同。文献[10-15]在讨论过程中对不同决策对象的同种属性取同一权重,这具有一定的不合理性。文献[11]对5种ERP软件进行评估,选取了软件技术水平、功能满足程度、系统性能、软件信誉和服务水平5个指标,最终文中将5种软件的评估指标权重取同一个值进行计算。但由于5种软件可能的侧重点不同,有的侧重技术水平,有的侧重系统性能,有的侧重服务水平等,显然相同的指标在不同软件中的作用是不会完全相同的。如果最终将不同软件的同一指标取相同的权重,对于最终的结果将有失公允,也背离了最初优选的初衷。鉴于此，为了既考虑到数据本身的重要性，又兼顾到数据间的联系,本文将从信息熵和离差最大化2个方面出发提出一种求属性权重的新方法。该方法同时考虑了不同决策对象的同种属性值,并赋予它们不同的权重,得到属性的权重向量组。最后通过选项与理想解的关联系数进行排序。

1 基本理论

定义1[3]设X为一个非空集合,A={〈x,μA(x),vA(x)〉|x∈X}为直觉模糊集,其中μA(x)和vA(x)分别表示X中的元素x属于X隶属度和非隶属度,μA(x),vA(x)∈[0,1]且0≤μA(x)+vA(x)≤1。

此外,πA(x)=1-μA(x)-vA(x),表示直觉模糊集X中的元素x属于X的犹豫度。

定义2[16]设A={〈xi,μA(xi),vA(xi)〉,xi∈X},X={x1,x2,…,xm},则称

为A的直觉模糊熵,其中πA(xi)=1-μA(xi)-vA(xi)。

性质1E(A)=0,当且仅当A∈P(X),即当且仅当A为经典集合时,其对应模糊熵最小。

性质2E(A)=1，当且仅当∀x∈X,πA(x)=1。

性质3E(A)=E(Ac),其中，Ac为A的补集

性质4 当隶属度与非隶属度差的绝对值不变时,直觉模糊熵随着犹豫度的增大而增大;在犹豫度不变时,随着隶属度与非隶属度差的绝对值减少而增大。

定义3[17]A、B为2个直觉模糊集,则

为测定直觉模糊集A、B之间的距离,考虑其满足条件:

(1) 0≤d(A,B)≤1。

(2)d(A,B)=0,当且仅当A=B。

(3)d(A,B)=d(B,A)。

(4) 当A⊆B⊆C时,d(A,C)≥max(d(A,B),d(B,C))。

定义4[10]A、B为2个直觉模糊集,定义A、B的关联系数为:

(1)

A、B的信息直觉能为：

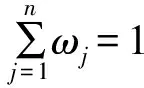
(2)

容易证明上述关联系数满足以下性质:① 0≤ρi(A*,Ai)≤1;②ρi(A*,Ai)=ρi(Ai,A*);③ 若A*=Ai，则ρi(A*,Ai)=1。

2 决策方法

决策者对于方案Ai关于属性Gj进行测度,属性值为直觉模糊数(μij,vij),i=1,2,…,m;j=1,2,…,n。从而构成直觉模糊决策矩阵R=(rij)mn=(μij,vij)mn。

由此可见,理想解中的每一项均为选项中各属性的最大值,理想解A*也即为各个选项中的最优解。且理想解中的数据均来自信息表本身,该理想解更符合自身的实际意义,计算结果也更具有说服力。

考虑到权重问题,(2)式可记为:

(3)

对于单个方案Ai的属性值Gj(j=1,2,…,n)，现有2种方法求其权重。

(4)

(2) 对于方案Ai,其某个属性与其他属性差别越大,则其发挥的作用越大,应赋予较大的权重,反之亦然。换句话说,方案Ai关于属性Gj的属性值rij与其他属性值间离差越大,则应赋予较大权重,因此方案Ai关于属性Gj的权重为:

(5)

如果将方法(1)和方法(2)综合考虑,既考虑数据本身重要性,又要注重数据间的联系,那么结合(4)式和(5)式给出方案Ai关于属性Gj的综合权重为:

(6)

(7)

由此得到方案Ai关于属性Gj的权重向量组(ωi1,ωi2,…,ωin)T,i=1,2,…,m,分别计算Ai与理想解A*的关联系数Si=ρ(Ai,A*),i=1,2,…,m。对Si进行排序,Si越大Ai越优。

综上所述,给出如下算法:

(1) 设方案Ai在属性Gj下的属性值为rij,于是得到直觉模糊决策矩阵。

(2) 由(7)式可求出属性权重ωij,其中i=1,2,…,m;j=1,2,…,n。得到Ai关于属性Gj的权重向量组(ωi1,ωi2,…,ωin)T,i=1,2,…,m。

对Si进行排序,Si越大说明Ai越优。

3 算例分析

取文献[16]的部分数据。某公司准备提拔一名部门经理,现有5名候选人A=(A1,A2,A3,A4,A5)符合提拔条件。公司分别从G=(G1,G2,G3,G4,G5,G6)6个方面进行评估,并将结果以直觉模糊信息形式给出,具体见表1所列。

表1 某公司提拔一名部门经理直觉模糊信息

利用(7)式分别求出选项Ai关于属性Gj的权重向量组如下：

ω1=(0.192 3,0.167 3,0.182 8,134 0,

0.156 3,0.167 3)T，

ω2=(0.151 2,0.174 6,0.197 1,0.163 6,

0.163 6,0.149 9)T，

ω3=(0.204 1,0.174 0,0.141 5,0.141 5,

0.207 6,0.131 3)T，

ω4=(0.211 8,0.195 9,0.169 0,0.125 3,

0.165 4,0.132 6)T，

ω5=(0.157 4,0.165 1,0.145 3,0.175 9,

0.182 5,0.173 8)T。

记理想解为A*,利用(3)式得到:

由此可见，排序为：A3>A4>A1>A5>A2，与原文排序相同。

4 结 论

本文研究了属性权重完全未知的直觉模糊多属性决策问题。从实际经验看,事物具有一定的相对独立性,即使是不同事物的相同属性，其权重也不应相同。基于上述思想,本文认为不同决策对象的相同属性应该具有不同的权重,同时考虑到信息本身和信息之间的重要性，提出了结合信息熵与离差最大化来确定各选项的属性权重向量组的新方法。该方法假定决策对象本身模糊性与事物间的联系具有同等重要性,通过平衡因子t来调节两者的关系。但是在有些情况下,决策对象本身的模糊性与决策对象间的联系重要程度不一致,因此正确选择平衡因子t将是进一步深入研究的方向。本文最后通过算例说明了该方法的可行性。

[1] ZADEH L A.Fuzzy set[J].Information and Control,1965,8(3):338-356.

[2] ATANASSOV K.Intuitionistic fuzzy sets[J].Fuzzy Sets and systems,1986,20(1):87-96.

[3] ATANASSOV K.More on ituitionistic fuzzy sets[J].Fuzzy Sets and Systems,1989,33(1):37-45.

[4] MAO Junjun,YAO Dengbao,WANG Cuicui. A novel crossentropy and Entropy measures of IFSs and their applications[J].Knoledge-Bas-ed Systems,2013,48:37-45.

[5] 王晓杰,魏翠萍,郭婷婷.基于交叉熵和熵的直觉模糊多属性群决策专家权重的确定[J].曲阜师范大学学报(自然科学版),2011,37(3):35-40.

[6] 赵萌,任嵘嵘.基于模糊熵的直觉模糊多属性群决策方法[J].数学的实践与认识,2014,44(23):153-159.

[7] 戚晓雯,梁昌勇,张恩桥,等.基于熵最大化的区间直觉模糊多属性群决策方法[J].系统工程理论与实践,2011,31(10):1940-1948.

[8] 陈晓红.基于熵和关联系数的区间直觉模糊决策方法[J].系统工程与电子技术,2013,35(4):791-794.

[9] 李兰平.基于一类新的直觉模糊熵的直觉模糊多属性决策法[J].齐齐哈尔大学学报,2014,30(2):83-86.

[10] JUN Y.Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment[J].Europen Journal of Operational Research,2010,205:202-204.

[11] 梁昌勇,戚筱雯，丁勇，等.一种直觉模糊多属性群决策方法及其在群决策中的应用[J].运筹与管理,2013,22(1):41-47.

[12] 李宝萍,陈华友.一类基于交叉熵的区间直觉模糊多属性群决策的新方法[J].统计与决策,2014(1):20-23.

[13] 张英俊,马培军，苏小红，等.属性权重不确定条件下的区间直觉模糊多属性决策[J].自动化学报,2012,38(2):220-227.

[14] ZHANG Q S,LIU F C,WU L H,et al. Information entropy,similarity measure and inclusion measure of intuitionistic fuzzy sets[C]//International Conference on Information Computing and Applications,2012:392-398.

[15] 南疆霞,李登峰,张茂军.直觉模糊多属性决策的TOPSIS法[J].运筹与管理,2008,17(3):34-47.

[16] 王翠翠,姚登宝,毛军军，等.基于熵和关联系数的直觉模糊多属性决策方法[J].计算机应用,2012,32(11):3002-3004.

[17] HONG D H,KIM C.A note on similarity measures between vague sets and between elements[J].Information Science,1999,115(4):83-96.

(责任编辑 万伦来)

Approach to multi-attribute decision making based on vector group of attribute weights

DUAN Chuanqing1,2， TU Zhenkun2

(1.School of Management, Hefei University of Technology, Hefei 230009, China; 2.School of Mathematics, Hefei University of Technology, Hefei 230009, China)

This paper proposes an approach to multi-attribute decision making based on vector group of attribute weights with unknown attribute weights information where individual assessments are provided as intuitionistic fuzzy numbers. In this approach, it is considered that the decision objects have independent attribute weights. To gain the attribute weights, a new method is proposed based on the entropy and maximizing deviations. Then the vector group of attribute weights is gotten. And a method for ranking the alternatives by correlation coefficient is proposed. Finally, an example is given to illustrate the effectiveness of the method.

intuitionistic fuzzy number; entropy; vector group; correlation coefficient

2016-03-08；

2016-07-30

中央高校基本科研业务费专项资金资助项目(J2014HGXJ0080;JZ2016HGBZ0809)

段传庆(1978-),男,安徽淮南人,博士,合肥工业大学讲师.

10.3969/j.issn.1003-5060.2017.05.026

C934

A

1003-5060(2017)05-0708-04