基于移动有限元法的裂纹梁振动分析

梁岗 曹沛 唐炯 沈晴 李心爽

(1.上海海事大学物流工程学院, 上海 201306) (2.上海振华重工(集团)股份有限公司, 上海 200125)(3.美国康涅狄格大学机械工程系, 美国)

基于移动有限元法的裂纹梁振动分析

梁岗1曹沛2†唐炯3沈晴2李心爽2

(1.上海海事大学物流工程学院, 上海 201306) (2.上海振华重工(集团)股份有限公司, 上海 200125)(3.美国康涅狄格大学机械工程系, 美国)

采用移动有限元法和局部柔度法对移动质量作用下含裂纹简支梁进行了振动计算分析.计算考虑了裂纹和移动质量的相对位置对梁固有频率的影响,以及移动质量在不同位置、速度情况下对裂纹梁的动力响应的影响.结果分析表明,裂纹与移动质量的存在会使得梁的动态位移有不同程度的增大,且随着移动质量位置和裂纹位置的改变会使得梁的固有频率变小.

移动有限元, 简支梁, 张开裂纹, 固有频率, 动力响应

引言

移动载荷对梁结构动力特性的影响在港口起重运输机械上是一个很重要的课题,如桥式起重机载重运行和岸边集装箱起重机装卸作业等均可简化为移动质量-梁耦合系统.目前,工程实践中常以梁的固有频率代替移动质量-梁的耦合频率,但是考虑到移动质量在运动过程中,质量-梁组成的系统会产生耦合振动,对梁的固有频率产生较大影响；另外,由于各种因素的影响,梁结构中极易产生微观裂纹.裂纹的存在不仅改变了裂纹尖端区域应力场,而且改变了梁结构动力特性.这些微观裂纹若不及时发现、处理,其失稳扩展而引起的断裂,将导致整个梁结构产生毁灭性的破坏.故本文将针对移动质量-梁系统分析不同程度裂纹梁的振动特性,对更加准确地获得梁结构的固有频率、保证梁结构安全可靠具有重要意义.

对于移动质量-梁模型的研究,在过去的十几年里研究人员在系统建模、动力学分析方面已经有许多研究成果[1-10],其中Wayou[7]研究了欧拉-伯努利梁在移动力下的非线性动态分析,彭献[8-9]分析了移动质量作用下梁固有频率的变化,Ismail Gerdemeli[10]利用移动有限元法研究了随着移动质量大小的变化对梁固有频率的影响.

如何有效地识别和检测裂纹具有十分重要的工程意义[11].对此,国内外学者应用不同的方法对有关裂纹梁的动力特性问题进行了深入研究,从解析解、半解析解到数值方面的计算都提出了一系列的解决方案[13-20].而基于振动特性的裂纹检测法作为一种无损检测的方法近年来越来越受到重视[12].

本文基于移动有限元法,根据移动质量-梁系统的动力学方程,建立了Euler-Bernoulli梁与移动质量耦合单元的时变质量、刚度、阻尼矩阵.并利用卡式定理导出含裂纹梁单元的柔度矩阵,基于力平衡条件导出裂纹梁单元的刚度矩阵.在此基础上,以堆场内集装箱起重机为例,计算了移动质量作用下含裂纹简支梁的动态特性及动力响应,并对结果进行了对比分析.对集装箱起重机的动态设计、动力性能评估以及振动的控制具有一定的指导意义.

1 裂纹梁振动的移动有限元法

如图1所示,将梁分为若干个单元,移动质量mp以恒定的速度vm沿梁运动,其中第S个单元含有移动质量,第K个单元含有裂纹,考虑移动惯性载荷作用下的系统运动方程为：

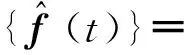
(1)

图1 移动质量下含有裂纹的简支梁Fig. 1 Simple support crack beam due to a moving mass

1.1 移动有限元原理

图2为一载有移动质量mp的梁单元,单元有两个节点,每个节点有两个自由度.移动质量在梁上的位置随着时间的变化而变化.

图2 含有移动质量的梁单元Fig. 2 Beam element with moving mass

当梁在振动时,梁在移动质量下的所受的横向力为[3]：

(2)

其中：

(3)

fy(x,t)是移动质量在t时刻,x位置处作用的力.δ(x-xp)为狄拉克函数,g为重力加速度.x0和v0是初始位置和初始速度.

考虑移动质量的惯性影响,梁的横向加速度方程可以写为[19]：

(4)

当质量块匀速运动时,(4)式可以写为：

(5)

(5)式的另外一种形式为：

(6)

其中：“ .”为对时间的导数,“ ′”为对位移的导数,wy=wy(x,t)是梁的纵向挠度关于时间和位移的函数.将(6)带入(2)中,得：

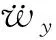
(7)

在质量块匀速移动下,单元的等效节点力为：

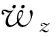
(8)

Ni(i=1～4)为梁单元的形函数：

N1=1-3ξ(t)2+2ξ(t)3

N2=[ξ(t)-2ξ(t)2+ξ(t)3]l

N3=3ξ(t)2-2ξ(t)3

N4=[-ξ(t)2+ξ(t)3]l

(9)

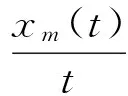
形函数和位移、时间之间的关系为：

wy(x,t)=N1us1+N2us2+N3us3+N4us4

(10)

其中,usi(i=1～4)为单元的节点位移.

将(10)带入(8),并将所得表达式写为矩阵形式：

(11)

其中,

(12e)

(12f)

(12g)

[m]、[c]、[k]为移动有限元的时变质量、阻尼和刚度矩阵.移动质量的位置xp(t)与质量和速度有关.

1.2 裂纹梁单元

利用局部柔度理论建立裂纹梁单元的有限元模型.对于一个含有裂纹的欧拉-伯努利梁单元.单元长度为l,相对于梁单元的左端裂纹位置为l1.应用局部能量法来推导裂纹梁单元的刚度矩阵[20].

对于无裂纹梁单元的应变能为：

(13)

其中：E为杨氏模量,I为截面的惯性矩,l为梁单元的长度.梁单元的弯矩方程可以写为：

Mb=Tl+M

(14)

其中：T为单元所受的剪力,M为单元的弯矩.

由于裂纹的存在,裂纹梁单元相对于一般的梁单元存在附加的应变能,根据Tada[17]的理论：

(15)

其中：A为梁单元的横截面积,μ为泊松比,KⅠ、KⅡ、KⅢ为应力强度因子.

图3 裂纹梁单元Fig. 3 Cracked beam element

根据无裂纹梁理论,无裂纹梁单元的弹性系数可以写为：

(16)

而考虑裂纹梁的附加应变能,其弹性系数为：

(17)

对于一个裂纹梁单元,单元的平衡方程可以写为：

(18)

根据公式(13)(14)和(15)～(17)弹性矩阵[C]可以写为：

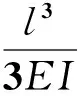
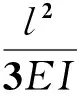
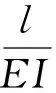
(19)

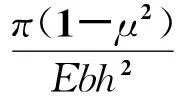
根据公式(19),裂纹梁的刚度矩阵可以写为：

(20)

2 系统动力方程求解

由图1所示的多自由度系统的振动方程为：

(21)

(22)

(23)

除了含有移动质量的S单元和含有裂纹的K单元：

(24)

(25)

(26)

(27)

随时间变化的xm(t)和S可由(28)(29)得来：

xm(t)=xp(t)-(s-1)l

(28)

(29)

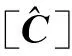
(30)

对于公式(21)所给出的动力方程,可以通过Newmark数值积分来得出结果.

3 数值结果

本文给出的所有结果,是在重力加速度为9.81m/s2、阻尼率为ξ1=ξ2=0.05对应于以前两阶固有频率ω1,ω2；取m为移动质量的大小,M为梁的质量.取梁的参数为：高h=0.5m,宽b=1m,长L=30m.简支梁的材料属性：密度7890kg/m3、杨氏模量2.01×1011Pa、泊松比0.3.

3.1 移动质量下裂纹梁的固有频率

为了揭示耦合系统各阶频率随移动质量与梁的质量比、位置比和裂纹相对位置的变化规律,按特征值计算法的结果,绘出该耦合系统的前三阶固有频率随裂纹位置比β和系统质量位置比λ变化的三维图形分别如图4、图5、图6所示.

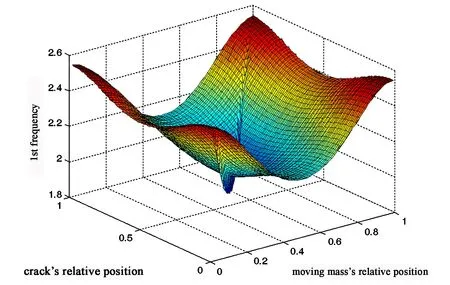
图4 耦合系统的第一阶固有频率随λ和β变化的三维图Fig. 4 3-dimension graph of 1st natural frequency of the coupled system with the change of λ and β

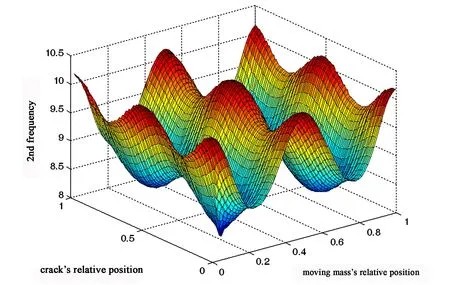
图5 耦合系统的第二阶固有频率随λ和β变化的三维图Fig. 5 3-dimension graph of 2nd natural frequency of the coupled system with the change of λ and β

图6 耦合系统的第三阶固有频率随λ和β变化的三维图Fig. 6 3-dimension graph of 3rd natural frequency of the coupled system with the change of λ and β

假定当相对裂纹深度为0.5，质量比为:m/M=0.2时.由以下三图可以清晰地看到,移动质量与简支梁耦合系统的各阶固有频率随裂纹位置比和质量位置比呈简谐函数规律变化,一阶为半波,二阶为全波,三阶为1.5倍全波,且阶数愈高波数越高.且根据图像数据可以计算出,第一阶频率的变化范围为0～25.49%；第二阶频率的变化范围为0～17.31%；第三阶频率的变化范围为0～14.71%.且当裂纹位置和移动质量位置重合时的固有频率相对于其他位置时会有较为显著的下降.

综上所述,移动质量与裂纹梁耦合系统的各阶固有频率并非常数,而与系统的质量比、位置比和裂纹相对深度、相对位置有关；若用梁的固有频率代替耦合系统的固有频率有时会产生较大的误差.

3.2 移动质量下裂纹梁的动态响应

利用上述理论编写程序,将简支梁分为50个单元.取裂纹相对深度为0.5,相对位置为0.5,移动质量与梁的质量比为：m/M=0.2.

图7为移动质量在不同速度时,梁跨中处的动态响应.当移动质量在裂纹梁上运行时,梁的挠度相比于无损梁的挠度加大.并且在同一移动速度下,裂纹梁跨中处达到最大挠度的时刻要比无损梁达到最大挠度的时刻推后.并且随着速度的增加,裂纹梁跨中处达到最大挠度的时刻有着向后推移的趋势.当v=4m/s时,移动力与移动质量的计算误差为6.4%；当v=10m/s时,移动力与移动质量的计算误差为18.5%.表明随着速度的增加,移动质量惯性力对梁动态响应的影响增加.

图7 动质量在不同速度作用下裂纹梁的动态响应(裂纹相对深度α=0.5；相对位置β=0.5)(--移动力无裂纹, —○—移动力有裂纹—移动质量无裂纹,—●—移动质量有裂纹)Fig. 7 Dynamic response due to moving mass in different velocity

图8表明裂纹对梁在不同时刻振动形状的影响(v=10m/s、m/M=0.4).当移动质量接近梁的右端时,裂纹对梁振动的影响越来越小.随着质量比和速度的增加,裂纹对梁挠屈变形影响最大的时刻并不是质量移动到裂纹位置时(裂纹相对位置为0.5),而是在t/T=0.6左右.

图8 移动质量在速度为10m/s时,裂纹梁和无裂纹梁在七个时刻的形状Fig. 8 Beam shape for v=10m/s, α=0.5,mid-span

图9所示为裂纹程度的加深对梁跨中处动态响应的影响(v=10m/s、m/M=0.4).随着裂纹程度的增加跨中处动态响应的最大位移增大,当裂纹相对深度α=0.2为时,跨中处最大挠度值较无损梁下降了0.16%；当α=0.3时,跨中处最大挠度值较无损梁下降了0.64%；当α=0.4时,跨中处最大挠度值较无损梁下降了3.23%；当α=0.5时,跨中处最大挠度值较无损梁下降了13.09%.表明随着裂纹相对深度的增加,裂纹对梁跨中处的动态响应越敏感.

图9 裂纹深度的变化对动态响应的影响Fig. 9 Effect of crack size on the time response at mid-span

4 结论

本文利用移动有限元和裂纹梁单元理论对移动质量下简支裂纹梁进行动力学计算分析,得出移动质量作用下裂纹的存在相比于无损梁会产生更大的动态挠屈变形.运用移动有限元法,考虑移动质量的惯性力对梁结构动态性能的影响,随着动载速度的增加,相比于移动力,惯性力对梁动态特性的影响更显著,且惯性力对裂纹的影响使得梁跨中处达到最大挠度的时刻向后偏置.当裂纹相对深度达到α=0.5时,梁的动态挠度会有显著的增大,若不及时发现处理将会导致结构的破坏.

1 李海斌,毕世华,方远乔. 运动刚体激励下弹性梁的振动响应分析. 工程力学, 1998,15(4):74～80 (Li H B, Bi S H. Fang Y Q. Vibraction analysis of beams activated by moving rigid body.EngineeringMechanics, 1998,15(4):74～80 (in Chinese))

2 M.A.M Ahmoud, M.A.A Bou, Z Aid. Dynamic response of a beam with a cracksubject to a moving mass.JournalofSoundandVibration, 2002,256(4):591～603

3 Cifuentes A O. Dynamic response of a beam excited by a moving mass.FiniteElementsinAnalysisandDesign, 1989,5:237～246

4 Wu J J, Whittaker A R, Cartmell M P. The use of finite element techniques for calculating the dynamic response of structures to moving loads.ComputersandStructures, 2000:78:789～799

5 Foda M A, Abduljabbar Z. A dynamic Green's function formulation for the response of a beam structure to a moving mass.JournalofSoundandVibration, 1998,210(3):295～3066 Zhu X Q, Law S S. Precise time-step integration for the dynamic response of acontinuous beam under moving loads.JournalofSoundandVibration, 2001,240(5):962～970

7 Wayou A N Y, Tchoukuegno R, Woafo P. Non-linear dynamics of an elastic beam under moving loads.JournalofSoundandVibration, 2004,273:1101～1108

8 彭献,游福贺. 移动质量与梁耦合系统固有频率的计算与分析. 动力学与控制学报, 2009,7(3):270～274 (Peng X, You F H. Calculation and analysis on natural frequency of a moving mass and beam′s coupled system.JournalofDynamicsandControl, 2009,7(3):270～274(in Chinese))

9 彭献,殷新锋. 车-桥系统的振动分析及控制. 动力学与控制学报, 2006,4(3):253～258 (Peng X, Yin X F. Vibration analysis and control on vehicle-bridge system.JournalofDynamicsandControl, 2006,4(3):253～258)

10Ismail Gerdemeli, Ismail Esen, DeryaÖzer. Dynamic response of an overhead crane beam due to a moving mass using moving finite element approximation.KeyEngineeringMaterials, 2011,450:99～102

11范天佑. 断裂理论基础. 北京：科学出版社, 2003 (Fan T Y. Theoretical basis of fracture. Beijing: Press of Science, 2003 (in Chinese))

12吴宁祥,谢里阳,吴克勤,由美雁. 裂纹梁动力学仿真的有限元模型. 东北大学学报, 2008,29(5):714～717 (Wu N X, Xie L Y, Wu K Q, You M Y. An improved finite element model for dynamic simulation ofcracked beam.JournalofNortheasternUniversity, 2008,29(5)714～717(in Chinese))

13刘文光,陈国平. 呼吸式裂纹梁的振动疲劳裂纹扩展耦合分析. 中国机械工程, 2010,21(23):2798～2802 (Liu W G, Chen G P.Coupling analysis of vibration fatigue crack growth for breathing cracked beam.MechanicalEngineeringofChina, 2010,21(23):2798～2802(in Chinese))14李兆军,龙慧,刘洋,邱旻. 基于有限元位移模式的含裂纹梁结构动力学模型. 中国机械工程, 2014,25(12):1563～1566 (Li Z J, Long H,Liu Y, Qiu H. Dynamics equation of cracked beam based on finite element displacement mode.MechanicalEngineeringofChina,2014,25(12):1563～1566(in Chinese))

15吴宁祥,谢里阳,吴克勤等. 裂纹梁的相似特性及模型误差分析. 机械强度, 2006,28(4):570～573 (Wu N X, Xie L Y, Wu K Q, et al. Similarity of cracked beam and model error analysis.MechanicalStrength, 2006,28(4):570～573 (in Chinese))

16钱管良,顾松年,姜节胜. 含裂纹梁的动力响应. 振动工程学报, 1989,2(3):78～85 (Qian G K, Gu S N, Jiang J S. The dynamic response of beam with crack.JournalofVibrationEngineering, 1989,2(3):78～85 (in Chinese))

17Tada H, Paris P, Irwin G. The stress analysis of cracks handbook. Hellertown, PA: Del Research Corp, 1973

18Clough R W, Penzien J. Dynamics of structures 3rd ed. Computers and Structures, Inc., Berkeley, 2003

19Fryba L. Vibration solids and structures under moving loads, Thomas TelfordHouse, London, 1999

20Nahvi H . Crack detection in beams using experimental modal data and finite element model. Mechanical Science, 2000

† Corresponding author E-mail:dick77891@qq.com

23 January 2016,revised 10 October 2016.

VIBRATION ANALYSIS OF A CRACKED BEAM BASES ON MOVING FINITE ELEMENT APPROACH*

Liang Gang1†Cao Pei1Tang Jiong2Shen Qing2,Li Xinshuang2

(1.CollegeofLogisticsEngineering,ShanghaiMaritimeUniversity,Shanghai201399,China)(2.ShanghaiZhenhuaHeavyIndustryCoLtd,Shanghai200125,China)(3.DepartmentofMechanicalEngineering,UniversityofConnecticut,American)

The vibration of a cracked beam due to a moving mass is investigated by using the moving finite element method and the local flexibility method. The effect of the relative position and relative depth of the crack on the natural frequency and the dynamic response of the cracked beam under different velocity are discussed through the numerical calculation. The analysis shows that the crack and the moving mass increase the dynamic displacement of beam, but decrease the coupling frequency of the system in a certain degree. Meanwhile, with the increase of the speed of moving mass and the relative depth of crack, the dynamic response of the beam is apt to increase.

moving finite element, simple support beam, open crack, natural frequency, dynamic response

10.6052/1672-6553-2016-051

2016-01-23收到第1稿,2016-10-10收到修改稿.

† 通讯作者 E-mail:dick77891@qq.com