关于非完整系统的Ценов方程和Mac Millan方程*
李彦敏 梅凤翔 吴惠彬
(1.商丘师范学院物理与电气信息学院,商丘 476000) (2.北京理工大学宇航学院,北京 100081)(3.北京理工大学数学学院,北京 100081)
关于非完整系统的Ценов方程和Mac Millan方程*
李彦敏1†梅凤翔2吴惠彬3
(1.商丘师范学院物理与电气信息学院,商丘 476000) (2.北京理工大学宇航学院,北京 100081)(3.北京理工大学数学学院,北京 100081)
Ценов方程和Mac Millan方程是非完整力学史上较晚出现的运动方程.这些方程的建立不仅有历史意义,而且有理论和应用的优势.本文对Ценов方程和Mac Millan方程的形成提供一些史料,并提出一些看法.
分析力学, Ценов方程, Mac Millan方程, 形成史
引言
Ценов N(1883-1967)是保加利亚著名数学家、科学院院士.Mac Millan WD(1871-1948)是美国著名天文学家和数学家.他们在非完整力学方面的贡献主要是他们各自得到的非完整系统的新型运动方程.本文就分析力学的Ценов方程和Mac Millan方程的形成和发展给出一些史料.史鉴使人明智,这也是让大家了解学科史的宗旨.
1 Ценов 方程
1.1 Ценов 简介
Иван Ценов Ангелов(1883-1967),汉译伊力·采诺夫·安格洛夫,英译I. Tsenov,法译I. Tzénoff,保加利亚著名数学家.按习惯他应叫И. Ангелов,但他自己取名И. Ценов.生于1883年1月2日,卒于1967年9月19日.1929年成为保加利亚科学院院士,1951年获季米特洛夫奖金,1965年被誉为人民科学活动家.1922-1951年任索菲亚大学教授和分析力学教研室主任,1951-1958年为一般和应用数学教研室主任.采诺夫有不少关于分析力学的论著,有“采诺夫方程”等.
1.2 混合型方程(1924)
对非完整约束系统,将系统的加速度能S分成两部分,一部分S0仅含独立的广义加速度,另一部分S1仅含不独立的广义加速度,结果运动方程一部分是Euler-Lagrange型的,另一部分是Appell型的.
设非完整约束是双面理想的,有形式:
(σ=1,2,…,ε; ε=n-g; β=1,2,…,g;
s=1,2,…,n)
(1)
这儿及以后相同指标表示求和.将加速度能S表示为:
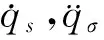
(2)
将式(1)对时间t求导数,得:
(3)
其中未写出之项不含广义加速度.令:
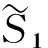
(4)
则方程有形式:
(5)
其中,
(6)
为嵌入约束后的广义力.
方程(5)就是Tzénoff 1924年导出的非完整系统的方程[1],它是由Euler-Lagrange型与Appell型混合而成的,称为混合型方程.这类方程对某些问题有可能兼顾Lagrange方程和Appell方程的优点.为叙述方便,将方程(5)称为第一类Tzénoff方程.
1.3 类Appell型方程(1953)
设系统的位型由n个广义坐标qs(s=1,2,…,n)来确定.Tzénoff构造一函数[2]:
(7)
其,T为系统动能,Qs为广义力,而:
(8)
Gauss原理成为:
(9)

(10)
这就是Tzénoff 在1953年导出的方程,它与Appell方程类似,故称为类Appell型方程,也可称为第二类Tzénoff方程.
1.4 Tzénoff工作的推广与发展
1.4.1 万有d′Alembert原理
罗马尼亚学者Mangeron和Deleanu的万有d′Alembert原理[3]:
(11)
在广义坐标下可写成以下形式:
(12)
1.4.2 广义Tzénoff函数
保加利亚学者Dolaptchiew(Далапчиев)于1966年给出广义Tzénoff函数[4]为:
(13)
当m=2时,它为Tzénoff函数(7).
1.4.3 第一类Tzénoff方程的推广
Dobronravov指出[5],混合型方程(5)表面复杂,但实际应用中会有方便之处.Dobronravov的这本专著是梅凤翔在法国进修时(1981.01-1982.12),他的导师Pironneau(1923-1983)教授跟Rumyantsev(1921-2007)院士要来的,梅凤翔复印了全书.
1.4.4 第二类Tzénoff方程的推广
Dobronravov称方程(10)为二阶Tzénoff方程[5].文献[6-14]将第二类Tzénoff方程做了各种推广,文献[15]还研究了方程的对称性与守恒量.
1.5 小结
19世纪末至20世纪初是非完整力学的奠基时期,这个时期Chaplygin(1869-1942),Voronetz(1871-1923),Volterra(1860-1940),Appell(1855-1930),Hamel(1877-1954)等的工作为非完整力学奠定了基础,出现了各类运动微分方程.但是,运动微分方程的研究并未停止,其中,Tzénoff 在1924年和1953年的工作都很重要,后人对他工作的推广足以证明这一点.力学史著作[16]提到Tzénoff的工作,并认为Tzénoff发展了Voronetz的工作.
2 Mac Millan方程
2.1 Mac Millan简介
MacMillan WD(1871-1948),汉译麦克米伦,美国天文学家、数学家.生于威斯康星州的拉克罗斯,卒于明尼苏达州的圣保罗.曾在弗吉尼亚大学福雷斯特湖学院和沃恩堡大学学习,1898年在沃恩堡大学获文学士学位.随后进芝加哥大学学习,1906年获硕士学位,1908年获哲学博士学位.1907-1908年为该校地质学的助理研究员,1908-1909年为数学和天文学的助理研究员,1936年为该校名誉教授.主要从事星原学以及应用数学中与此相关的课题研究.着重研究行星和恒星的形成,提出两个假设:宇宙保持于一种稳定状态和宇宙的一个大范围内的能量守恒.这些假设可以解释所谓德切斯库—奥尔佰斯佯谬以及宇宙射线的来源.对位势理论、具有周期系数的微分方程理论、自守函数理论均有开创性研究.对相对论在美国的传播也做出了贡献.著有《理论力学》(3卷,1927-1936)(摘自《科学家大词典》(上海:上海辞书出版社,上海科技教育出版社,2000)).
MacMillan的专著有:
Theoretical Mechanics,
Vol 1 The Statics and the Dynamics of a Particle(1927, reprinted 1958 by Dover, New York);
Vol 2 The Theory of the Potential(1930, reprinted 1958 by Dover);
Vol 3 Dynamics of Rigid Bodies(1936, reprinted 1960 by Dover).
(摘自 Papastravridis的《分析力学》[17]).
2.2 Mac Millan方程
1936年Mac Millan在他的《刚体动力学》第154节“Lagrange方程对非完整系统情形的推广”中给出如下方程[18]:
(14)
其中,

Wj=∑m(ξjx′+ηjy′+ζjz′)
方程(14)后人称为Mac Millan方程.
上式中的“一撇儿”表示对时间t的导数;T为用独立广义速度表示的动能;因为一开始就考虑到非完整约束,故ξj,ηj,ζj不为零;Wj为添加项,表示由非完整约束引起的特殊项;如果没有非完整约束,则Wj=0(j=1,2,…,n),方程成为Lagrange方程,因此,Mac Millan称其为Lagrange方程的推广.
2.3 Mac Millan方程的影响与发展
1)Mac Millan方程是非完整力学史上较晚出现的方程,比Appell方程晚37年,但仍受到学者们的关注.
2)周培源先生是最早认识到Mac Millan方程重要性的学者,在他的《理论力学》[19](1952)中介绍了这类方程,但没有提名字.
3)苏联著名非完整力学专家Dobronravov V V 1961年在莫斯科包曼工学院的《力学》上刊登论文“d′Alembert-Lagrange原理、Hölder原理和带非完整约束的力学系统的运动方程”,其中提到Mac Millan方程,并称其为“自然方程”[20].
Dobronravov的“自然方程”的提法很有道理,因为当没有非完整约束时,添加项Wj为零,Mac Millan方程就“自然地”成了Lagrange方程.
4)Dobronravov指出,Mac Millan方程不能推广到非线性非完整系统[20],但是这种论断是不对的[21],文献[22]做了这种推广.
设力学系统的位型由n个广义坐标qs(s=1,2,…,n)来确定,它的运动受有g个双面理想Chetaev型非线性非完整约束.
(β=1,2,…,g;s=1,2,…,n;σ=1,2,…,ε;
ε=n-g)
广义Mac Millan方程有形式[22]:
(15)
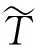

文献[23-25]将Mac Millan方程推广到变质量系统,文献[26-27]研究了准坐标下的Mac Millan方程,文献[28]研究了事件空间中的Mac Millan方程.
5)Mac Millan方程的优点在于它是“自然地”, “自然地”说明为什么第二类Lagrange方程不适用于非完整系统.这类方程的缺点在于它还没有脱离开直角坐标,因此,添加项Wj的计算比较繁琐.
6)Dobronravov曾提出,在由d′Alembert-Lagrange原理推导非完整系统的运动微分方程时何时考虑非完整约束的问题[29].他分成两类,一类是一开始就注意到非完整约束,如Appell,Volterra,Mac Millan等.另一类是将原理变换到广义坐标形成后才考虑非完整约束,如Chaplygin,Hamel等.由此可见,Mac Millan方程的历史地位.
2.4 小结
MacMillan对非完整力学的贡献主要是他在《理论力学》第三卷《刚体动力学》中导出的自然方程.他的这套书很有名,其中第三卷在1951年被译成俄文.
3 结语
Ценов的两类方程(1924,1953)和Mac Millan方程(1963)是非完整力学史上较晚出现的运动方程.这些方程不仅有它们的历史意义,而且有其理论和应用上的优势.本文介绍了这些方程的起源及其后学的发展.学习两位大学问家的创新精神,十分重要.
1 TzénoffⅠ. Sur les équations du mouvement des systèmes maténels non holonomes. Math. Annalen Leibzig, 1924,91:161~168
2 Ценов И. Об одной новой форме уравнений анал итической динамики. Доклад Академии Наук СССР, 1953,89(1):21~24
3 Mangeron D, Deleanw S. Sur ane classe d′équation de la mécanique analytique au sens de I. Tzénoff. Докл. Балг. АН, 1962,15(1):9~12
4 Doloptchiew B. Sur les systèmes mécaniques non holonomes assujettis à les liaisons arbitraires. C. R. Acad. Sc. Paris, 1966,262(1):31~34
5 Добронравов ВВ. Основы Механики Неголомных Сисгем. Москва: Высшая Шкала, 1970
6 梅凤翔,刘端,罗勇. 高等分析力学. 北京: 北京理工大学出版社, 1991 (Mei F X, Liu D, Luo Y. Advanced analytical mechanics. Beijing: Beijing Institute of Technology Press, 1991(in Chinese))
7 薛问西. Appell方程Tzénoff方程的推广. 力学学报, 1987,19(2):156~164 (Xue W X. Generalization of Appell equation and Tzénoff equation.ActaMechanicaSinica, 1987,19(2):156~164 (in Chinese))
8 程丁龙. Ценов方程对变质量非完整系统的推广. 北京工业学院学报, 1987,7(3):76~85 (Cheng D L. Generalization of Ценов equation to variable mass nonholonomic systems.JournalofBeijingUniversityofTechnology, 1987,7(3):76~85 (in Chinese))
9 梅凤翔. 事件空间中非完整保守系统的广义Ценов方程. 兵工学报, 1988,4(4):27~85 (Mei F X. Generalized Ценов equation of non-holonomic conservative systems in the event space.ActaArmamentarii, 1988,4(4):27~85 (in Chinese))
10罗绍凯. 非线性非完整系统的相对论性Ценов方程及其正则形式. 洛阳工学院学报, 1990,11(1):93~97 (Luo S K. Relativistic Ценов equation of nonlinear nonholonomic mechanical systems and its canonical form.JournalofLuoyangInstituteofTechnology, 1990,11(1):93~97 (in Chinese))
11 林长,张秀莲. 非定常约束下Tzénoff方程的推广. 上海力学, 1991,12(1):35~40 (Lin Z, Zhang X L. Extension of Tzénoff equation with nonholonomic constraints.ChineseQuarterlyofMechanics, 1991,12(1):35~40 (in Chinese))
12 李元成. 包含伺服约束的非完整系统的Ценов方程. 贵州师范大学学报, 1993,11(3):17~24 (Li Y C. Ценов equation of nonholonomic mechanical systems containing servo restriction.JournalofGuizhouNormalUniversity, 1993,11(3):17~24 (in Chinese))
13 陈刚. 导数空间非完整系统任意阶Tzénoff方程及其第一积分. 华中师范大学学报, 1993,27(S1): 97~101 (Chen G. Tzénoff equation for arbitrary order nonholonomic systems in derivative space and its first integral.JournalofHuazhongNormalUniversity, 1993,27(S1):97~101 (in Chinese))
14 郭冠平. 高阶非完整力学系统相对于非惯性系的Tzénoff方程. 浙江师范大学学报, 1996,19(1):31~36 (Guo G P. Tzénoff equation of high-order nonholonomic systems relative to noninertial frame.JournalofZhejiangNormalUniversity, 1996,19(1):31~36 (in Chinese))
15 郑世旺,贾利群. 完整系统Tzénoff方程的Mei对称性和守恒量. 物理学报, 2007,56(2):661~665 (Zheng S W, Jia L Q. Mei symmetry and conserved quantity of Tzénoff equations for nonholonomic systems.ActaPhysicaSinica, 2007,56(2):661~665 (in Chinese))
16 Савин Г Н, Путята Т В, Фрадлин. Очерки Раэвития Некоторых Фундаменталъных Проблем Механики. Кцев : Наукова Думка, 1964
17 Papastavridis J G. Analytical Mechanics. New York: Oxford Univ. Press, 2002
18 Mac Millan W D. Dynamics of Rigid Bodies, New York: Mac Graw-Hill, 1936
19 周培源. 理论力学. 北京 : 人民教育出版社, 1952 ; 北京 : 科学出版社, 2012(Zhou P Y. Theoretical mechanics. Beijing: People's Education Press, 1952 (in Chinese))
20 Добронравов ВВ. Принципы Даламбера Лагранфа И Гельдера И Уравнения Двифения Механических Систем С Неголономными Свяэями. Механика 104, Москва : МВТУ, 1961
21 梅凤翔. 非完整系统力学的历史与现状. 力学与实践, 1979,1(4):6~10 (Mei F X. The history and present situation of nonholonomic mechanical systems.MechanicsinEngineering, 1979,1(4):6~10 (in Chinese))
22 Mei F X. Extension of the Mac Millan′s equations to nonlinear nonholonomic mechanical systems.AppliedMathematicsandMechanics, 1984,5(5):1633~1638
23 罗勇,刘桂林,梅凤翔. 变质量高阶非完整系统的Mac Millan方程. 兵工学报, 1988,2:47~55 (Luo Y, Liu G L, Mei F X. Mac Millan equations for variable mass systems with high-order non-holonomic constraints.ActaArmamentarii, 1988,2:47~55 (in Chinese))
24 陈立群. 广义Mac Millan方程对变质量非完整力学系统的推广. 固体力学学报, 1990,11(3):277~283 (Chen L Q. Extension of the generalized Mac Millan equation to variable mass nonholonomic mechanical systems.ActaMechanicaSolidaSinica, 1990,11(3):277~283 (in Chinese))
25 陈立群,王铁光. 变质量可控力学系统的广义Mac Millan方程. 东北工学院学报, 1992,12(1): 62~68 (Chen L Q, Wang T G. Generalized Mac Millan equation for variable mass controllable mechanical systems.JournalofNortheasternUniversityofTechnology, 1992,12(1):62~68 (in Chinese))
26 陈立群. 准坐标下的Mac Millan方程. 力学与实践, 1989,11(5):51~53 (Chen L Q. Mac Millan equations in quasi-coordinates.MechanicsinEngineering, 1989,11(5):51~53 (in Chinese))
27 张解放. 带任意阶非完整约束的力学系统准坐标下的Mac Millan方程. 科学通报, 1987,32(16):1279~1279 (Zhang J F. Mac Millan equations in quasi-coordinates for mechanical systems with arbitrary order nonholonomic constraints.ChineseScienceBulletin, 1987,32(16):1279~1279 (in Chinese))
28 罗绍凯. 广义事件空间中非完整非有势系统的Mac Millan方程. 成都大学学报, 1991,1:30~39 (Luo S K. Mac Millan equation of nonholonomic nonpotential systems in the generalized event space.JournalofChengduUniversity, 1991,1:30~39 (in Chinese))
29 Добрнравов ВВ. Об основных Полофениях Механики неголономных систем. Механика , МВТУ, 1955: 50~74
*The project supported by the National Natural Science Foundation of China (10932002, 11272050, 11372169, 11572034)
† Corresponding author E-mail: hnynmnl@163.com
11 September 2016,revised 11 October 2016.
ON THE ЦЕНОВ EQUATIONS AND MAC MILLAN EQUATIONSOF NONHOLONOMIC SYSTEM*
Li Yanmin1†Mei Fengxiang2Wu Huibin3
(1.DepartmentofPhysicsandInformationEngineering,ShangqiuNormalUniversity,Shangqiu476000,China)(2.SchoolofAerospaceEngineering,BeijingInstituteoftechnology,Beijing100081,China)(3.Schoolofmathematics,BeijingInstituteoftechnology,Beijing100081,China)
The Ценов equations and Mac Millan equations are motion equations later appearing in the history of nonholonomic mechanics. These equations not only have the historical significance, but also have the advantage of theory and application. Some relevant history data are provided for the formation and the development of the Ценов equations and Mac Millan equations, and our propositions are given.
analytical mechanics, Ценов equations, Mac Millan equations, history of formation
*国家自然科学基金资助项目(10932002,11272050,11372169,11572034)
10.6052/1672-6553-2017-008
2016-09-11收到第1稿,2016-10-11收到修改稿.
† 通讯作者 E-mail: hnynmnl@163.com

