多频激励磁悬浮能量采集*

王祖尧 丁虎 陈立群

(1.上海大学上海市应用数学和力学研究所, 上海 200072) (2.浙江科技学院理学院, 杭州 310023) (3.上海大学力学系, 上海 200444)

多频激励磁悬浮能量采集*

王祖尧1,2丁虎1†陈立群1,3

(1.上海大学上海市应用数学和力学研究所, 上海 200072) (2.浙江科技学院理学院, 杭州 310023) (3.上海大学力学系, 上海 200444)

研究多频激励下磁力悬浮非线性磁电能量器采集系统的动力学特性.结合谐波平衡法、牛顿迭代法和弧长延伸法近似分析非线性电力耦合的常微分方程组,研究多简谐频激励下系统的非线性稳态幅频响应特征.通过改变激励的频率,研究磁力悬浮非线性振动能量采集器的幅频特性.研究结果表明,多频激励的稳态幅频响应随非线性系数的增大而位移幅频响应的共振峰变小但带宽变宽.另外,还通过对比电学参数对共振响应幅度以及区域的影响,确定了电阻、电感和耦合系数对增强两个共振强度、扩大两个共振区域,也就是提高能量采集的强度和带宽的影响.数值模拟验证了近似解析分析结果.

非线性, 弧长延伸法, 能量采集, 谐波平衡, 多频激励

引言

近年来,许多研究人员对振动能量采集进行了大量的研究[1-5],力图提高振动能量采集的效率和扩大采集的频率范围.研究表明,引入非线性因素能够增加能量采集的强度和带宽.Jiang和Chen[6]研究了SD能量采集器在高斯白噪音激励下的响应,表明几何非线性能量采集改善了能量采集的效率.还可以通过磁力作用引入非线性因素.Zhu和Zu[7]提出了一种新型的磁悬浮能量采集器,实验表明这种设计可以增加能量的采集强度并扩展采集的频带宽度.Mann等人[8]通过单自由度弹簧振子的非线性振动特性分析,对这种磁悬浮的装置的非线性能量采集性能进行了近似解析分析,得到了幅频响应关系.

在已有的能量采集研究中,大多数研究的是单频激励下的能量采集,在实际能量采集系统中,外部激励多为多频激励,即系统存在两个或两个以上的激励源.多频激励容易产生混沌行为,而往往会导致系统振荡或不规则运动,甚至会使系统彻底崩溃.因此,有必要研究多频激励对能量采集系统的影响.人们对多频激励下的系统进行了大量的研究工作.杨德森等人[10]利用多尺度法研究了在多频激励下Duffing系统的幅频响应特性的研究.毕勤胜和陈予恕等人[11]研究了不可通约两周期激励作用下的Duffing方程的响应.董建宁等[12]利用数值方法研究了多频激励作用下Duffing-vander Pol的系统参数对近似解幅频曲线的影响.邹鸿翔[13]等研究多频简谐激励下裂纹梁的非线性振动响应.本文研究文献[7-9]装置中的磁电能量采集系统.进一步建立电力耦合的非线性振动方程组,通过谐波平衡方法和弧长法研究了该强非线性系统在外部多频激励下不同激励频率关系的稳态响应特征.通过直接数值方法加以验证.并对比不同参数的系统响应,揭示系统各电学参数对能量采集效果的影响.

1 磁悬浮能量采集器

如图1给出了磁悬浮能量采集器的示意图.相应的力学模型图和电学模型图如图2所示.通过牛顿第二定律和基尔霍夫定律可到如下控制方程

(1)

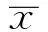
图1 磁悬浮能量采集器的原理图Fig. 1 Schematic of theenergy harvester based on magnetic levitation

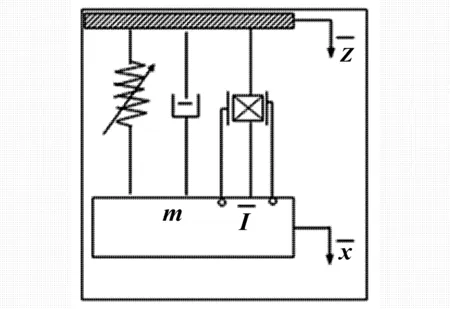
图2 磁力悬浮能量采集系统力学和电学模型图Fig. 2 Amechanical and electrical model schematic of the magnetic levitation energy harvesting system

2 多频激励的谐波平衡法分析

由于磁悬浮能量采集器是强非线性激励系统,这里通过谐波平衡法对方程(1)进行近似求解.为了将分析的问题一般化,首先对方程(1)进行无量纲化,即引入如下无量纲参数

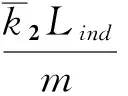
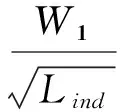
(2)

将方程(2)代入方程(1),得到如下无量纲方程

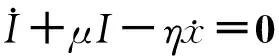
(3)

假设方程(3)的解满足如下形式

(4)

将方程(4)代入方程(3),并令k=2和cos(iωt)和sin(iωt) (i= 0, 1, 2, 3)的系数分别相等,得到下列方程组

b11cω+3a01b21b31k3+a11k1+

3a21b21b31k3/2+a12η-f1=0

(5)

3k3(a012b11+a01a11b21-a01a21b11+a01a21b31-

b212b31-a212b31-b112b31)-a11cω-b11ω2+

b12η1+b11k1=0

(6)

-b11ηω+a12μ+b12ω=0

(7)

a11ηω-a12ω+b12μ=0

(8)

3a012a21k3+2b21cω+3a01a11a31k3+3a01b11b31k3+

a21k1-4a21ω2+a22η-f2=0

(9)

b21k1-4b21ω2-2a21cω+b22η=0

(10)

-b21ηω+a22μ+2b22ω=0

(11)

2a21ηω-2a22ω+b22μ=0

(12)

a113k3/4+a32η+a31k1-9a31ω2=0

(13)

b113k3/4+3a11a21b21k3/2+b32η+b31k1+

学生以及教辅资料中有关这道题的很多解法都是利用特殊情形和极限情形得到答案的,教学中应引导学生发现这类解法的问题并提出如何给出严谨的解法.

(14)

-3b21ηω+a32μ+3b32ω=0

(15)

3a31ηω-3a32ω+b32μ=0

(16)

a01k1+g1+a013k3+

(17)

对于给定的激励频率ω,通过求解方程(5)～(17)中通过牛顿迭代和弧长延长法可以解得方程(4)中的系数.从而可以分别求得方程(3)的位移和电流的表达式,得到均方根位移和电流振幅幅频响应.

系统的电功率可以通过P=μs2计算,而在一个周期T=2π/ω的平均电功率可以表示为

(18)

3 多频激励的幅频特性分析

选取如下系统参数:m= 0.0195kg,c=0.05Ns/m,线性弹性项系数k1=35N/m,非线性弹性系数项k3=13840N/m3,多频激励加速度振幅W1=W2=8m/s2,多频激励的频率比k=2,电阻R=10Ω,电感Lind=0.005H,线圈长度Lcoil=10m,磁通强度B=0.05T.

如图3和图4所示,当k=1时,就是单频激励幅频响应.当k=2和3时,稳态响应振幅在ω=6.7Hz的右边附近出现一个向右弯曲的共振峰,振幅最大值几乎相等,都大于k=1时最大值的一半.当k=2和3时,分别在ω=6.7hz的二分之一和三分之一的附近出现另一个向右弯曲的共振峰.在图4中,平均功率只在两个共振峰附近取得比较大的振幅.

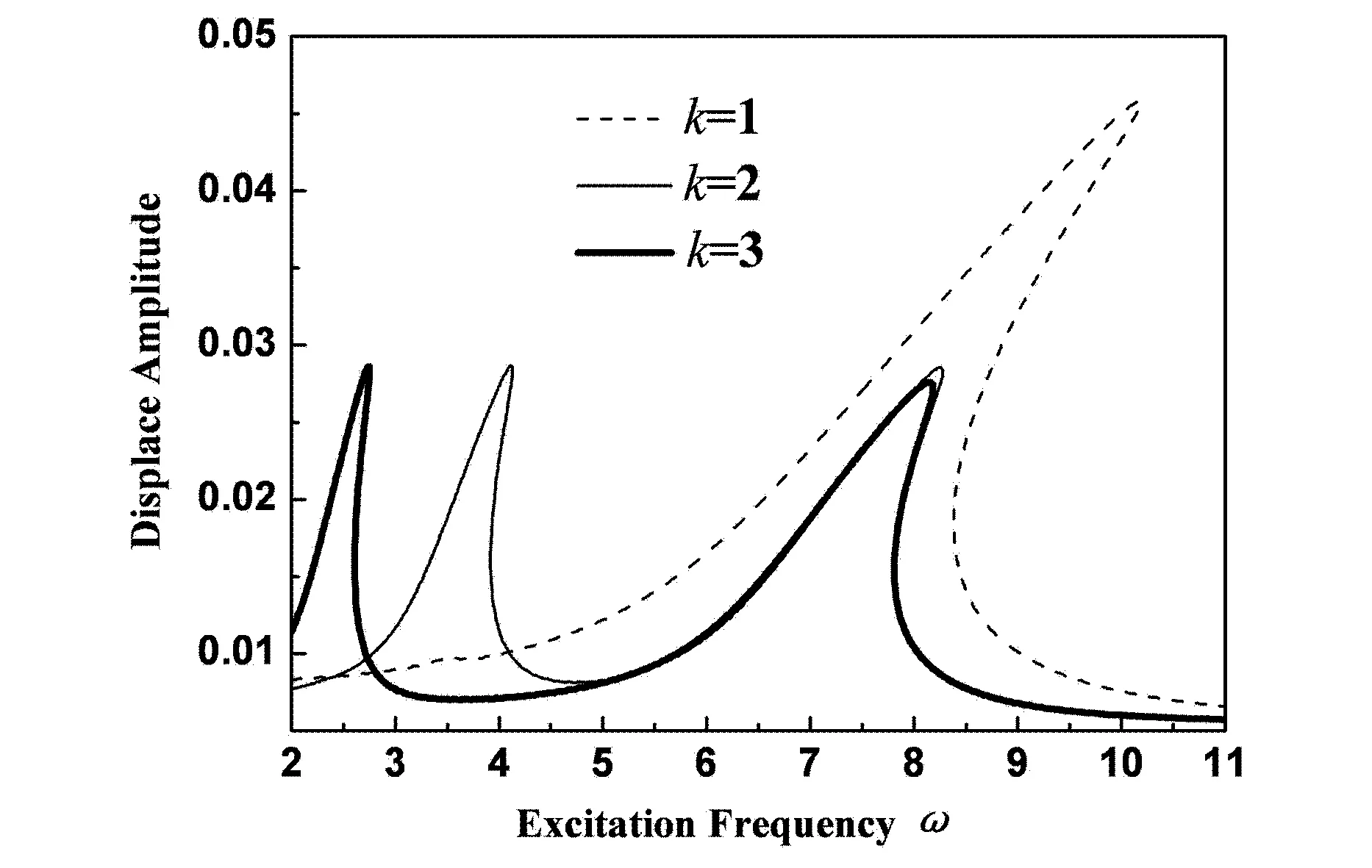
图3 中间磁铁在不同的频率比k下的位移幅频响应Fig. 3 Displacement frequency response of middle magnetdifferent frequency ratio k

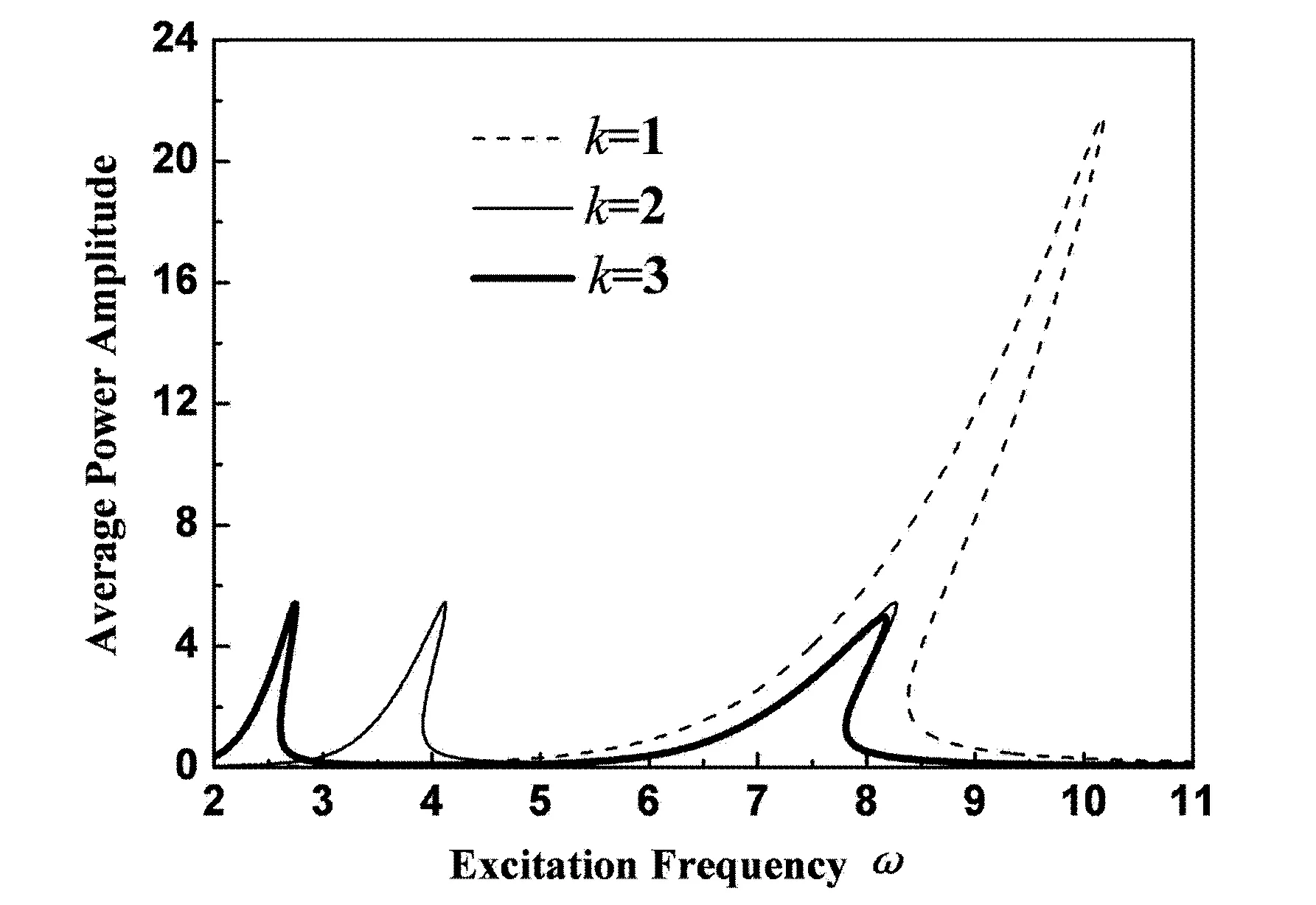
图4 中间磁铁在不同的频率比k下的平均功率幅频响应Fig. 4 Average power frequency response of middle magnet different frequency ratio k

在图5和图6给出频率比k=2时四阶龙格库塔法的直接数值结果与谐波平衡法近似分析结果的对比.数值方法得到的幅频曲线与谐波平衡法得到中间磁铁的幅频曲线一致.

图5 中间磁铁位移幅频响应的数值验证(k=2)Fig. 5 Numerical verification for the displacement frequency response of middle magnet (k=2)

图6 中间磁铁平均功率幅频响应的数值验证(k=2)Fig. 6 Numerical verification for the average power frequency response of middle magnet (k=2)

选取k=2时,选取非线性系数k3分别为13840×0.6、13840和13840×1.4(N/m3).图7给出了多频激励的系统幅频响应曲线.当非线性系数增大时,位移振幅变小,振幅的两个共振峰越向右弯曲和带宽变宽.因此,非线性系数改变可以调节非线性能量采集器在多频激励下的响应振幅和带宽.

图7 中间磁铁在不同非线性系数的位移幅频响应Fig. 7 Displacement frequency response of middle magnet different nonlinear coefficient k3

4 系统电参数对能力采集器的影响

4.1 电感对系统的影响

图8和图9给出了电感Lind分别取为0.003H、0.005H和0.008H时,系统的幅频响应曲线.从图8中发现,改变参数Lind,中间磁铁的位移幅频响应曲线保持不变.但从图9中发现,电感取得越大,中间磁铁的平均功率的幅频响应曲线的两个共振峰越小,而且带宽越宽,并越向右弯曲.

4.2 耦合系数对系统的影响

图10和图11给出了耦合系数η分别取为0.2、0.5和0.8时的幅频响应曲线.从图10中发现,耦合系数越小,中间磁铁的位移的幅频响应曲线的两个共振峰越大,带宽越宽并且越向右弯曲；从图11中发现,耦合系数取得越大,系统平均功率的幅频响应曲线的两个共振峰越大,但是耦合系数取得越小,带宽越宽,并越向右弯曲.

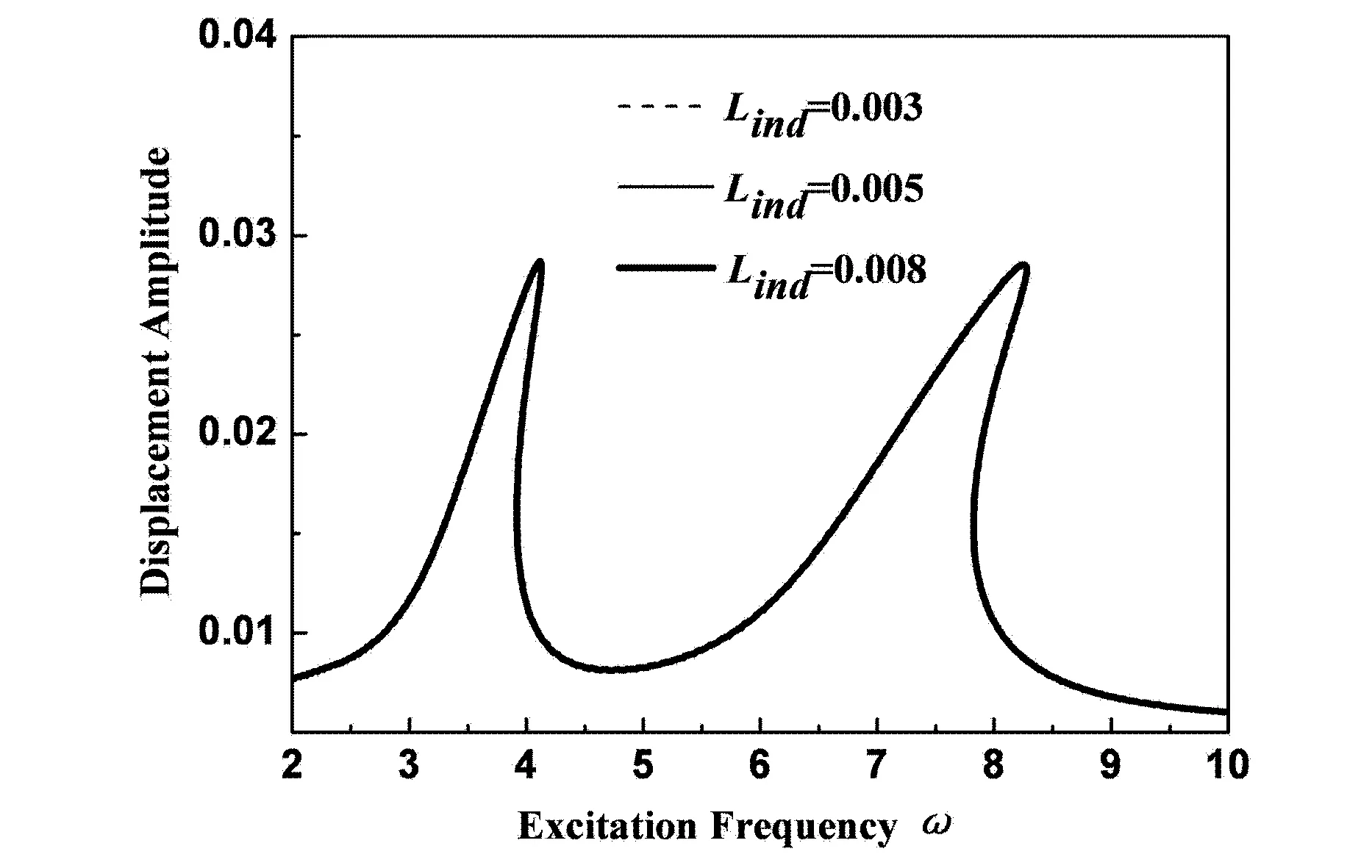
图8 中间磁铁在不同的的电感的位移幅频响应Fig. 8 Displacement frequency response of middle magnet different inductance Lind

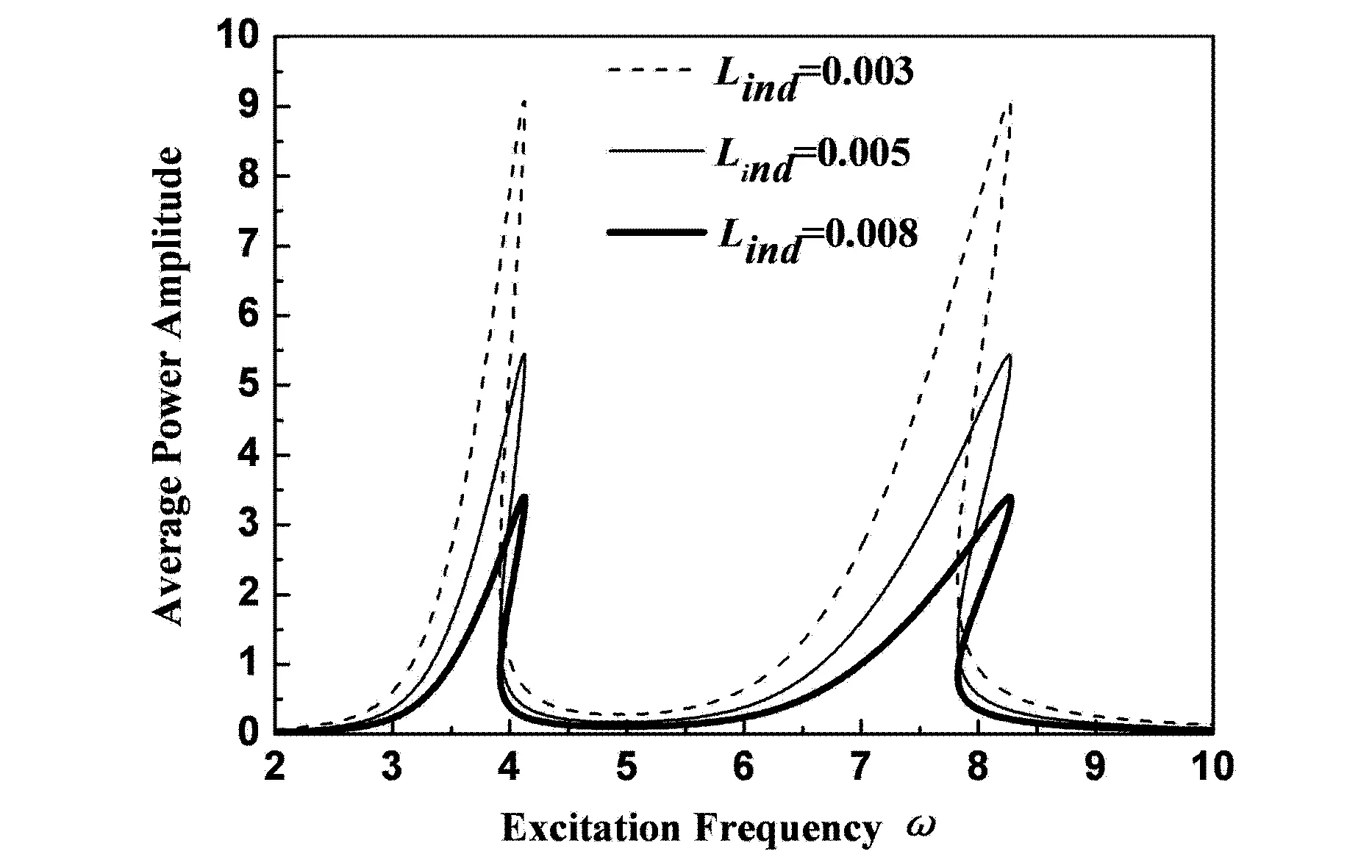
图9 中间磁铁在不同的电感的平均功率幅频响应Fig. 9 Average power frequency response of middle magnet different inductance Lind

图10 中间磁铁在不同的耦合系数的位移幅频响应Fig. 10 Displacement frequency response of middle magnet different coupling coefficient η

图11 中间磁铁在不同的耦合系数的位移幅频响应Fig. 11 Average power frequency response of middle magnet different coupling coefficient η

5 结论

本文研究了一种磁力悬浮非线性能量器采集系统在多频激励下的非线性动力学响应.通过结合运用三阶谐波平衡法、牛顿迭代法和弧长延伸法,近似解析分析能量采集系统在多频激励下中间磁铁的位移和平均功率辐频响应.并通过直接数值方法验证解析分析.研究结果表明,这种磁力能量采集器在多频激励下非线性系数的增大时,位移幅频响应的两个共振峰振幅变小,但两个共振峰的带宽变宽.另外,通过电学参数分析发现,调节电学参数,可以优化得到增强两个共振峰和带宽的宽度,以达到增强振动能量采集效果的目的.

1 Roundy S, Wright P K, Rabaey J. A study of low level vibrations as a power source for wireless sensor nodes.ComputerCommunications, 2003,26(11):1131～1144

2 Mitcheson P D, Yeatman E M, Rao G K, Holmes A S, Green T C. Energy harvesting from human and machine motion for wireless electronic devices.ProceedingsoftheIEEE, 2008,96(9):1457～1486

3 Tang S L P. Recent developments in flexible wearable electronics for monitoring applications .TransactionsoftheInstituteofMeasurementandControl, 2007,29(3-4):283～300

4 Jiang X Z, Wang J, Li YC, et al. Energy harvesting for powering wireless sensor networks in low-frequency and large-force environments.JournalofMechanicalEngineeringScience, 2015,229:1953～1964

5 曹东兴,吴鹏,张伟,姚明辉. 一种新型压电俘能器的振动特性分析及性能研究. 动力学与控制学报, 2015,13(4):300～307 (Cao D X, Wu P, Zhang W, Yao M H. Nonlinear vibration of a novel piezoelectric vibration energy harvester.JournalofDynamicsandControl, 2015,13(4):300～307 (in Chinese))

6 Jiang W A, Chen L Q. Snap-through piezoelectric energy harvesting .JournalofSoundandVibration, 2014,333:4314～4325

7 Zhu Yang, Zu W, Jean A. Magneto electric generator for energy harvesting from the vibration of magnetic levitation.IEEETransactionsonMagnetics, 2012,48(11):3344～3347

8 Mann B P, Sims N D. Energy harvesting from the nonlinear oscillations of magnetic levitation.JournalofSoundandVibration, 2009,319:515～530

9 王祖尧,丁虎,陈立群. 两自由度磁力悬浮非线性振动能量采集研. 振动与冲击, 2016,35(16):57～58 (Wang Z Y, Ding H, Chen L Q. Nonlinear oscillations of a two degree-of-freedom energy harvester of magnetic levitation.JournalofVibrationandShock, 2016,35(16):57～58 (in Chinese))

10 杨德森,董雷,时洁,等. 多频激励Duffing系统振动状态研究. 振动与冲击, 2011,30(12):19～21 (Yang D S, Dong L, Shi J, et al. Duffing system vibration behavior under multi-frequency excitation.JournalofVibrationandShock, 2011,30(12):19～21 (in Chinese))

11 毕勤胜,陈予恕,吴志强. 多频激励Duffing 系统的分岔和混沌. 应用数学和力学, 1998,19(2):113～120 (Bi Q S, Chen Y S, Wu Z Q. Bifurcation in nonlinear Duffing system with multi-frequency external periodic forces.AppliedMathematicsandMechanics, 1998,19(2):113～120 (in Chinese))

12 董建宁,申永军,杨绍普. 多频激励作用下Duffing-van der Pol 系统的分岔分析. 石家庄铁道学院学报, 2006,19(1):62～66(DONG J R, SHEN Y J, YANG S P. Main Resonance of Duffing-Van der Pol system to multi-frequency excitations.JournalofShiJiaZhuangRailwayInstitute, 2006,19(1):62～66 (in Chinese))

13 邹鸿翔,魏克湘,杜荣华,刘迎春. 多频简谐激励下裂纹梁的非线性振动响应. 动力学与控制学报, 2013,11(3):246～251 (Zou H X, Wei K X, Du R H, Liu Y C. Nonlinear dynamic response of a crack beam under high low frequencies co-excitation.JournalofDynamicsandControl, 2013,11(3):246～251 (in Chinese))

*The project supported by the National Natural Science Key Foundation of China (11232009) and the National Natural Science Foundation of China (11372171, 11422214)

† Corresponding author E-mail: dinghu3@staff.shu.edu.cn

17 July 2016, revised 29 August 2016.

ENERGY HARVESTING OF MAGNETIC LEVITATION UNDER MULTI-FREQUENCY EXCITATIONS*

Wang Zuyao1,2, Ding Hu1†, Chen Liqun1,3

(1.ShanghaiInstituteofAppliedMathematicsandMechanics,ShanghaiUniversity,Shanghai200072,China)(2.SchoolofScience,ZhejiangUniversityofScienceandTechnology,Hangzhou310023,China)(3.DepartmentofMechanics,ShanghaiUniversity,Shanghai2004444,China)

This paper studies the nonlinear dynamics of a nonlinear energy harvester of magnetic levitation that uses electromagnetic induction to convert vibration into electrical energy under multi-frequency excitation. The amplitude-frequency response of the energy harvester is investigated by varying the external frequency. The nonlinear equations of electromagnetic-mechanic coupling model are approximately analyzed by using the harmonic balance method and arc-length method. Through changing the excitation frequency, the characteristics of the steady-state amplitude-frequency response containing two resonances are studied. The results show that the resonance peak of displacement amplitude frequency response under multi-frequency excitation is decreased, but the bandwidth is increased with the increase of nonlinear coefficient. Moreover, the effects of the resistance, inductance and coupling coefficient are investigated to determine the influences of the intensity of energy acquisition and the bandwidth. In addition, the approximate analytic results are verified through direct numerical simulations of up sweep and down sweep.

nonlinear, arc-length method, energy harvesting, harmonic balance, multi-frequency excitation

*国家自然科学基金重点项目(11232009)、国家自然基金面上项目(11372171)、国家自然基金优青项目(11422214)

10.6052/1672-6553-2016-064

2016-07-17收到第1稿,2016-08-29收到修改稿.

† 通讯作者 E-mail: dinghu3@staff.shu.edu.cn