含摩擦阻尼器非光滑振动系统的建模与数值仿真*

朱琳 王琪 张润森

(北京航空航天大学航空科学与工程学院, 北京 100083)

含摩擦阻尼器非光滑振动系统的建模与数值仿真*

朱琳 王琪†张润森

(北京航空航天大学航空科学与工程学院, 北京 100083)

研究了含干摩擦粘/弹性构件的两类非光滑减振器的动力学问题.首先,建立了含摩擦粘性构件和含摩擦弹性构件的力学模型,其中摩擦模型采用Coulomb干摩擦模型,不计弹性构件和粘性构件的质量,给出了该构件粘性力和弹性力的计算方法,通过控制摩擦阻尼器的正压力调整混合阻尼器的粘性力的最大值和弹簧力的最大值.分别建立了含摩擦粘/弹性阻尼器的单自由度和二自由度振动系统的动力学方程,通过数值仿真,首先分析了动、静摩擦系数对含摩擦粘/弹性构件单自由度振动系统动力学特性的影响,然后分析了含摩擦粘/弹性构件二自由度振动系统的动力学特性,仿真结果表明,通过控制摩擦阻尼器受到的的正压力获得更好的减振效果.

非光滑动力学, 摩擦阻尼器, Coulomb干摩擦, 数值仿真

引言

在航空、航天、机械、车辆、建筑等诸多领域中,减振始终是人们关注的重要问题.例如,在建筑领域,为减少地震对建筑结构带来的损害,人们发展并运用了结构抗震技术和结构减震技术.然而,单纯运用结构抗震技术,比如通过提高构件的强度来减少结构振动,会使得建造成本增加.相比之下,采用结构减震技术,由附加的结构吸收大部分外荷载带来的能量,可以节省许多建造成本.结构减震控制技术可分为被动控制、半主动控制、主动控制、混合控制和智能控制[1].其中被动控制具有成本低和维护方便等优点.

近十年来,Bakre等人[2]采用数值方法研究了调频质量阻尼系统(TMD)的参数优化问题.Brizard等人[3]研究并设计了一种含摩擦的弹性减振构件以减少发动机的振动对运载火箭的影响.Minagawa等人[4]将含摩擦的粘性构件用于建筑物的减振,分析了在地震波作用下结构的动力学响应,以及该构件吸收地震波的能力.Chung等人[5]通过数值方法研究了含摩擦的半主动控制TMD系统,通过控制摩擦力提高系统的减振效果.Weber等人[6]设计了一个TMD与磁流变阻尼器共同工作的结构,使得主结构的振动减少60%.Wang等人[7,8]研究了含摩擦的TMD系统在机械加工中的减振效果.

Brizard和Minagawa分别建立了含摩擦的弹性减振构件和含摩擦的粘性减振构件的力学模型,分析了两种构件单独用于结构上的减振效果,其中摩擦阻尼器的摩擦模型采用了Coulomb干摩擦模型,但假设了动、静摩擦系数相同,且未研究两种构件共同用于结构时的减振效果.Chung、Weber和Wang各自设计并分析了在主体结构和子结构之间放置含摩擦构件的TMD系统的减振效果,但未研究将含摩擦的减振构件放置在主体结构上的减振效果.

为研究TMD系统中含摩擦的非光滑粘/弹性减振构件共同作用在主体结构上的减振特性,本文将首先建立含摩擦(动、静摩擦系数不相等)非光滑粘/弹性构件的力学模型；然后给出含摩擦的非光滑粘/弹性构件单自由度振动系统的动力学方程和含摩擦的非光滑粘/弹性构件二自由度TMD系统的动力学方程；最后通过算例,利用数值仿真方法分析了含摩擦的非光滑粘/弹性构件对上述系统减振的效果.

1 非光滑减振器动力学模型

1.1 摩擦阻尼器的摩擦模型

摩擦模型有很多种,其中Coulomb干摩擦模型是既简单又能较好地反映摩擦特性的摩擦模型[9].本文研究的非光滑减振器采用的是Coulomb干摩擦模型.

图1 干摩擦阻尼器的模型Fig. 1 Damper model with dry friction

(1)

(2)

1.2 含摩擦的非光滑粘/弹性构件的力学模型

摩擦阻尼器与其他构件串联成为混合阻尼器,这在实际工程中十分普遍.含摩擦粘性构件和含摩擦弹性构件的力学模型如图2所示,构件质量通常忽略不计[13].

设粘性构件两端点的坐标分别用x1和xc表示,FNC为其摩擦片的正压力,如图2(a)所示；弹性构件两端点的坐标分别用x1和xk表示,FNK为其摩擦片的正压力,如图2(b)所示.

图2 (a)含干摩擦粘性构件的模型；(b)含干摩擦弹性构件的模型Fig. 2 (a) Viscous damper with friction; (b) Spring damper with friction

图2(a)所示的含干摩擦粘性构件的阻尼力与摩擦片是否滑动有关.

(3)

(4)

式中,

(5)

(6)

下一步摩擦片是否滑动可由下式判断:

(7)

同理,图2(b)所示的含干摩擦弹性构件的弹性力也与摩擦片是否滑动有关.

(8)

式中,

(9)

(10)

(11)

式中,

(12)

下一步摩擦片的滑动速度可用下式判断:

(13)

下一步的xk(ti+1)可表示为:

xk(ti+1)=x1(ti)+Ffk1(ti)/k2

(14)

1.3 单自由度非光滑振动系统的力学模型

图3(a)是单自由度非光滑振动系统的力学模型.设滑块质量为m1,左侧与刚度系数为k1的弹簧和阻尼系数为c1的阻尼器连接,右侧与含摩擦的非光滑粘/弹性构件连接,滑块的水平坐标为x1,在外激励F1(t)的作用下运动.

图3 (a)单自由度非光滑振动系统模型；(b)m1受力示意图Fig. 3 (a) Non-smooth vibration system with 1 DOF; (b) Force diagram of m1

(15)

式中,

F1(t)=m1Asin(ωt)

(16)

(17)

其中A,ω为常量.

1.4 二自由度非光滑振动系统(TMD)的力学模型

图4(a)所示的二自由度非光滑振动系统是在图3(a)所示的力学模型基础上增加了一个线性质量-弹簧-阻尼子系统.两个滑块相对基座的水平坐标分别为x1和x2.

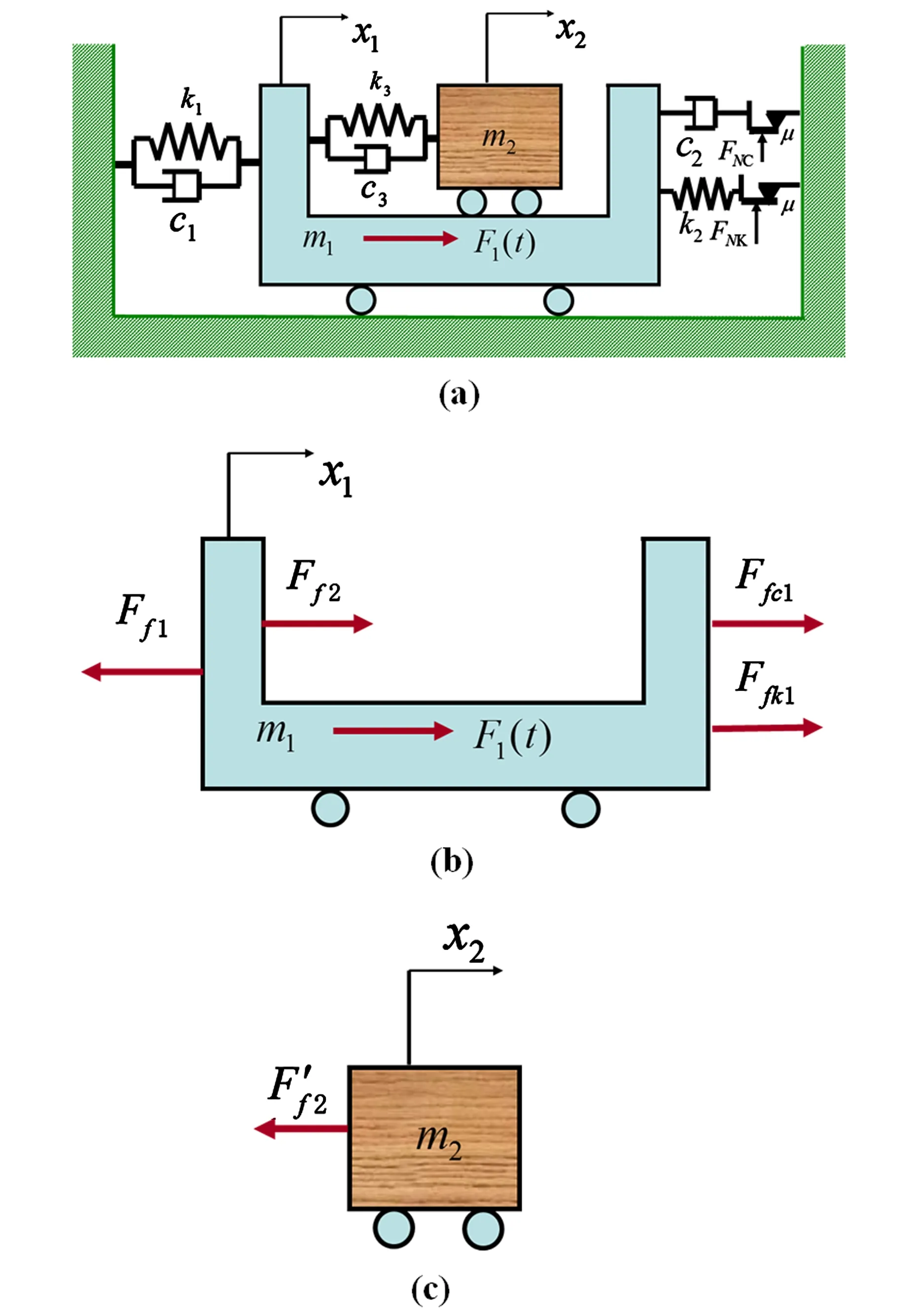
图4 (a)二自由度非光滑振动系统的力学模型；(b) m1受力示意图；(c) m2受力示意图Fig. 4 (a)Non-smooth vibration system with 2 DOF; (b) Force diagram of m1; (c) Force diagram of m2

两滑块的受力如图4(b)和(c)所示,其动力学方程为:

(18)

式中,

k3(x1(t)-x2(t))

(19)

由于摩擦力的存在,上述动力学方程是不连续,不易用解析方法分析其动力学特性,通常采用数值方法来分析.

2 数值仿真分析

2.1 对动、静摩擦系数的讨论

Brizard和Minagawa等人在研究含摩擦粘/弹性减振器时,假设了动、静摩擦系数相同[3-4],而在现实中动摩擦系数通常小于静摩擦系数.本文以图3所示系统为例分析动静摩擦系数对其幅频特性的影响.设外激励频率ω范围为：0.0～20.0rad/s,且相关参数为：

A=10m/s2,m1=5.0kg,k1=500.0N/m,c1=5.0Ns/m,k2=110.0N/m,c2=17.0Ns/m,FNK=74.53N,FNC=121.88N.

分别取μ0=μ=0.22和μ=0.22,μ0=0.3时,图5给出了外激励频率在8.0～14.0rad/s范围内的幅频特性曲线.

图5 不同摩擦系数时m1的幅频响应图Fig. 5 Amplitude response of m1when μ0=μ and μ0>μ

从仿真结果可以看出,在μ0=μ和μ0>μ两种情况下,幅频特性曲线不同.最大幅值由0.2215m变为0.1909m,幅值减小16%,对应的外激励频率由10.6rad/s变成10.4rad/s.

2.2 单自由度非光滑振动系统的仿真分析

系统如图3所示,设m1,k1,c1,k2,c2等参数同上,取μ=0.22, μ0=0.3.

由文中1.2和1.3中的公式可知,对于本文给出的单自由度非光滑振动系统的动力学方程是分段线性的,理论上可给出每段方程的解析解(积分常数由初始条件确定).由于判断滑动摩擦片stick-slip状态切换的表达式比较繁琐,且每个分段给出的动力学方程解析解的初始条件均要由前一段方程解的末端运动状态确定,由此导致动力学方程解析解的表达式不易直观地体现该系统的振动特性.在此,本文采用数值分析方法来研究其振动特性.

下面分五种情况进行数值仿真分析：

Case1：FNK=0.0N, FNC=0.0N；

Case2：FNK=0.0N, FNC=128.23N；

Case3：FNK=180.0N, FNC=0.0N；

Case4：FNK=74.53N, FNC=121.88N；

Case5：FNK和FNC充分大,摩擦片无滑动.

图6为五种情况下,该振动系统的幅频特性,其中横坐标为外激励频率,纵坐标为振幅.在Case1的条件下,含摩擦阻尼器未发挥作用,此时系统的阻尼比为0.05[14],最大幅值为1m,对应的外激励频率为10rad/s.在Case2的条件下,该系统的最大振幅为0.3073m,对应的外激励频率为9.9rad/s.在Case3的条件下,该系统的最大振幅为0.5685m,对应的外激励频率为10.7rad/s.在Case4的条件下,两个摩擦阻尼器在外激励频率为10～11.8rad/s的范围内其摩擦片会出现stick-slip现象,如图7所示；该系统的最大振幅为0.1909m,对应的外激励频率为10.4rad/s.在Case5的条件下,摩擦阻尼器的摩擦片未发生滑动,此时该系统的阻尼比为0.2,最大幅值为0.21m,对应的外激励频率为10.6rad/s.由此可见,可以通过控制含摩擦阻尼器摩擦片的正压力来改变系统的阻尼和刚度,以实现对系统振动的控制.

图6 情况1-5时m1的幅频响应图Fig. 6 Amplitude response of m1in the cases of 1-5

图7 ω=11 rad/s时和的时间历程图Fig. 7 Time history of and when ω=11rad/s

2.3 二自由度非光滑振动系统(TMD)的仿真分析

振动系统如图4所示,设m1,k1,c1,k2,c2,μ,μ0同上,m2=0.5kg,k3=40.0N/m,c3=1.9Ns/m.

下面分五种情况进行数值仿真分析：

Case6：FNK=0.0N, FNC=0.0N；

Case7：FNK=0.0N, FNC=91.58N；

Case8：FNK=129.96N, FNC=0.0N；

Case9：FNK=56.26N, FNC=91.11N；

Case10：FNK和FNC充分大,摩擦片无滑动.

图8 情况6-10时m1的幅频响应图Fig. 8 Amplitude response of m1 in the cases of 6-10

图8为主体滑块m1的幅频特性曲线,其中横坐标是外激励频率,纵坐标为主体滑块的振幅.在Case6的条件下,含摩擦减振器不发挥作用,振幅的两个峰值分别为0.3437m和0.3289m,对应的外激励频率分别为8.4rad/s和10.3rad/s.在Case7的条件下,主体滑块振幅的两个峰值为0.196m和0.1672m,对应的外激励频率分别为7.7rad/s和10.5rad/s.在Case8的条件下,主体滑块振幅的峰值为0.2766m,对应的外激励频率为11rad/s.在Case9的条件下,主体滑块振幅的两个峰值为0.1495m和0.1493m,对应的外激励频率分别为8rad/s和11.4rad/s.在Case10的条件下,摩擦阻尼器的摩擦片始终不滑动,主体滑块振幅的两个峰值分别为0.1544m和0.1503m,对应的外激励频率分别为8.1rad/s和11.1rad/s.由此可见,将非光滑阻尼器与吸振器(m2,k3,c3)综合使用能得到更好地减振效果.关于系统参数对减振效果进一步分析,可通过无量纲化对系统进行动力学仿真,可得到更加全面细致的分析结果.

3 结论

本文研究了含摩擦的非光滑粘/弹性构件对两种非光滑振动系统的减振效果.

本文给出了含Coulomb干摩擦的粘性构件和弹性构件的力学模型以及相应的算法,建立了含摩擦粘/弹性构件的单自由度振动系统和二自由度振动系统的动力学方程.

数值仿真表明,当摩擦片的动、静摩擦系数不同时,其动力学特性是不同的;认为动、静摩擦系数相同,既不符合事实,也不能真实地反映系统动力学特性.

通过数值仿真,分析了含摩擦粘/弹性构件对振动系统幅频特性的影响,改变摩擦片的正压力可以改变系统的刚度和阻尼,从而提高减振效果；单自由度振动系统的幅值降到0.1909m,与原系统(无摩擦粘弹性构件的振动系统)相比最大振幅降低了80.91%；二自由度振动系统的幅值降到0.1495m,与原系统相比最大振幅降低了85.05%.因此,可利用含摩擦的非光滑粘/弹性构件,通过控制摩擦片的正压力提高系统的减振效果.

1 赵鸿铁,徐赵东,张兴虎. 耗能减震控制的研究,应用与发展. 西安建筑科技大学学报(自然科学版), 2001,23(1):1～5 (Zhao H T, Xu Z D, Zhang X F. Study, application and development of energy dissipation and damping control.JournalofXi′anUniversityofArchitecture&Technology, 2001,23(1):1～5 (in Chinese))

2 Bakre S V, Jangid R S. Optimum parameters of tuned mass damper for damped main system.StructuralControl&HealthMonitoring, 2007,14(3):448～470

3 Brizard D, Besset S, Jézéquel L, et al. Design and test of a friction damper to reduce engine vibrations on a space launcher.ArchiveofAppliedMechanics, 2012,83(5):799～815

4 Minagawa K, Fujita S, Kawamura T, et al. Seismic response analysis of industrial building with viscous-friction hybrid dampe. In: ASME 2013 Pressure Vessels and Piping Conference. 2013:V008T08A039

5 Chung L L, Lai Y A, Yang C S W, et al. Semi-active tuned mass dampers with phase control.JournalofSound&Vibration, 2013,332(15):3610～3625

6 Weber F. Semi-active vibration absorber based on real-time controlled MR damper.MechanicalSystems&SignalProcessing, 2014,46(2):272～288

7 Wang M, Zan T, Yang Y, et al. Design and implementation of nonlinear TMD for chatter suppression: An application in turning processes.InternationalJournalofMachineTools&Manufacture, 2010,50(5):474～479

8 Wang M. Feasibility study of nonlinear tuned mass damper for machining chatter suppression.JournalofSound&Vibration, 2011,330(9):1917～1930

9 刘丽兰,刘宏昭,吴子英等. 机械系统中摩擦模型的研究进展. 力学进展, 2008,38(2):201～213 (Liu L L, Liu H Z, Wu Z Y, et al. An overview of friction models in mechanical system.AdvancesinMechanics, 2008,38(2):201～213 (in Chinese))

10王琪,庄方方,郭易圆等. 非光滑多体系统动力学数值算法的研究进展. 力学进展, 2013,43(1):101～111 (Wang Q, Zhuang F F, Guo Y Y, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems.AdvancesinMechanics, 2013,43(1):101～111 (in Chinese))

11Zhuang F F,Wang Q. Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints.MultibodySystemDynamics, 2013,29(4):403～423

12Acary Vincent,Brogliato Bernard. Numerical methods for nonsmooth dynamical systems. Berlin: Springer-Verlag, 2008

13李少康. 控制工程基础. 西北工业大学出版社, 2005 (Li S K. Fundamentals of control engineering. Northwest Industrial University Press, 2005 (in Chinese))

14GB 50011-2010建筑抗震设计规范. 北京：中国建筑工业出版社, 2010 (Code for seismic design of building (GB 50011-2010). Beijing: China Building Industry Press, 2010 (in Chinese))

*The project supported by the National Natural Science Foundation of China (11372018)

† Corresponding author E-mail: bhwangq@sina.com

25 September 2016,revised 2 November 2016.

MODELLING AND SIMULATION OF THE NON-SMOOTH VIBRATION SYSTEMS WITH FRICTION DAMPERS*

Zhu Lin Wang Qi†Zhang Runsen

(SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China)

The dynamic behavior of vibration systems with hybrid dampers is investigated in this paper. Two types of hybrid dampers are introduced, where one is viscous damper with friction and the other is spring damper with friction. The Coulomb′s law of dry friction is used to describe frictional forces in these hybrid dampers and hybrid damper mass is ignored. The numerical methods for computing damp forces of these two hybrid dampers are given. The amplitudes of viscous forces and spring forces at hybrid dampers can be changed by controlling normal forces at hybrid dampers, respectively. The dynamic equations of 1-DOF and 2-DOF vibration systems with the hybrid dampers are then obtained, respectively. The simulation for the 1-DOF vibration system with hybrid dampers is taken to study the influence of the static friction coefficient and dynamic friction coefficient. The dynamical behavior of the 2-DOF vibration system with hybrid dampers is then analyzed. The amplitude response curves of these vibration systems are also given. The simulation results show that the non-smooth vibration systems with hybrid dampers can achieve better properties of reducing vibration amplitude by controlling normal forces at friction dampers.

non-smooth dynamics, frictional damper, Coulomb′s dry friction, numerical simulation

*国家自然科学基金资助项目(11372018)

10.6052/1672-6553-2016-059

2016-09-25收到第1稿,2016-11-02收到修改稿.

† 通讯作者 E-mail: bhwangq@sina.com