基于柔性关节机械臂振动的空间非合作目标质量辨识

李鑫宇 韩艳铧

(南京航空航天大学航天学院, 南京 210016)

基于柔性关节机械臂振动的空间非合作目标质量辨识

李鑫宇 韩艳铧†

(南京航空航天大学航天学院, 南京 210016)

针对空间在轨服务任务中捕获的非合作目标的质量辨识问题,提出了一种基于柔性关节机械臂振动频率的质量辨识方法.在该方法中,首先利用操作航天器上的柔性关节机械臂捕获空间非合作目标;然后对操作航天器、柔性关节机械臂与空间非合作目标形成的组合体进行动力学建模;最后通过分析柔性关节机械臂的振动频率来辨识空间非合作目标的质量.数值仿真结果证实了该方法的有效性.

柔性关节机械臂, 空间非合作目标, 组合体, 动力学建模, 质量辨识

引言

空间在轨服务任务中,作为客户系统的目标航天器可以分为合作目标和非合作目标[1].一般地,空间合作目标是指那些可以向其他航天器提供质量特性参数等信息的目标航天器.目前,空间合作目标的在轨服务技术已经比较成熟,并且成功应用于空间站的交会对接等领域.例如,欧空局的SMART-OLEV项目[2]、日本的ETS-VII项目等.而空间非合作目标是指质量特性参数未知的空间物体,包括故障或失效卫星、空间碎片以及敌方航天器[3]等.这类非合作目标的共性是与服务航天器间没有互动的信息交流,进而对捕获后组合体的高精度姿态控制产生不利的影响.因此必须对非合作目标进行准确的质量辨识.

目前,针对非合作目标和组合体的质量辨识问题,国内外学者进行了大量的研究,已经提出了一些辨识方法.Murotsu等[4]研究了空间机器人捕获未知目标后组合体参数辨识问题,提出了基于线动量守恒原理的辨识方法,但该方法只能辨识组合体的惯性参数,不能辨识未知目标的质量.Yoshida等[5]研究了飞轮动量矩误差等问题,提出了一种基于角动量守恒原理解算出空间机器人及各连杆质量参数修正值的方法,并且通过多次修正后得到目标最优估计值.王明等[6]提出了一种基于机械臂运动的组合航天器惯性参数在轨辨识方法.该方法先通过空间机械臂的大范围运动来改变航天器的速度,然后利用动量守恒原理辨识出组合航天器的质量.张帆等[7]利用空间绳系机器人抓捕未知目标,提出了一种利用抓捕后保持阶段的振动特性辨识未知目标参数的方法.首先,根据质量特性参数辨识的需要建立了系统的动力学模型;然后,分析非合作目标和系绳在抓捕保持阶段的姿态运动;最后在非合作目标与本体卫星没有任何信息交互的情况下,利用抓捕阶段目标卫星和系绳特有的振动来辨识非合作目标的质量.张海博等[8]将空间机器人和非合作目标看作整个系统,基于加速度计测量模型,利用递推最小二乘法完成了系统的质量、质心的辨识.因为空间机器人各部分质量特性参数都是已知的,进而可以解算出非合作目标和机械臂末端作用器联合体的质量和质心位置.李冬柏等[9]研究了捕获目标后在轨服务卫星质量和质心位置的辨识问题,提出了利用最小二乘法来辨识卫星的质量和质心的方法.金磊等[10]利用单臂自由漂浮机器人俘获未知目标.该方法可以分为两步：第一步在惯性坐标系下建立机械臂和未知目标的动力学模型,该模型中必然含有线动量和角动量等信息;第二步测量得到不同时刻下单臂机器人线速度和机械臂角速度、关节角,基于动量守恒原理建立含有未知目标质量特性的不同方程,最终完成辨识.该方法有两个优点:一是避免了动量方程组奇异的问题,二是允许系统线动量和角动量为零情况的存在,更具有普遍性.

以上采用动量守恒原理或最小二乘法对非合作目标质量辨识的研究对象大多为非合作目标或与机械臂组成的刚性组合体,且忽略了机械臂的关节柔性.即便如文献[11]所研究的带有柔性连杆的空间机械臂,也只是考虑了连杆柔性而非关节柔性.本文针对非合作目标与柔性关节机械臂组成的刚柔耦合组合体提出了一种利用柔性关节机械臂的振动频率辨识出非合作目标质量的方法,经验证该方法可辨识出刚柔耦合组合体中非合作目标的质量.

1 柔性关节机械臂与非合作目标动力学建模

1.1 问题描述

参考世界各国的SMART-OLEV和DEOS等项目,不失一般性,组合体系统包括操作航天器及安装于其上的空间机械臂和非合作目标,如图1所示.

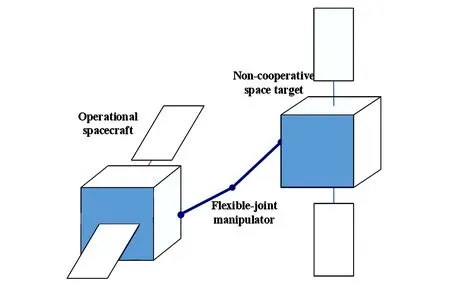
图1 组合体的示意图Fig. 1 Illustration of the combined-body

1.2 组合体动力学建模

为了对捕获的非合作目标进行质量辨识,假设空间坐标系Oxyz为惯性坐标系.在操作航天器的质心处建立本体坐标系O0x0y0z0,O0x0y0平面与Oxy平面共面.点A为机械臂与操作航天器的铰接点,O0x0轴通过O0并指向点A,O0y0轴由O0x0轴逆时针旋转90°得到,O0z0轴符合右手螺旋定则.在本文中只研究航天器在Oxy平面中的运动,故忽略z轴方向.假设非合作目标为一个质点,图2为操作航天器与非合作目标形成的组合体系统的简化模型.

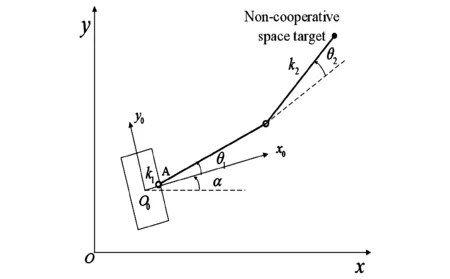
图2 组合体系统的简化模型Fig. 2 Simplified Model of the Combined-body System

假设操作航天器的质量为m,关于其质心的转动惯量为J.在惯性坐标系Oxyz中,质心位置为(x,y).Ox轴逆时针旋转到O0x0轴的角度α,α为操作航天器的俯仰角.操作航天器质心O0到铰接点A间的距离为d.机械臂连杆1和连杆2均为均质杆,质量分别为m1和m2,长度分别为l1和l2,关于各自质心的转动惯量分别为J1和J2.两连杆关节是柔性的,且两个铰接点处的刚度系数分别为k1和k2.连杆2的末端固定着一个质量未知的非合作目标,质量表示为m3.设机械臂连杆1和连杆2由于关节柔性而发生弹性变形的转角分别为θ1和θ2.

非合作目标在坐标系Oxyz中的质心位置坐标为：

(1)

连杆1的质心位置坐标为：

(2)

连杆2的质心位置坐标为：

(3)

操作航天器的平动动能为：

(4)

连杆1和连杆2的平动动能分别为：

(5)

(6)

操作航天器的转动动能为：

(7)

连杆1和连杆2的转动动能分别为：

(8)

(9)

非合作目标的动能为：

(10)

系统的总动能为：

T=TP+TIP+TIIP+TZ+TIZ+TIIZ+T3

(11)

铰接点处的弹性势能分别为：

(12)

(13)

系统总势能为：

V=V1+V2

(14)

系统拉格朗日函数为：

L=T-V

(15)

取系统广义坐标为：

q1≜x,q2≜y,

q3≜α,q4≜θ1,

q5≜θ2.

系统广义力为零,即:

Q1=Q2=Q3=Q4=Q5=0

(16)

将式(4)～(14)代入式(15),然后将式(15)～(16)代入拉格朗日方程:

j=1,2,…,5

(17)

得到系统动力学方程为：

(18)

其中,质量矩阵、阻尼矩阵和刚度矩阵分别为：

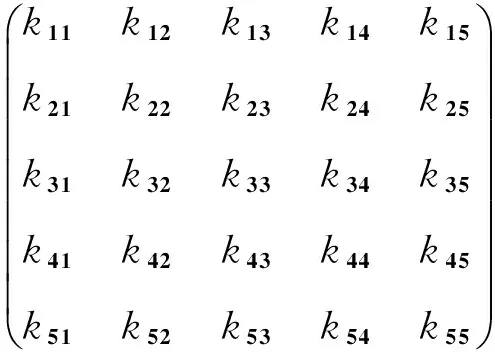
各矩阵元素的具体值见文末附录.

2 非合作目标的质量辨识方法

本文采用刚柔耦合组合体中柔性关节机械臂振动的特征频率来辨识非合作目标的质量.

当机械臂处于平衡位置(即连杆1和连杆2关节没有发生弹性变形)时,关节角为θ1=θ2=0,将系统动力学方程在机械臂平衡位置处进行小扰动线性化得:

(19)

其中,质量矩阵、阻尼矩阵和刚度矩阵分别为：

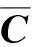
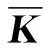
各矩阵元素的具体值见文末附录.

(20)

表1中设定了系统的各参数值.

表1 系统参数Table 1 Parameters of the System

根据表1中设定的参数,系统的特征值为：

(21)

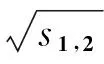
本文首先解算振动的特征频率,然后代入公式(21)求出非合作目标的质量m3.将求解的质量与实际质量进行对比,验证该方法的有效性.

对机械臂的振动进行数值仿真.仿真入口参数如表1所示.

MATLAB的仿真结果为：

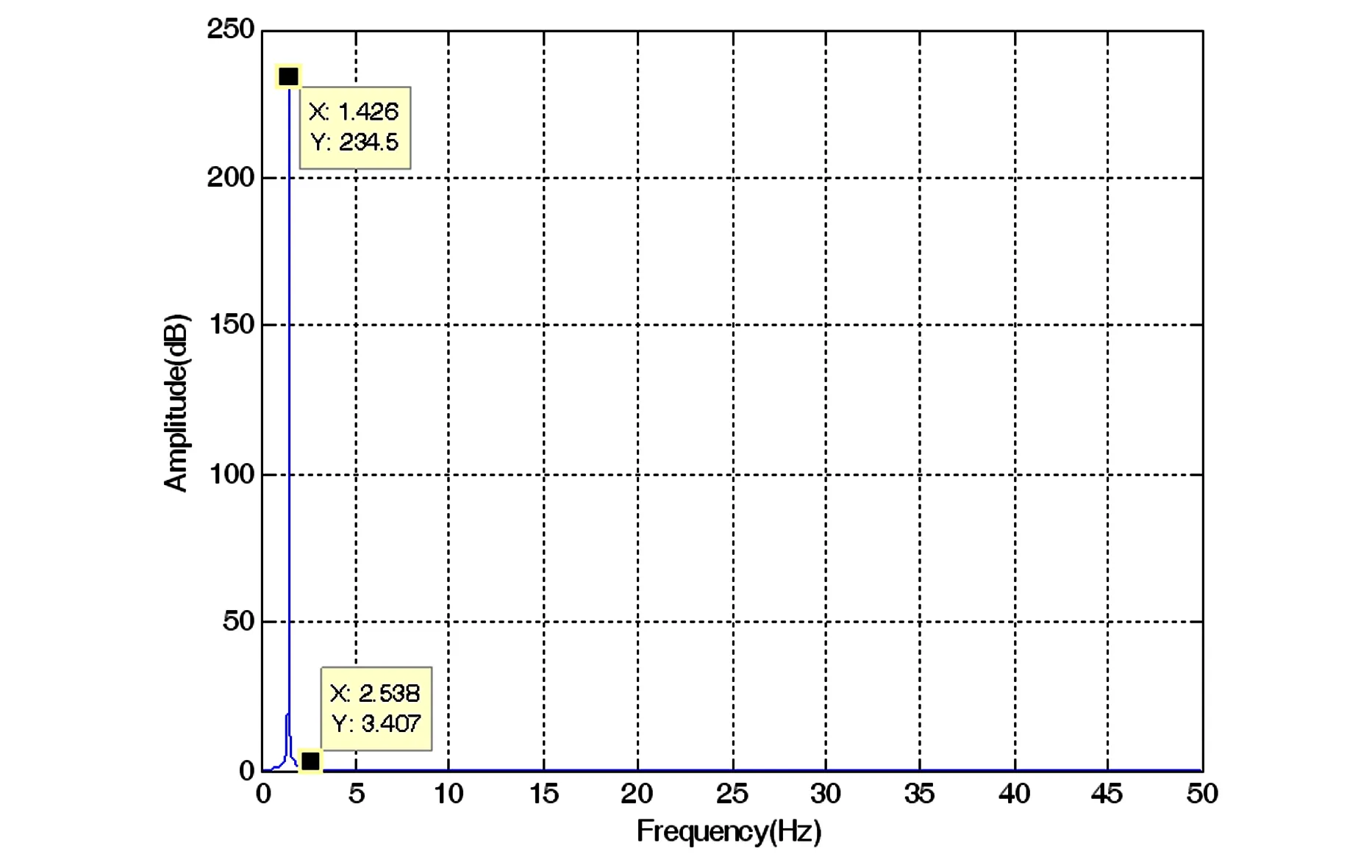
图3 质量为5kg时机械臂振动的特征频率图Fig. 3 Illustration of characteristic frequency of the manipulator′s vibration when m3=5 kg

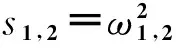
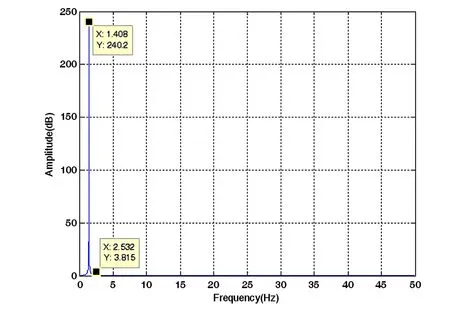
图4 质量为8kg时机械臂振动的特征频率图Fig. 4 Illustration of characteristic frequency of the manipulator′s vibration when m3=8kg

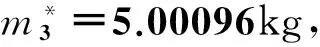
改变非合作目标的质量而不改变系统其它参数取值,采用上述方法进行质量辨识.非合作目标的质量分别取8kg、10kg、15kg和20kg.图4～7为不同质量下的机械臂振动特征频率的仿真结果.

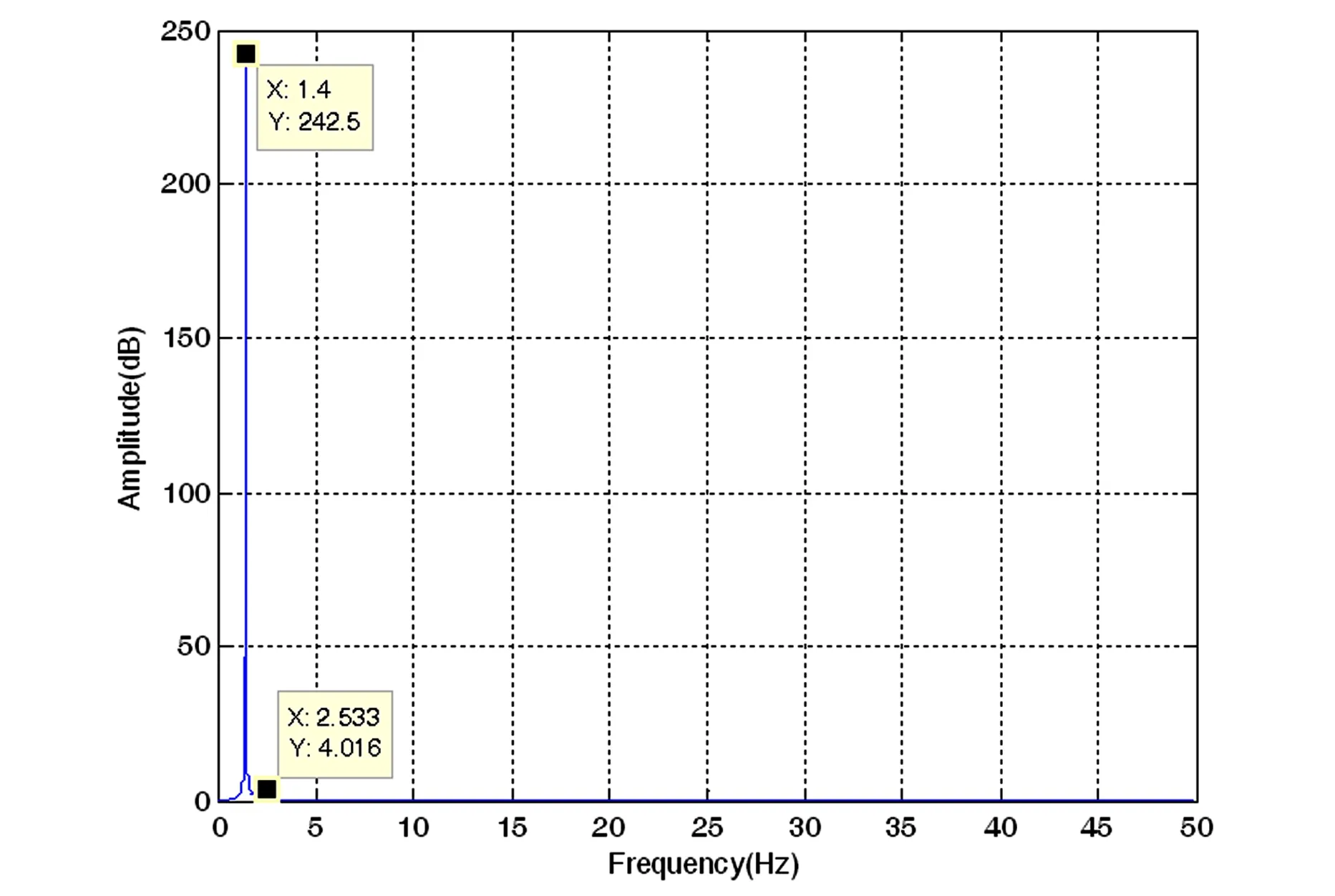
图5 质量为10kg时机械臂振动的特征频率图Fig. 5 Illustration of characteristic frequency of the manipulator′s vibration when m3=10kg

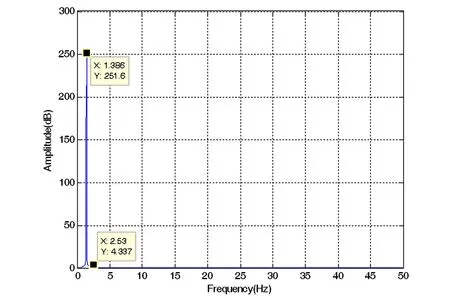
图6 质量为15kg时机械臂振动的特征频率图Fig. 6 Illustration of characteristic frequency of the manipulator′s vibration when m3=15kg

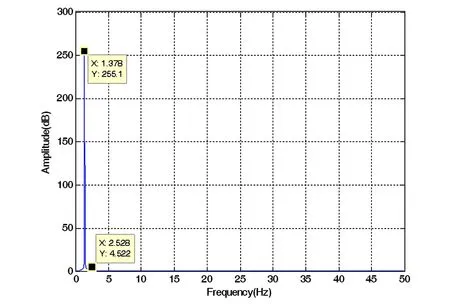
图7 质量为20kg时机械臂振动的特征频率图Fig. 7 Illustration of characteristic frequency of the manipulator′s vibration when m3=20 kg

表2列出了对于不同质量的非合作目标的质量辨识结果.由表2可知,本文所提方法对刚柔耦合组合体中的非合作目标质量辨识误差维持在较小的数量级,在工程中可以接受.

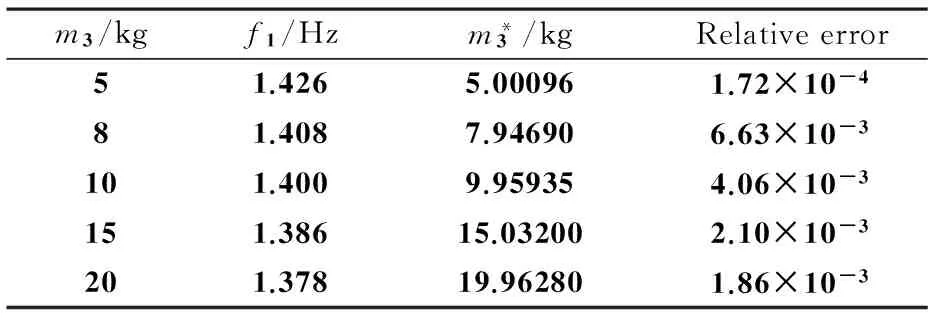
表2 辨识结果Table 2 Results of the Identification

3 结论

本文以带有柔性关节机械臂的操作航天器和空间非合作目标形成的刚柔耦合组合体为研究对象,针对非合作目标质量辨识的问题进行了研究,提出了一种基于柔性关节机械臂振动频率来辨识空间非合作目标质量的方法.该方法仅需机械臂小角度的运动,且通过传感器对机械臂的振动进行记录,然后利用快速傅立叶变换求出振动的特征频率,从而反解出非合作目标的质量.仿真验证了该方法的可行性,可应用于未来的刚柔耦合组合体中非合作目标的质量辨识中.

1 梁斌,杜晓东,李成等. 空间机器人非合作航天器在轨服务研究进展. 机器人,2012,34(2)：242～256 (Liang B, Du X D, Li C, et al. Advances in space robot on-orbit servicing for non-cooperative spacecraft.Robot, 2012,34(2):242～256 (in Chinese))

2 Kaiser C, Sjoberg F, Delcura J M, et al. SMART-OLEV—An orbital life extension vehicle for servicing commercial spacecrafts in GEO.ActaAstronautica, 2008,63(1-4):400～410

3 Kassebom M. ROGER-An advanced solution for a geostationary service satellite.Robot, 2003,35(2):216～225

4 Murotsu Y, Senda K, Ozaki M, et al. Parameter identification of unknown object handled by free-flying space robot.JournalofGuidanceControl&Dynamics, 1992(3):488～494

5 Yoshida K. Inertia parameter identificationfor a free-flying space robot.AIAAJournal, 2002,68(672):AIAA 2002～4568

6 王明,黄攀峰,常海涛. 非合作目标航天器质量特性参数辨识. 飞行力学,2014,32(6)：201～212 (Wang M, Huang P F, Chang H T. Identification of mass characteristic parameters for non-cooperative target spacecraft.FlightDynamics, 2014,32(6):201～212 (in Chinese))

7 张帆,黄攀峰.空间绳系机器人抓捕非合作目标的质量特性参数辨识. 宇航学报,2015,36(6)：630～639 (Zhang F, Huang P F. Inertia parameter estimation for an non-cooperative.JournalofAstronautics, 2015,36(6):630～639 (in Chinese))

8 张海博,王大轶,魏春岭. 空间非合作目标质量特性在轨辨识. 航天控制,2015,33(3)：23～28 (Zhang H B, Wang D Y, Wei C L. On-orbit Identification of mass properties of non-cooperative space target.AerospaceControl, 2015,33(3):23～28(in Chinese))

9 李冬柏,刘闯,王峰. 捕获目标后的在轨服务卫星质量和质心位置辨识.中国空间科学学会2013年空间光学与机电技术研讨会会议论文集, 2013 (Li D B, Liu C, Wang F. Method of mass and centroid identification for user satellites. Proceedings of the 2013 Conference on space optics and mechanical and electrical technology, China Space Science Society, 2013 (in Chinese))

10金磊,徐世杰. 空间机器人抓取未知目标的质量特性参数辨识. 宇航学报,2012,33(11)：1570～1576 (Jin L, Xu S J. Inertial parameter identification of unknown object captured.JournalofAstronautics, 2012,33(11):1570～1576 (in Chinese))

11安凯,王飞飞. 空间机械臂柔性连杆的弯曲形状. 动力学与控制学报,2016,14(1)：48～52 (An K, Wang F F. Bending shape of space manipulator with flexible link.JournalofDynamicsandControl, 2016,14(1):48～52 (in Chinese))

附录：

式(18)中矩阵M、C、K的各元素分别为：

m11=m+m1+m2+m3

m12=0

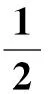
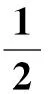
m21=m12

m22=m11

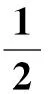
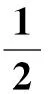
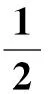
m31=m13

m32=m23

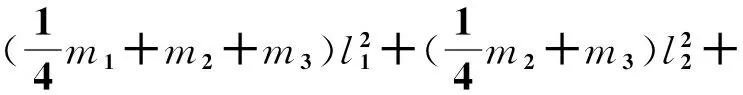
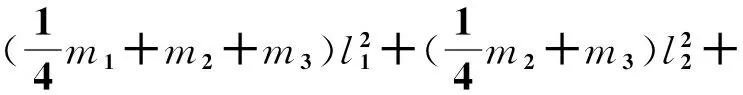
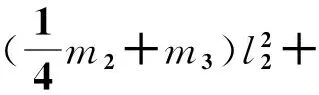
m41=m14

m42=m24

m43=m34

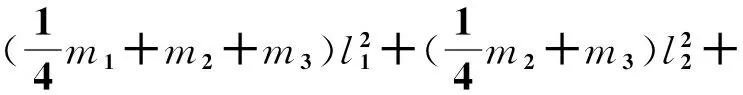
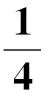
m51=m15

m52=m25

m53=m35

m54=m45

c11=c12=c21=c22=c31=c32=c41=c42=c51=c52=0

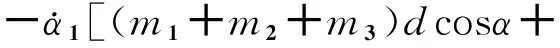
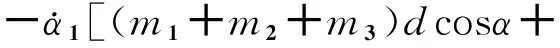
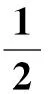
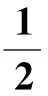
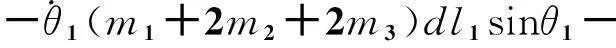
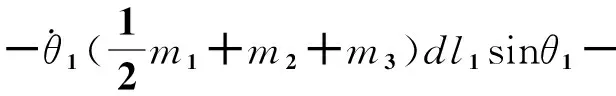
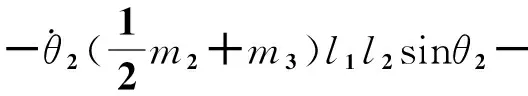
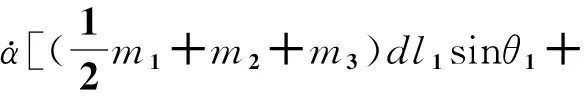
c44=0

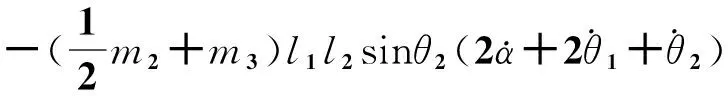
k11=k12=k13=k14=k15=k21=k22=k23=k24=k25=0

k31=k32=k33=k34=k35=k41=k42=k43=k45=k51=k52=k53=k54=0

k44=k1

k55=k2

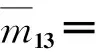
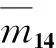
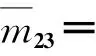
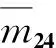
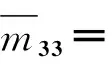
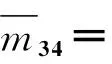
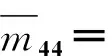
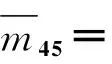
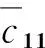
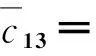
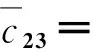
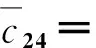
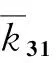
21 July 2016,revised 21 November 2016.

† Corresponding author E-mail: hanyanhua@nuaa.edu.cn

IDENTIFICATION OF MASS PARAMETER OF NON-COOPERATIVE SPACE TARGET BASED ON VIBRATION CHARACTERISTIC OF FLEXIBLE-JOINT MANIPULATOR

Li Xinyu Han Yanhua†

(CollegeofAstronautics,NanjingUniversityofAeronautics&Astronautics,Nanjing210016,China)

For the identification of mass parameter of non-cooperative space target in on-orbit servicing missions, a method of mass identification based on vibration characteristic of the flexible-joint manipulator is proposed. Firstly, the flexible-joint manipulator captures non-cooperative target. Then, the dynamic model of the combined-body formed by operational spacecraft, flexible-joint manipulator and non-cooperative space target is established. Finally, the mass of non-cooperative space target is identified by analyzing the vibration frequency of the manipulator. Numerical simulation results show the effectiveness of the method.

flexible-joint manipulator, non-cooperative space target, combined-body, dynamic modeling, mass identification

10.6052/1672-6553-2016-050

2016-07-21收到第1稿,2016-11-21收到修改稿.

† 通讯作者 E-mail: hanyanhua@nuaa.edu.cn