“三线八角”问题的教法探讨

【摘要】三线八角问题之所以成为学生学习的难点，既与知识本身的复杂程度和学生的认知水平有关，也与教材对知识的呈现方式有关.要突破这一难点，需要在基本图形中准确理解概念的内涵，还要在图形变式中把握概念本质，以及正确建立平行线与角的关联.

【关键词】三线八角；难点突破；教法探讨

如果两条直线被第三条直线所截，就会形成八个角，这就是所谓的“三线八角”，在这八个角中，有“同位角”、“内错角”、“同旁内角”等几个重要概念，因此习惯上把涉及同位角、内错角、同旁内角的几何问题统称为“三线八角”问题.因为绝大部分平行线的性质和判定问题都需要借助于“三线八角”来解决，所以它是平面几何一个传统的重点内容，同时它也是一个难点内容，一些学生往往因在解决三线八角问题时出错而导致学习遇阻，甚至产生厌学和分化.笔者在教学实践中对这一经典内容的教法作了一些探索，叙述于后供大家指正.1“三线八角”问题的教学难点及成因分析

在解决三线八角问题时，学生的出错点主要有两类：一类是不能正确识别图形中的同位角、内错角和同旁内角，另一类是在判定平行线或应用平行线的性质时，不能正确关联线和角.这两类错误有时也相互缠绕，使学生深受其苦.

三线八角问题之所以成为学生学习的难点，既与知识本身的复杂程度和学生的认知水平有关，也与教材对知识的呈现方式有关.

知识本身的因素.三线八角问题涉及三条线、八个角，信息容量大，图形变式多，而在变式图形中，充斥着大量的干扰因素，这是学生感觉困难的根本原因.

学生因素.学生在之前接触的几何问题，除了对基本平面图形和立体图形名称的识别外，系统学习的几何知识主要是线段、射线、直线和角，基本没有涉及变式图形，对图形的认识处于直观感知阶段，读图识图能力较弱，对几何关系的把握能力差，尤其是当接触到包含变式图形的问题时，往往因为外形直观上的改变而无所适从.

教材因素.我校使用的北师大版教材，是在探索两直线平行的条件一课中首次出现“同位角”的概念的，而且只做了简单描述，显然是有意淡化了概念.这样虽然把学生的注意力引向平行线本身，但却导致着学生对“同位角”这一概念的本质认识模糊，也进而导致了进一步研究平行线时学生不能熟练使用三线八角这一有力工具的缺陷.实际上，作为研究平行线的重要工具，三线八角本身是需要学生在学习平行线之前深刻理解并熟练掌握的.2“三线八角”教学难点的突破

2.1在基本图形中准确理解概念的内涵

笔者认为，对初一学生来说，同位角、内错角、同旁内角不是单从字面就能完全理解的概念，需要教师对概念本身的含义进行点拨讲解，使学生准确理解概念是解决问题的基础.

如图1，直线AB、CD被直线EF所截，EF称为“截线”，AB、CD是被截线.

同位角的字面意义是位置相同，识别同位角的关键是学生要领悟两个位置上的“同”即在截线EF的同一旁，被截两直线AB、CD的同一方向.根据以上可以判定图中满足“同位角”条件的有：∠1和∠5、∠2和∠6、∠3和∠7、∠4和∠8.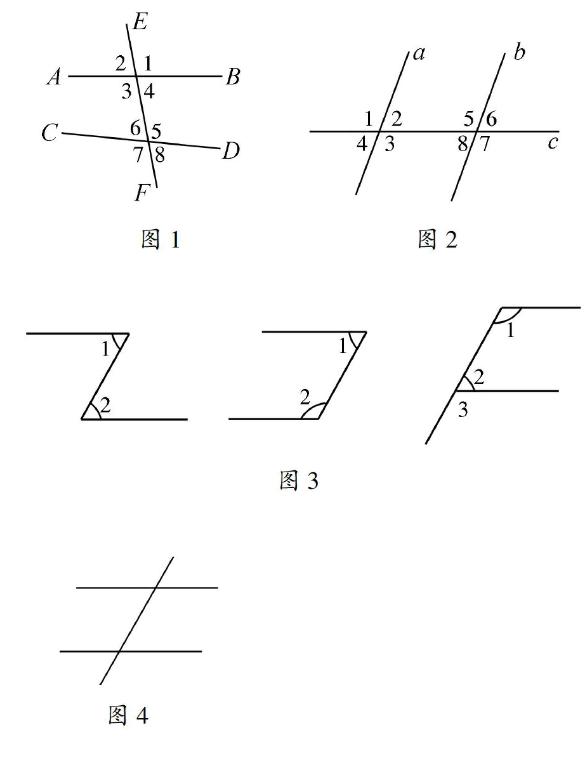

准确辨别内错角的要领是把握两角在被截两直线AB、CD的“内部”，交错在截线EF两旁.据此∠4和∠6、∠3和∠5为“内错角”.

同旁内角：在截线EF同旁，被截两直线AB、CD之间.满足的有∠4和∠5、∠3和∠6.

图2也是标准的基本图形，学生不难从基本图形中识别有关角.

2.2在图形变式中把握概念本质

几何图形千变万化，不管怎样的图形，只要能从中找到“基本图形”，就容易识别三线八角，常用的方法有补齐法和分离法.

（1）补齐法

图3的各图中有同位角、内错角和同旁内角吗？信息的缺失也会导致识别困难.和基本图形相比，这种图形似乎是残缺的、不完整的，刚开始接触这类图形时可用补齐法.比如，只要把图3各图中的相关线段适当延长，都可补齐为图4的基本图形，各类角也就很容易识别了.

（2）分离法

分离法，就是在复杂图形中分离出基本图形，以去除干扰信息（包括交点、线段和角），准确识别三线八角.

当考察∠1和∠2时，将与两角无关的因素去掉，比如按图6的方式把虚框中的图形遮挡，剩下的图形就是图7，此时就很容易看到直线AB、EF被直线CD所截，∠1和∠2在截线CD同旁，被截线AB、EF同方向，所以两角是同位角.类似的方法可识别图5中∠1和∠3是内错角，∠2和∠3是同旁内角.

2.3正确建立平行线与角的关联

学习“三线八角”，不可避免的会遇到由平行线推断相关角的数量关系，或是由角的数量关系推断直线的位置关系的题目，此时正确建立线和角的关联是解决问题的关键.下面看两个例子.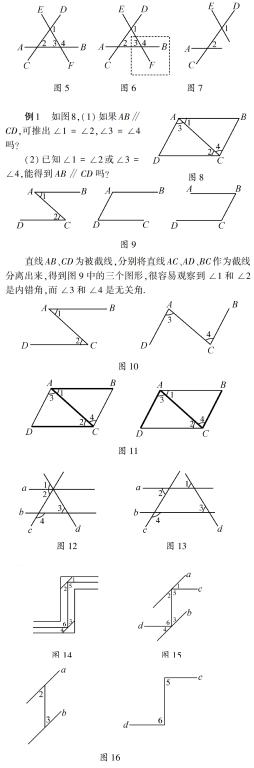

例1如图8，（1）如果AB∥CD，可推出∠1=∠2，∠3=∠4吗？

（2）已知∠1=∠2或∠3=∠4，能得到AB∥CD吗？

直线AB、CD为被截线，分别将直线AC、AD、BC作為截线分离出来，得到图9中的三个图形，很容易观察到∠1和∠2是内错角，而∠3和∠4是无关角.图10图11

反过来，已知∠1=∠2或∠3=∠4，可以把与∠1、∠2或∠3、∠4无关的线段隐藏，分别得到图10中的两个图形，可以看出，由∠1=∠2能推出AB∥CD，而由∠3=∠4不能推出AB∥CD.此类问题，也可用“描线法”分析，即在原图上用红笔或粗笔描绘出∠1和∠2的两边，或∠3和∠4的两边，可分别得到图11中的两个图，这两个图中描了线的突出部分，就分别是图10中的两个图形.

例2如图12，已知∠1=∠2=∠3=59°，求∠4的度数.

此题的难点在于图形中的干扰信息多，学生面对此题，往往不能正确判断由哪对角来判别a，b是平行的，求得a、b平行后，又不能识别哪个角与∠4是关联的？解决此问题的关键是排除干扰信息，解决问题的方法是分离法，比如把图中的线d平移到图13的位置，则立得两个三线八角的基本图形，∠1和∠3的同位角关系以及∠2和∠4的关联性也变得一目了然，问题顺利得到解决.

2.4实际问题数学化

新课程注重数学在实际生活中的应用，因此教材及近几年考试出现了大量以实际生活为背景的题目，解决这类问题的基本方法是把实际问题抽象成数学模型.

例3如图14，潜望镜中的两个镜子是互相平行放置的，光线经过镜子反射时，入射角等于反射角，则有∠1=∠2，∠3=∠4.请解释：为什么进入潜望镜的光线和离开潜望镜的光线是平行的？

由于实际问题情境的限制，虽然图14已经对平行镜面作了“放大”处理，但学生仍不易识别其中的三线八角.此时可以去除无关要素，放大有用信息，把此问题进一步抽象成几何图形，得到图15，这样原题就转化为：已知，如图15，a∥b，∠1=∠2，∠3=∠4，求证：c∥d.

利用分离法，去除无关因素后得到图16，即可由镜面a、b平行得到∠2=∠3，进而通过推理得到∠5=∠6，再由内错角相等得到c、d平行，问题得以顺利解决.

作者简介袁军霞，硕士，荣获青岛开发区新教师优质课比赛二等奖并成功开设区公开课.多次指导学生参加《全国中学生数理化学科能力展示活动》取得省一等奖.