基于轨迹跟踪的动力定位控制器设计*

王述桓 徐海祥 冯 辉 余文曌

(武汉理工大学交通学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)

基于轨迹跟踪的动力定位控制器设计*

王述桓1)徐海祥1,2)冯 辉2)余文曌2)

(武汉理工大学交通学院1)武汉 430063) (高性能船舶技术教育部重点实验室2)武汉 430063)

为实现动力定位系统定位及跟踪功能，设计了基于PID控制的反馈控制器.该控制器一方面简化了控制器的结构使得参数整定较为方便，另一方面通过使控制器的设定点沿着参考轨迹缓慢接近期望定位点避免了推力输出饱和情况.通过仿真实验，对比了提出的控制器与基于干扰补偿的反馈控制器的控制性能.仿真结果表明，该控制器具有参数易整定、鲁棒性强和控制性能好的优势.

动力定位；控制器；PID；定位；跟踪

0 引 言

动力定位系统(dynamic positioning,DP)中自动定位(auto positioning)模式的工作原理为：传感器系统测量船舶的运动状态信息及各种环境信息，状态估计滤波器通过这些信息估计出船舶的实际运动状态，然后控制器依据船舶当前时刻的运动状态计算使其到达设定运动状态所需的控制力并转化为控制指令，最后由推进系统执行控制指令完成船舶的定位及跟踪任务[1].

Balchen等[2]将卡尔曼(Kalman)滤波技术引入DP系统是为了解决在应用单输入单输出的PID控制器结合低通或陷波滤波时的相位滞后和积分饱和问题，同时应用现代控制理论中最优控制理论对船舶三自由度运动分别进行控制，忽略了船舶三自由度运动的耦合效应；Sørensen等[3]对该方法进行了进一步的完善；Katebi等[4]将H∞鲁棒控制方法应用到DP系统控制器的设计；Tannuri等[5]提出非线性滑模控制技术在DP系统中的应用.Fossen等[6]基于系统无源性理论提出一种无源非线性观测器对船舶运动状态进行实时估计，包括对未建模缓变环境力扰动项的估计.Loria等[7]在对无源非线性观测器与控制器构成的级联系统稳定性证明的基础上，推导出了满足全局指数稳定性的反馈控制律，该控制律为PD控制项加上干扰补偿项；Fossen等[8]在此基础上对DP系统中无源性理论的应用进行了进一步的完善和总结，通过船舶低频运动速度的积分对反馈控制律中的干扰项进行估计，但控制器中待整定参数较多.Nguyen等[9]设计监督系统对海况情况进行预测分析，通过切换逻辑选择合适的状态观测器和控制器，用以对不同海况下的船舶运动进行控制，但在恶劣海况下应用加速度反馈控制时加速度难以测量.Fannemel[10]将工业控制中的模型预测控制方法引入DP系统，并加入推力限制约束，通过多步预测及滚动优化得到每一时刻系统的最优输入，但对运算速度有较高要求.

针对动力定位系统中已有的控制算法中存在的问题，本文在保证控制算法收敛的前提下，采用了结构较为简单的PID控制方法，以系统惯性矩阵为依据来设计控制器参数，减少了待整定参数的数量；通过使控制器的设定点沿着参考轨迹缓慢接近期望定位点来避免推力输出饱和情况.最后，设计基于船模参数的仿真试验对设计的控制器进行验证，通过对比试验分析证明了该控制器的优势.

1 数学模型

1.1 参考坐标系

船舶动力定位系统一般只考虑纵荡、横荡和首摇三个自由度的水平运动.用到的参考坐标系系统为：①北东坐标系，或称为{n}-坐标系；②船体坐标系，或称为{b}-坐标系.

1.2 DP船舶数学模型

在低速情况下，船舶漂角β≈0，船舶航向角ψc≈ψ，ψ为船舶首向角.此时，动力定位船舶3自由度运动及动力学数学模型为

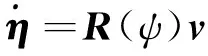
(1)

(2)

式中：η=[x,y,ψ]T为船舶重心在{n}-坐标系中的位置；v=[u,υ,r]T为船舶重心在{b}-坐标系中的速度；R(ψ)∈R3×3为{n}-坐标系与{b}-坐标系之间的旋转矩阵；M为船舶水动力系统的惯性矩阵；D为线性水动力阻尼矩阵；b为{n}-坐标系中作用于船体上的缓变扰动力，包含二阶波浪慢漂力、海流力和未建模的动态力；τwind为{b}-坐标系中作用于船体上的风力；τ为控制器输出的推力；-τF为风前馈力.

M、D和R(ψ)的形式如下.

(3)

(4)

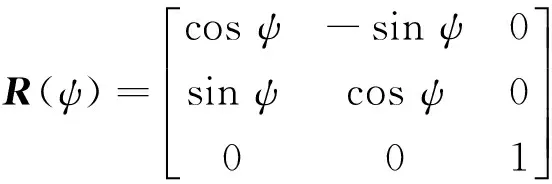
(5)

1.3 DP状态估计数学模型

DP状态估计是为了给出船舶运动状态和参数的最优估计，为控制器提供精确的输入，其数学模型为

(6)

ηw=Cwξ

(7)

(8)

(9)

(10)

y=η+ηw+υ

(11)

式中：ξ=[ξ1,ξ2]T∈R6×3,ξ1∈R3×3,ξ2∈R3×3；Aw,Ew,Cw均为系数矩阵；ηw=[xw,yw,ψw]T为船舶高频运动项；y∈R3×1为船舶测量位置；Tb∈R3×3为对角正定系数矩阵；式(2)中τwind项与-τF项抵消，若考虑不准确性噪声对模型的影响，即得到式(10)；w1,w2,w3∈R3×1均为零均值的高斯白噪声项；υ∈R3×1为测量白噪声向量.

矩阵Aw,Ew,Cw的形式如下.

(12)

(13)

Ω22=-diag{2ζ1ω01,2ζ2ω02,2ζ3ω03}

(14)

Σ2=diag{σ1,σ2,σ3}

(15)

式中：0为3×3的零矩阵；I为3×3的单位矩阵；ω0i(i=1,2,3)为波浪谱峰频率；ζi(i=1,2,3)为相对阻尼率；σi(i=1,2,3)与波浪强度相关.

2 离散型EKF的设计

由式(6)～(11)可得状态估计数学模型的状态空间形式为

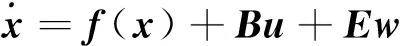
(16)

y=Hx+υ

(17)

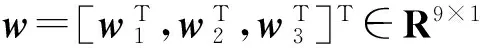
矩阵f(x),B,E,H的形式为

(18)

(19)

(20)

式(16)可写成如下一般形式

(21)

f(x,u)=f(x)+Bu

(22)

离散型EKF的设计过程如下.

1) 定义过程噪声协方差和测量噪声协方差的矩阵Q、R.

3) 计算Kalman增益并校正这一时刻的后验均方差和后验状态向量.

(23)

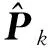
(25)

4) 预测下一时刻的先验均方差和先验状态向量.

(26)

(27)

(28)

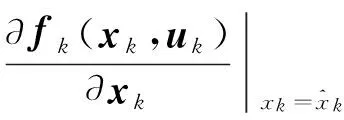
(29)

Gk=h·E

(30)

式中：h>0，为离散化步长.

3 控制器的设计

在DP船舶进行定位及跟踪过程中，控制器根据船舶当前位置点与设定点之间的偏差在满足一定控制性能的同时计算得到用于抵消偏差的推力；若t=0 s时刻定位点改变，为了避免船舶运动初期控制器中的偏差过大而导致输出推力饱和情况，使控制器的设定点沿着参考轨迹缓慢接近期望定位点，同时加入设定点位置及艏向值的上下限，即

ηd(t)=[xd(t),yd(t),ψd(t)]T

(31)

xd(t)=rt2(m)

(32)

(33)

(34)

(35)

(36)

(37)

式中：t为时间；ηd(t)为{n}-坐标系中控制器的设定点位置；ηdt=[xdt,ydt,ψdt]T为{n}-坐标系中期望定位点的位置；r为实常数.

控制器C1表示文中提出的控制器，即

(38)

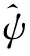
(40)

(41)

Kd=k3·M

(42)

(43)

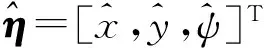
控制器C2表示用于对比实验的控制器，即

(44)

(45)

(46)

(47)

根据以上过程可知，控制器C1中待整定参数有4个，且PID参数整定有规律可循；而控制器C2中待整定参数有6个，且系数矩阵Γ中的参数难以抉择.

4 仿真实验

在Matlab上进行仿真试验，仿真试验中用到的M，D参数来自于本实验室一艘供应船的缩尺比船模.该模型艉部装有两个全回转推进器，艏部装有两个槽道推进器，每个全回转推进器的推力上限为49 N，每个槽道推进器的推力上限为14 N.

为了验证文中设计的控制器的性能，将状态估计、控制器和推力分配组成一个闭环系统.状态估计采用扩展卡尔曼滤波，推力分配中加入推力变化率的约束来避免输出推力大小的剧烈变化.

M，D根据式(3)～(4)代入水动力导数计算得到，质量单位为kg，长度单位为m，为

高频运动模型中波浪参数的选取为

ω0i=0.8 rad/s (i=1,2,3)

ζi=0.1 (i=1,2,3)

σi=0.8,0.6,0.5 (i=1,2,3)

缓变扰动力模型中参数的选取为

扩展卡尔曼滤波器中的过程噪声协方差矩阵为对角矩阵，对角线上的元素取为0.1,0.1,0.1,0.01,0.01,0.01,0.01,0.01,0.01；测量噪声协方差矩阵为对角矩阵，对角线上的元素取为0.2,0.2,0.05；初始先验均方差矩阵为对角矩阵，对角线上的元素取为0.1,0.1,0.1,0.2,0.1,0.1,0.2,0.3,0.1；初始先验状态向量取为15×1的零矩阵；离散化步长取为h=0.3.

船舶动力学数学模型中加入的未建模缓变扰动力为

b=[2 N,2 N,1 N·m]T.

控制器C1中参数经整定后的选取为：

k1=0.043,k2=0.001,k3=2.2,r=0.001.

控制器C2中参数经整定后的选取为

r=0.001.

加入推力变化率的约束为

式中：τx,τy分别为控制器输出的纵荡、横荡推力，N；τz为首摇方向的力矩，N·m.

仿真周期T=0.5 s，仿真时长为1 000个周期.设定船舶的初始定位点为η0=[0 m,0 m,0 rad]T，t=0 s时刻，船舶的定位点发生改变，期望定位点为ηdt=[5 m,5 m,π/3 rad]T.

为证明控制器C1的优势，设计了对比仿真实验，与之对比的对象是控制器C2.仿真结果见图1～4.

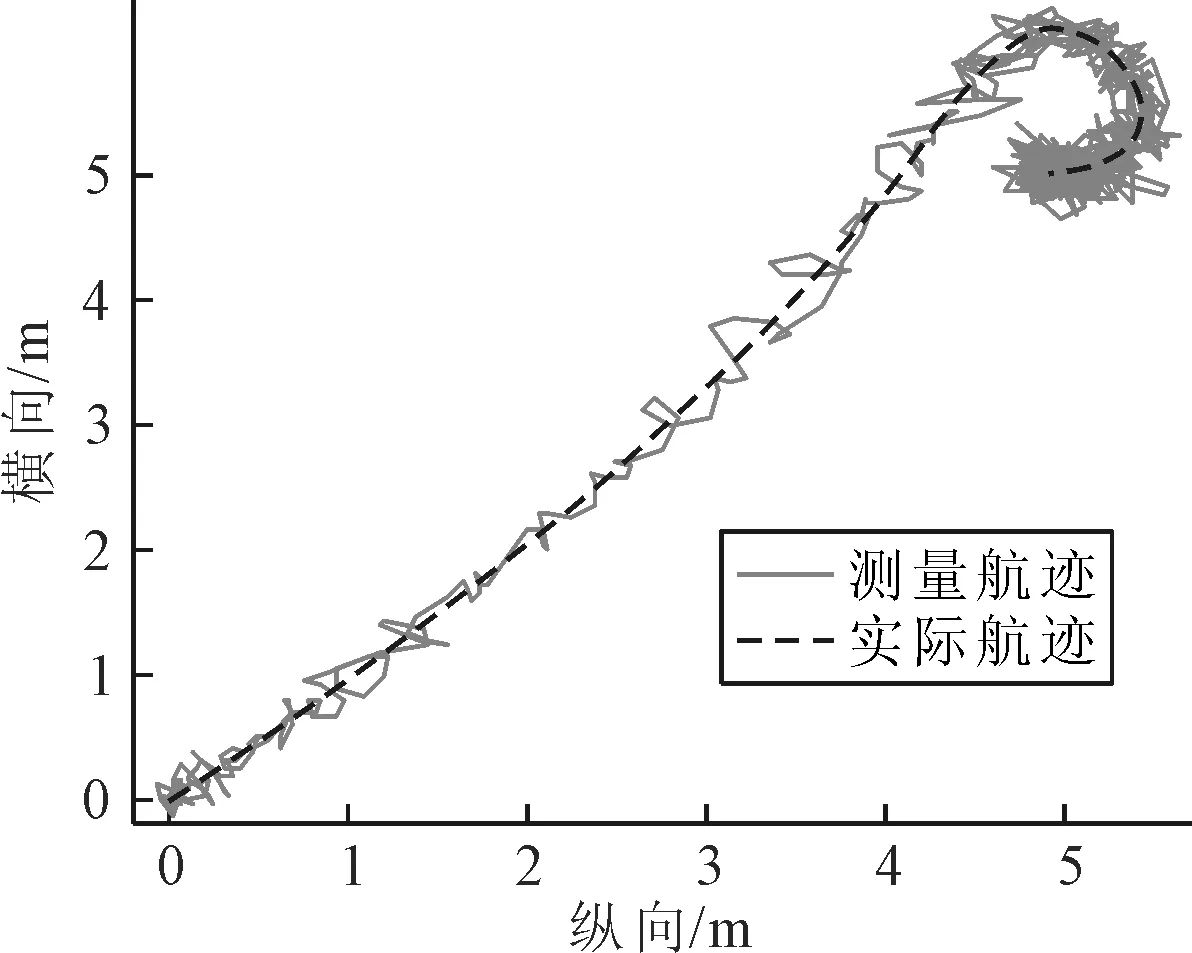
图1 控制器C1作用时船舶位置随时间的变化

由图1可知，仿真中船舶位置变化非常平缓，控制器对EKF观测器给出的低频估计运动进行了有效地控制，整个系统在噪声信号及固定干扰力影响下保持稳定.

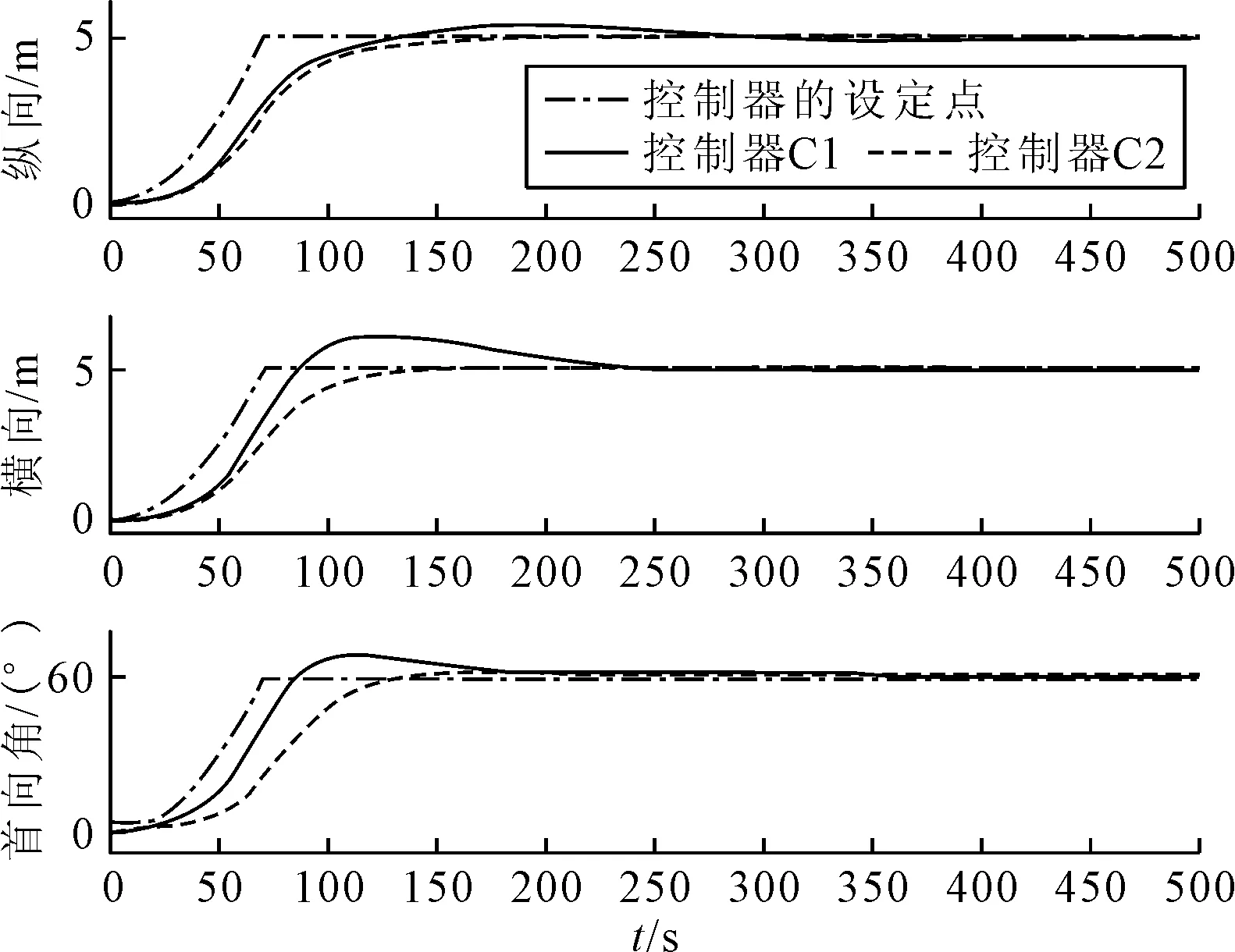
图2 船舶纵向、横向位置及首向角随时间的变化

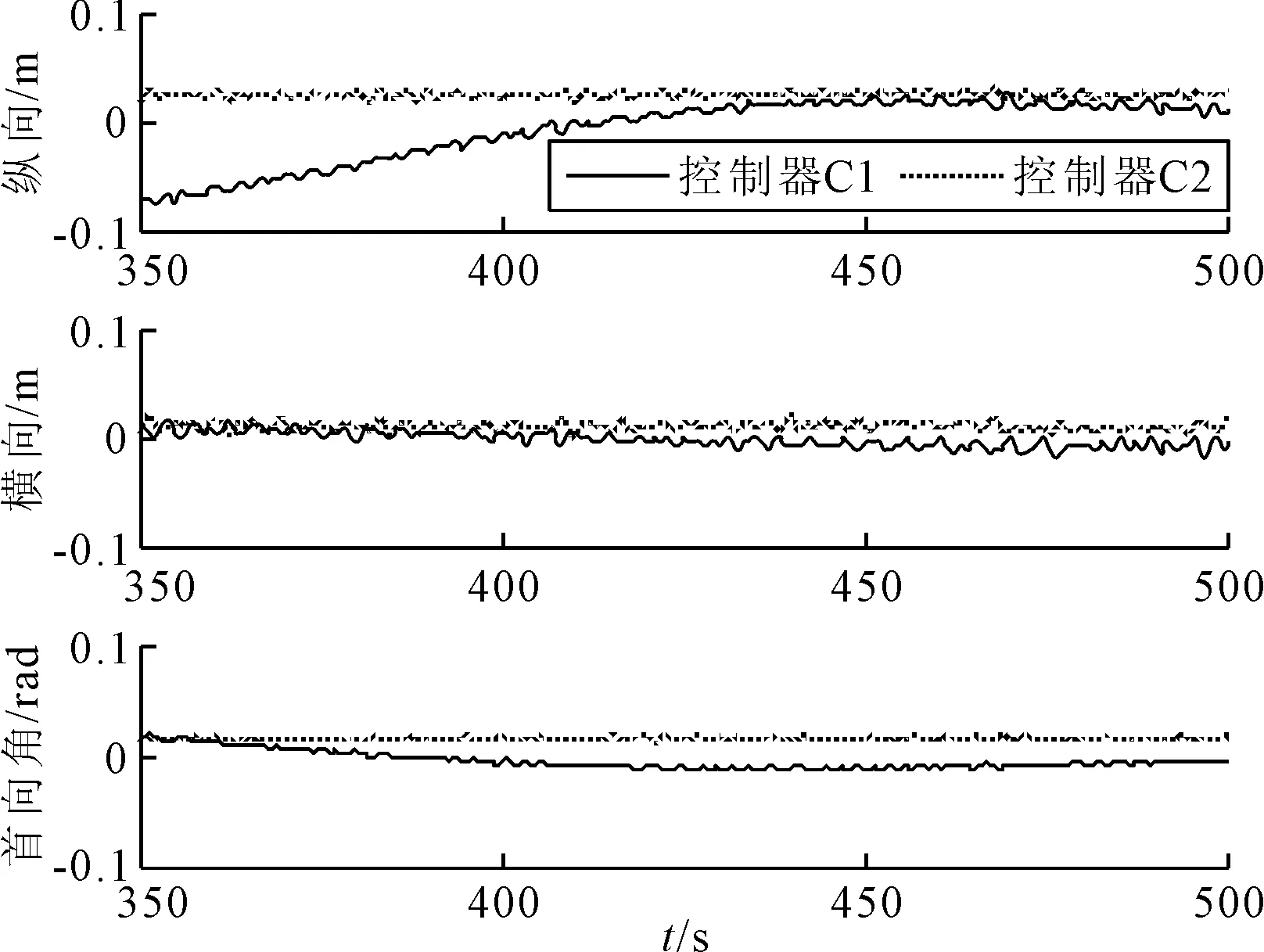
图3 船舶纵向、横向位置及首向角与期望值的偏差随时间的变化

由图2～3可知，当t=0 s时刻定位点改变，两种控制器都能使船舶跟踪到新的定位点，约200 s后，船舶位置及首向角最终保持稳定；控制器C1的定位精度较高，且首向最为明显.

图4 船体坐标系下船舶在定位及跟踪过程中纵荡、横荡和首摇方向的推力和力矩随时间的变化

由图4可知，两种控制器输出的推力指令中纵荡和横荡方向的推力均不超过5 N，首摇方向的力矩值均不超过10 N·m，根据该船模的推进器配置及推力上限可知，不会出现推力输出饱和情况；在50～100 s时间段内，即船舶在跟踪期望定位点的过程中，控制器C1输出的横荡和首摇方向的推力和力矩变化相对平缓.

5 结 束 语

文中设计了用于定位及跟踪功能的DP系统控制器，使控制器的设定点沿着参考轨迹缓慢接近期望定位点来避免推力输出饱和情况.采用了结构较为简单的PID控制方法来设计控制器，并以船模质量矩阵为依据来设计控制器参数，既保证了控制效果，又方便了参数整定.控制器对EKF观测器给出的低频估计运动进行了有效地控制，且整个系统在加入噪声信号后保持稳定；当加入较为严格的推力变化率约束后，控制算法收敛且控制器输出的推力没有出现剧烈变化.船舶动力学模型中加入固定的未建模干扰力后控制器能达到预定的控制效果.

[1]徐海祥，冯辉.船舶动力定位系统原理[M].北京：国防工业出版社，2016.

[2]BALCHEN J G, JENSSEN N A, MATHISEN E, et al. A dynamic positioning system based on Kalman filtering and optimal control[J]. Modeling Identification and Control,1980,1(3):135-163.

[3]SØRENSEN A J, SAGATUN S I, FOSSEN T I. Design of a dynamic positioning system using model-based control[J]. Control Engineering Practice,1996,4(3):359-368.

[4]KATEBI M R, GRIMBLE M J, ZHANG Y.H∞ro-bust control design for dynamic ship positioning[J]. IEE Proceedings Control Theory and Applications,1997,144:110-120.

[5]TANNURI E A, DONHA D C, PESCE C P. Dynamic positioning of a turret moored FPSO using sliding mode control[J]. International Journal of Robust and Nonlinear Control,2001,11(13):1239-1256.

[6]FOSSEN T I, STRAND J P. Passive nonlinear observer design for ships using Lyapunov methods: full-scale experiments with a supply vessel[J]. Automatica,1999,35(1):3-16.

[7]LORIA A, FOSSEN T I, PANTELEY E. A separation principle for dynamic positioning of ships: theoretical and experimental results[J]. IEEE Transaction on Control System Technology,2000,8(2):332-343.

[8]FOSSEN T I. Nonlinear passive control and observer design for ships[J]. Modeling, Identification and Control,2000,21(3):129-184.

[9]NGUYEN T D, SORENSEN A J, QUEK S T. Design of hybrid controller for dynamic positioning from calm to extreme sea conditions[J]. Automatica,2007,43(5):768-785.

[10]FANNEMEL V. Dynamic positioning by nonlinear model predictive control[D]. Teknisk Kybernetikk: Institutt for Teknisk Kybernetikk,2008.

Design of the Controller for Dynamic Positioning Based on Trajectory Tracking

WANG Shuhuan1)XU Haixiang1,2)FENG Hui2)YU Wenzhao2)

(School of Transportation, Wuhan University of Technology, Wuhan 430063, China)1)(Key Laboratory of High Performance Ship Technology of Ministry of Education, Wuhan 430063, China)2)

In order to achieve the positioning and tracking functions of dynamic positioning system, a feedback controller based on PID is designed. On the one hand, the structure of the controller is simplified so that it is more convenient for parameter tuning. On the other hand, the thrust saturation condition is avoided by means of making the control set-point slowly approaching the desired anchor point. The control performances between the proposed controller and the feedback controller based on the bias compensation are compared by the simulation experiment. The results show that the proposed controller has the advantages of easier parameter tuning, higher robustness and better control performance.

dynamic positioning; controller; PID; station-keeping; tracking

2017-03-22

*国家自然科学基金项目(61301279, 51479158)、中央高校基本科研业务费专项资金项目(163102006)资助

U674.38

10.3963/j.issn.2095-3844.2017.03.022

王述桓(1993—)：男，硕士生，主要研究领域为船舶运动控制