改进粒子群算法在多目标物流选址中的应用*

龙圣杰 刘衍民 曾庆雨

(遵义师范学院数学学院 遵义 563002)

改进粒子群算法在多目标物流选址中的应用*

龙圣杰 刘衍民 曾庆雨

(遵义师范学院数学学院 遵义 563002)

考虑到物流选址规划对系统运营的影响，以物流运营成本最小及服务满意度最大为目标，构建工厂-物流中心-分销商三级物流选址规划模型.为了避免粒子群算法容易早熟和容易落入局部最优的缺陷，引入合作学习思想，针对多目标选址规划问题，用多目标合作粒子群算法(MCPSO)求多目标离散型物流选址规划模型的Pareto解.通过对实例进行仿真模拟，求解模型的选址-分派方案，并结合灵敏度分析，证明所提出算法的有效性.

物流选址规划；多目标；合作学习；粒子群算法；仿真

0 引 言

全球化市场竞争环境下，整个价值链的竞争能力替代了以往强调企业个体竞争能力，实现成本最低与服务最大化一直是产品价值链的核心问题[1].物流规划中的选址与其分派计划的制定密切相关，因此物流中心研究的核心在于选址规划问题[2].国内外很多学者建立了一系列的模型与算法针对这一问题进行了定性与定量的研究[3-4].对于选址规划问题，按照模型与优化算法的不同可分为连续型与离散型[5-6].物流规划涉及的多目标问题，大多数研究以权重法将多目标优化模型转化为单目标优化，或是采用目标规划法将主要目标以外的目标函数转化为约束条件[7].物流中心选址规划这类涉及的成本与服务等存在背反效应的多个目标，以上提到的方法依赖于主观性或是牺牲其他目标函数的方法对于多目标寻优具有很大限制[8]，因此，提出构建离散型多目标物流规划模型寻求Pareto解.

对于物流规划问题研究涉及的多目标、多维度解的问题，采用常规方法运算量大、计算复杂程度高，而当前的一些启发式方法容易陷入局部最优[9].针对多目标物流规划的NP-hard问题，为克服传统的粒子群算法容易陷入局部最优的情况，学者们提出了对粒子群的改进：①对粒子群算法惯性参数进行调整，包括动态策略和自适应方法，学习因子和社会因子的调整[10]；②提出邻域搜索策略，加强当前种群邻域的勘探[11]；③粒子群采用信息共享机制，增强种群多样性而避免算法早熟；④与其他算法相融合，如粒子群优化算法与免疫算法、遗传算法、人工蜂群算法的结合[12].离散型问题中，解的每一个维度都对应一个寻优方案，向单一gbest粒子学习的策略容易忽略解空间的一些优秀‘单元’，同时也容易丧失粒子多样性而迅速陷入局部最优.针对离散型物流规划模型解空间存在多目标、多维度的特点，采用粒子不同维度向解空间其他优秀粒子合作学习的方式，构建合作学习粒子群算法对多目标离散型物流规划问题进行寻优求解.

1 多目标物流规划模型构建

1.1 基于客户满意度与服务成的物流中心选址模型描述

选择由I个工厂、J个物流中心和K个客户组成的典型三级物流网络进行选址研究.该物流网络服务于单一产品，其物流方式是工厂先将各自生产的货品运输到物流中心，再经过物流中心集中配货后运送给不同客户.工厂Fi(i=1,2,…,I)产量充足，客户Ck(k=1,2,…,K)的需求确定，备选物流中心Dj(j=1,2,…,J)为联系工厂与客户的中间节点.假设为了便于管理，在该物流网络中一个工厂只向一个物流中心供货，一个客户也只接受一个物流中心的服务.此时，物流网络的规划就涉及两个问题:

1) 物流中心的选址 在J个备选物流中心中选择若干个建设并使用.

2) 物流分派的制定 分别确定为每个工厂Fi与客户Ck服务的物流中心Dj.

1.2 客户满意度函数

时效性是衡量物流系统的一个重要指标，它反映了物流系统为客户提供物流服务的能力，也体现了该物流系统的市场竞争力.物流中心Dj在客户Ck要求的时间内满足其物流服务的概率表达式为

Pij=P(tij≤ti)=

(1)

式中：Tij为产品由物流中心i到客户j的运输时间；dij为产品由物流中心i到客户j的运输距离；vij为产品由物流中心i到客户j的运输速度；ti为客户要求的最大运输时间；Fvij(*)为运输车辆由物流中心i到客户j的速度分布函数.

定义Pij为客户j对物流中心i提供的物流服务满意度，由若干个物流中心与若干个客户组成的物流系统的总体物流服务满意度为

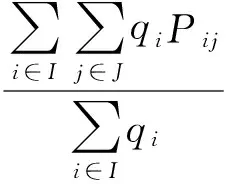
(2)

式中：Ps为物流系统总体服务满意度；qi为客户i的产品需求量.

1.3 多目标物流选址模型数学表达式

物流选址-分派模型的目的是实现总成本最小及服务满意度最高.建立的多目标物流选址模型为

maxTs(φij,φjk)=

(3)

(4)

s.t.

(5)

(6)

(7)

(8)

φj=0,1,j∈J

(9)

φij=0,1,i∈I,j∈J

(10)

φjk=0,1,j∈J,k∈K

(11)

式中：Fvijk(*)为车辆从工厂i经过物流中心j到达客户k的速度分布函数，服从正态分布；Qj为备选物流中心j的物流容量；Qk为客户k的产品需求量；φi为0-1变量，选择物流中心j则为1，否则为0；φij为0-1变量，产品由工厂i经过物流中心j为1，否则为0；φjk为0-1变量，产品由物流中心j送达客户k则为1，否则为0；cij为工厂i到物流中心j单位运输费用；cjk为物流中心j到客户k单位运输费用；dij为工厂i到物流中心j的距离；djk为物流中心j到客户k的距离；tk为客户k要求的物流时间；xij为由工厂i送达物流中心j的产品量；xjk为物流中心j送达客户k的产品量.

Ts(φij，φjk)为物流系统服务满意度目标函数，运用到1.2中介绍到的计算方式；Tc(φi，φij，φjk)为物流系统成本目标函数，包括物流中心建设成本、工厂到物流中心的运输成本和物流中心到客户的运输成本；约束条件表示每个客户只由一个物流中心提供服务.

当存在一组解间不存在Pareto支配时，讲其称为多目标规划的Pareto解.多目标函数处于冲突状态时，不存在使得所有目标函数同时达到最大或者最小值的最优解，此时我们只能寻求Pareto解.

2 粒子群算法编码及改进

粒子群算法(PSO)是1995年由Kennedy和Eberhart提出的一种进化计算技术，源于对鸟群和鱼群捕食等行为的模拟.目前，PSO及其改进算法已广泛应用于函数优化、神经网络训练、模糊系统控制、模式识别及工程应用等诸多领域，并被证明能够以较小的计算代价获得良好的优化解.其核心内容为参数编码、初始群体设计、适应度函数设计、进化操作设计与参数控制五部分.

2.1 粒子群优化算法

算法中粒子有n个参数，种群包括m个粒子，第i个粒子演化到k代为xik={xi1k，xi2k,…,ximk}，i=1,2,…,m.根据算法适应度函数，计算出粒子当前最优位置为pik={pi1k，pi2k,…,pimk}，以及群体最优适应值，第i粒子下一步迭代速度与位置计算公式为

(12)

(13)

式中：i=1,2,…,m；j=1,2,…,n；s1为粒子自我认知学习系数；s2为粒子社会认知学习系数；r1，r2为(0,1)分布的随机数;w为粒子变化惯性权重，它决定了粒子先前速度对当前速度的影响程度.

2.2 粒子群编码设计

选址规划模型中，有两种粒子：位置粒子A与B、速度粒子VA与VB，其中粒子A与VA为J维，粒子B与VB为K维的浮点数(以典型三级物流网络为例，假设模型中有I个工厂、J个备选物流中心和K个客户).采用整数编码形式，物流中心粒子的位数与备选物流中心的位数相对应.将J个备选物流中心按照I～J依次编号，物流中心粒子群第i个粒子演化到第t代时为Ai(t)={Ai1(t)，Ai2(t),…,Aiφ(t),…,AiJ(t)}.若粒子中Aiφ(t)位数值为n，则该位置为第n个被选中的物流中心，若该位置为0，则表示该位置的物流中心未被选中.

客户粒子B按照I～K依次编号，第i个粒子演化到第t代为Bi(t)={Bi1(t)，Bi2(t),…,Biφ(t),…,BiK(t)}.

若Biφ(t)为n,则该客户由选择建立的第n号物流中心提供服务.

例如，在4个备选物流中心中选择2个为4个分销商进行服务时，物流中心选址、分派粒子A，B离散化后分别为

A={1，0，3,0}，B={1,3,1,3}

表示1号与3号备选物流中心被选中.其中1号物流中心为1,3号客户服务，3号物流中心为2,4号客户服务.此时A，B粒子对应的物流配送网络结构图见图1.

图1 物流选址规划结构图

2.3 算法改进及设计

经典粒子群算法中粒子分别向代表“认知部分”的pi(t)与“社会部分”pg(t)学习，由于组合优化问题解空间中每个维度都是的一个解中的元素，“社会部分”单纯向一个pg(t)学习很有可能错过粒子某一维度的最优解，导致“two steps forward,one step back”的现象.

提出的合作学习的方式对粒子群算法进行改进，该算法粒子“社会部分”不是向g(t)学习，而是粒子每一个维度d以一定的概率向粒子群中具有优秀适应度值的粒子学习.在该算法中，速度更新公式为

(14)

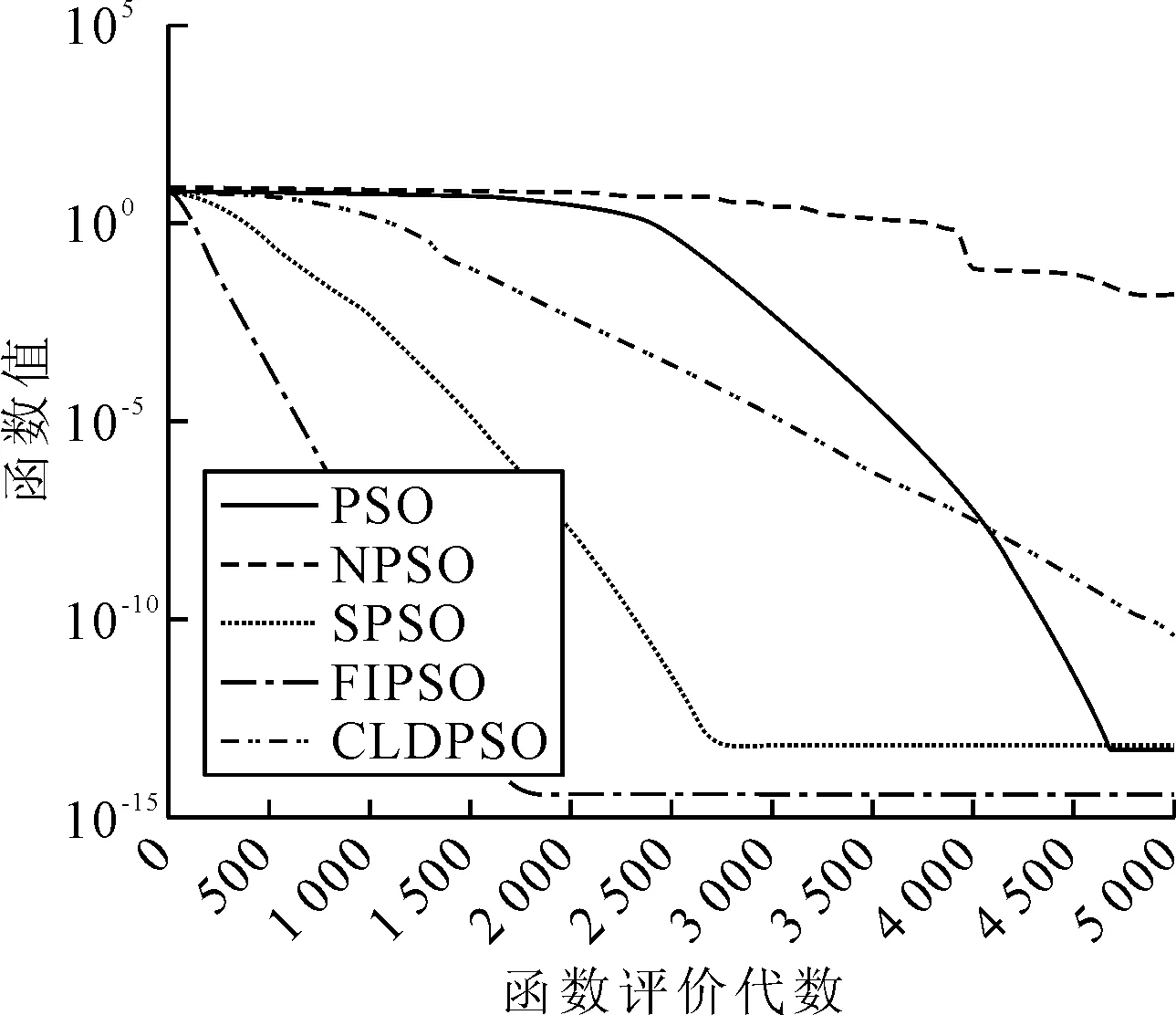
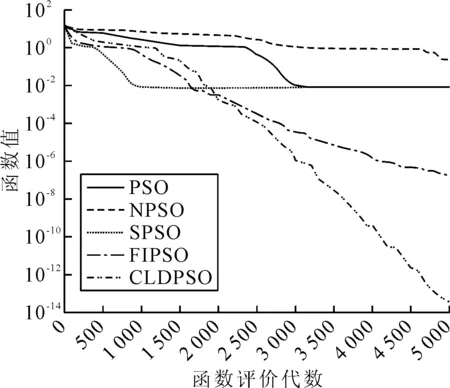
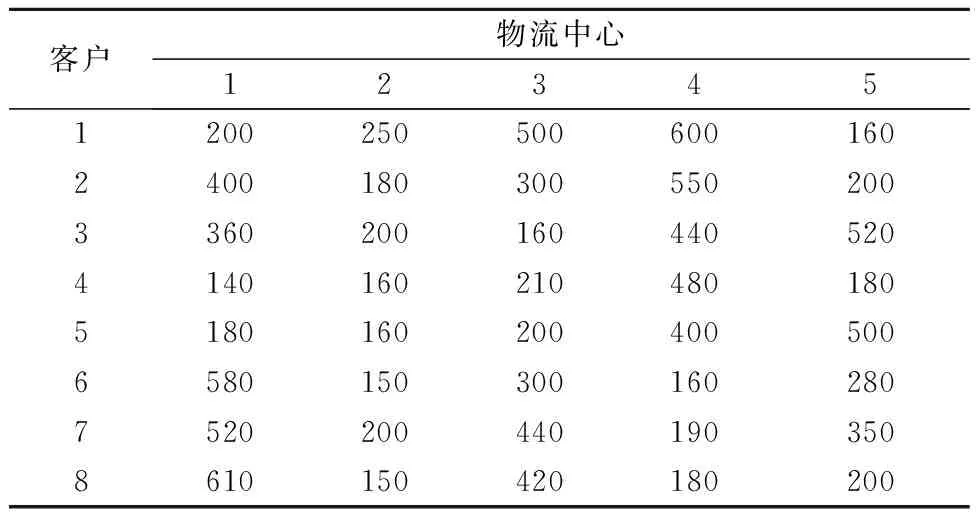
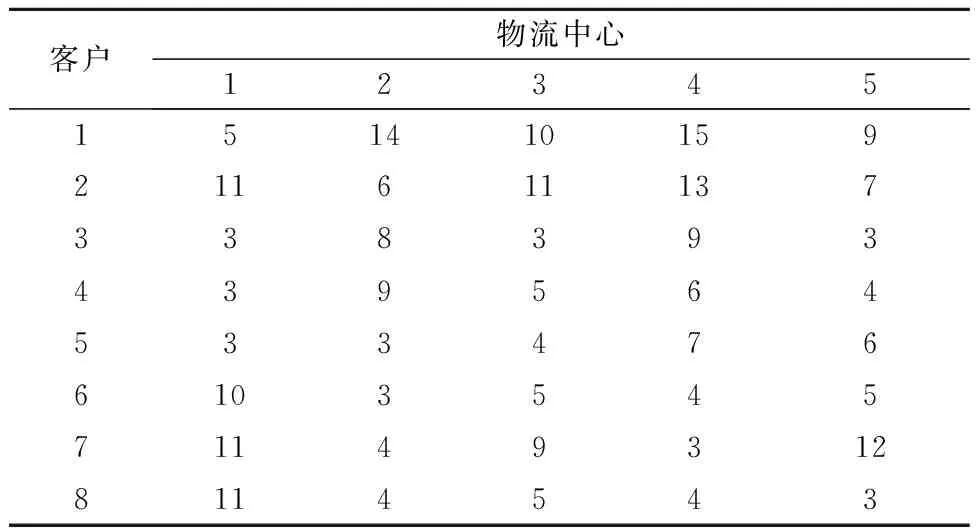
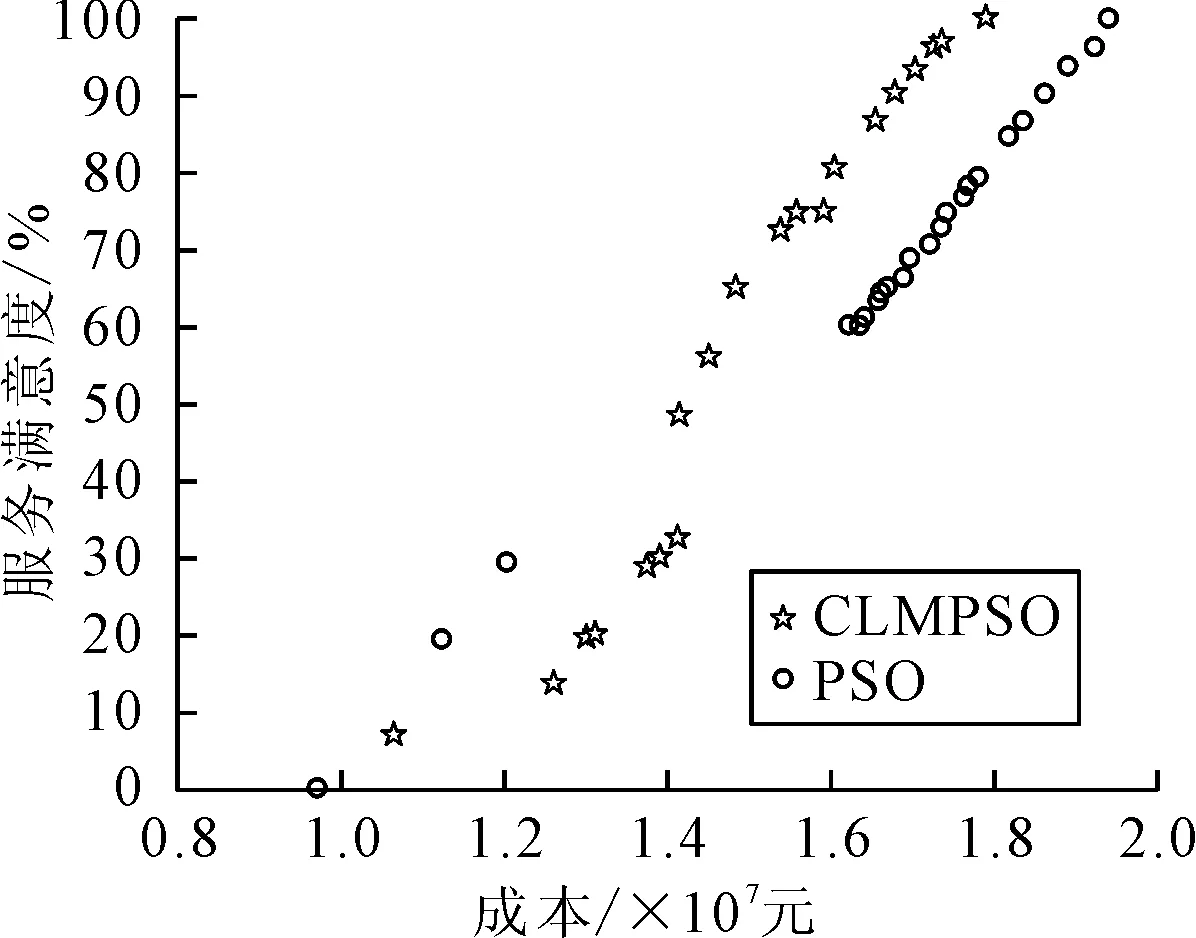
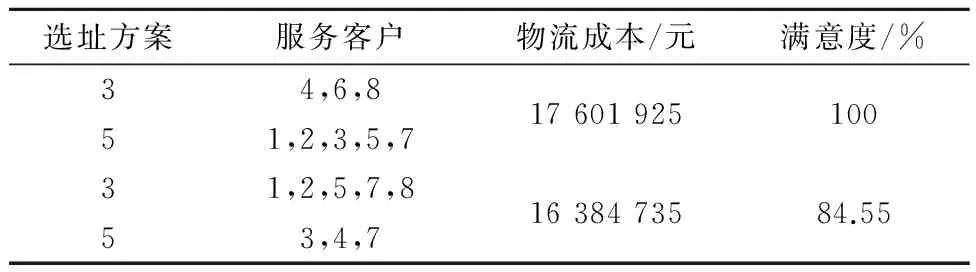
式中：pdf(i)(t)为i粒子d维度学习的对象，为了保证粒子的多样性学习对象也包括自身的pdi(t).对于粒子i的任意维度d，产生一个随机数，如果该随机数大于Pc则粒子i的d维度向自身的pdi(t)学习，如该随机数小于Pc则粒子i的d维度则向pdf(i)(t)学习.在合作学习的多目标粒子群算法(CLMPSO)选择学习粒子的方法为：①在粒子群中随机选择n个粒子；②以(Tc(i)>Tc(j))&&(Ts(i)Tc(j))&&(abs(Ts(i)-Ts(j))

与经典的PSO比较，提出的MCPOS采用粒子的不同维度分别向非劣解对应粒子的学习的策略，该方法操作简单，计算复杂度小.采用向非劣解粒子学习的方式可以避免PSO算法存在的向gbest快速收敛的趋势，扩展粒子的多样性而避免收敛到局部最优解,见图2.针对不同维度的学习方式，尤其适合于存在众多局部最优的离散型问题求解.

图2 PSO与MCPSO搜寻范围图

在传统的PSO中，全局最优gbest粒子与粒子历史最优pbest粒子决定了粒子的速度与搜索范围.当gbest粒子与pbest粒子同时陷入局部最优区域时，粒子很容易收敛到局部最优解，见图2b).然而文中提出的MCPOS中，粒子的各个维度分别向整个解空间中非劣解粒子学习，能够扩展了粒子搜寻范围，增加跳出局部最优的可能性.

具体算法为：①初始化粒子的位置与速度，并设定粒子学习概率；②Whilei≤pSize，确定i粒子的维度d学习对象；③Whiled≤D，随机选择种群中的n个粒子，计算出对应粒子的物流成本与服务满意度，并筛选出多目标非劣解；④随机选择非劣解粒子作为i粒子的维度d学习对象，更新粒子i各个维度的速度；⑤更新粒子群的位置；⑥判断是否达到结束条件，如果没有转到步骤②，否则结束.

3 仿真实验与算例分析

3.1 收敛特性仿真实验

文中为了评估MCPOS运行效率，设计了一个类比实验，比较本文的MCPOS算法与标准PSO算法、加入收缩因子的PSO算法(SPSO)，邻域学习PSO(NPSO)，完全信息PSO算法(FIPSO-square)进行比较.引入3个常使用的Benchmark函数进行数值实验，函数Sphere与Rosenbrock是连续单模态函数，Rastrigin与Griewank是典型的非线性多模态函数，二者具有广泛的搜索空间，大量的局部最优点和众多寻优障碍.表1为benchmark函数的定义和全局最优解.实验种群规模为30，函数维度为30，搜索范围分别为：(-100,100)，(-2.048，2.048)，(-5.12,5.12)，(-600,600)，函数每次运行5 000代.

图3～4为各种PSO处理单峰Benchmark函数的结果，由图3～4可知，在单峰Benchmark函数中，经典PSO与SPSO算法收敛速度快、效果相对较好，MCPOS与其他算法在搜索前期都有一个下降的趋势，5 000代的计算中与其他算法相比较优势并不明显.图5～6为多峰问题Rastrigin与Griewank函数的结果.由图5～6可知，文中提出的算法具有明显优势.这正是由于算法中粒子的各个维度采用了向不同粒子全面学习的策略，增加了粒子多样性，从而增强跳出局部最优的能力.

表1 Benchmark函数

图3 30维Sphere函数收敛图

图4 30维Rosenbrock函数收敛图

图5 30维Rastrigin函数收敛图

图6 30维Griewank函数收敛图

4 CLMPSO在离散型物流选址中的应用

4.1 模型相关参数

模型由1个工厂(I=1)、5个候选物流配送中心(J=5)与8个顾客需求点(K=8)组成.假设每备选物流中心建设成本都为1 000万元，最大转运量都为1 500 t.运输产品的车辆的行驶速度服从均值为40 km/h、方差为10的正态分布，客户要求配送时限都为8 h.其他相关数据见表2～7.

表2 客户的需求期望值 t

表3 各个备选物流中心的处理费用 元/t

表4 工厂与备选物流中心的距离 km

表5 工厂与备选物流中心的单位运输费用t·km/元

表6 备选物流中心与客户的距离 km

4.2 选址规划模型求解结果及分析

基于多目标粒子群算法的参数分别为：粒子种规模pSize=1 000；算法开始迭代惯性权重Wstart=0.95；算法开始迭代惯性权重Wend=0.4；PSO粒子自我认知加速系数c1=2；PSO粒子社会认知加速系数c2=2；MCPOS粒子社会学习概率Pc=0.5.

表7 备选物流中心与客户的单位配送费用t·km/元

根据上述模型与算法进行求解，经过迭代能够获得稳定的perato解，运算记录的选址规划方案的多目标非劣解见图7.

图7 多目标选址规划实验统计图

由图7可知，相对于传统的PSO,采用合作学习的PSO在计算多目标物流选址问题时，在同样的成本下能够获得服务满意度更高寻优结果.由于多目标离散型物流选址规划属于多峰值的NP-hard问题，传统PSO粒子寻优过程中很容易陷入局部最优，在相同的服务满意度下，获得的最优解花费的成本高于MCPOS.

采用MCPOS计算不同的物流规划策略对其成本和服务满意也会有所不同，表8为算法计算的其中两种物流规划方案.

表8 物流中心规划模型计算结果

5 结 束 语

提出MCPOS解决物流选址规划问题，从合作学习的角度对此类多目标离散型组合优化问题提出解决方案，提出粒子的各个维度向不同的非劣解粒子进行学习，对于跳出局部最优解具有很好的效果.与传统的PSO相比，该算法增加了粒子多样性，提高了解空间粒子的质量，能够在满足物流系统中客户满意度的前提下减少物流配送的距离及成本，从而提升物流的竞争力.

该算法采用在非劣解粒子中随机选择的方式，需要较长的计算时间和较大的收敛代数，因此采用何种粒子择优学习有待进一步研究.

[1]杜丽敬,李延晖.选址-库存-路径问题模型及其集成优化算法[J].运筹与管理,2014(4):70-79.

[3]KUO M S. Optimal location selection for an international distribution center by using a new hybrid method[J]．Expert Systems with Applications,2011,38(6):720-724．

[4]PRODHON C, PRINS C. A survey of recent research on location-routing problems[J]. European Journal of Operational Research,2014,238(1):1-17.

[5]CAI Q, GONG M, MA L, et al. Greedy discrete particle swarm optimization for large-scale social network clustering[J]. Information Sciences,2015,316(41):503-516.

[6]EKSIOGLUA B, VURALB A V, REISMANC A. The vehicle routing problem: a taxonomic review[J]．Computers & Industrial Engineering，2009，57(4)：147-148．

[7]涂南,戴雯婧,麦合迪.基于进化算法的多目标闭环物流网络设计[J].工业工程,2013,16(2):59-66.

[8]WANG N, LU J C, KVAM P. Reliability modeling in spatially distributed logistics systems[J]. Reliability, IEEE Transactions on,2006,55(3):525-534.

[9]胡丹丹,杨超,杨珺.设施数目不确定情况下的截流选址问题[J].工业工程与管理,2009,14(1):15-18.

[10]HAN W, YANG R H. Comparison study of several kinds of inertia weights for PSO[C]. Proc of 2010 IEEE IntConf on Informatics and Computing,Shanghai,2010.

[11]CHENG X U, HE X U, SUN L, et al. Feature selection for cancer classification based on neighborhood rough set and particle swarm optimization[J]. Journal of Chinese Computer Systems,2014,35(11)：252-258．

[12]THANGARAJ R, PANT M, ABRAHAM A, et al. Particle swarnq optimization: hybridization perspectives and experimental illustrations[J]．Applied Mathematics and Computation，2011,217(12)：520-525.

The Application on Multi-objective Logistics Location Based on Improved PSO

LONG Shengjie LIU Yanmin ZENGO Qingyu

(Zunyi Normal College, College of mathematics, Zunyi 563002, China)

Considering that the location of logistics center has great influence on the capacity of the logistics system, the logistics cost and logistics service capacity must therefore be considered when building a logistics location-allocation model. For the multi-objective location-allocation problem on logistics, this paper proposes a cooperative learning multi-objective particle swarm optimization algorithm of seeking for Perato dominant. The simulation result shows that the model is correct and effective, and the discrete multi-objective particle swarm optimization algorithm can effectively solve the multi-objective location-allocation problem.

logistics location; multi-objective optimization; Cooperative learning; particle swarm optimization; simulation

2017-03-29

*国家自然科学基金项目(71461027)、贵州省自然科学基金项目(KY[2014]295)、贵州省科技厅联合基金项目(LH[2016]7028)、贵州省科技厅联合基金项目(LH[2016]7029)、贵州省科学技术基金(LH[2015]7050)资助

TP301.4

10.3963/j.issn.2095-3844.2017.03.002

龙圣杰(1988—)：男，硕士，讲师，主要研究领域为物流工程、系统仿真