直觉模糊Petri网的双向模糊故障推理算法*

孙晓玲

合肥师范学院 数学与统计学院，合肥 230601

直觉模糊Petri网的双向模糊故障推理算法*

孙晓玲+

合肥师范学院 数学与统计学院，合肥 230601

SUN Xiaoling.Bidirectional fuzzy fault reasoning algorithm of intuitionistic fuzzy Petri net.Journal of Frontiers of Computer Science and Technology,2017,11(6)：1006-1013.

针对故障诊断中故障现象与故障原因之间复杂的不确定关系，利用直觉模糊集表达不确定性信息的优势和Petri网的图形处理问题的能力，给出了基于直觉模糊Petri网的双向模糊故障推理算法。该算法首先利用反向直觉模糊推理算法对模型进行约减，查找故障原因，再利用正向直觉模糊推理算法对模型进行计算，输出结果。该算法既可将故障信息化繁为简，降低推理过程的时间复杂度，还能够使故障诊断的确定性程度得到进一步提高。汽车发动机诊断案例表明了所给双向直觉模糊推理算法的可行性和有效性。

直觉模糊Petri网；直觉模糊推理；故障诊断；双向模糊故障推理

1 引言

故障诊断是通过对系统相关的一些状态进行检测，保证故障发生时可以检测出与系统相关的特征信号。直觉模糊Petri网的一个重要应用就是进行故障诊断。在故障诊断中，使用的推理方法一般有正向推理和反向推理。正向推理是从事实到目标的推理，通常用于检测信息比较完备的在线故障检测和诊断问题。由于其推理过程是建立在整个知识库系统之上，推理前并不清楚哪些事实和推理规则与推理目标相关，只能从大范围的事实出发进行推理，势必会造成冗余计算。

反向模糊推理能够较好地解决上述的正向推理存在的问题，它是由结果到原因的推理方法，经常用于信息不太充分的离线故障诊断，其优势在于能够简化不必要的推理过程。例如文献[1]采用反向推理方法，将与问题有关的一部分产生式规则从知识库系统中分离出来进行推理计算，不但满足了实时性要求，还降低了冗余计算。

若能将正反向推理相结合，先进行正向推理寻找可能产生的故障，对这些可能故障采取预防措施加以防范，变“被动维修”为“主动维护”，一旦发现故障，再利用反向推理寻找故障源。若正反向推理结论相符，则说明诊断推理有效，若结论不相符，则需要不断调整库所和变迁的可信度、阈值或权值，直到两者结论相符为止。例如文献[2]提出将正反向推理相结合，并给出相应的诊断推理算法，实用性较强。

针对故障诊断中存在的不确定性信息的问题，文献[3]通过改进的模糊Petri网算法有效地解决了故障诊断过程中不确定性知识的模糊推理，通过引入虚库所和虚变迁概念解决了变迁是否触发以及最后故障事件模糊值的确定问题。文献[4]将模糊Petri网应用于高速铁路牵引供电系统故障诊断，能够在不确定或信息缺失的情况下，提高故障区域判断确定性。

本文在已有模糊Petri网正反向推理算法的基础上提出了基于直觉模糊Petri网的双向并行推理算法。将正向推理与反向推理结合在一起，构成正反向混合推理。先根据目标征兆利用反向推理推理出有可能会产生的故障，再利用正向推理验证故障。矩阵命令可作为正反向推理的基础，先利用逆向推理算法压缩矩阵的维数，再利用正向推理算法得到精简后的推理模型目标库所的标识值，最后通过实际推理算例验证双向推理算法的正确性及可行性。与已有直觉模糊推理算法相比，本文给出的正反向直觉模糊推理算法能够减少后向推理查询或检查的次数，有效缩小搜索空间，避免算法中出现的冗余，在提高大型知识库处理效率时优势尤为明显。

2 直觉模糊集合

模糊集合是描述不确定性知识的良好工具，而直觉模糊集合（intuitionistic fuzzy sets，IFS）增加了一个新的属性参数——非隶属度函数，因此比模糊集合在描述不确定性和模糊性知识方面更具实用性和灵活性。近几年，将直觉模糊集用于知识表示和模糊推理已成为新的研究热点[5-9]。文献[7]提出了新的直觉模糊集的相似度和模糊熵的定义，并验证了其有效性。文献[7]还对Atanassov所提出的直觉模糊集理论进行了改进和扩展，从而丰富了直觉模糊集理论。其中的直觉模糊集的定义如下。

定义1（直觉模糊数）若X为论域，则论域X上的直觉模糊集为：

其中，μA(x):X→[0,1]和γA(x):X→[0,1]分别是集合A的隶属度函数和非隶属度函数。对集合A上的任一元素x∈X，有0≤μA(x)+γA(x)≤1。(μA(x),γA(x))称作论域X上的直觉模糊数[7]。

根据定义1，传统模糊集也可表示成直觉模糊集{|x∈X}。

定义2（直觉指数）称πA=1-μA(x)-γA(x)为论域X上直觉模糊集A中元素x的直觉指数，它反映了元素x属于直觉模糊集A的犹豫程度或不确定程度。显然，对任一x∈X，有0≤πA(x)≤1。若B为X中的任一传统模糊集，则有元素x属于模糊集B的犹豫程度为：

由此可知，模糊集是直觉模糊集的特例[6]。

定义3[7-9]（直觉模糊集运算法则）若X为论域，A、B均为论域X上的直觉模糊集，则对任一x∈X，有以下运算法则：

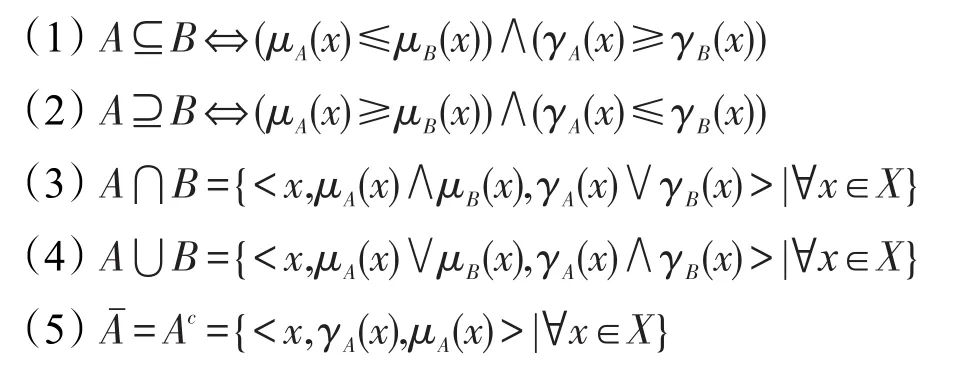
3 直觉模糊Petri网模型及相关运算符

直觉模糊Petri网（intuitionistic fuzzy Petri nets，IFPN）中通常有起始库所、中间库所和目标库所3类库所，起始库所表示故障征兆原因，目标库所表示征兆，其余称为中间库所。故障诊断的主要任务就是根据目标库所寻找导致目标库所的起始库所的过程。

根据模糊Petri网的推理特点可以分为多种推理方法，主要包括正向推理、反向推理、正反向混合推理和极大代数矩阵形式化推理。

3.1 直觉模糊Petri网模型

作为一种图形建模和分析工具，Petri网特别适合用来研究异步、并发特征的离散事件系统，被广泛运用于复杂系统的设计与分析中。但Petri网不能描述系统的模糊行为，因此研究者们提出了模糊Petri网的概念。

模糊Petri网是将Petri理论与模糊集合理论有机融合的新型网络理论，它既具有Petri网的图形描述能力，又具有模糊推理能力，是进行知识表示和推理的有力工具，尤其适合用于描述和处理模糊知识工程中的并行问题，经常被用于进行故障诊断[10-11]。但由于利用模糊Petri网进行故障诊断时，常存在故障信息表达不够全面的问题。为了解决这个问题，直觉模糊Petri网应运而生。

直觉模糊Petri网是传统模糊Petri网的扩展，能够提供知识表示过程中更加丰富的信息，因此更适用于进行故障诊断。根据IFPN的定义和特点，本文所给出的直觉模糊Petri网对文献[3-4]中的直觉模糊Petri网进行了改进，可用一个七元组来表示。

定义4（直觉模糊Petri网）直觉模糊Petri网可以表示为IFPN=(P,T,Th,W,Δ,O,M)，其中：

（1）P={p1,p2,…,pn}是IFPN中库所的集合，表示利用IFPN进行故障诊断时用到的证据和结论库所的有限集合，n为库所的个数。

（2）T={t1,t2,…,tm}是对应于故障诊断推理中变迁的有限集合，每个变迁对应着一个直觉模糊产生式规则，m为变迁的个数。

（3）Th={τ1,τ2,…,τn}T为变迁的阈值集合，其中τj为直觉模糊数，可表示为τj=(αj,βj)(j=1,2,…,m)，(0<αj+βj≤1)，αj>0为变迁tj可信度的阈值，βj≥0表示变迁tj非可信度的阈值。

（4）W=WI(p,t)⋃WO(t,p)是有限输入输出权矩阵，若p是变迁t的输入库所，则W=WI(p,t)={wi1,wi2,…,win}为输入库所p到变迁t的权重向量，wij为输入库所pi到变迁ti上的输入权重，若变迁t有多个输入库所p1,p2,…,pn，则wi1+wi2+…+win=1。若p是变迁t的输出库所，则W=WO(t,p)={wo1,wo2,…,won}为变迁t到输出库所p上的规则可信度向量。这里μij为变迁ti到输出库所pj上的输出可信度，为直觉模糊数(μwO,γwO)。μwO为变迁t可信度的隶属度，γwO

为变迁t可信度的非隶属度。

（5）Δ={wij}为加权输入矩阵 (i=1,2,…,n;j= 1,2,…,m)，是库所到变迁的连接情况和每个连接弧的权系数。其中wij∈[0,1]且若库所pi是变迁tj的输入库所，则wij为pi到tj输入弧上的权系数。若库所pi不是变迁tj的输入库所，则wij等于0。

（6）O={aij}为输出矩阵(i=1,2,…,n;j=1,2,…,m)，反映了变迁到库所的连接情况及每个输出连接的可信度。若库所pj是变迁ti的输出库所，则aij等于变迁ti的可信度cj，其中cj为直觉模糊数，可表示为为变迁tj可信度的隶属度为变迁tj可信度的非隶属度。若库所pj不是变迁ti的输出库所，则aij等于0。

（7）M={M(pi)}(i=1,2,…,n)是库所集合上的标识向量，表示库所的可信度，可记作M=[M(p1),M(p2),…,M(pn)]T，其中M(pi)为直觉模糊数(μi,γi)。μi为库所pi可信度的隶属度，γi为库所pi可信度的非隶属度。关于直觉模糊产生式规则的3种类型表述以及基于直觉模糊Petri网的知识表示方法请参考文献[12-13]。

3.2 几个矩阵运算符

本文将给出可用于故障诊断的直觉模糊推理算法。该算法可将直觉模糊诊断推理的过程转化为矩阵运算的过程。在给出该诊断推理算法之前定义如下几个矩阵运算关系[7-9]。

定义5（矩阵运算关系）

（1）加法算子⊕:A⊕B=C⇔max(aij,bij)=cij，其中A、B、C均为n×m维直觉模糊矩阵；

由于矩阵A、B和C的元素均为直觉模糊数，矩阵需根据直觉模糊逻辑进行运算。

4 直觉模糊Petri网故障诊断推理算法

正向推理与反向推理是两种比较常用的推理方法，正向推理的优点是具有并行推理能力，并能够在推理结束后得到全部的值，其主要不足是推理具有盲目性。反向推理的优点是算法较简单，准确性较高，并且可以较大程度地避免冗余计算，主要不足是在选择初始目标时具有盲目性。根据这些情况，本文将正向推理与反向推理结合在一起，构成正反向混合推理。先根据目标征兆利用反向推理推理出有可能会产生的故障，再利用正向推理验证故障[14-16]。

4.1 IFPN故障诊断反向推理算法

该算法分为两个阶段：第一阶段包括步骤1到步骤5，这一阶段是获取FPN模型的目标库所的过程。第二阶段包括步骤6到步骤8[17-18]，这一阶段是不断调整库所的真实度，以确定引发目标库所所表示的事实的原因。

步骤1建立模糊Petri网模型，并根据目标库所给出初始标识M0。

步骤2写出输入矩阵I，输出矩阵O，并计算VI、VO和V，其中V根据以下公式计算：

这里，有：

（1）∀vi∈V，若vi=1，则相应的库所pi为中间库所

（2）∀vi∈V，若vi=0，则相应的库所pi为初始库所或是终止库所

其中V、VI和VO为n维向量；aij(i=1,2,…,m;j=1,2,…,n)为矩阵I的元素；bij(i=1,2,…,m;j= 1,2,…,n)为矩阵O的元素；| · |表示元素的模糊值。

步骤3对第k步迭代，变迁和标识值向量可根据以下公式计算：

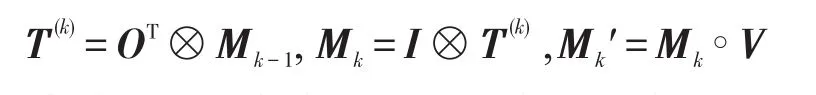
步骤4人工智能转换可根据以下情况进行：

问：Mk′中的哪个非零元素对应的命题可以充分转换？

答：pi可以，令向量Mk′中的第i个元素为0，即若向量Mkp不是零向量，则意味着Mk′中有中间库所，不能被充分转化，于是k=k+1，返回步骤3，否则转到步骤5。

步骤5

步骤6构造关联矩阵Ig和Og，在I和O中，删除与M中的零元素相关的库所对应的行。类似的，删除与T中零元素相关的库所对应的列，从而得到新的关联矩阵Ig和Og。

步骤7构造FPN模型的目标库所集。通过Ig和Og，FPN模型的目标库所集可根据初始FPN模型构造出来。由于一部分库所和变迁以及相应的连接弧已经被删除，初始FPN模型可能被分成几个FPN子模型，FPN子模型数量应小于等于目标库所的数量。

步骤8通过构建FPN模型，可计算出激发变迁的初始库所真实度，找到引发目标库所所表示的事实的原因。

算法分析：该算法的步骤3中Mk′的主要目的是为了减少后向推理查询或检查的次数，步骤4的主要目的是对结果库所的真实度已知的变迁的多个前件进行推理。

4.2 IFPN故障诊断正向推理算法

步骤1输入：加权输入向量ΔT={wij}，表示输入库所到变迁的权重向量。wij等于pi到tj输入弧上的权系数。输出矩阵On×m={μij}，表示变迁到输出库所的规则可信度矩阵。μij为变迁ti到输出库所pj上的输出可信度。

库所初始标识向量为：

定义在变迁集合T上的阈值向量为：

初始化各输入矩阵，令k=0,初始化向量值Mk=M0，其中Mk为第k次迭代的标识值。

步骤2计算各变迁输入库所可信度的直觉模糊值E0=ΔT·M0，其中Δ为输入的权重向量。

步骤3令G=E0⊙Th，将步骤2中计算出的直觉模糊值与阈值进行比较，判断各变迁能否激发，可知G应是(0,1)或(1,0)的m维直觉模糊列向量。

步骤4令H=E0⊗G，计算能成功激发的变迁的前件模糊值，其中H是m维直觉模糊向量。

步骤5激发满足激发条件的故障变迁并计算激发后输出库所的新模糊值M1=Γ∙H。

步骤6将新模糊值与原模糊值进行比较M1=M0⊕M1。

步骤7若M1≠M0，则令k=k+1，返回步骤1，若M1=M0，则推理结束，输出结果为M1。

5 诊断实例

现以汽车发动机故障为例来进行诊断建模分析。根据以下发动机故障图，建立发动机的故障诊断模型。

（1）库所集

（2）命题集

（3）规则集

由反向推理算法可知：

初始标识M0=(0 0 1 0 0 0 0 0 0 0 1 0 0 0)T，输入和输出矩阵分别为：

进行第一次迭代，k=1：

令p9为0，得到：

由于M1q不为零向量，则k=2：

由于M2q=M2′是零向量，则：

现根据以上算法计算简化后的推理结果，由正向推理算法可知：

首先令输入权矩阵为W。

初始标识为:

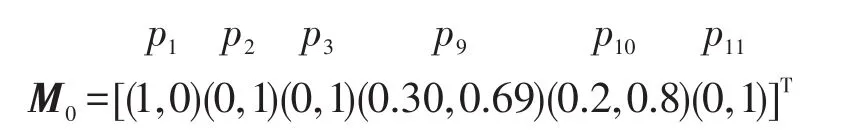
阈值向量为:

计算步骤：

（1）k=0,令Mk=M0（k为迭代次数）。

（2）δ=WT·M0=

M3=M2,与p11相比，p3发生故障的可能性最大，引起故障的最大原因为p1。

算例分析：本文给出的直觉模糊双向推理算法考虑了变迁阈值、输入权值以及规则可信度等多种约束条件，并定义了状态转移函数检测变迁状态的变化情况。这样就可以将已经激发而其状态转移函数值没有增大的变迁剔除，以避免变迁的重复激发以及可能出现的循环问题，使得推理过程更加高效。

另外直觉模糊双向推理算法在推理过程中只考虑与目标库所相关的库所及变迁，避免无关的路径推理，因此能够避免冗余，简化不必要的推理过程。算法在推理过程中是并行的，因此直觉模糊推理的步数只与直觉模糊推理的最大深度有关。上面例子中的最大直觉模糊推理深度为2，因此只需要两步即能得到最终的推理结果。该算法若能将现场实测数据与专家经验数据相结合，则可以使诊断结果更加符合实际情况。

6 结论

本文提出了基于直觉模糊Petri网的双向模糊故障推理算法。本文算法充分利用了模糊Petri网的并行处理能力，利用直觉模糊反向推理算法对模型进行约减，再利用正向直觉模糊推理算法对模型进行计算，不仅将故障信息化繁为简，降低了推理过程的时间复杂度，还能够达到使故障诊断的确定性程度得到进一步提高的目的。算法还提供了引起故障的原因隶属度、非隶属度等更丰富的故障信息，具有一定的实际意义和应用价值。

[1]Wang Huiying,Yue Xiaobo,Zhou Kaiqing.A bi-directional parallel reasoning algorithm based on fuzzy petri nets[J]. Computer Engineering,2014,40(3):208-212.

[2]Huang Min,Lin Xiao,Hou Zhiwen.Modeling method of fuzzy fault Petri nets and its application[J].Journal of Central South University:Science and Technology,2012,44 (1):208-215.

[3]Yu Ping,Cao Jiping,Song Jianshe,et al.Improved fuzzy Petri net algorithm and its application in fault diagnosis[J]. Ordnance IndustryAutomation,2011,30(6):20-22.

[4]Wu Shuang,He Zhengyou,Qian Chenghao,et al.Application of fuzzy Petri net in fault diagnosis of traction power supply system for high-speed railway[J].Power System Technology,2011,35(9):79-85.

[5]Szmidt E,Kacprzyk J.Correlation of intuitionistic fuzzy sets[C]//LNCS 6178:Proceedings of the 13th International Conference on Information Processing and Management of Uncertainty,Dortmund,Germany,Jun 28-Jul 2,2010.Berlin,Heidelberg:Springer,2010:169-177.

[6]Wei Guiwu.Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making[J].Expert Systems withApplications,2011,38(9):11671-11677.

[7]Park J H,Hwang J H,Park W J,et al.Similarity measure on intuitionistic fuzzy sets[J].Journal of Central South University,2013,20(8):2233-2238.

[8]Xu Zeshui,Cai Xiaoqiang.Recent advances in intuitionistic fuzzy information aggregation[J].Fuzzy Optimization and Decision Making,2010,9(4):359-381.

[9]Yager R R.Level sets and the representation theorem for intuitionistic fuzzy sets[J].Soft Computing,2010,14(1):1-7.

[10]Hu Hesuan,Li Zhiwu,Al-Ahmari A.Reversed fuzzy Petri nets and their application for fault diagnosis[J].Computers &Industrial Engineering,2011,60(4):505-510.

[11]Liu Huchen,Lin Qinglian,Ren Minglun.Fault diagnosis and cause analysis using fuzzy evidential reasoning approach and dynamic adaptive fuzzy Petri nets[J].Computersand Industrial Engineering,2013,66(4):899-908．

[12]Sun Xiaoling,Wang Ning.Fault diagnosis based on intuitionistic fuzzy Petri nets[J].Computer Engineering and Science,2014,36(9):1736-1741.

[13]Sun Xiaoling,Wang Ning.Weighted intuitionistic fuzzy reasoning based on intuitionistic fuzzy Petri nets[J].Computer Engineering andApplications,2013,49(4):50-53.

[14]Zhou Chuangming,Shen Xiaoyong,Lei Yingjie.Research of FOE intention recognition method based on intuitionistic fuzzy Petri net[J].Journal of Computer Applications,2009, 29(9):2464-2467.

[15]Xiang Yongsheng,Liu Wu,Yue Xiaobo,et al.Research on the auto fault diagnosis simulation based on fuzzy petri nets [J].Computer Engineering and Science,2009,31(3):86-89.

[16]Lei Yingjie,Wang Baoshu,Lu Yanli.Approximate reasoning method based on intuitionistic fuzzy logic[J].Control and Decision,2006,21(3):305-310.

[17]Sun Xiaoling,Wang Ning,Liang Yan.Fuzzy reasoning by using marked fuzzy Petri nets[J].Computer Engineering and Science,2012,34(3):152-157.

[18]Sun Xiaoling,Wang Ning.Method of knowledge representation based on marked fuzzy Petri net[J].Computer Engineering andApplications,2010,46(6):48-51.

附中文参考文献：

[1]王惠英,乐晓波,周恺卿.一种基于模糊Petri网的双向并行推理算法[J].计算机工程,2014,40(3):208-212.

[2]黄敏,林啸,侯志文.模糊故障Petri网建模方法及其应用[J].中南大学学报:自然科学版,2012,44(1):208-215.

[3]喻平,曹继平,宋建社,等.改进的模糊Petri网算法及其在故障诊断中的应用[J].兵工自动化,2011,30(6):20-22.

[4]吴双,何正友,钱澄浩,等.模糊Petri网在高速铁路牵引供电系统故障诊断中的应用[J].电网技术,2011,35(9):79-85.

[12]孙晓玲,王宁.基于直觉模糊Petri网的故障诊断[J].计算机工程与科学,2014,36(9):1736-1741.

[13]孙晓玲,王宁.基于直觉模糊Petri网的加权直觉模糊推理[J].计算机工程与应用,2013,49(4):50-53.

[14]周创明,申晓勇,雷英杰.基于直觉模糊Petri网的敌意图识别方法研究[J].计算机应用,2009,29(9):2464-2467.

[15]向永生,刘武,乐晓波,等.基于模糊Petri网的汽车故障诊断仿真研究[J].计算机工程与科学,2009,31(3):86-89.

[16]雷英杰,王宝树,路艳丽.基于直觉模糊逻辑的近似推理方法[J].控制与决策,2006,21(3):305-310.

[17]孙晓玲,王宁,梁艳.应用带标识的模糊Petri网的模糊推理[J].计算机工程与科学,2012,34(3):152-157.

[18]孙晓玲,王宁.应用带标识的模糊Petri网的知识表示方法[J].计算机工程与应用,2010,46(6):48-51.

孙晓玲（1977—），女，安徽合肥人，2006年于河北大学获得硕士学位，现为合肥师范学院副教授，主要研究领域为不确定性模糊推理，模糊Petri网等。现主持安徽省高校省级自然科学重点项目。

Bidirectional Fuzzy Fault ReasoningAlgorithm of Intuitionistic Fuzzy Petri Net*

SUN Xiaoling+
School of Mathematics and Statistics,Hefei Normal University,Hefei 230601,China
+Corresponding author:E-mail:sxl_hftc@126.com

According to the complicated uncertain relation between fault phenomenon and fault reason in fault diagnosis,using the advantage of intuitionistic fuzzy sets in expressing uncertainty information and the ability of graphics processing of Petri net,this paper presents a bidirectional fuzzy fault diagnosis inference algorithm based on intuitionistic fuzzy Petri nets.The reverse intuitionistic fuzzy reasoning algorithm is firstly applied to the model reduction in order to find the cause of the fault.The positive intuitionistic fuzzy reasoning algorithm is used to calculate the model and then output the results.The algorithm can not only simplify the fault information and reduce the time complexity of the inference process,but also can improve the fault diagnosis degree of certainty.Automobile engine diagnosis shows that the bidirectional intuitionistic fuzzy reasoning algorithm is feasible and effective.

intuitionistic fuzzy Petri nets;intuitionistic fuzzy reasoning;fault diagnosis;bidirectional fuzzy fault reasoning

ing was born in 1977.She

the M.S.degree from Hebei University in 2006.Now she is an associate professor at Hefei Normal University.Her research interests include uncertainty fuzzy reasoning and fuzzy Petri nets,etc.

A

TP182

*The Key Natural Science Research Project of Anhui Province under Grant No.KJ2016A580(安徽省高等学校省级自然科学研究重点项目).

Received 2016-03,Accepted 2016-06.

CNKI网络优先出版:2016-06-02,http://www.cnki.net/kcms/detail/11.5602.TP.20160602.1144.006.html