测试代价敏感的决策粗糙集正域约简*

刘 偲，秦亮曦

广西大学 计算机与电子信息学院，南宁 530004

测试代价敏感的决策粗糙集正域约简*

刘 偲+，秦亮曦

广西大学 计算机与电子信息学院，南宁 530004

LIU Cai,QIN Liangxi.Test-cost sensitive reduction on positive region of decision theoretic rough sets.Journal of Frontiers of Computer Science and Technology,2017,11(6)：1014-1020.

对测试代价敏感的决策粗糙集（decision theoretic rough sets，DTRS）正域约简问题进行了研究。在传统正域约简的基础上将测试代价考虑进来，希望找到测试代价总和最小的正域约简。采用模拟退火算法结合传统决策粗糙集正域约简算法来搜索测试代价总和最小的正域约简结果。提出了一种测试代价敏感的决策粗糙集正域约简算法TCSPR（test-cost sensitive positive region-based reduction algorithm for DTRS），并分析了该算法的时间复杂度。实验结果验证了TCSPR算法的有效性，该算法能在多项式时间内找到一个属性更少、测试代价更小的正域约简，找到的解一般为优化目标的最优解或次优解，即测试代价总和最小的正域约简,并且该算法在部分数据集上的分类能力几乎不减。

决策粗糙集（DTRS）；代价敏感；属性约简

1 引言

经典粗糙集模型[1]是由Pawlak在1982年提出的一种处理模糊性和不确定性的软计算工具[2]。因为经典粗糙集是基于严格的集合代数包含关系，所以在容错能力方面具有较大的局限性。Yao将经典粗糙集的严格代数包含关系改为概率包含关系，这样就使得决策类的负域不恒为空，并赋予3个决策域新的语义，重新定义了一个新的模型，即决策粗糙集模型[3]。

属性约简是粗糙集研究的核心问题之一，其目的是将冗余的属性去掉，从而发现数据的本质信息。众所周知，经典粗糙集的正域是具有单调性的，Pawlak基于这一特性给出了正域约简的方法[4]，而决策粗糙集并不具备这个特性，Yao等人为此提出了新的正域约简方法[5]。

一般而言，样本的分类结果与测试属性集紧密相关。在一定范围内，测试的相关属性越多，样本的分类精度越高，错误分类结果越少，误分类代价越小[6]。因此，包含更多属性的测试属性集通常具有较小的误分类代价。但在实际问题中，获取样本的属性值本身具有一定的代价，即测试代价[7]。例如，在医疗诊断中，取得病人的视力数据、心电图数据、尿检数据、血常规数据等都需要不同的测试代价[8]。测试属性集越多，虽然分类精度越高即误分类代价越低，但是同样的测试代价也越高。因此，需要将测试代价考虑在内，使包括误分类代价和测试代价的总代价降到最低，才能适应实际问题的需求。在决策粗糙集属性约简方面，Yao提出了正域约简方法，黄国顺提出了一种保正域的属性约简方法[9]，张智磊等人给出了一种基于回溯搜索算法的属性约简方法[10]，贾修一等人提出了一种决策风险最小化属性约简[11]，李华雄等人在文献[11]的基础上给出了代价敏感的决策风险最小化属性约简方法[6]。

本文将测试代价纳入正域约简的考虑范围，在正域约简的基础上用模拟退火方法找到测试代价总和最小的正域约简结果。通过找到测试代价总和最小的正域约简，可以在实际应用中，找到一个分类能力和属性全集相近但测试代价大大降低的属性约简。

2 相关理论介绍

2.1 决策粗糙集正域约简

在经典粗糙集正域约简中，因为经典粗糙集具有正域单调性，所以Pawlak正域约简要求属性子集的正域保持不变。但是决策粗糙集模型中，正域不具备单调性，即正域不会随着属性的增加而扩大。针对决策粗糙集的这种情况，Yao等人在文献[5]中给出了新的属性约简定义。

定义1[5]设S={U,C∪D,f,V}为一个决策表，若属性子集B⊆C满足以下两个条件：

（2）属性独立性，对任意属性a∈B,均有|POSαB-{a}(D)|<则称属性子集B为属性全集C的一个决策粗糙集α-正域约简。

如果属性子集同时满足上述两个性质，则属于一个正域约简，正域约简可能不止一个。

2.2 决策粗糙集正域约简算法

目前已知求粗糙集的最小属性约简是一个NP难问题，因此大多数求约简的方法都采用启发式方法，通过定义启发式函数为搜索方向提供指导，以搜索出部分约简。在决策粗糙集中求约简的方法可以采用启发式策略，根据定义1可知，在求决策粗糙集α-正域约简时，属性子集应具有尽可能大的正域，因此可以将启发式函数选为属性的α-正域重要度[12]。

定义2[12]设S={U,C∪D,f,V}为一个决策表，α∈[0,1]为条件概率阈值，a∈C为单个属性，则属性a的α-正域全局重要度为：

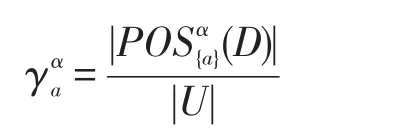
文献[12]给出了决策粗糙集α-正域约简算法。

算法1[12]PRDTRS（positive region-based heuristic reduction algorithm for DTRS）

输入：一个决策表S={U,C∪D,f,V}，概率包含度阈值α∈[0,1]。

输出：该决策表的α-正域约简。

步骤1令初始α-正域约简属性集B=∅。

步骤2计算C中每个属性的α-正域全局重要度γ

步骤3将属性按照全局重要度由大到小排列，令为P。

步骤4在时重复如下循环：令a为P中第一个属性（最高重要度）；将α并入α-正域约简属性集，B=B∪{a}；将α从P中删除，P=P-{a}。

步骤5在B不满足独立性条件时重复如下循环：对所有c∈B,若则B=B-{c}。

步骤6输出该决策表的一个α-正域约简。

3 测试代价敏感与属性约简

3.1 测试代价敏感

将数据集表示为如下四元组形式的决策信息表：

S={U,C∪D,f,V}

定义属性子集B⊆C上的等价关系RB和样本x⊆U在属性集B下的等价类分别为[6]：

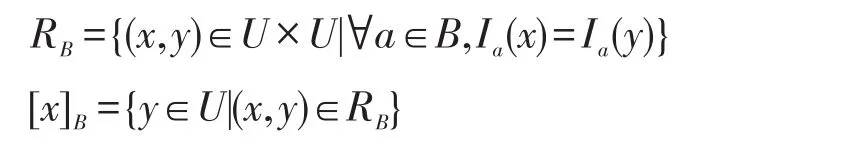
在考虑样本x在属性子集B上的测试代价时，假设各个样本在同一属性上的测试代价是相等的，因此，x在属性子集B上的测试代价为属性子集B中所有属性测试代价的和，测试代价设为一个非负实数。可以得到一个计算测试代价函数[6]：

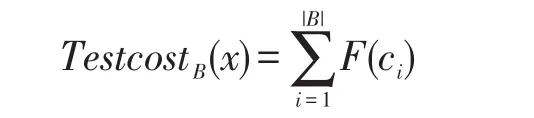
其中，F(ci)为B中单个属性的测试代价。

3.2 属性约简

在传统决策粗糙集正域约简中，不考虑测试代价，只考虑正域的变化。本文将在保证正域不减的同时，寻找属性子集中测试代价总和最小的属性集合，提出一种测试代价敏感的决策粗糙集正域约简算法TCSPR（test-cost sensitive positive region-based reduction algorithm for DTRS）。该算法的目标是在满足正域不变约束的情况下求总测试代价最小的属性子集B，即其中k为样本个数，x为样本对象，TestcostB(x)为求x对象在属性集合B下的测试代价，算法思想如下：

首先，通过算法1的前4步找到一个属性子集，该属性子集的正域不小于属性全集的正域，用该属性子集作为初始集合。然后，结合模拟退火的方法[13-14]，在温度的每个平衡点用随机变换产生属性子集，并在当前温度下判断是否保留此变换。最后保留下来的即为测试代价总和最小的正域约简。

算法2TCSPR

输入：一个决策表S={U,C∪D,f,V}，由算法1前4步得到的属性子集BOringe。

输出：测试代价敏感的正域约简。

步骤1令初始正域约简属性集B=BOringe，令P=C-BOringe，计算初始化tmin,t。

步骤2通过随机删除、替换、添加属性的方式，由属性集B产生新的B*。

步骤5如果或者exp(-Δf/t)>Random，并且则令B=B*。

步骤6判断当t>tmin并且结果不收敛时，回到步骤2，并让t衰减一个Δt。

步骤7输出B即为测试代价总和最小的正域约简。

算法1中，添加属性循环复杂度为O(C×N2)，删除属性循环复杂度为O(C×N)，因此算法1的时间复杂度为O(C×N2+C×N)，也就是O(C×N2)，其中C为属性个数，N为样本个数。在算法2中，目标函数的时间复杂度为O(C×N2)，算法2是基于模拟退火算法的，模拟退火的时间复杂度为O(|Nm|×ln|S|)，其中|S|为状态空间中的状态数，|Nm|为最大的相邻状态数。该问题的|N|和|S|为问题输入大小的多项式函数，即该算法可在多项式时间内为这些问题求得近似最优解或者最优解[13]。

算法2有两个结束条件，一个是温度下降到阈值，一个是结果收敛，如果出现解在连续M个马尔可夫链无任何改变的情况可以判断为结果收敛。结果如果一直不收敛，初始温度t也一定会下降到阈值tmin而结束该算法，且模拟退火算法已经从理论上被证明是可收敛的，只是收敛较慢[13]。因此在运行时间上还是算法1具有明显优势，但是在测试代价总和方面，算法2具有绝对优势，下面通过实验具体说明。

4 实验结果及分析

这一部分主要验证基于模拟退火算法的测试代价敏感决策粗糙集正域约简方法的有效性，并和传统决策粗糙集正域约简算法进行比较。

模拟退火算法是一种随机算法，每次运行的状态可能不一致，因此对每个数据集都运行10次取平均值作为运行结果。

本文实验的机器为Intel®Xeon®的3.50 GHz CPU，8 GB内存，64位Windows8操作系统，算法在Matlab平台上实现。实验数据取自UCI数据库中的3个数据集Spambase、WDBC（breast cancer Wisconsin（diagnostic）肺癌诊断结果）和WPBC（breast cancer Wisconsin（prognostic）患者是否复发）。数据集中有少量缺失的数据，使用该属性在其他所有对象中的最频值来补齐缺失的属性值。WDBC、WPBC有数据ID列，将该列删除，然后使用WEKA（Waikato environment for knowledge analysis）归一化、离散化。预处理之后的实验数据基本信息如表1所示。

Table 1 Basic information of experimental data表1 实验数据基本信息

在实验中，假定[15]误分类代价满足λPP≤λBP≤λNP,λNN≤λBN≤λPN,λNN=λPP=0，为使实验具有可重复性，3组数据的误差代价矩阵如表2所示[6]。

Table 2 Misclassification cost matrix表2 误分类代价矩阵

数据集中没有给出各属性的测试代价，因实验需要，本文假定各测试代价服从正态分布N(μ,σ)，并设Spambase的属性测试代价服从N(0.2,0.1)，WDBC和WPBC的属性测试代价服从N(0.02,0.01)，使用正态随机函数随机生成各属性的测试代价。

本文实验随机选用数据中的100个样本作为训练样本，为使实验具有可重复性，固定选取前100个样本作为训练样本，剩下的对象作为测试样本[6]。分别使用算法1和算法2计算局部最优属性集B*，然后用风险最小化分类方法对测试样本进行分类，得到分类正确率。

表3为3组属性约简实验结果（比较约简属性集平均个数）。

由表3可以看出，算法2约简后得到的最优属性集个数更少，特别是在WPBC数据集上，算法2在算法1的基础上约简了77%的属性个数，但是正域对象个数和算法1得到的正域对象个数相差无几，且算法2约简后的平均正域对象个数都大于等于全属性集的正域对象个数。证明算法2能在保证约简后正域对象个数不减的情况下得到属性个数更少的正域约简最优属性集，即具有更强的属性约简能力。

Table 3 Comparison of experimental results表3 实验结果比较

表4比较了3组实验的平均测试代价总和。从表4可以很明显地看出，算法2能大大降低测试代价总和。在3个数据集上，算法2在算法1的基础上测试代价约简率都超过了50%，特别在WPBC数据集上，算法2能在算法1的基础上再降低96.2%的总测试代价。证明算法2确实可以实现找到最小测试代价总和的正域约简。

Table 4 Average total test cost表4 平均总测试代价

表5展示了3组实验约简得到的最优属性集，对测试样本集进行风险最小化的决策粗糙集决策分类的平均正确率。

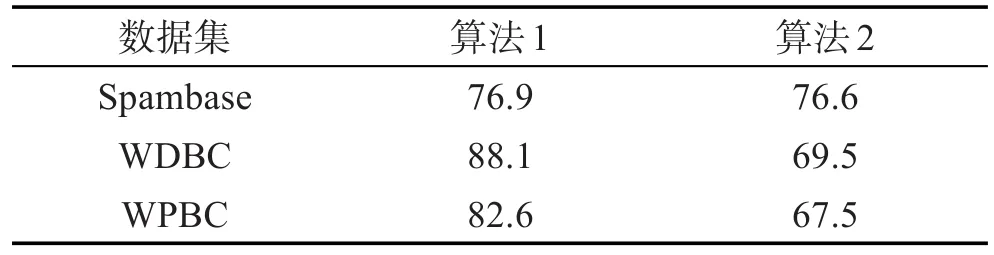
Table 5 Average correct rate of classification表5 分类平均正确率 %

由表5可以看出，算法1在3个数据集上的分类正确率都比较高，而算法2只有在数据集Spambase上正确率和算法1相近，在另外两个数据集上的正确率略低于算法1。由实验可以看出，在数据集Spambase上，相对算法1的测试代价约简率只为57.9%，属性约简率只有32%；在WDBC和WPBC平均正确率较低的数据集上测试代价约简率高达96.1%和 96.2%，属性约简率高达67%和77%。说明单单追求测试代价的最小化将导致正确率的下降。

由此可以看出，算法2在某些数据集上的正确率较低，因此算法2不适用于要求分类正确率较高的场合。

表6展示了两个算法的平均运行时间。运行时间是通过使用Matlab自带的记录运行时间方式统计得到。通过实验可以看出，算法1的运行时间比算法2还要低许多，在运行时间方面算法1比较有优势。当然，如果调小判断结果收敛的参数M，则收敛速度会变快，但是测试总代价约简率将会下降，反之则变慢，但是更接近全局最优解。

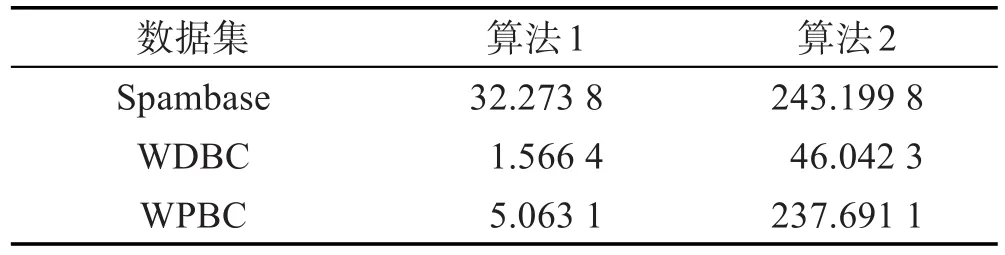
Table 6 Average running time表6 平均运行时间 s

图1~图4分别展示了算法1和算法2在约简属性集平均个数、平均总测试代价（因为数量级不一致，将3组都化为同一数量级显示）、分类平均正确率和平均运行时间的比较。

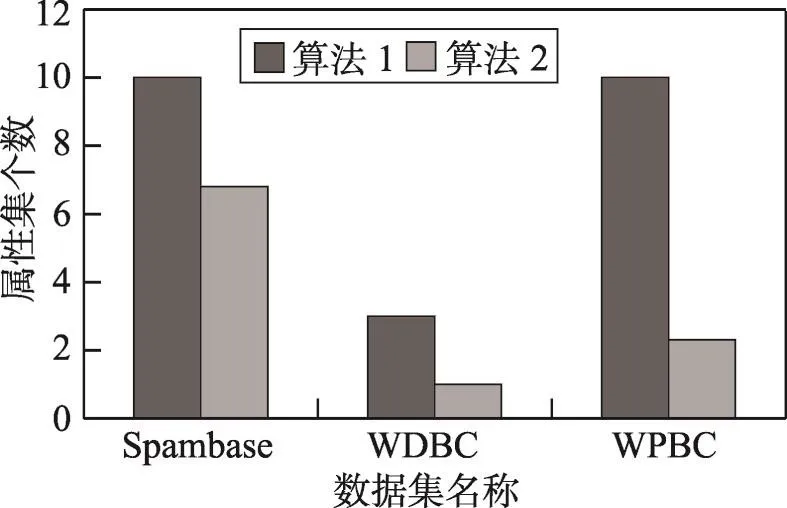
Fig.1 Average number of reduction attribute set图1 约简属性集平均个数

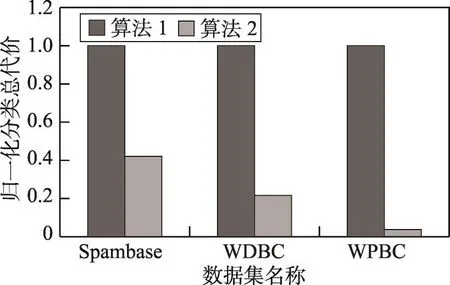
Fig.2 Average total test cost图2 平均总测试代价

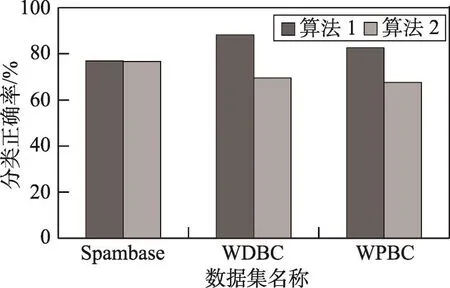
Fig.3 Average correct rate of classification图3 分类平均正确率

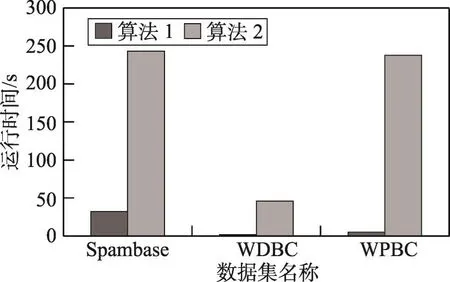
Fig.4 Average running time图4 平均运行时间

从图1~图3中可以更清楚地看出，算法2相比较算法1，能实现更高的属性约简率，能大大降低测试代价总和，而且分类正确率相差不大。这在实际应用中，如果各属性的测试代价较高，而且决策者并不需要较高的分类正确率时，算法2可以帮助决策者节省大量花费在获取数据上的成本。然而从图4上也能看出，在运行时间方面，算法2还有很大的改进空间。本文在正域约简的基础上，用模拟退火算法来搜索具有最小测试代价总和的正域约简，虽然已经达到了大大减少测试代价总和的正域约简，属性约简率也有很大的提高，但是在正确率方面还有待提高。这也证明了全力搜索具有最小测试代价总和的正域约简有一定的局限性，并不是测试代价越低的正域约简越好。应当在搜索具有最小测试代价总和的正域约简的同时，考虑误差代价，提高分类正确率。下一步准备在考虑测试代价敏感的同时考虑误差代价，将误差代价也引入正域约简。

5 结束语

本文针对测试代价敏感和决策粗糙集的正域约简进行了研究，在传统正域约简的基础上将测试代价考虑进来，提出了一种测试代价敏感的正域约简算法TCSPR，通过采用模拟退火方法结合传统正域约简算法来搜索测试代价总和最小的正域约简结果。通过实验分析，验证了本文提出的TCSPR算法的有效性，分析了TCSPR算法的时间复杂度为O(|Nm|×ln|S|)，即能在多项式时间内找到属性个数更少的测试代价更小的正域约简，找到的解一般为优化目标的最优解或次优解。并且TCSPR算法在部分数据集上的分类能力几乎不减。但是因为算法1的时间复杂度较低，所以TCSPR算法在运行时间方面要明显弱于算法1，这也是下一步需要改进的地方。而且如果一味追求测试代价最小化可能会引起正确率的下降，因为属性个数越少测试代价也会越小，但是误分类代价将上升，导致正确率下降。下一步也将进一步研究如何在降低测试代价的同时，考虑引入误差代价保持分类的正确率。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(5):341-356.

[2]Wang Guoying,Yao Yiyu,Yu Hong.A survey on rough set theory and applications[J].Chinese Journal of Computers, 2009,32(7):1229-1246.

[3]Yao Yiyu.Decision-theoretic rough set models[C]//LNCS 4481:Proceedings of the 2nd International Conference on Rough Sets and Knowledge Technology,Toronto,Canada,May 14-16,2007.Berlin,Heidelberg:Springer,2007:1-12.

[4]Pawlak Z.Rough sets theoretical aspects of reasoning about data[M].Boston,USA:KluwerAcademic Publishers,1991.

[5]Yao Yiyu,ZhaoYan.Attribute reduction in decision-theoretic rough set models[J].Information Sciences,2008,178(17): 3356-3373.

[6]Li Huaxiong,Zhou Xianzhong,Huang Bing,et al.Decisiontheoretic rough set and cost-sensitive classification[J].Journal of Frontiers of Computer Science and Technology,2013, 7(2):126-135.

[7]Min Fan,He Huaping,Qian Yuhua,et al.Test-cost-sensitive attribute reduction[J].Information Sciences,2011,181(22): 4928-4942.

[8]Liu Jiabin,Min Fan.A survey on cost-sensitive rough set research[J].Journal of Zhangzhou Normal University:Natural Science,2011,24(4):17-22.

[9]Huang Guoshun.Positive region preservation reducts in decision-theoretic rough set models[J].Computer Engineering andApplications,2016,52(2):165-169.

[10]Zhang Zhilei,Liu Sanyang.Decision-theoretic rough set attribute reduction based on backtracking search algorithm [J].Computer Engineering and Applications,2016,52(10): 71-74.

[11]Jia Xiuyi,Shang Lin,Chen Jiajun.Attribute reduction based on minimum decision cost[J].Journal of Frontiers of Computer Science and Technology,2011,5(2):155-160.

[12]Li Huaxiong,Zhou Xianzhong,Zhao Jiabao,et al.Nonmonotonic attribute reduction in decision-theoretic rough sets[J].Fundamenta Informaticae,2013,126(4):415-432.

[13]Yao Xin,Chen Guoliang.Simulated annealing algorithm and its applications[J].Journal of Computer Research and Development,1990,27(7):1-6.

[14]Jia Xiuyi,Shang Lin.A simulated annealing algorithm for learning thresholds in three-way decision-theoretic rough set model[J].Journal of Chinese Computer Systems,2013,34 (11):2603-2606.

[15]Li Huaxiong,Liu Dun,Zhou Xianzhong.Rewiew on decisiontheoretic rough set model[J].Journal of Chongqing University of Posts and Telecommunications:Natural Science Edition, 2010,22(5):624-630.

附中文参考文献：

[2]王国胤,姚一豫,于洪.粗糙集理论与应用研究综述[J].计算机学报,2009,32(7):1229-1246.

[6]李华雄,周献中,黄兵,等.决策粗糙集与代价敏感分类[J].计算机科学与探索,2013,7(2):126-135.

[8]刘家彬,闵帆.代价敏感粗糙集研究综述[J].漳州师范学院学报:自然科学版,2011,24(4):17-22.

[9]黄国顺.保正域的决策粗糙集属性约简[J].计算机工程与应用,2016,52(2):165-169.

[10]张智磊,刘三阳.基于回溯搜索算法的决策粗糙集属性约简[J].计算机工程与应用,2016,52(10):71-74.

[11]贾修一,商琳,陈家骏.决策风险最小化属性约简[J].计算机科学与探索,2011,5(2):155-160.

[13]姚新,陈国良.模拟退火算法及其应用[J].计算机研究与发展,1990,27(7):1-6.

[14]贾修一,商琳.一种求三支决策阈值的模拟退火算法[J].小型微型计算机系统,2013,34(11):2603-2606.

[15]李华雄,刘盾,周献中.决策粗糙集模型研究综述[J].重庆邮电大学学报:自然科学版,2010,22(5):624-630.

LIU Cai was born in 1991.He is an M.S.candidate at Guangxi University.His research interests include decision theoretic rough sets,data mining and machine learning,etc.

刘偲（1991—），男，湖南岳阳人，广西大学计算机与电子信息学院硕士研究生，主要研究领域为决策粗糙集，数据挖掘，机器学习等。

秦亮曦（1963—），男，广西灵川人，2005年于中国科学院大学计算机软件与理论专业获得博士学位，现为广西大学教授，主要研究领域为数据挖掘，决策粗糙集等。

Test-Cost Sensitive Reduction on Positive Region of Decision Theoretic Rough Sets*

LIU Cai+,QIN Liangxi
School of Computer,Electronics and Information,Guangxi University,Nanning 530004,China
+Corresponding author:E-mail:liucaitc@163.com

This paper studies the test-cost sensitive reduction on the positive region of decision theoretic rough sets (DTRS).Based on the traditional positive region-based reduction,this paper takes test cost into account for the purpose of discovering the positive region-based reduction with the minimum total test cost,and adopts the simulated annealing algorithm combined with traditional positive region-based reduction of DTRS algorithm to search for the result of the positive region-based reduction with the minimum test cost.Furthermore,this paper proposes a testcost sensitive positive region-based reduction algorithm for DTRS(TCSPR),and analyzes the time complexity of the algorithm.The experimental results confirm the effectiveness of TCSPR that can find a positive region reduction with fewer attributes and less test cost in polynomial time,and whose solution is generally the optimum solution or second-best solution of the optimization objective,viz.the positive region-based reduction with the minimum total test cost,and whose classification ability is hardly reduced in part of the data sets.

decision theoretic rough sets(DTRS);cost sensitive;attribute reduction

xi was born in 1963.He

the Ph.D.degree in computer software and theory from University of Chinese Academy of Sciences in 2005.Now he is a professor at Guangxi University.His research interests include data mining and decision theoretic rough sets,etc.

A

TP181

*The National Natural Science Foundation of China under Grant No.61363027(国家自然科学基金).

Received 2016-03,Accepted 2016-08.

CNKI网络优先出版:2016-08-15,http://www.cnki.net/kcms/detail/11.5602.TP.20160815.1659.002.html