大规模集群上多维FFT算法的实现与优化研究*

李 琨，贾海鹏，曹 婷，张云泉

1.中国科学院 计算技术研究所 计算机体系结构国家重点实验室，北京 100190

2.中国科学院大学 计算机与控制学院，北京 100190

大规模集群上多维FFT算法的实现与优化研究*

李 琨1,2+，贾海鹏1，曹 婷1，张云泉1

1.中国科学院 计算技术研究所 计算机体系结构国家重点实验室，北京 100190

2.中国科学院大学 计算机与控制学院，北京 100190

LI Kun,JIA Haipeng,CAO Ting,et al.Implementation and optimization of multidimensional FFT algorithm on large-scale clusters.Journal of Frontiers of Computer Science and Technology,2017,11(6)：863-874.

快速傅里叶变换（fast Fourier transform，FFT）是用于计算离散傅里叶变换（discrete Fourier transform，DFT）或其逆运算的快速算法，在工程、科学和数学领域的应用非常广泛，例如信号分解、数字滤波、图像处理等。因此，在实际应用中对FFT算法进行细粒度优化是非常重要的。研究了FFT算法常用的分解策略以及FFT算法在大规模集群系统上的并行实现，并提出了相关的优化策略。在此基础上，对多种FFT算法在不同平台上进行了性能评估，并分析了各算法的实现、优缺点及其在大规模计算时的可扩展性。实验结果表明，相关研究有助于对现有的FFT算法进行进一步的优化，以及指导如何在大规模CPU+GPU的异构系统上根据不同需求选择实现性能更优的FFT算法。

集群；快速傅里叶变换（FFT）；消息传递接口（MPI）；性能优化

1 引言

快速傅里叶变换（fast Fourier transform，FFT），是用于计算序列的离散傅里叶变换（discrete Fourier transform，DFT）或其逆变换的一种高效算法。FFT被广泛应用于工程、科学和数学领域，如在国际大科学工程平方公里阵列射电望远镜（square kilometer array，SKA）[1]的数据处理中，FFT占总计算量的40%，且由于其每秒TB级的数据量及底层高性能计算机系统的规模和复杂度，对FFT算法的计算效能提出了更高的要求，需针对性地研究相应的方法。鉴于此，本文简要介绍了FFT的经典算法——库利图基算法，针对集群系统研究了并行FFT算法现存的瓶颈以及相应的优化策略，最后完整地将FFTW库（faster Fourier transform in the West）、PFFT库（parallel FFT library）与MPFFT库（massive parallel FFT library）3种算法在不同平台上进行了性能评估与分析。

本文的主要创新点如下：

（1）分析了PFFT和MPFFT算法的优化现状，指出目前大规模集群上FFT算法存在的两点可优化方向，一是数据在主存和设备内存间的不断通信，使得PCI-E总线带宽成为了性能瓶颈；二是在数据输出的同时可以进行细节上的处理，以更细致的划分方式避免最后数据的整体调整。

（2）在深入分析目前主流的几种FFT算法基础上，研究了一维分解、二维分解的优化策略，并提出了通信优化和输出优化两种改进方案。通信优化将数据在CPU和GPU间的传输进行了更细致的分解，将有效地提高整体的通信效率，减少全局转置所需的时间；输出优化在每一块数据进行FFT计算的同时确定好最优的内存分布位置，便于对计算后的数据进行排列，如此可使得FFT计算的同时进行数据的整理，减少额外进行转置的开销。

（3）在单节点平台和天河一号、天河二号超级计算机上通过对各种规模输入数据进行大量的测试和统计，详细地评估与分析了3种主流FFT算法的性能、可扩展性以及各算法的最佳适应环境，为FFT在大规模计算时的算法选择提供了参考。实验表明，在大多数情况下PFFT算法与MPFFT算法要优于FFTW算法，且当输入数据量较小时，MPFFT算法性能优势相对明显；输入数据量较大时，PFFT算法性能优势则相对明显。另外，这种性能优势会随着进程数量的增加而更为突出，当进程数量较小时，3种算法的性能优劣对比并不明显。

本文组织结构如下：第2章介绍了相关工作；第3章介绍了FFT的库利图基算法；第4章对FFTW、PFFT、MPFFT算法的分解策略和实现方法进行了分析，针对3种算法的性能瓶颈提出了两种优化策略；第5章在单节点和大规模集群上使用不同的输入规模对3种算法进行了性能评估和性能分析；第6章进行了总结讨论。

2 相关工作

目前常用的FFT库有FFTW[2]、PFFT[3]、MPFFT[4]、CUFFT[5]（CUDA fast Fourier transform library）、PKUFFT[6-7]（Peking University fast Fourier transform library）等。Frigo和Johnson开发的FFTW库可以计算一维或者多维实数据、复数据的离散傅里叶变换，其具备自适应性，并为各种领域内所需的FFT计算提供了基本的运行框架。PFFT算法是在FFTW库上的拓展，其加强了FFTW软件库的MPI（message passing interface）部分以适于多维的数据分解，即规模为Nd的d维FFT可以至多被Nd-1个MPI进程并行计算[8]。中国科学院李焱等人提出了FFT针对GPU平台的自适应性能优化框架和针对CPU和GPU异构集群的MPFFT软件包，融合了异构平台的硬件异同和FFT算法的特性，使得FFT在这些平台都能取得良好的加速效果[4]。CUFFT是NVIDIA SDK中提供的FFT库，它的API接口与FFTW比较相像，包括FFT plan的搜索阶段和执行阶段。另外陈一峯等人通过将数据各维度进行细粒度划分，利用GPU通信缓冲区与GPU Pinned Memory之间拷贝的机会对数据进行粒度上的调整来优化AlltoAll通信，使得PKUFFT取得了较高的性能[6]。

与以上工作不同，本文分析了各种库的并行分解策略以及各自的优势和不足，从通信、输出等多方面对FFTW、PFFT、MPFFT算法提出了可能的改进方案，并对3种算法在大规模集群上的性能进行了全面的评测和分析，所得结果可为3种算法今后的优化方向及在大规模计算时FFT算法的选择提供参考。

3 背景介绍

3.1 快速傅里叶变换

离散傅里叶变换在计算机科学、物理学等学科中扮演着非常关键的角色。对于长度为N的复数序列x，其中x=x0,x1,…,xn-1，DFT的计算公式[9]为：

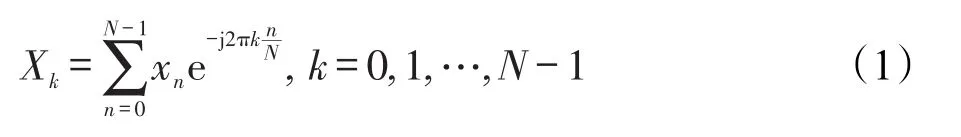
根据式（1），可以发现Xk共有N次输出结果，每一次的输出都有N次的累加求和运算，若按照DFT的定义进行计算求值需O(n2)次运算。在实际应用中，FFT算法通常被用于DFT变换。原因有两点：一是FFT算法在求解过程中会有舍入误差的存在，因此许多FFT算法运行后的结果甚至比用定义进行求解的结果要精确很多；二是FFT算法的运算速度更快，所有的FFT算法的复杂度均可在对数时间复杂度内完成[10]。FFT已经有很多成熟的算法，在所有的FFT算法中，库利图基算法应用最广、最流行，是众多算法库实现的基础，故下文将简要地介绍库利图基算法。

3.2 库利图基快速傅里叶变换算法

库利图基快速傅里叶变换算法（Cooley-Tukey算法）[11]是目前应用最广泛、最流行的FFT算法。利用式（1），将公式中的项目在时域上进行重新分组，并将进行替换，其中替换后的被称为“旋转因子”（twiddle factor），亦称为“蝶形因子”。根据旋转因子在计算过程中出现的不同位置，可以将FFT算法分为时域抽取（decimation-in-time，DIT）和频域抽取（decimation-in-frequency，DIF）两大类。DIT的旋转因子出现在计算的输入端，而DIF的旋转因子则出现在计算的输出端。

以DIT为例，将旋转因子替换后，DIT是将长度为N的复数序列x根据数据的偶数项和奇数项进行分解，分解后的式（1）将成为偶序列与奇序列两部分。其中偶序列为x0,x2,x4,…,xn-2，奇序列为x1,x3, x5,…,xn-1，运算如式（2）：

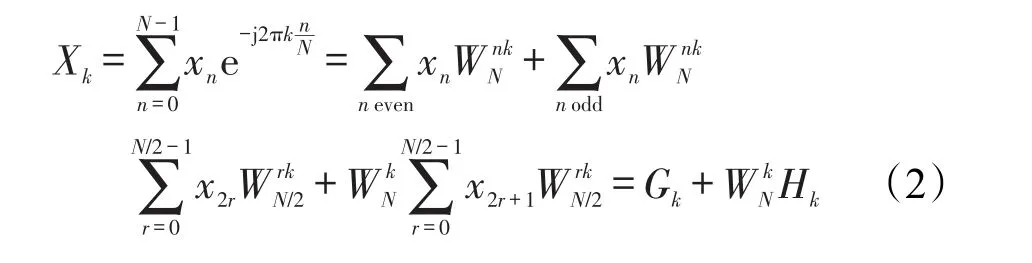
其中k=0,1,…,N-1。

因为Gk与Hk具有周期性，WN具有对称性和周期性，所以可得：

按照同样的方式，对式（3）中的Gk与Hk也继续以相同的方式分解，则可将一个N点的离散傅里叶变换最终用一组两点的DFT来计算。在基数为2的快速傅里叶变换中，共有lbN级运算，而且在每一级的计算中有(N/2)个两点FFT蝶形运算[12]。因此采用该FFT算法的复杂度将直接降为O(nlbn)。

4 并行FFT优化分析及策略

4.1 优化分析

对于许多应用，FFT算法的输入并不能完全只在一个单节点上进行，因此对输入数据势必要划分到各个节点上运算以提高效率。每个子任务计算自己的FFT部分，之后再将数据与其他子任务进行交换。实现该操作的策略有一维分解和二维分解。

对于异构平台上的应用，一个比较普遍的问题是哪一种任务适于使用GPU设备进行加速。GPU适合处理计算密集型或者访存密集型的任务，其他任务，例如Internet带宽，存储设备的读、写带宽以及通信延迟等都是不能被GPU加速的。

对于小规模的FFT，如果数据能够被全部地置于GPU设备上，那么此时的计算就会从设备内存的高带宽中受益。这种方案是有特定情景的，即大部分的数据都置于设备的内存上，并且FFT在这些数据上运算了多次。这时数据在主存和设备内存间的通信开销与GPU的计算时间相比就可以忽略了。

然而，对于大规模的FFT，数据需要在主存和设备内存间不断通信，PCI-E总线带宽就会成为瓶颈。因为此时通过PCI-E总线的数据传输时间要比在GPU的计算时间长得多。这种方案也是有特定情景的，即针对的是在节点上计算大规模FFT，所有数据必须在不同的节点之间、在主存和设备内存之间来回传输的时候，如果能对各节点间的通信、GPU与CPU间的通信进行优化，将会大幅提高整体的计算效率。

4.2 优化策略

4.2.1 一维分解

一维分解是基于转置的并行FFT分解策略，该分解策略已在FFTW算法库[8]中实现。以三维输入数据为例，假设三维的输入数据大小n0×n1×n2，其中n0≥n1≥n2。假定MPI进程的数量为P，则首先沿着n0方向进行分解，将数据切分到P个MPI进程上，这P个进程并行地计算n0/P组大小为n1×n2的二维FFT。此时，n0维的数据已被切分分布于所有的P个进程上，故n0维数据的计算需使用AlltoAll的MPI函数对数据交换转置以完成n0维数据的计算[2]。

MPI_ALLTOALL函数是对MPI_ALLGATHER的扩展，两者的区别是调用MPI_ALLTOALL时每个接收者可接收来自别的发送者的数目不同的数据。例如，第m个进程发送的第n块数据将被第n个进程接收并存放在其接收消息缓冲区recv_buffer的第m块上。

一维分解较为简单，然而采用该策略进行实现的库在可扩展性方面存在很大的不足，它要求P=n0，n0=max{n0,n1,n2}。当P>n0时，一维分解将不能被使用。另外当P>n1或P>n2时，数据分解所使用的进程数P将受限于n1或n2。数据转置之后，多余的进程数将会空闲得不到利用。因此，对数据的划分需要采用更多维来进行计算[4]。图1为一维分解示意图。

Fig.1 One-dimension decomposition strategy图1 一维分解策略

4.2.2 二维分解

二维分解[3]相较于一维分解很好地解决了可扩展性不足这一严重的弊端，故在大规模集群上也应用得比较普遍。图2即为二维分解的效果图。该分解策略首先由Ding等人提出，后来Eleftheriou等人引入了体区域分解（volumetric domain decomposition）的概念，其在本质上使用的还是二维分解，即将输入数组首先沿n0和n1进行分解，因此这种分解策略允许增加的MPI进程数目最多可达n0×n1。因为输入的数据仅有一维数据位于本地进程中，所以每次变换需进行多次的数据交换转置，包括本地的数据转置和全局的数据转置。

Fig.2 Tow-dimension decomposition strategy图2 二维分解策略

对于规模为n0×n1×n2的输入，二维分解会将其并行地分布于P=P0×P1个进程上，每个进程首先会得到大小为n2的二维条，图3表示的就是将输入数据分布到4×4的进程网格上。为了计算三维FFT，算法将沿着n2维进行一批FFT计算，之后进行全局转置操作，以使得每个进程在本地得到第二维的数据。类似的操作会再次进行以得到第一维的数据，最终的输出分布形式为此时输出的内存排列与输入时是不一致的，差别为输入数组沿着第一和第二个维度分布，而输出数组则沿着第二和第三维度分布，如图4所示。PFFT、MPFFT算法在此之后会在输出数组上进行内存布局的调整，以使最后的输出维度的分布也与输入时一致。

Fig.3 Input data distributed on 16 processes initially(4×4 process grid)图3 初始时输入数据分布于16个进程上（4×4进程网格）

Fig.4 Input data distributed on 16 processes at the end(4×4 process grid)图4 结束时输入数据分布于16个进程上（4×4进程网格）

4.2.3 通信优化

基于上面的分解策略，FFTW库采用了一维分解，PFFT和MPFFT库采用了二维分解。FFTW和PFFT算法未进行通信方面的优化。MPFFT算法在每维FFT计算时直接调用NVIDIA CUFFT库，之后进行本地转置，由于此时转置所需的数据全部位于GPU中，故其是借助GPU上的矩阵转置函数来提高性能。之后与CPU通信时的全局转置是通过封装FFTW中相关接口直接实现，并未进行更进一步的优化。而在大规模计算FFT时，显然这将会成为一个限制效率的瓶颈。

基于此可以考虑将需要传送拷贝的数据划分为相同大小的数据块[13]。通过异步通信的方式，一次将一个数据块拷贝到CPU内存中，此时CPU间的通信便可以开始，同时其他的数据块也以异步的方式传输到CPU内存。也可以调用异步接收指令，这样数据接收操作与数据块从设备向主存的拷贝操作同时进行。同时，每个接收的数据块之后可以异步地拷回到GPU设备中，这样便可有效地提高通信效率，减少全局转置所需的时间。图5展示了对于P=4时all-to-all的过程。4×4矩阵中的每个元素代表了存储的数据块。表示从进程i到进程j的一个发送指令，表示进程j接收来自进程i的消息。

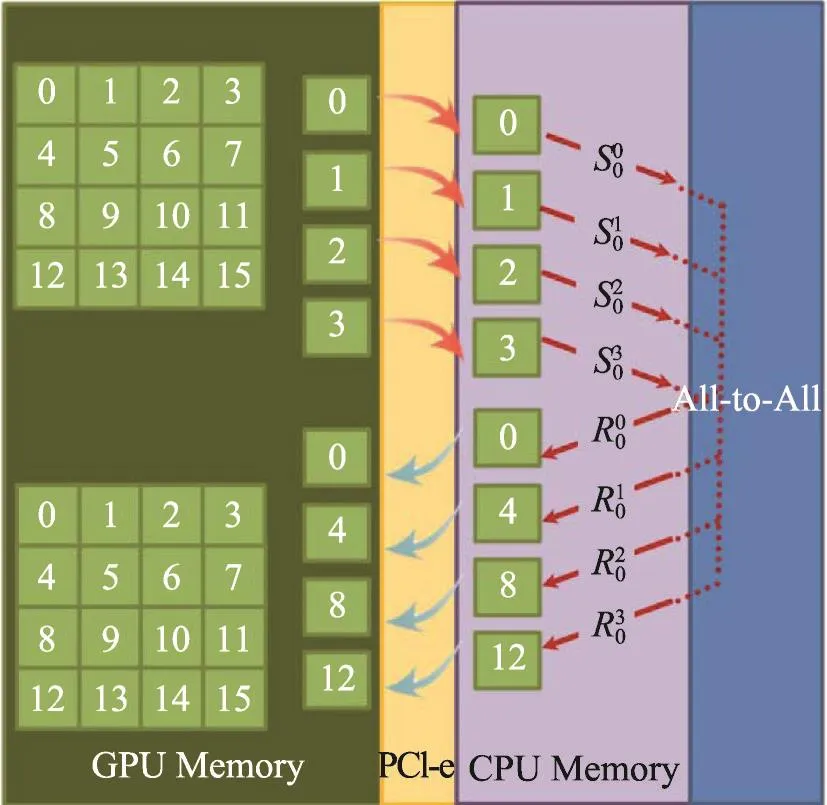
Fig.5 Communication optimization图5 通信优化示意图

4.2.4 输出优化

假设用T0代表本地转置，用T1代表全局转置，以0代表经FFT计算后的n0。在运算过程中，初始的输入分布可表示为采用二维分解策略，经过一系列计算后得到的输出分布为此后，一部分FFT算法，例如PFFT、MPFFT算法，将在此输出形式上进行多次转置计算以改变其内存布局[14-15]，转换过程可表示如下：

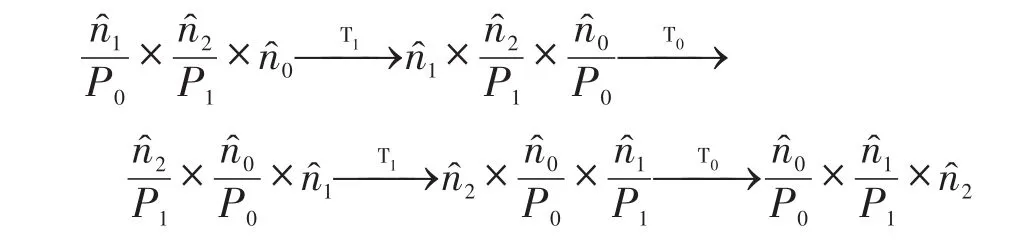
经过多次的本地转置和全局转置，可以将输出的分布形式完全转化为和初始的输入分布一致，即为然而这种转化是在已经得到正确的输出结果之上所做的进一步的整理工作，这种额外的数据整理又会增加一些计算和通信上的开销，而这种开销理论上也可以进行进一步的分析优化。在不可避免使用全局转置的地方尽量以块划分的异步通信策略进行优化，而在每一维度上进行转置来计算FFT的时候可以进行更为细致的粒度划分，即在每一块数据进行FFT计算的同时确定好最优的内存分布位置，便于对计算后的数据进行排列。这样，便可以在FFT计算的同时进行数据整理，减少额外进行转置的开销。另外，在某些不需要得到和输入相同数据分布的输出的情况下，对输出数据的整理就是一步冗余操作。此时可以直接取消输出转化的过程，输出计算后的结果或按实际需求相应地进行小规模的数据整理，这也可以减少算法运行的时间。

5 性能评估

本文对FFTW、PFFT和MPFFT库在异构单节点、天河一号和天河二号3种平台上的性能和可扩展性进行评估，其中FFTW库的版本为3.3.4，具体测试评估将分别进行介绍。

5.1 单节点上算法性能分析

本节将在固定的异构平台A上分别对FFTW、PFFT以及MPFFT算法进行常规测试。

本次实验平台A为CPU和GPU的异构平台，其中CPU配置的详细信息如表1所示。平台上共有3块GPU，分别是一块GeForce GTX Titan Black，内存为6 GB；两块Tesla K80，内存均为11 GB。使用的CUDA版本为7.5，且运行时调用了3块GPU进行计算。

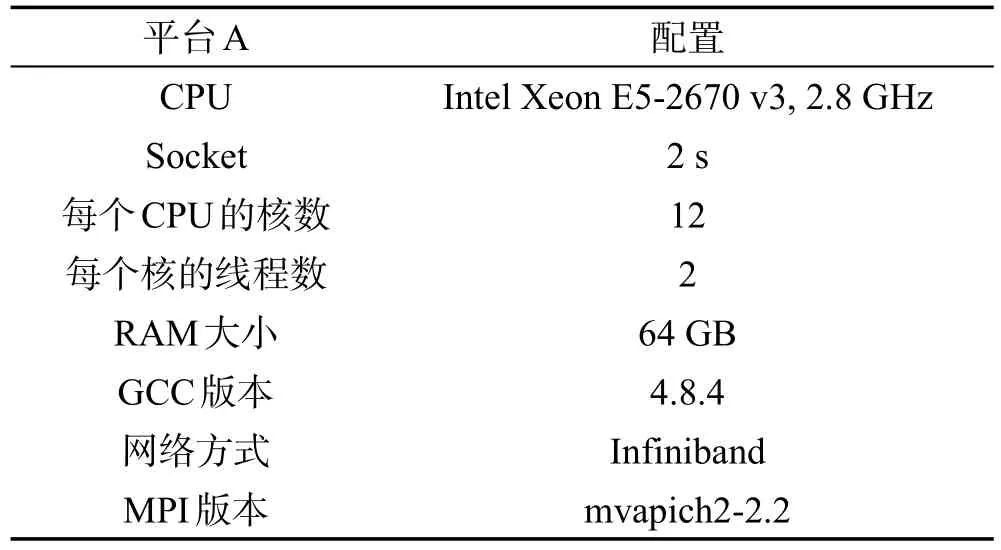
Table 1 CPU configuration表1CPU配置信息

实验分为两种输入：一是1 024×1 024×1 024的规模下，采用FFTW和PFFT算法得到的性能；二是输入规模为256×256×256，采用FFTW、PFFT和MPFFT算法得到的性能。具体实验所得数据如图6~图10所示。

图6和图7为1 024×1 024×1 024的输入时，采用FFTW和PFFT算法得到的性能。从中可以看出PFFT比FFTW算法可扩展性更强，当输入为1 024×1 024× 1 024时，其性能一直优于FFTW算法。随着进程数量的增加，算法性能也在增长，但由于该平台是单节点服务器，该测试并未能真正体现出在大规模集群上的运行情况。另外平台中GPU内存大小的限制使得MPFFT算法不能够接收如此大规模的输入。

针对GPU内存大小的限制问题，本文使用256× 256×256的输入在该平台上进行新的测试，图8和图9即为测试结果。整体上看，3种算法的运算性能大致为MPFFT优于PFFT优于FFTW算法，且3种算法的运算性能随进程数量的增加都在提升。更确切地说，在并行的进程数小于8时，使用GPU的MPFFT异构算法和使用并行计算的PFFT算法要优于FFTW算法，而随着进程数量的增加，两种算法相对于FFTW算法的优势则不再明显。主要原因可归为以下3点：

（1）随着进程数量的增加，并行算法中进程间的通信和数据交换将明显地影响到算法的性能。

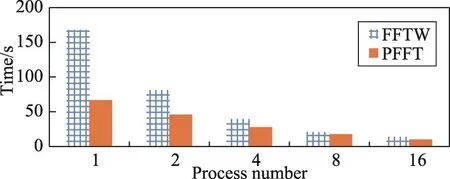
Fig.6 Running time comparison of different algorithms when input size is 1 024×1 024×1 024(PlatformA)图6 数据规模为1 024×1 024×1 024时不同算法运行时间对比（平台A）

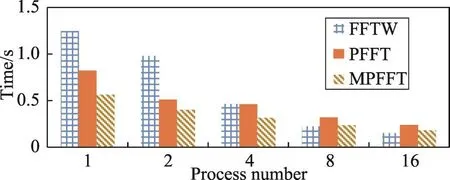
Fig.8 Running time comparison of different algorithms when input size is 256×256×256(PlatformA)图8 数据规模为256×256×256时不同算法运行时间对比（平台A）

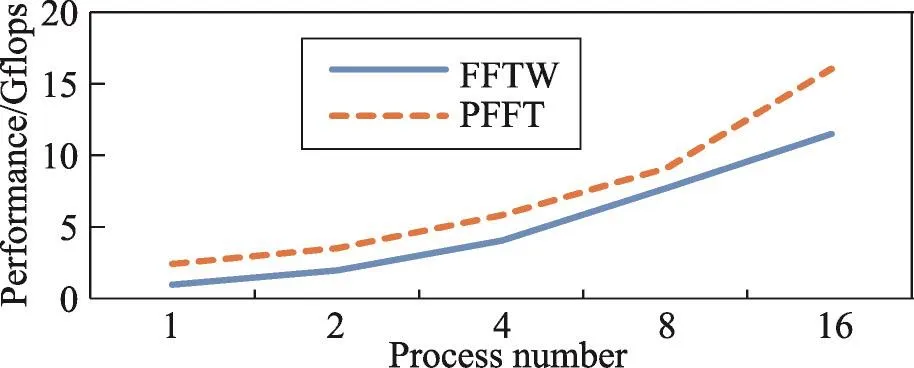
Fig.7 Performance comparison of different algorithms when input size is 1 024×1 024×1 024(PlatformA)图7 数据规模为1 024×1 024×1 024时不同算法运行性能对比（平台A）

Fig.9 Performance comparison of different algorithms when input size is 256×256×256(PlatformA)图9 数据规模为256×256×256时不同算法运行性能对比（平台A）

（2）PFFT与MPFFT算法针对的都是集群优化的算法，平台A只是一个单节点服务器，故当进程数量、输入量较小时，在并行和GPU方面进行优化的MPFFT算法与PFFT算法会大幅地改善性能。

（3）当进程数量逐渐增加，此时测试的数据与之前的大规模输入相比较小，因此计算任务比之前要小，在这种情况下GPU的加速性能并没有充分利用，使得优化效果减弱，且较小规模的计算任务时PFFT算法的可扩展性将不如FFTW算法，从而当进程增加时MPFFT算法与PFFT算法的总体性能将会出现暂时不如FFTW算法的现象。

图10为1 024×1 024×1 024与256×256×256的输入时各FFT算法在平台A上的加速情况对比。据图可知，各算法在接收大输入数据量时加速比率要高于接收小输入数据量时的加速比率，并且FFTW的加速效果较优，MPFFT的加速效果较差。原因可归为两点：

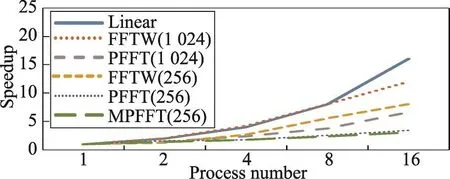
Fig.10 Speedup comparison of different algorithms when input size is 1 024×1 024×1 024 and 256×256×256(PlatformA)图10 数据规模为1 024×1 024×1 024与256×256×256时不同算法加速情况对比（平台A）

（1）各算法在接收大规模数据输入时的性能表现能较好地排除接收小规模数据时所产生的偶然性，更能反映出其真正的性能情况，并且PFFT与MPFFT算法针对接收大规模数据时的操作进行了相关的优化。

（2）PFFT与MPFFT算法由于进行了优化，使得其在较小进程数时已产生相对FFTW较高的性能，而随进程数升高，上述分析已说明其优化效果将受平台环境的制约而减弱，故其加速情况也将受影响而小于FFTW的加速比。

5.2 大规模集群上算法性能分析

本节探讨的是在大规模集群上的FFT算法测试。针对平台A是单节点服务器不能进行大规模集群上的运算从而无法获得算法可扩展性的问题，本文使用了平台B——天河一号超级计算机（TH-1A）。

TH-1A以持续性能每秒2 507万亿次列世界超级计算机排名第五位，其配备了14 336颗至强X5670处理器、7 168块基于英伟达的Tesla M2050计算卡、2 048颗国防科大的飞腾处理器以及5 PB存储设备。

本文使用了256×256×256、512×512×512、1 024× 1 024×1 024的输入数据分别在TH-1A上进行测试，且每个节点进行多个进程的并行计算获得如下结果。

由于GPU的内存大小限制，MPFFT算法不能在TH-1A上接收输入数据规模为512×512×512及以上的输入。图11、图12分别是输入为1 024×1 024× 1 024和512×512×512时FFTW与PFFT算法运行时间对比。由图可以分析出，在大规模集群上接收512×512×512及以上规模的输入数据时，PFFT算法耗时始终要少于FFTW算法，且进程数量达到256及以上时FFTW算法的性能将达到瓶颈，而PFFT算法至多可扩展到2 048个进程上继续进行计算，且性能也在不断提升。

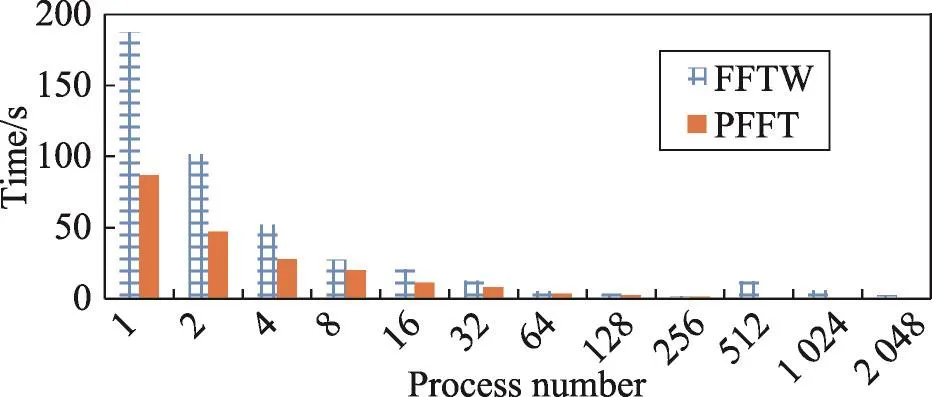
Fig.11 Running time comparison of different algorithms when input size is 1 024×1 024×1 024(TH-1A)图11 数据规模为1 024×1 024×1 024时不同算法运行时间对比（TH-1A）

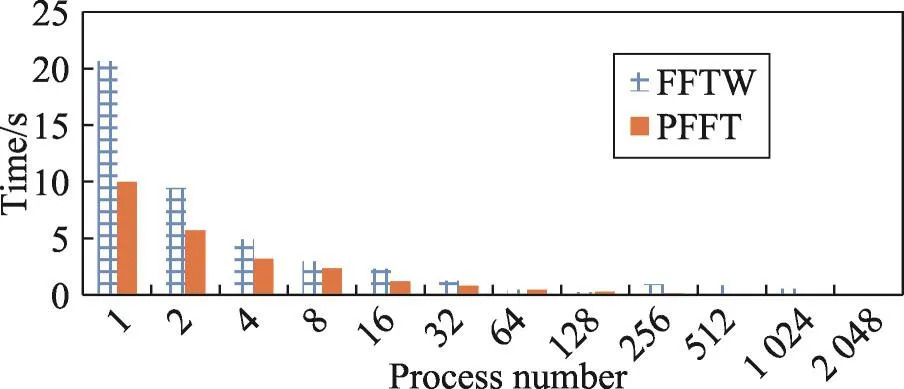
Fig.12 Running time comparison of different algorithms when input size is 512×512×512(TH-1A)图12 数据规模为512×512×512时不同算法运行时间对比（TH-1A）

图13展示了FFTW与PFFT算法在接收512× 512×512和1 024×1 024×1 024的输入数据时的性能对比。对比表示，在进程数量较少时，同一种算法在接收不同规模的输入时性能差异不大，并且PFFT相对于FFTW算法的优势也不明显；然而，PFFT算法的性能在接收1 024×1 024×1 024的输入反而比接收512×512×512的输入要高很多，且随着进程数量的增加性能优势越明显。主要原因为PFFT算法的设计考虑到了多进程上的并行优化，所以输入数据量越大，使用的进程数量越多，利用PFFT算法进行优化计算得到的效果就越明显。这充分说明了PFFT算法在大规模输入多进程上的可扩展性非常强。另外，FFTW算法在使用多进程计算时优化性能至多支持到256个进程，且在接收亿级输入数据时在256个进程上已经开始出现明显的性能下降现象，这也说明了FFTW算法在多进程上的可扩展性不高。

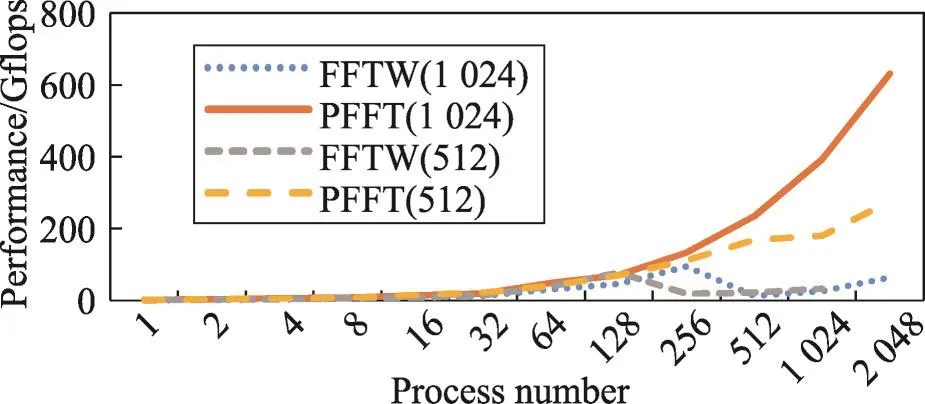
Fig.13 Performance comparison of different algorithms when input size is 1 024×1 024×1 024 and 512×512×512(TH-1A)图13 数据规模为1 024×1 024×1 024和512×512×512时不同算法运行性能对比（TH-1A）

图14与图15分别是在接收256×256×256输入数据量时3种算法的运算时间对比和性能对比。由图分析可知，在进程数量较小的情况下，MPFFT算法性能优势明显；随着进程数量的增多，在进程数小于64时，3种算法的性能相差不大；当FFTW算法运行的进程数大于32，MPFFT算法运行的进程数大于128时，FFTW与MPFFT算法的性能都开始呈下降趋势，且这两种算法随着进程数的翻倍增长性能却没有明显的增长，而此时PFFT算法仍有较好的性能。

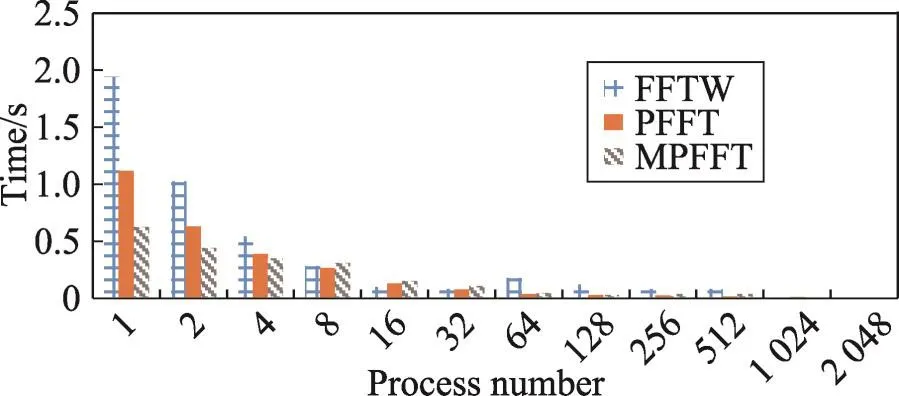
Fig.14 Running time comparison of different algorithms when input size is 256×256×256(TH-1A)图14 数据规模为256×256×256时不同算法运行时间对比（TH-1A）

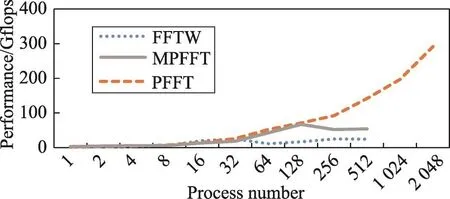
Fig.15 Performance comparison of different algorithms when input size is 256×256×256(TH-1A)图15 数据规模为256×256×256时不同算法运行性能对比（TH-1A）

综合分析，MPFFT算法主要是针对异构平台上的FFT进行优化，当数据量较小，不断增大进程数时，计算时间上的减小不再明显，相对于较小的数据计算时间，增加的节点间的通信以及多个GPU的启用时间会使得整体的性能下降；PFFT算法着重多进程上的并行优化和改进，当进程数量增加时其优化效果将会逐渐显露；而FFTW算法并未有上述两种算法的优化，故进程数渐增，MPFFT算法优化性能开始下降而PFFT算法优化性能效果还不明显的时候，其将会有稍优于MPFFT与PFFT算法的性能表现。

图16为在接收256×256×256、512×512×512和1 024×1 024×1 024输入数据量时各FFT算法的加速情况对比。为了使加速情况对比更为清晰，图中横轴使用的是以2为底进程数的对数，纵轴使用的是以2为底加速比的对数。在线性加速比的对比下，各加速算法在接收更大规模输入数据时的加速比是相对更高的，这也印证了之前分析的正确性。未经优化的FFTW算法随着进程数增加其加速比呈现了波动的趋势，而PFFT和MPFFT算法的波动相对要小得多。其中，以接收输入数据量为1 024×1 024×1 024时PFFT算法加速比最稳定且最贴近线性加速比，说明PFFT算法在大规模计算时的扩展性还是较高的。

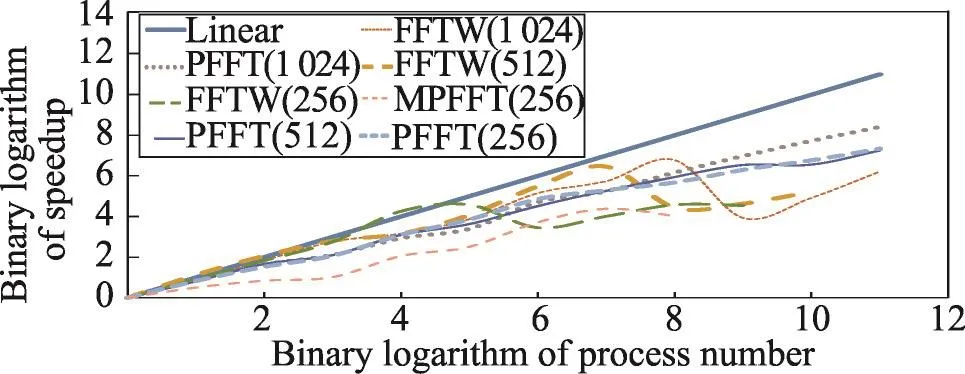
Fig.16 Speedup comparison of different algorithms under different input size(TH-1A)图16 多种输入数据规模下不同算法加速情况对比（TH-1A）

之所以出现加速比波动的情况，主要原因为随着进程数不断地呈两倍提升，额外带来的通信开销却将并行效果相应地弱化，两倍的计算资源不但不能提供两倍的加速效果，反而还会带来性能的降低。

图17为3种FFT算法在TH-1A上的性能评估。横轴使用以2为底进程数量的对数值来表示进程的规模，纵轴使用的是以2为底输入数据第一维度的对数值来表示输入的规模。气泡的大小代表在指定的进程数量和指定的输入规模下的性能值，气泡越大，在该环境下的性能越好，反之则越差。

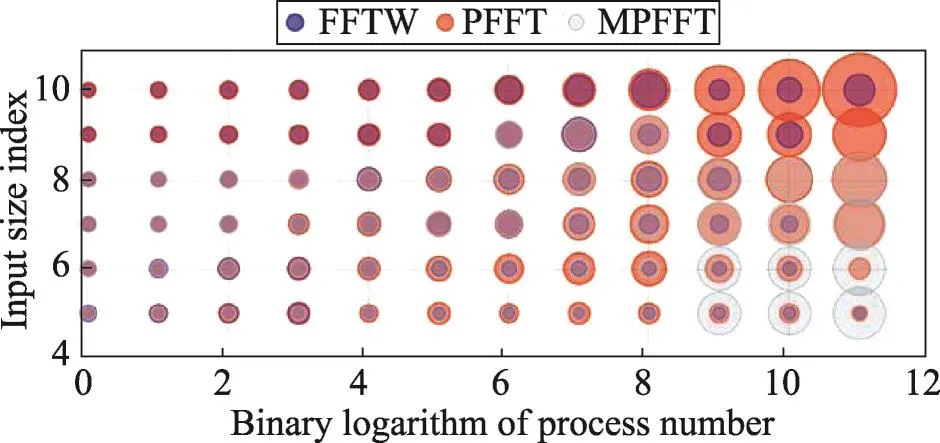
Fig.17 Performance evaluation of different algorithms on TH-1A图17 天河1号不同算法性能评估

由图17可分析得知，在大多数的情况下PFFT算法与MPFFT算法要优于FFTW算法，且当输入数据量较小时，MPFFT算法性能优势相对明显；输入数据量较大时，PFFT算法性能优势则相对明显。另外，这种性能优势会随着进程数量的增加而更为突出，当进程数量较小时，3种算法的性能优劣对比并不明显。

5.3 大规模集群上算法性能分析

本节探讨的是单一平台（CPU）下的大规模集群上的FFT算法测试。在天河一号上的运行环境是异构平台多进程，而在本节中将使用天河二号超级计算机（TH-2）来重点评估多节点上的PFFT算法运行情况。

天河二号是由国防科技大学研制的异构超级计算机，共有16 000个运算节点，每个节点配备两颗Xeon E5 12核心的中央处理器，3个Xeon Phi 57核心的协处理器。本文采用了PFFT算法进行测试以分析其可扩展性。实验中，为了更准确地对算法在大规模集群上的性能进行测量，在每个节点上均指定运行一个进程，输入数据量为1 024×1 024×1 024。

数据结果如图18和图19所示，每个节点上运行一个进程，申请的最大节点数为256，因此该数据可以真实有效地反映在大规模集群上FFT算法的性能情况。从图中可以看出，随着节点数的增加，PFFT算法的性能也在逐步地提升，且加速比大致符合线性加速比，实际的加速情况与理想加速情况的最大差距不超过16%（16节点时）。因此，该数据可证明在大规模集群上（256节点）PFFT算法有着较为理想的加速实现，即该算法在多节点上的优化已较为理想。

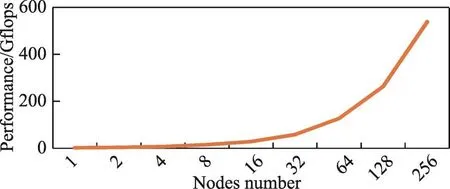
Fig.18 Performance evaluation of PFFT algorithm when input size is 1 024×1 024×1 024（TH-2）图18 数据规模为1 024×1 024×1 024时PFFT算法运行性能（TH-2）

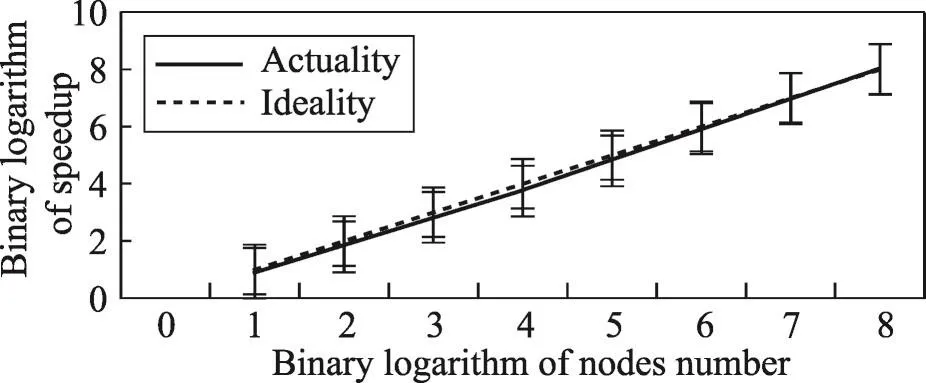
Fig.19 Speedup comparison of PFFT algorithm when input size is 1 024×1 024×1 024（TH-2）图19 数据规模为1 024×1 024×1 024时PFFT算法加速情况对比（TH-2）

6 总结

多维FFT最终都是转换成一维FFT来计算，目前分布式FFT算法主要有一维切片分解和二维束分解[14]。前者可扩展性比较差，目前只能应用于小规模的集群系统上。而后者需要在计算中穿插更多的全局转置和本地转置，计算过程相对比较复杂。

本文针对CPU和GPU的异构集群系统，研究了多维FFT并行算法进一步的优化方法，从通信和输出等方面提出的优化策略可为现行FFT算法的改进提供参考。在此基础上在不同的平台上对3种FFT算法进行了全方位的性能评估。性能评估的结果也可以为FFT算法在大规模运算时提供可靠和全面的参考。

[1]SKA Telescope.The square kilometre array SKA home[EB/ OL].[2016-09-28].https://www.skatelescope.org/.

[2]Frigo M,Johnson S G.FFTW:an adaptive software architecture for the FFT[C]//Proceedings of the 1998 International Conference on Acoustics,Speech and Signal Processing, Seattle,USA,May 12-15,1998.Piscataway,USA:IEEE, 1998:1381-1384.

[3]Pippig M.PFFT:an extension of FFTW to massively parallel architectures[J].SIAM Journal on Scientific Computing, 2013,35(3):C213-C236.

[4]Li Yan,Zhang Yunquan,Liu Yiqun,et al.MPFFT:an autotuning FFT library for OpenCL GPUs[J].Journal of Computer Science and Technology,2013,28(1):90-105.

[5]Nvidia C.CUFFT library[DB].2010.

[6]Chen Yifeng,Cui Xiang,Mei Hong.Large-scale FFT on GPU clusters[C]//Proceedings of the 24th International Conference on Supercomputing,Tsukuba,Japan,Jun 2-4,2010.New York:ACM,2010:315-324.

[7]Cui Xiang,Chen Yifeng,Mei Hong.Improving performance of matrix multiplication and FFT on GPU[C]//Proceedings of the 15th International Conference on Parallel and Distributed Systems,Shenzhen,China,Dec 8-11,2009.Washington:IEEE Computer Society,2009:42-48.

[8]Pippig M.PFFT user manual.2014.

[9]Frigo M,Johnson S G.The design and implementation of FFTW3[J].Proceedings of the IEEE,2005,93(2):216-231.

[10]Bracewell R N.The Fourier transform and its application[M]. 3rd ed.New York:McGraw-Hill,1999.

[11]Cooley J W,Tukey J W.An algorithm for the machine calculation of complex Fourier series[J].Mathematics of Computation,1965,19(90):297-301.

[12]Cooley J W,Lewis P A W,Welch P D.Historical notes on the fast Fourier transform[J].IEEE Transactions on Audio &Electroacoustics,1967,15(2):76-79.

[13]Gholami A,Hill J,Malhotra D,et al.AccFFT:a library for distributed-memory FFT on CPU and GPU architectures[J]. arXiv:1506.07933v2,2015.

[14]Li Yan,Zhang Yunquan,Jia Haipeng,et al.Automatic FFT performance tuning on OpenCL GPUs[C]//Proceedings of the 17th International Conference on Parallel and Distributed Systems,Tainan,China,Dec 7-9,2011.Washington:IEEE Computer Society,2011:228-235.

[15]Liu Yiqun,Li Yan,Zhang Yunquan,et al.Memory efficient two-pass 3D FFT algorithm for Intel®Xeon PhiTM,coprocessor[J].Journal of Computer Science and Technology, 2014,29(6):989-1002.

LI Kun was born in 1992.He is a Ph.D.candidate at University of Chinese Academy of Sciences.His research interests include high performance computing and parallel software,etc.

李琨（1992—），男，山东青岛人，中国科学院计算技术研究所博士研究生，主要研究领域为高性能计算，并行软件等。

贾海鹏（1983—），男，山东潍坊人，2013年于中国海洋大学获得博士学位，现为中国科学院计算技术研究所助理研究员，主要研究领域为异构计算，多核并行编程方法，多核上的计算机视觉算法等。

CAO Ting was born in 1984.She received the Ph.D.degree in computer system from The Australian National University in 2014.Now she is a post-doctor at Institute of Computing Technology,Chinese Academy of Sciences.Her research interests include high-level language implementation,novel computer architecture design,hybrid memory management and high performance computing,etc.

曹婷（1984—），女，辽宁抚顺人，2014年于澳大利亚国立大学获得博士学位，现为中国科学院计算技术研究所博士后，主要研究领域为高级语言实现，新型计算机体系结构设计，异质内存管理，高性能计算等。

ZHANG Yunquan was born in 1973.He received the Ph.D.degree in parallel software from Institute of Software, Chinese Academy of Sciences in 2000.Now he is a professor and Ph.D.supervisor at Institute of Computing Technology,Chinese Academy of Sciences.His research interests include high performance parallel computing,with particular emphasis on large scale parallel computation and programming models,high-performance parallel numerical algorithms,performance modeling and evaluation for parallel programs,etc.

张云泉（1973—），男，山东聊城人，2000年于中国科学院软件研究所获得博士学位，现为中国科学院计算技术研究所研究员、博士生导师，主要研究领域为高性能并行计算，尤其是大规模并行计算及编程模型，高性能并行数值算法，并行程序的性能建模和评估等。

Implementation and Optimization of Multidimensional FFT Algorithm on Large-Scale Clusters*

LI Kun1,2+,JIAHaipeng1,CAO Ting1,ZHANG Yunquan1
1.State Key Laboratory of Computer Architecture,Institute of Computing Technology,Chinese Academy of Sciences, Beijing 100190,China
2.School of Computer and Control Engineering,University of ChineseAcademy of Sciences,Beijing 100190,China +Corresponding author:E-mail:likun@ict.ac.cn

Fast Fourier transform(FFT)is a fast algorithm which computes the discrete Fourier transform(DFT)of a sequence,or its inverse.Fast Fourier transform is widely used for many applications in engineering,science and mathematics,such as signal decomposition,digital filter and image processing.As a result,the fine-grained optimization of FFT is extremely important in application.This paper studies the typical decomposition strategies of FFT, the parallel implementation of FFT algorithms on large-scale clusters and proposes some optimization strategies.Onthat basis,this paper also evaluates a variety of FFT algorithms performance on different platforms,then analyzes the implementation,strength and weakness,and the computing scalability on large-scale clusters of these algorithms. The experimental results show that the research of this paper can contribute to the further optimization on existing FFT algorithms,and instruct to choose an FFT algorithm which performance is better on large-scale heterogeneous systems(CPU and GPU)in order to satisfy the specified requirements.

cluster;fast Fourier transforms(FFT);message passing interface(MPI);performance optimization

ng was born in 1983.He

the Ph.D.degree in parallel software from Ocean University of China in 2013.Now he is an assistant professor at Institute of Computing Technology,Chinese Academy of Sciences.His research interests include heterogeneous computing,many-core parallel programming method and computer vision algorithms on multi-/many-core processors,etc.

A

TP302.7

*The National Natural Science Foundation of China under Grant Nos.61432018,61133005,61272136,61521092,61502450(国家自然科学基金);the National Key Research and Development Program of China under Grant No.2016YFB0200803(国家重点研发计划);the Postdoctoral Science Foundation of China under Grant No.2015T80139(中国博士后科学基金);the National High Technology Research and Development Program of China under Grant Nos.2015AA01A303,2015AA011505(国家高技术研究发展计划(863计划));the Key Technology Research and Development Programs of Guangdong Province under Grant No.2015B010108006 (广东省科技计划项目);the CAS Interdisciplinary Innovation Team of Efficient Space Weather Forecast Models(中科院高效空间天气预报模式科技创新交叉与合作团队项目).

Received 2016-11,Accepted 2017-01.

CNKI网络优先出版:2017-01-05,http://www.cnki.net/kcms/detail/11.5602.TP.20170105.0828.006.html