路网中线段反k最近邻查询研究*
张丽平,郭莹莹,李 松,李 爽,樊瑞光
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
路网中线段反k最近邻查询研究*
张丽平+,郭莹莹,李 松,李 爽,樊瑞光
哈尔滨理工大学 计算机科学与技术学院,哈尔滨 150080
ZHANG Liping,GUO Yingying,LI Song,et al.Line reverseknearest neighbor query in road network.Journal of Frontiers of Computer Science and Technology,2017,11(6):908-920.
为了弥补现有的研究成果无法有效地处理路网环境下基于线段的反k最近邻问题的不足,提出了在路网环境下线段反k最近邻查询方法。该查询方法主要应用于评估查询对象的影响范围。根据路网及Voronoi图的特点提出了网络线段Voronoi图的概念。在静态数据集情况下利用网络线段Voronoi图的性质提出了STA_RVLRkNN算法,查询包括过滤过程和精炼过程两大部分。进一步,在动态数据集的情况下提出了DYN_ RVLRkNN算法,查询分为空间线段对象增加和删除两种情况,并对不同的情况给出了相应的算法,得到查询结果集。理论研究和实验表明,所提算法能有效地处理路网中基于线段的反k最近邻问题。
路网;网络线段Voronoi图;反k最近邻
1 引言
空间数据库是数据库领域的重要分支,它在许多领域都有着广泛的应用,例如地理信息系统[1]、决策支持系统[2]、交通路网系统[3]等。传统的近邻查询研究主要是在欧式空间环境下进行的,然而相较于欧式空间中的近邻查询而言,在路网环境下的最近邻查询更符合现实生活中的相关应用。路网环境与欧式空间最大不同点在于,在路网中所有的查询点和空间对象都局限在路网的路径上,并且两点之间的最短距离是最短路径和的距离,而在欧氏空间中最短距离为两点的直线距离。
近邻查询是空间数据库中的重要查询类型之一。近邻查询包含多种类型:最近邻(nearest neighbor,NN)查询[4-6]、k最近邻(knearest neighbor,kNN)查询[7-9]、反向最近邻(reverse nearest neighbor,RNN)查询[10-12]、反k最近邻(reverseknearest neighbor,RkNN)查询[13]等。最近邻查询是空间数据库中最为传统的一种查询类型,k最近邻查询是最近邻查询更为一般化的扩展。kNN查询应用的一个常见场景就是,交通道路上的出租车寻找离自己最近的加油站。反k最近邻查询研究类似于人们生活中常遇到的查找影响范围的问题。例如,一家连锁超市在道路网络上的某一地点打算投资一个新的超市点(假设人们在购买商品时一般采取就近原则),那么这必然会对附近同类型的超市带来商业上的影响,而受其影响较大的那些超市,就是反向k最近邻查询的结果。
近年来,在对反k最近邻查询问题的研究中,国内外学者已经提出了多种解决方案。文献[14]针对移动物体延迟更新和隐私保护等问题造成的数据的不确定性给出了有效的解决方法。另外在实际路网中,由于移动数据对象的种类多种多样,单色反向最近邻查询有时并不能完全满足要求。文献[15]通过PMR四叉树索引路网,实现对路网的连续监控。文献[16]提出了一种基于障碍空间的反k最近邻查询方法,利用障碍Voronoi图的高效剪枝方法,大幅度减少了处理点的个数。文献[17]提出了一种基于第三方可靠服务器的方法,确保用户在享受基于位置服务所提供的实际准确答案的同时,其位置信息不被泄露。
在实际生活中探索查询问题时,许多空间对象如果抽象成点进行研究将会对查询结果的精度造成影响。例如,山脉、河流、轨道等在研究过程中都不适合抽象为点。为了提升查询的效果可以将其抽象为线段,因此文献[18]提出了解决平面线段之间的最近邻问题,以及基于线段最近邻的概念和相关查询算法。文献[19]提出了基于移动线段k最近邻查询问题。文献[20]以基于线段的索引结构(SI-树)为基础提出了新的剪枝规则,加快了查询速度。现阶段在路网环境下的近邻研究都是以点为对象进行研究的,没有考虑路网条件下基于线段的近邻研究,且相较于欧式空间而言,路网环境下的研究更贴近人们的生活。因此,本文所提出的路网环境下线段反k最近邻查询问题是一个新的需要解决的问题。例如,在城市中某一大楼发生火灾事故时,为了采取一种最快捷有效的方式处理火灾事故,消防人员可以利用路网环境下线段的反向k最近邻查询技术确定受火灾影响的范围。又如,居民在购买住房选址时,难免会考虑到高速公路或者火车轨道所带来的噪声影响,因此可以通过路网环境下线段的反向k最近邻查询技术判断受噪声影响的范围,更好地选择自己满意的居住位置。
本文所提出的路网中线段反k最近邻查询方法,用于处理不相交的线段。分别讨论了静态数据集和动态数据集两种情况下的线段反k最近邻查询。静态数据集情况下查询分为过滤过程和精炼过程两个阶段。动态数据情况分为数据线段的增加和删除两种情况,通过相对应的算法思想对新的数据线段集进行查询得到新的查询结果集。
2 基础定义与性质
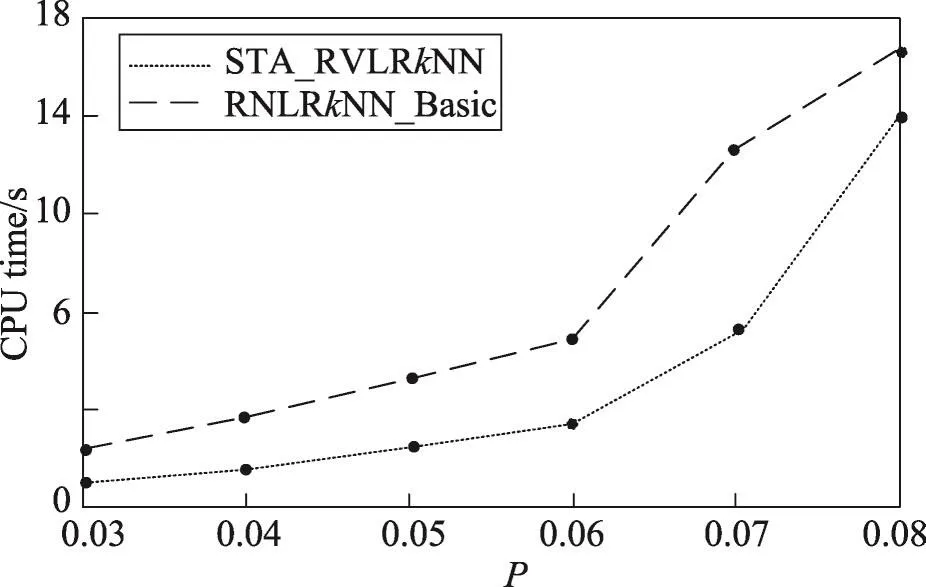
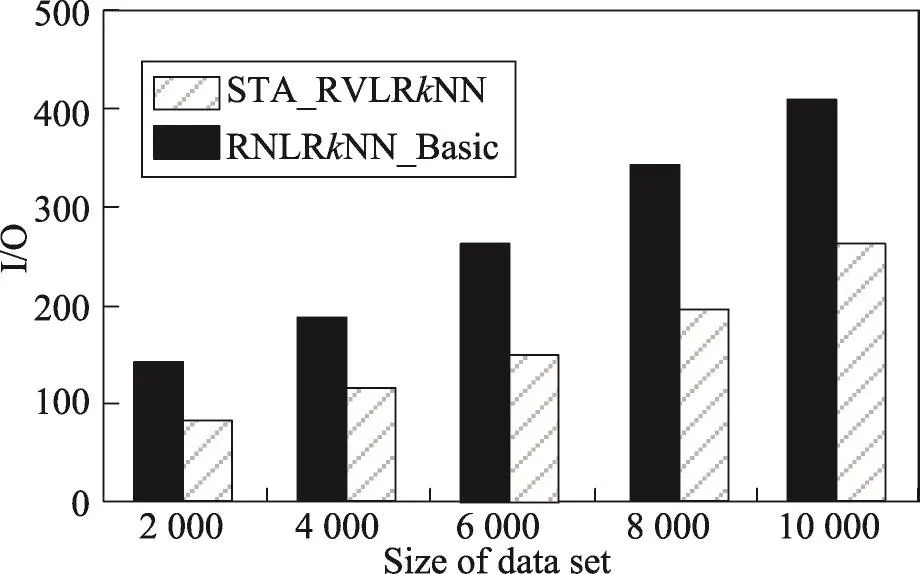
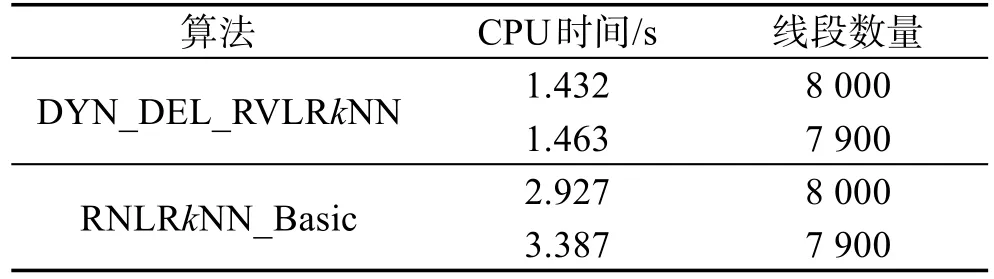
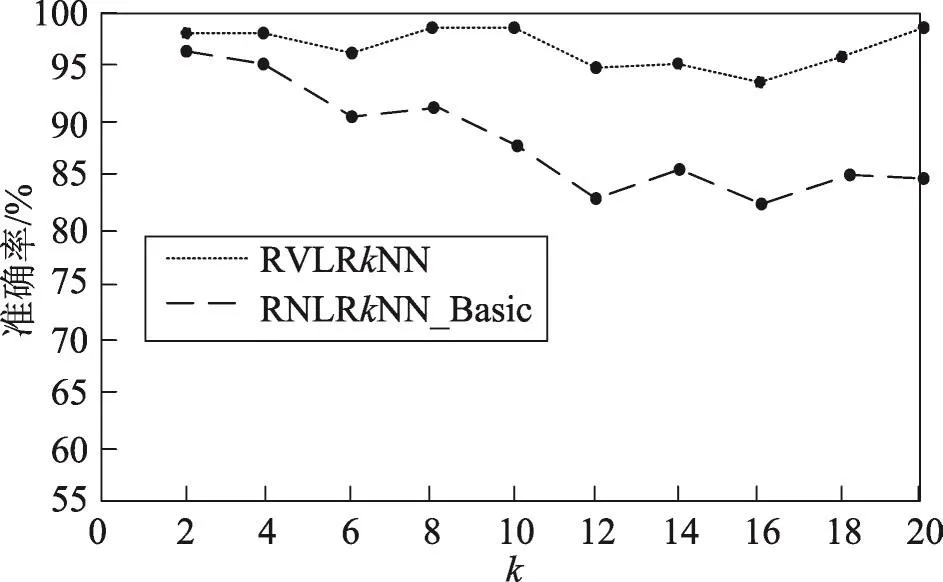
定义1(线段Voronoi图[21])给定一组互不相交的生成线段L={l1,l2,…,ln},每一线段的两个端点已知,其中2 定义2(线段之间的最近距离[18])已知线段L和线段K,点l,li,lj∈L,点k,ki,kj∈K,dist(l,k)表示点l到点k的距离,设线段L与线段K的最近邻距离为dist(L,K)={dist(li,ki),dist(li,ki)≤dist(lj,kj)}。由定理可知,dist(L,K)=dist(K,L)。若两条线段相交,则它们最近距离为0。 定义3(点到线段的最近距离[18])已知点q和线段L,点li,lj∈L,设点q与线段L的最近距离为dist(q,L),则dist(q,L)={dist(q,L)|dist(q,li)≤dist(q,lj)}。 定义4(线段反k最近邻查询)给定一个互不相交线段集L,查询线段lq和一个整数k,在数据集L中找到集合LR,使LR中的线段到lq的距离小于到L中其他任意线段的距离,则称LR为lq的线段反k最近邻,具体定义形式如下: LRkNN(LR)={li|li∈LR,1≤i≤k,d(li,lq)≤d(li,lj)} 进一步,本文所提出的网络线段Voronoi图(network line Voronoi diagram,NLVD)如定义5所示。 定义5(网络线段Voronoi图)给定一组互不相交的生成线段集合L={l1,l2,…,ln},节点集合N={n1,n2,…,ni},边的集合E={e1,e2,…,ek}。假设lj为不同于li的生成线段,网络线段Voronoi图将平面分成若干区域,线段li所在的区域称为NLVP,则NLVP(li)可以形式化定义为: 若线段集L中的每一个线段都能生成一个NLVP,则NLVD由n个NLVP组成,因此可以定义NLVD如下: NLVD(L)={NLVP(l1),NLVP(l2),…,NLVP(ln)} 由网络线段Voronoi图的结构及定义可以得出以下性质。 性质1(最短距离特性)两线段之间的最短距离是线段到边界点的最短距离之和,而非两线段之间的连线距离。 性质2(最近邻特性)生成线段li的最近邻必定存在于与NLVP(li)邻接的NLVP中。 根据网络线段Voronoi图的定义及性质,进一步给出NLVD生成算法如算法1所示。 算法1Create_NLVD 输入:数据线段集L,边的集合E,节点集合N 输出:NLVD Begin 1.根据数据线段集生成线段Voronoi图; 2.设生成线段l的左右端点分别为s、e; 3.过节点n做l的垂线,垂足为o; 4.ifo∈lithen 5.d(ni)=d(ni,o); 6.elseo∉li 7.d(ni)=min{d(ni,s),d(ni,e)}; 8.end if 9.ifd(ni,li)<d(ni,lj) 10.ni∈NLVP(li); 11.end if 12.for each(ni,nj)∈E 13. if(li∩lj=NULL)then 14. 计算NLVP(li)与NLVP(lj)边界点b=(ni,nj|d(ni)-d(nj)-d(ni,nj)/2)的位置; 15. end if 16.end for 17.return NLVD; End Create_NLVD算法的具体过程为:首先利用给定的数据线段集生成线段Voronoi图,通过计算确定节点和边界点的位置。计算节点ni到线段li的最短距离,从而得出ni的最近生成线段以及d(ni)。然后通过比较最短距离,可以确定ni存在于其最短生成线段所在的NLVP中。进一步根据计算公式得出NLVP(li)与NLVP(lj)的边界点位置。继续运行算法得到n个NLVP,从而得到NLVD。 根据线段集中的线段是否变化,本文提出路网中线段反k最近邻查询(RVLRkNN查询)方法。主要分为两部分,分别为静态数据集情况下的RVLRkNN查询(STA_RVLRkNN查询)和动态数据集情况下的RVLRkNN查询(DYN_RVLRkNN查询)两类。 3.1 静态数据集情况下RVLRkNN查询 本节提出的路网中线段反k最近邻查询方法主要包括两个阶段,分别为过滤过程和精炼过程。首先是过滤过程,对查询线段集进行优化处理,获取较精确的候选集。然后是精炼过程,对候选集进行精炼得到更加精确的候选集。最后排除错误结果,得到正确的查询结果集。 3.1.1 过滤过程 过滤过程的主要工作是对查询线段进行过滤处理,过滤掉大量非候选者,获取较精确的线段反k最近邻查询候选集合。将Voronoi图和本文提出的网络线段Voronoi图的基本性质相结合,给出定理1和定理2,为过滤线段反k最近邻的查询算法提供了基础理论支持。 定理1线段li为网络线段Voronoi图中NLVP(li)的生成线段,那么lq的第一个反向最近邻为li,且对于NLVP(li)中的查询线段的下一个最近邻一定在与NLVP(li)邻接的NLVP中。 Fig.1 Example of theorem 1 and theorem 2图1 基于定理1和定理2的示例图 证明该定理可用反证法证明。如图1(左上角)所示,对于查询线段lq,设其左右端点分别为a和b。对于线段l8,设其左右端点分别为x和y。对于线段l7,设其左右端点分别为q和p。b23和b24为NLVP(l1)和NLVP(l8)之间的边界点。b31为NLVP(l7)与NLVP(l8)之间的边界点。由于lq在NLVP(l1)中,从而对于查询线段lq的1-LRNN为l1。假设lq的2-LRNN存在于与NLVP(l2)不相邻的NLVP中,即为l7。根据点到线段的距离定义,求b24到lq的距离,过点b24做线段lq的垂线交于点o,则b24到lq的距离表示为d(b24,o)。由于点b31到线段l7的垂足不在l7上,从而点b31到线段l7的距离为d(b31,p)。同理点b24到线段l8的距离为d(b24,x),点b31到线段l8的距离为d(b31,x)。根据网络线段Voronoi图的性质,可计算出查询线段lq到线段l7的最短路径d(lq,l7),即为d(lq,l7)=d(b24,o)+d(b24,b31)+d(b31,p)。同理,lq到l8的最短距离d(lq,l8)=d(b24,x)+d(b24,o)。由网络线段Voronoi图的性质可知d(b31,p)=d(b31,x)。由于在路网中满足三角不等式定理,可以得到不等式d(b31,x)+d(b24,b31)>d(b24,x),即d(b24,o)+d(b24,b31)+d(b31,p)>d(b24,x)+d(b24,o),从而得到d(lq,l7)>d(lq,l8)。与假设lq的下一个最近邻在与NLVP(l2)不相邻的NLVP中相矛盾,故原性质成立。 □ 定理2在网络线段Voronoi图中,存在邻接生成线段li和lj,它们之间的距离记为d(li,lj),假设查询线段的最近邻为li,如果有d(lq,li)>d(li,lj),则li、lj被剪枝。 证明该定理可用反证法证明。如图1(右下角)所示,设定线段l4为查询线段,其左右端点分别为h和s。线段l15是查询线段l4的最近邻,其左右端点分别为m和n,两线段之间的最短距离用d(l4,l15)表示。同理证明定理1中的距离计算方法d(l4,l15)=d(s,b14)+d(b14,m)。存在与线段l15邻接的线段l16,其左右端点分别为w和v。线段l15与线段l16之间的距离可以表示为d(l15,l16)=d(v,b32)+d(b32,m)。假设d(l4,l15) 本小节提出的过滤算法的主要思想为:首先通过定理1提供的理论,判断查询线段的位置,如果lq在NLVP(li)中,则线段li为lq的第一个反向最近邻,将li插入到候选集中,并对li的邻接生成线段继续判断,过滤掉大量非候选者。然后根据定理2,对LC中的候选线段进一步判断,将满足条件的线段进行剪枝,有效地提高了查询算法的效率。 基于以上讨论,进一步给出过滤算法,如算法2所示。 算法2RVLRkNN_Filter(L,lq,k) 输入:数据线段集L,查询线段lq,k值 输出:过滤后的候选集LC Begin 1.Create_NLVD(L∪lq);/*创建网络线段Voronoi图*/ 2.LC←∅;/*初始化候选集为空*/ 3.fori=1 tokdo 4.iflq∈NLVP(li)then 5.LC←li;/*将lq的第一个反向最近邻加入到LC中*/ 6.end if 7.elsei++ 8.iflx与lq是邻接的then 9.LC←li+lx; 10. elselx被过滤掉 11.end if 12.ifly是lq的最近邻andd(lq,ly)>d(lx,ly)then 13.LC←LC-lx-ly; 14.end if 15.end for 16.returnLC; End RVLRkNN_Filter算法的具体过程为:首先以数据线段集L和查询线段lq的并集为生成线段创建网络线段Voronoi图。然后根据定理1,对数据线段进行过滤。根据定理2,对得到的候选结果做进一步筛选,满足条件的线段被剪枝,最后剩下为排除掉非候选者的结果集合。如图1所示,lq存在于NLVP(l1)中,因此其1-LRNN为线段l1,它的2-LRNN一定存在于候选集{l2,l3,l9,l8}中。再根据定理2进一步判断,线段l3和l9满足条件,因此被剪枝,得出候选集合为{l2,l8}。 3.1.2 精炼过程 本小节提出的精炼算法主要以过滤过程中所得到的候选集LC为对象进行操作。首先计算查询线段到新加入到候选集合中的生成线段的最短距离,然后对所得到的最短距离进行比较,从而得到更精确的线段反k最近邻的查询结果。 为了计算查询线段到新生成的线段的最短距离,进一步给出定理3、定理4和定理5。 定理3在网络线段Voronoi图中,假设查询线段lq的前两个反向最近邻为{li,lj},那么NLVP(li)与NLVP(lj)一定是相邻的,即NLVP(li)与NLVP(lj)之间存在公共边。 证明此定理可以使用反证法证明。如果查询线段lq到lj的最短路径经过NLVP(lk),并且lk不属于{li,lj},lj是紧挨着li的邻接生成线段,那么查询线段lq到lk在NLVP(lk)中所经过的最短路径要比到线段lj的距离近。如图2所示,假设{l2,l3}是查询线段lq的前两个反向最近邻,令从lq到l3的最短路径为L={p,n1,n4,b3,b6,e},它与NLVP(l4)相交于边界点b3、b6。令从查询线段lq到l4的路径为L′={p,n1,n4,b3,s}。连接点s和b6,根据网络线段Voronoi图的性质可得d(s,b6)=d(e,b6)。已知在路网中满足三角不等式定理,即存在不等式d(s,b6)+d(b3,b6)>d(b3,s),从而可得不等式d(b3,b6)+d(b6,e)>d(b3,s),即L>L′。因此线段l4比线段l3更接近lq。这与假设矛盾,故原定理成立。 □ Fig.2 Example of theorem 3图2 基于定理3的示例图 定理4在网络线段Voronoi图中,假设 {l1,l2,…,lk}为查询线段lq的前k个反向最近邻,那么NLVP(l1),NLVP(l2),…,NLVP(lk)一定是相邻的,即NLVP(l1), NLVP(l2),…,NLVP(lk)互相之间存在公共边。 证明此定理是定理3的一般化,同理依然可以采用反证法进行证明。假设查询线段lq到lk的最短路径通过NLVP(li),并且li∉{l1,l2,…,lk},那么在NLVP(li)中的最短路径比lk更接近li。这与假设{l1,l2,…,lk}为查询线段lq的前k级邻接生成线段相矛盾,故原定理成立。 □ 定理5在网络线段Voronoi图中,对于NLVP(li)的生成线段li,li到其n级邻接生成线段的最短距离小于到NLVP(li)的任意n+1级邻接生成线段的距离。 证明由定理1可知,对于生成线段li而言,NLVP(li)内任何一个查询线段的下一个反向最近邻一定是在与NLVP(li)相邻的NLVP中。由网络线段Voronoi图的性质可知,li到其所有n+1级邻接生成线段必经过NLVP(li)的所有n级邻接生成线段。故li到其n级邻接生成线段的最短距离小于到NLVP(li)任意n+1级邻接生成线段的距离。 □ 基于定理3、定理4、定理5,本小节提出的精炼算法主要思想为:首先初始化查询结果集,调用过滤过程算法,得到候选集LC。然后利用点到线段的距离定义计算最短距离,并对候选集作进一步筛选,得到最终查询结果。 基于以上讨论,进一步给出精炼算法,如算法3所示。 算法3STA_RVLRkNN(L,lq,k) 输入:数据线段集L,查询线段lq,k值 输出:线段反k最近邻查询结果集LR Begin 1.LR←∅;/*初始化查询结果集为空*/ 2.dist(li,lj)←∅;/*初始化最短路径为空*/ 3.LC←RVLRkNN_Filter(L,lq,k); 4.while(LC!=NULL)do 5.设l的两端点分别为s、e; 6.过边界点bi做线段li垂直平分线垂足为o; 7.ifo∈li 8.dist(li,bi)=dist(bi,o); 9.elseo∉li 10.dist(li,bi)=min{dist(bi,s),dist(bi,e)}; 11.end if 12.iflx与ly是相邻的andlx,ly∈LCthen 13.dist(lx,lq)=dist(lx,bz)+dist(bz,lq);/*其中bz为NLVP(lx)与NLVP(lq)之间的边界点*/ 14.dist(ly,lq)=dist(ly,bs)+dist(bs,lq);/*其中bs为NLVP(lx)与NLVP(lq)之间的边界点*/ 15.end if 16.compare min{dist(lx,lq)};/*比较出lx与lq之间的最小距离*/ 17.ifdist(ly,lq)>dist(bs,lq)then 18.LC←LC-ly;/*从候选集中将ly删除*/ 19.else 20.LR←LC+lx;/*将线段lx添加到结果集中*/ 21.end if 22.end while 23.returnLR End STA_RVLRkNN算法的具体过程为:首先初始化查询结果集并调用算法2,得到候选集LC。根据定理3,最短路径由两部分组成,一部分为查询线段到边界点的距离,另一部分为生成线段到边界点的距离。设线段li的左右端点分别为是s和e,过边界点bi做线段li的垂直平分线,垂足为o。如果o在线段li上,则dist(li,bi)=dist(bi,o),如果o不在线段li上,则dist(li,bi)=min{dist(bi,s),dist(bi,e)}。从而得到lq到已经计算出的k个LRNN所在的NLVP共同边的最短距离,最后得到精确的查询结果集。 3.2 数据线段集合变化对查询结果的影响 数据线段集L的变化对查询结果会产生一定的影响,主要分为两部分,即新增数据线段对查询结果的影响,以及移除数据线段对查询结果的影响。 3.2.1 新增数据线段对查询结果的影响 在现实社会中,空间数据集中的线段对象的数量是不稳定的。当数据线段集新增线段时,有可能会对原有的查询结果产生影响,因此本小节主要讨论向查询线段集增加数据线段时的解决方法,并提出算法DYN_ADD_RVLRkNN。根据数据线段动态增加的情况给出实例,如图3所示。以lq的前两个最近邻为例,给定数据线段集L={l1,l2,…,l26},查询线段为lq,新增线段为l′。以s为圆心,经计算假设l3到lq的距离最短,则以lq到l3的距离d(lq,l3)为半径,绘制圆S,根据本文前面提到的计算方法可得d(lq,l3)=d(lq,s)。 Fig.3 Example of adding line图3 新增线段示例图 根据新插入的线段所在的位置,来决定是否重新进行线段反k最近邻查询。新增数据线段对查询结果的影响可分为两种情况:新增数据线段不在圆S中,则对查询结果集合没有影响,直接返回上次的查询结果集合即可。新增数据线段在圆S内,则对查询结果集合有影响,需将新增数据线段加入到数据线段集L中,重新计算查询结果集合。结合图2,在没有加入新增线段的情况下,针对lq的前两个反向最近邻进行说明,lq的1-LRNN为l2,它的2-LRNN存在于候选集{l1,l4,l6}中,经过计算假设l1到lq的距离更近,则它的2-LRNN为{l1,l2}。如图3所示,假设新增线段为l′,它包含于圆S中,因此对查询结果有影响,将其插入到L中,得到新的线段集L′={l′,l1,l2,…,l26},重新查询得线段lq的第一个反向最近邻为l′,经过计算假设l3到lq的距离更近,则它的2-LRNN为{l′,l3}。 基于以上讨论,给出算法4。 算法4DYN_ADD_RVLRkNN(L,lq,l′,k) 输入:数据线段集L,查询线段lq,新插入线段l′,k值输出:新增数据线段后线段反k最近邻的查询结果 Begin 1.Lnew←∅;/*初始化查询结果为空集*/ 2.LR←∅;/*初始化候选集为空集*/ 3.Dist(d)←∅;/*初始化线段间最短距离为空集*/ 4.L′←L+l′;/*将新增线段l′加入到数据线段集合L中*/ 5.call STA_RVLRkNN(L,lq,k);/*得到候选集LR*/ 6.d(li,lq)=d(li,bz)+d(bz,lj);/*计算线段li与lq之间的距离,其中bz为边界点*/ 7.Dist(d)←d(li,lq); 8.CR←Circle(s,d(s,lq));/*以点s为圆心,d(s,lq)为半径构造圆S*/ 9.Judge_Postion(l′);/*判断新插入线段的位置*/ 10.ifl′∈CRthen 11.returnSTA_RVLRkNN(L′,lq,k); 12.Lnew←LR; 13.end if 14.ifl′∉CRthen 15.Lnew←LR; 16.end if 17.returnLnew; End 算法DYN_ADD_RVLRkNN首先初始化集合Lnew,LR和Dist(d)为空。将新增线段l′添加到数据线段集L中,得到新的数据线段集L′。接着调用STA_RVLRkNN算法,计算出线段li与查询线段lq之间的距离,并添加到Dist(d)集合中。然后以点s为圆心,d(s,lq)为半径构造圆S,若新增线段l′在圆S内,则对查询结果有影响,重新调用STA_RVLRkNN算法并根据新的数据线段集L′重新进行计算;若l′不在圆S中,则新增线段对原查询结果没有影响,直接返回原查询结果即可。 3.2.2 移除数据线段对查询结果的影响 在大多情况下,空间数据集的动态变化是不确定的。如果将某数据线段从数据线段集中移除,有可能对原有的查询结果产生影响。下面讨论从数据线段集中移除线段对查询结果的影响,并提出算法DYN_DEL_RVLRkNN。 根据移除数据线段是否在查询结果中,对查询结果的影响可以分为两种情况:一种情况为所移除的数据线段不在查询结果集合中,则它对查询结果没有影响,直接返回上次的查询结果集合即可。另一种情况为所移除的数据线段在查询结果集合中,则从数据线段集L中撤除该数据线段,并重新计算查询结果。如图3所示,针对lq的前两个反向最近邻来说,假设移除线段l2,由于l2不属于查询结构集,从而查询结果不变。假设移除线段为l′,在移除之前,由于l′包含在查询结构集中,此时lq的第一个反向最近邻存在于候选集{l1,l3,l5}中。经计算l1到lq的距离更近,则它的1-LRNN为l1,可以根据查询算法再继续查找它的2-LRNN,显然最终的查询结果发生了改变。 基于以上讨论,给出算法5。 算法5DYN_DEL_RVLRkNN(L,lq,l′,k) 输入:数据线段集L,查询线段lq,移除线段l′,k值 输出:移除数据线段后线段反k最近邻的查询结果 Begin 1.Lnew←∅;/*初始化查询结果为空集*/ 2.LR←∅;/*初始化候选集为空集*/ 3.Dist(d)←∅;/*初始化线段最短距离为空集*/ 4.L′←L-l′;/*从数据线段集合L中移除l′*/ 5.call STA_RVLRkNN(L,lq,k);/*得到候选集LR*/ 6.ifl′∈LRthen 7.retrun STA_RVLRkNN(L′,lq,k); 8.Lnew←LR; 9.end if 10.ifl′∉LRthen 11.Lnew←LR; 12.end if 13.returnLnew; End 算法DYN_DEL_RVLRkNN首先初始化集合Lnew,LR和Dist(d)为空,将待移除线段l′从数据线段集L中移除,得到新的数据线段集L′。然后调用STA_RVLRkNN算法,得到数据线段集为L′时的查询结果。进一步对结果集进行判断,分为两种情况:若结果集包含l′,则移除该线段会对查询结果产生影响,需对L′重新调用STA_RVLRkNN算法,得到新的结果集合Lnew;如果结果集合不包含l′,则可以判断移除该线段对查询结果没有影响,直接将原结果集合赋给新结果集合即可。 本文首次提出了路网中线段反k最近邻查询问题,并给出了查询方法。但现有的路网反k最近邻查询都是以空间点为基础的,不能用于路网环境下线段反k最近邻查询问题,因此无法直接与本文算法进行比较。为了得到比较算法,设计了一个较为基础的算法RNLRkNN_Basic。RNLRkNN_Basic算法是对文献[18]中提出的线段最近邻(line nearest neighbor,LNN)查询算法的反复运用,其主要思想为:在路网环境下反复调用LNN算法,将其应用于线段反k最近邻查询中。首先对线段集中的一个线段反复调用LNN算法,得到相应的查询结果LkNN。然后对该线段的LkNN进行判断,如果查询结果中存在查询线段,则将该线段添加到查询结果集中。如果查询结果中不包含该线段,则继续调用LNN算法并进行判断,最后得到LRkNN查询结果。 本实验的运行环境为:2.0 GHz CPU,4 GB内存,500 GB硬盘,Windows 7系统。实验采用的路网数据集是美国旧金山和加州的路网信息(http://konect.unikoblenz.de/networks/roadNet-CA)。实验中,对目标线段和分布进行了适度调整。集合Q中的查询线段均匀分布在路网的子区域中。用A表示子区域占整个路网的百分比;用参数F表示边的权值与实际长度的偏离程度,F=权值/欧氏距离。在默认情况下,分布在A=5%的路网图中,目标线段的密度P=0.05,参数F=2。对于每次实验,实验结果均为执行20次的平均值。 对静态数据情况下的RVLRkNN查询算法(STA_ RVLRkNN)进行测试。首先测试k值、数据集大小、目标线段密度P对CPU时间的影响。其次测试k值和数据集大小对两算法I/O代价的影响。进一步测试动态数据集情况下两查询的性能。最后对两算法的准确率进行测试。 Fig.4 Effect ofkon CPU query time图4 k值对CPU时间的影响 首先,测试k值变化对CPU时间的影响,实验结果如图4所示。从图4中可以看出,随着k值的不断变大,两算法的CPU时间均呈上升趋势。其中RNLRkNN_Basic算法的CPU上升趋势在k值达到一定程度时增长显著,STA_RVLRkNN算法上升趋势比较平缓。由于RNLRkNN_Basic算法需要对线段集中的每个线段计算它的LkNN,随着k值的增加,造成了搜索区域大量重叠的情况,查询所用的时间较长。而本文提出的路网中基于Voronoi图的STA_ RVLRkNN算法在预处理阶段排除掉大量非候选者,有效地缩小了查询范围,因此查询所用的时间比RNLRkNN_Basic算法少。 其次,在其他条件不变的情况下,k=15,测试在不同大小的数据集环境下对算法CPU时间的影响,实验结果如图5所示。从图5中可以看出,随着数据集的增大,两算法的CPU时间均呈上升趋势。但本文提出的STA_RVLRkNN算法的上升趋势较为平缓,而RNLRkNN_Basic算法的变化趋势在数据集规模达到一定程度时上升比较迅速。这是由于STA_ RVLRkNN算法有效地利用了过滤过程,缩小了查询范围,从而降低了查询时间。对于RNLRkNN_Basic来说,则要对数据集中的每一个线段搜索它的LkNN,浪费了大量时间。故在其他条件相同时,只考虑对CPU时间的影响,STA_RVLRkNN算法较优。 Fig.5 Effect of data set size on CPU query time图5 数据集规模对CPU时间的影响 进一步分析目标线段密度对CPU时间的影响,在k=15,目标线段密度不同的情况下分别对两算法进行测试,实验结果如图6所示。从图6中可以看出,两算法的CPU时间均随密度P值的增大而增多。这是因为随着P值的增大意味着目标线数量变多,STA_ RVLRkNN算法在计算候选线段时,需要访问更多的NLVP,因此造成CPU时间的增大。同理RNLRkNN_Basic算法需要通过计算更多的线段间距离从而判断LkNN。当目标线段较稠密时,STA_RVLRkNN算法CPU时间增长较快。但在实际生活中,目标线段的密度通常远小于0.08。 Fig.6 Effect ofPon CPU query time图6 目标线段密度对CPU时间的影响 在其他条件一定时,针对k值的变化对算法I/O代价的影响进行测试。根据实验测试数据绘制条形图,如图7所示。RNLRkNN_Basic算法的I/O代价随着k值的增长,上升趋势比较显著,而STA_RVLRkNN算法相对来说I/O代价上升趋势较为平缓。这是因为RNLRkNN_Basic算法需要计算每一条线段的LkNN,随着k值的增加,算法在查询过程中所要存储和访问的线段也逐渐增多,从而造成该算法的I/O代价较高。对于STA_RVLRkNN算法,在过滤过程中排除掉大量非候选者,因此降低了查询算法的I/O代价。故在其他条件相同时,只考虑对I/O代价的影响,STA_RVLRkNN算法性能更优。 Fig.7 Effect ofkon I/O cost图7 k值对I/O代价的影响 进一步测试数据规模对I/O代价的影响,实验结果如图8所示。算法RNLRkNN_Basic的I/O代价随着数据集的增长,变化趋势较为明显,STA_RVLRkNN算法的变化趋势较为缓慢。这是因为RNLRkNN_ Basic算法中需要计算每一个线段的LkNN,由于数据集中线段越多,造成查询过程中的无关数据访问量越多,从而导致I/O代价不断变大。而STA_ RVLRkNN算法在过滤阶段排除了大量非候选者,减少了对无关数据的访问,故而I/O代价较小,且随着数据集规模的增加I/O代价增长缓慢。因此在其他条件相同时,只考虑对I/O代价的影响,STA_RVLRkNN算法更优。 Fig.8 Effect of data set Size on I/O cost图8 数据集规模对I/O代价的影响 针对动态数据集情况下的LRkNN查询算法的性能进行测试。在路网环境下将重复调用RNLRkNN_ Basic算法的方式应用于动态数据集情况中,形成对比算法。当线段动态增加时,该算法的主要思想为:将新的线段添加到数据集中形成新的数据线段集,重新调用原有的算法,从而得出结果集。当线段动态减少时,该算法的主要思想为:将某一线段从线段集中移除形成新的数据线段集,重新调用原有的算法得出结果集。 设定线段数量为8 000,k=15,在路网环境下分别运行DYN_ADD_RVLRkNN算法和RNLRkNN_Basic算法,得到其CPU运行时间记录到表1中。在其他环境不变时,线段以每次增加一条的方式进行测试,重复运行并取时间的平均值,记录其时间到表1中。从表1中可以看出,当数据线段动态增加时DYN_ADD_RVLRkNN算法的CPU时间有所增加,但变化不明显。而RNLRkNN_Basic算法的CPU时间变化相对增长幅度较大。这是因为当增加一条线段时DYN_ADD_RVLRkNN算法会先判断其是否在影响区域内,然后采取不同的策略。而RNLRkNN_Basic算法则要重新执行一遍算法。因此,在数据集增加线段的情况下,只考虑对CPU时间影响的因素,DYN_ADD_RVLRkNN算法的性能优于RNLRkNN_ Basic算法。 Table 1 Performance comparison between DYN_ADD_RVLRkNN and RNLRkNN_Basic表1DYN_ADD_RVLRkNN与RNLRkNN_Basic算法性能比较 进一步在线段动态减少的情况下进行测试,分别运行DYN_DEL_RVLRkNN算法和RNLRkNN_Basic算法,得到CPU时间并记录到表2中。然后,保证其他条件不变,每次减少一条线段并记录其CPU时间,重复运行算法,计算其平均时间并记录到表2中。从时间的变化可以看出,虽然算法的时间都有增长,但DYN_DEL_RVLRkNN算法增长的幅度远小于RNLRkNN_Basic算法。这是由于DYN_DEL_RVLRkNN算法会对删除的线段进行判断,然后再采取相应的策略。而RNLRkNN_Basic算法需要对新的数据集重新运行一次,形成了较多的冗余数据,比较浪费查询时间。因此在数据集减少线段的情况下,只考虑对CPU时间影响的因素,DYN_DEL_RVLRkNN算法的性能优于RNLRkNN_Basic算法。 Table 2 Performance comparison between DYN_DEL_RVLRkNN and RNLRkNN_Basic表2DYN_DEL_RVLRkNN与RNLRkNN_Basic算法性能比较 最后对算法的准确率进行测试。在其他条件不变的情况下数据量为5 000,分别测试静态数据集和动态数据集下两算法的准确率20次,最终结果取其平均值。首先测试准确率随k值的变化情况,如图9所示。从图9中可以看出,随着k值的增加,两算法的准确率存在上升、不变以及减少的情况。这说明准确率与k值之间没有必然的线性关系。设定k=12,测试随着查询次数的增加准确率的变化情况,如图10所示。从图10中可以看出,两算法的准确率均随着查询次数的增加而增加,但本文提出的RVLRkNN算法比RNLRkNN_Basic算法更快速地达到较高的准确率。 Fig.9 Effect ofkon accuracy图9 k值对准确率的影响 Fig.10 Effect of queries number on accuracy图10 查询次数对准确率的影响 本文提出了路网环境下线段反k最近邻查询方法,有效减少了现实生活中对象(例如河流、大型建筑、轨道等)抽象为点时反k最近邻查询所带来的误差,解决了针对静态数据集情况下以及动态数据集情况下的线段反k最近邻查询问题。通过理论研究和实验表明,对于数据集比较稠密的情况本文算法存在着一定的局限性,但在数据集密度较低时,本文算法具有较好的性能。未来的研究重点主要集中在路网环境下的线段最近邻查询。 [1]Gong Caixia,Chen Xinjun,Gao Feng,et al.Development and application of geographic information system in marine fisheries[J].Journal of Shanghai Ocean University,2011,15 (2):134-143. [2]Mookiah M R K,Acharya U R,Koh J E W,et al.Decision support system for age-related macular degeneration using discrete wavelet transform[J].Medical&Biological Engineering&Computing,2014,52(9):781-796. [3]Hong Zixuan,Bian Fuling.Time-space and cognition-space transformations for transportation network analysis based on multidimensional scaling and self-organizing map[C]// SPIE 7144:Proceedings of the Geoinformatics 2008 and Joint Conference on GIS and Built Environment:The Built Environment and its Dynamics,Guangzhou,China,Jun 28-29,2008. [4]Dasarathy B V.Nearest neighbor(NN)norms:NN pattern classification techniques[M].Los Alamitos,USA:IEEE Computer Society Press,1990:217-224. [5]Li Song,Zhang Liping,Hao Zhongxiao.Strong neighbor pair query in dynamic dataset[J].Journal of Computer Research and Development,2015,52(3):749-759. [6]Boiman O,Shechtman E,Irani M.In defense of nearest-neighbor based image classification[C]//Proceedings of the 2008 IEEE Conference on Computer Vision and Pattern Recognition,Anchorage,USA,Jun 23-28,2008.Piscataway,USA: IEEE,2008:1192-1999. [7]Cheng R,Chen Lei,Chen Jinchuan,et al.Evaluating probability thresholdk-nearest-neighbor queries over uncertain data[C]//Proceedings of the 12th International Conference on Extending Database Technology:Advances in Database Technology,Saint Petersburg,Russia,Mar 24-26,2009.New York:ACM,2009:672-683. [8]Zhang Zhaoxing,Fan Xingqi,Zhao Suyun,et al.Fast reduction algorithm research based onk-nearest neighbor fuzzy rough set[J].Journal of Frontiers of Computer Science and Technology,2015,9(1):14-23. [9]Yi Xun,Paulet R,Bertino E,et al.Practical approximateknearest neighbor queries with location and query privacy[J]. IEEE Transactions on Knowledge and Data Engineering, 2016,28(6):1546-1559. [10]Wang Li,Qin Xiaolin,Shi Changyue.Bichromatic reverse nearest neighbor queries in indoor space[J].Journal of Frontiers of Computer Science and Technology,2015,9(3):310-320. [11]Lin Huaizhong,Chen Fangshu,Gao Yunjun,et al.Finding optimal region for bichromatic reverse nearest neighbor in two-and three-dimensional spaces[J].Geoinformatica,2016, 20(3):351-384. [12]Tran Q T,Taniar D,Safar M.Bichromatic reverse nearestneighbor search in mobile systems[J].IEEE Systems Journal,2014,4(2):230-242. [13]Lee K W,Choi D W,Chung C W.DART:an efficient method for direction-aware bichromatic reverseknearest neighbor queries[C]//LNCS 8098:Proceedings of the 13th International Conference on Advances in Spatial and Temporal Databases,Munich,Germany,Aug 21-23,2013.Berlin,Heidelberg:Springer,2013:295-311. [14]Emrich T,Kriegel H P,Ger P,et al.Reversek-nearest neighbor monitoring on mobile objects[C]//Proceedings of the 18th SIGSPATIAL International Conference on Advances in Geographic Information Systems,San Jose,USA,Nov 2-5,2010.New York:ACM,2010:494-497. [15]Lu Bingliang,Cui Xiaoyu,Liu Na.Bichromatic reverse nearestkneighbor query processing on road network[J].Journal of Chinese Computer Systems,2015,36(2):266-270. [16]Yu Xiaonan.A method for reversek-nearest-neighbor queries in obstructed spaces[J].Chinese Journal of Computers, 2011,34(10):1917-1925. [17]Zhu Huaijie,Wang Jiaying,Wang Bin,et al.Location privacy pressing obstructed nearest neighbor queries[J].Journal of Computer Research and Development,2014,51(1):115-125. [18]Hao Zhongxiao,Wang Yudong,He Yunbin.Line segment nearest neighbor query of spatial database[J].Journal of Computer Research and Development,2008,45(9):1539-1545. [19]Gu Yu,Zhang Hui,Wang Zhigang,et al.Efficient movingknearest neighbor queries over line segment objects[J].World Wide Web Internet and Web Information Systems, 2015,19(4):653-677. [20]Liu Runtao,Hao Zhongxiao.Fast algorithm of nearest neighbor query for line segments of spatial database[J].Journal of Computer Research and Development,2011,48(12):2379-2384. [21]Papadopoulou E,Zavershynskyi M.The higher-order Voronoi diagram of line segments[J].Algorithmica,2014,74 (1):1-25. 附中文参考文献: [1]龚彩霞,陈新军,高峰,等.地理信息系统在海洋渔业中的应用现状及前景分析[J].上海海洋大学学报,2011,20(6): 902-909. [5]李松,张丽平,郝忠孝.动态数据集环境下的强邻近对查询[J].计算机研究与发展,2015,52(3):749-759. [8]张照星,范星奇,赵素云,等.k-近邻模糊粗糙集的快速约简算法研究[J].计算机科学与探索,2015,9(1):14-23. [10]王丽,秦小麟,施常月.室内双色数据集上的反向最近邻查询[J].计算机科学与探索,2015,9(3):310-320. [15]卢秉亮,崔晓玉,刘娜.路网中双色反向k近邻查询处理[J].小型微型计算机系统,2015,36(2):266-270. [16]于晓南.一种障碍空间中的反k最近邻查询研究[J].计算机学报,2011,34(10):1917-1925. [17]朱怀杰,王佳英,王斌,等.障碍空间中保持位置隐私的最近邻查询方法[J].计算机研究与发展,2014,51(1):115-125. [18]郝忠孝,王玉东,何云斌.空间数据库平面线段最近邻查询问题研究[J].计算机研究与发展,2008,45(9):1539-1545. [20]刘润涛,郝忠孝.空间数据库平面线段快速最近邻查询算法[J].计算机研究与发展,2011,48(12):2379-2384. 张丽平(1976—),女,辽宁铁岭人,硕士,哈尔滨理工大学副教授、研究生导师,CCF会员,主要研究领域为数据库理论及应用,数据挖掘,数据查询。 GUO Yingying was born in 1993.She is an M.S.candidate at Harbin University of Science and Technology.Her research interests include data mining and data query. 郭莹莹(1993—),女,黑龙江大庆人,哈尔滨理工大学硕士研究生,主要研究领域为数据挖掘,数据查询。 LI Song was born in 1977.He received the Ph.D.degree from Harbin University of Science and Technology.Now he is an associate professor at Harbin University of Science and Technology,and the member of CCF.His research interests include database theory and application,data mining and data query. 李松(1977—),男,江苏沛县人,博士,哈尔滨理工大学副教授、研究生导师,CCF会员,主要研究领域为数据库理论及应用,数据挖掘,数据查询。 LI Shuang was born in 1991.She is an M.S.candidate at Harbin University of Science and Technology.Her research interests include data mining and data query. 李爽(1991—),女,黑龙江哈尔滨人,哈尔滨理工大学硕士研究生,主要研究领域为数据挖掘,数据查询。 FAN Ruiguang was born in 1993.He is an M.S.candidate at Harbin University of Science and Technology.His research interests include data mining and data query. 樊瑞光(1993—),男,黑龙江哈尔滨人,哈尔滨理工大学硕士研究生,主要研究领域为数据挖掘,数据查询。 Line ReversekNearest Neighbor Query in Road Network* ZHANG Liping+,GUO Yingying,LI Song,LI Shuang,FAN Ruiguang To remedy the defects that existing methods can not deal with the line segment reverseknearest neighbor (RkNN)query in road network,this paper puts forward the line segment RkNN query method in road network.The query method is mainly used to assess the scope of query object.Based on the characteristics of road network and Voronoi diagram,the network line Voronoi diagram(NLVD)concept is proposed.According to the property of NLVD,the STA_RVLRkNN is given in static line segment set environment,the query includes two parts:filtering and refining processes.Further,DYN_RVLRkNN method is given in dynamic line segment set environment,this query is divided into two parts of adding and deleting space segment objects,then the corresponding algorithm is proposed for different situations and new query result set is obtained.The theatrical study and experimental results show that the algorithm can effectively deal with the line segment RkNN query in road network. road network;network line Voronoi diagram(NLVD);reverseknearest neighbor ing was born in 1976.She the M.S.degree from Harbin University of Science and Technology. Now she an associate professor at Harbin University of Science and Technology,and the member of CCF.Her research interests include database theory and application,data mining and data query. A TP311.13 *The Science and Technology Research Project of Heilongjiang Provincial Education Department under Grant No.12531z004(黑龙江省教育厅科学技术研究项目). Received 2016-04,Accepted 2016-09. CNKI网络优先出版:2016-09-08,http://www.cnki.net/kcms/detail/11.5602.TP.20160908.1045.004.html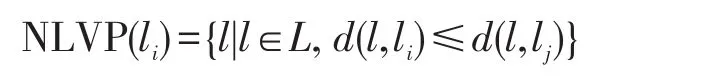
3 路网环境下LRkNN查询

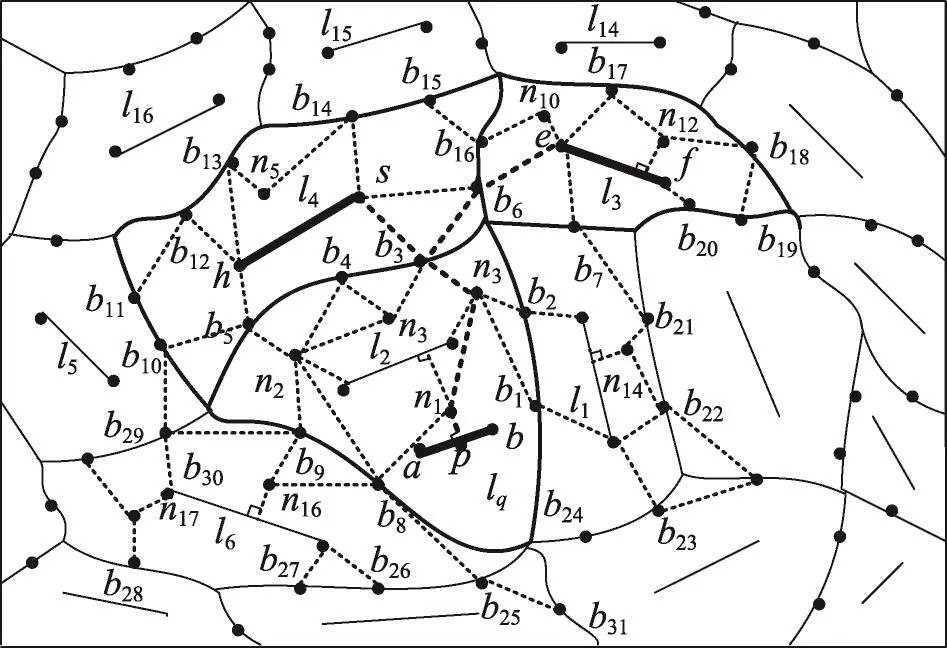

4 实验与分析
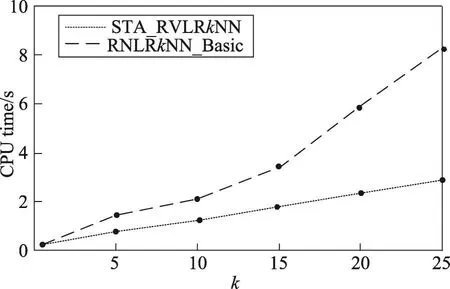
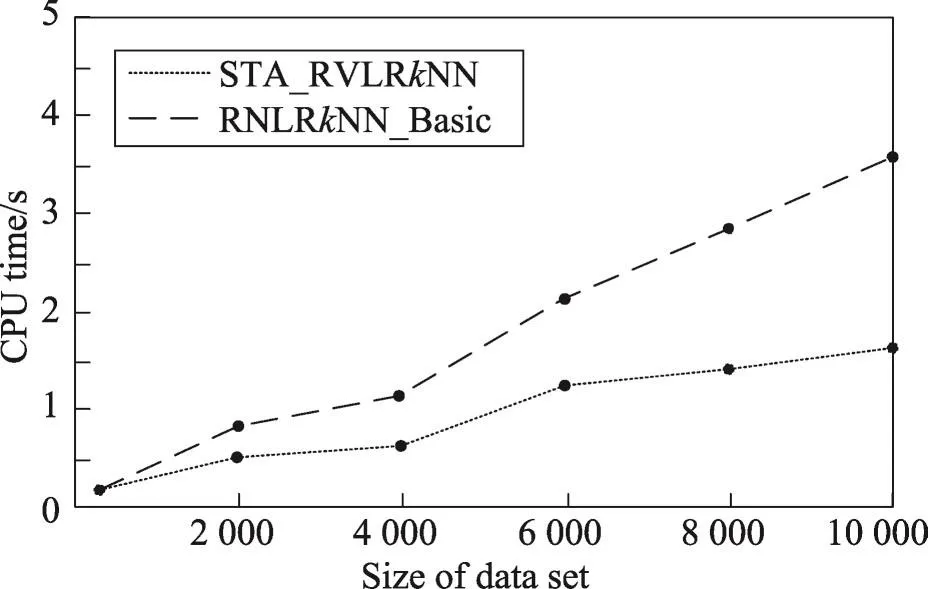



5 结束语





College of Computer Science and Technology,Harbin University of Science and Technology,Harbin 150080,China
+Corresponding author:E-mail:zhanglptg@163.com

