基于Spark的序列数据质量评价*
韩 超,段 磊,2+,邓 松,王慧锋,唐常杰
1.四川大学 计算机学院,成都 610065
2.四川大学 华西公共卫生学院,成都 610041
3.南京邮电大学 先进技术研究院,南京 210003
基于Spark的序列数据质量评价*
韩 超1,段 磊1,2+,邓 松3,王慧锋1,唐常杰1
1.四川大学 计算机学院,成都 610065
2.四川大学 华西公共卫生学院,成都 610041
3.南京邮电大学 先进技术研究院,南京 210003
HAN Chao,DUAN Lei,DENG Song,et al.Evaluation of sequential data quality using Spark.Journal of Frontiers of Computer Science and Technology,2017,11(6):897-907.
随着序列数据在实际中的广泛应用,序列数据质量评价成为学术、工业等众多领域的热门研究问题。目前主流的序列数据质量评价方法是基于概率后缀树模型进行数据质量评价,然而这种方法难以实现对大规模数据的处理。为解决此问题,提出了基于Spark的序列数据质量评价算法STALK(sequential data quality evaluation with Spark),并且采用了改进的剪枝策略来提高算法效率。具体地,在Spark平台下,利用大规模序列数据高效建立生成模型,并根据生成模型对查询序列的数据质量进行快速评价。最后通过真实序列数据集验证了STALK算法的有效性、执行效率和可扩展性。
数据质量;概率后缀树;Spark;并行计算
1 引言
大数据时代下的数据信息成为社会关注焦点。数据质量的高低影响其承载信息的利用效率和传播广度。高质量的数据是统计分析、数据挖掘、决策支持的基石;含有误差、噪声等质量差的数据会降低数据信息的利用和价值,降低生产生活效率。
传统的数据质量评价主要依靠定性策略,即从数据的一致性、完整性、及时性和准确性等指标进行统计分析[1]。针对序列数据,传统质量评价算法缺少对数据模型和序列元素出现周期性变化的分析,对此文献[2]考虑间隔约束,提出通过概率后缀树[3]和马尔科夫链型生成训练模型的数据质量评价方法。然而,文献[2]提出的SQEPST(sequence quality evaluation based on probability suffix tree)算法伸缩性差,难以适用大规模数据。
Spark框架具有较高的容错性和伸缩性[4],为解决大规模序列数据质量评价问题,本文利用Spark框架,考虑概率后缀树和马尔科夫链型[2],提出了基于Spark的序列数据质量评价算法STALK(sequential data quality evaluation with Spark),即根据给定的可靠序列数据集训练序列生成模型,并用其对查询序列进行质量评价。
为实现基于Spark框架的大规模序列数据质量评价,本文在文献[2]工作基础上需要克服以下挑战:(1)针对Spark集群计算的特点,分析选用合适的序列数据生成模型的学习策略对提高算法执行效率至关重要;(2)为提高Spark集群中各计算节点的效率,设计有效的剪枝策略是实现并行建立概率后缀树的关键;(3)设计适合Spark架构的高效数据分发和共享策略是实现对查询序列的快速质量评价的基础。
本文主要贡献有:(1)提出了基于Spark的大规模序列数据质量评价问题;(2)讨论了Spark框架上生成概率后缀树的方法,并设计了基于Spark的序列数据质量评价算法STALK;(3)实验验证了STALK算法的有效性、执行效率和可扩展性。
本文组织结构如下:第2章给出本文研究问题定义;第3章介绍相关工作;第4章讲述基于Spark的序列数据质量评价算法STALK;第5章通过实验验证STALK算法的有效性、执行效率和可扩展性;第6章总结本文工作,并对未来工作进行展望。
2 问题定义
给定序列样本集合D,定义Σ为D中序列元素的集合,|S|为D中序列样本S的长度,S[k]表示序列S中第k(1≤k≤|S|)个元素。为便于表达,定义如下对序列S的操作:
Suf(S)为S的最大后缀,Suf(S)=S[2]S[3]…S[|S|];
Pre(S)为S的最大前缀,Pre(S)=S[1]S[2]…S[|S|-1];
Apd(S,e)表示在S末尾拼接元素e组成的新序列,即Apd(S,e)=S[1]S[2]…S[|S|]e。
给定序列S和S′,若存在正整数k1,k2,…,km满足1≤k1
间隔约束γ是一个正整数域区间,记为γ=[γ.min,γ.max](0≤γ.min≤γ.max)。若序列S′在S上存在一个实例并且满足∀m>1,有km-km-1-1∈γ,那么称S′匹配S,记为S′⊆γS。
例1给定序列S=abbaabaa,当序列S′=abb,间隔约束γ=[0,1],S′在S中的实例集合为{<1,2,3>,<1,2,6>,<1,3,6>},其中存在实例<1,2,3>满足2-1-1∈γ且3-2-1∈γ,因此S′⊆γS。
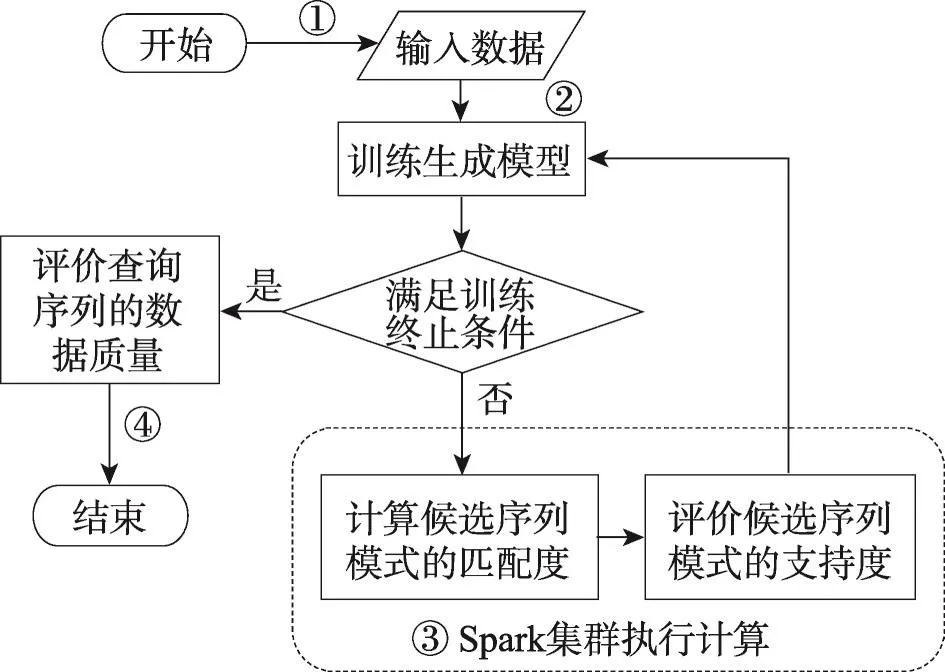
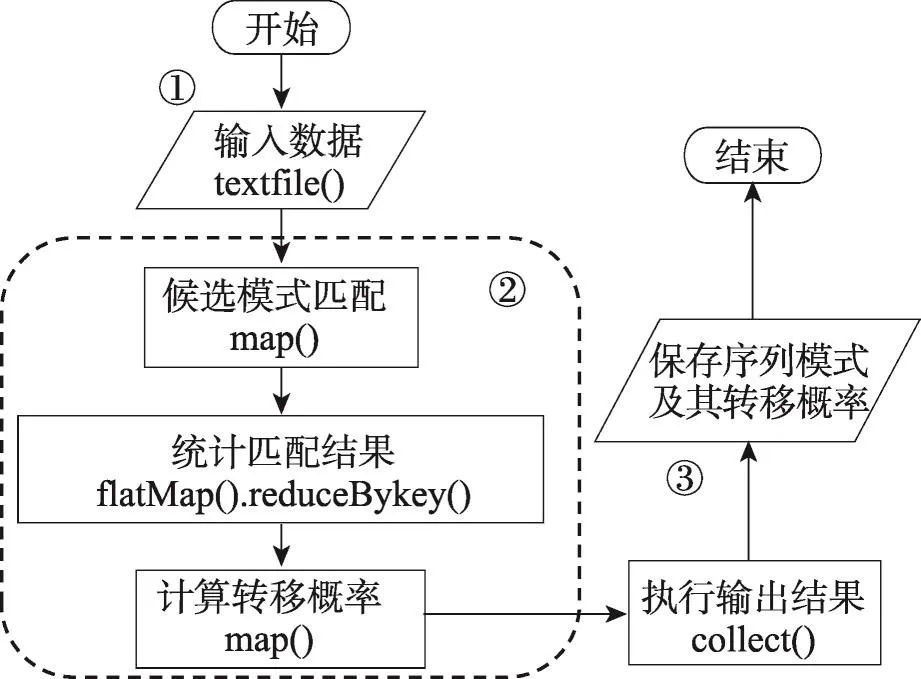
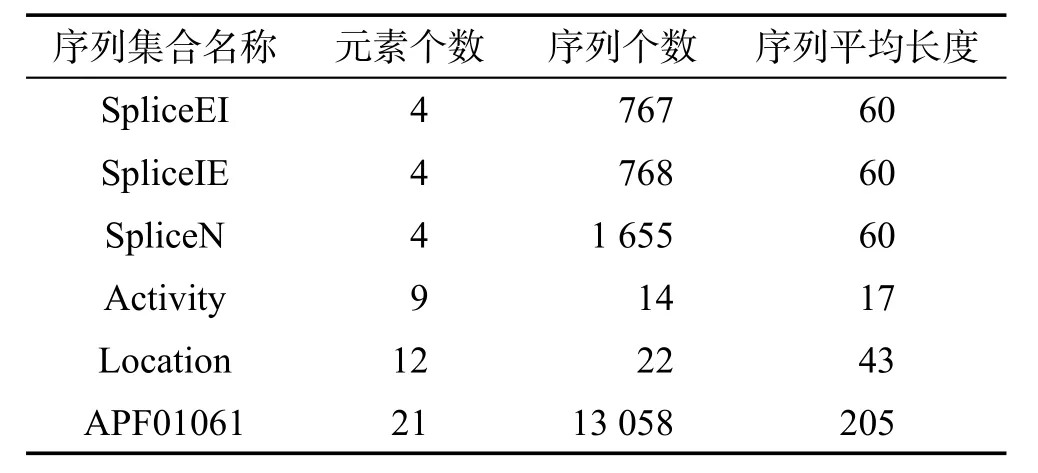
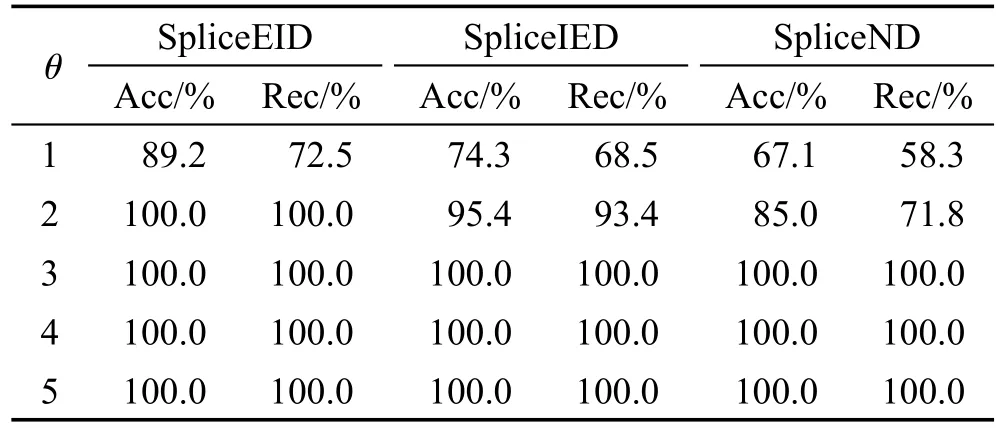
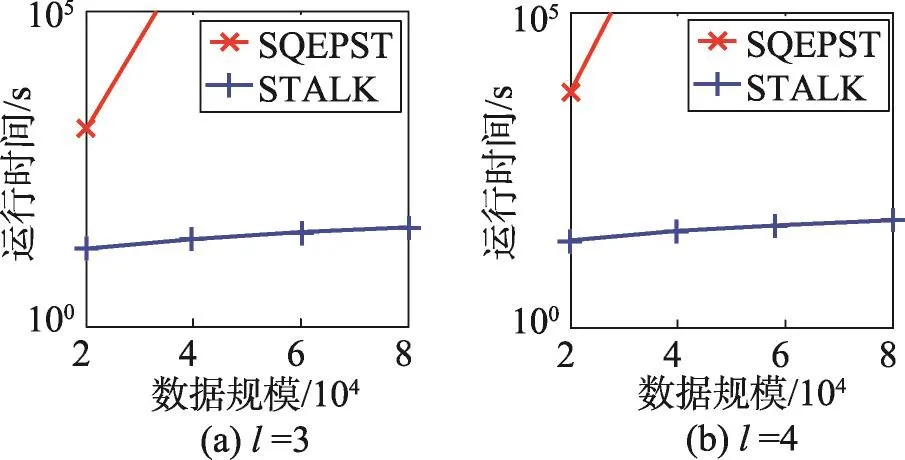
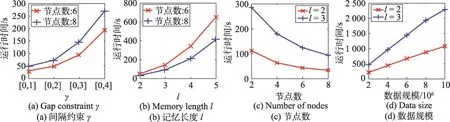
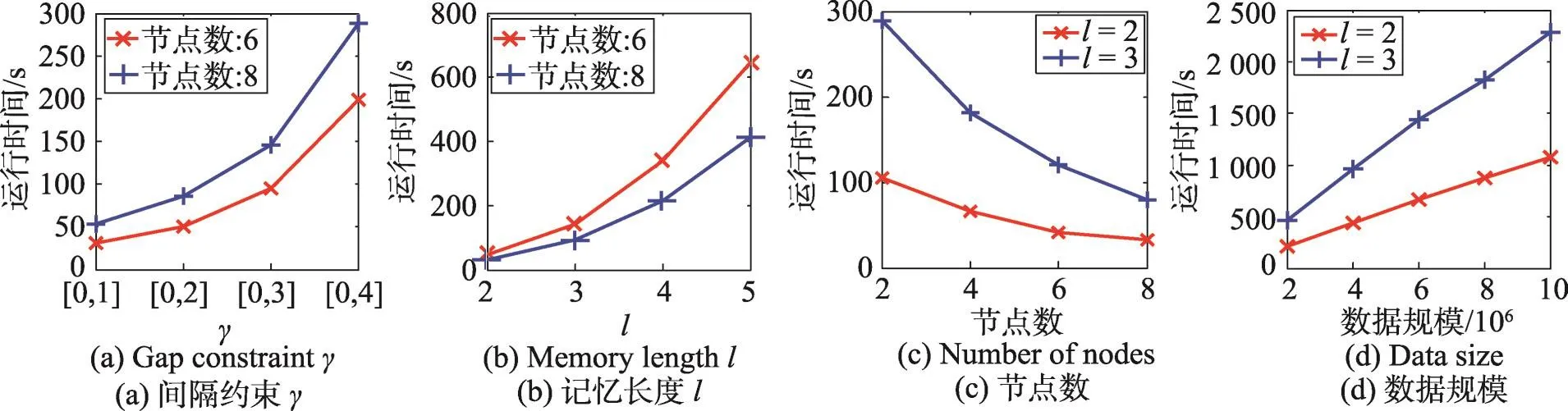
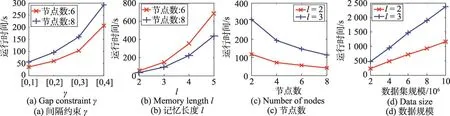
定义1(匹配度)给定序列S′、S,间隔约束γ,S′在S中满足γ-匹配的实例集合称为S′在S中的匹配集合,记为match(S′,S)。match(S′,S)={ 给定序列S′,序列样本集合D,间隔约束γ,称D中与S′满足γ-匹配的序列样本数占总样本数的比例为S′在D的支持度,记为Sup(S′,D,γ),如式(1): 例2考虑表1中的序列样本集合D,令γ=[0,1]。给定序列S′=ab,对序列S1有实例<1,2>、<1,3>、<4,6>、<5,6>、<5,7>使得S′⊆γS1,对序列S2有实例<1,2>、<1,3>、<4,5>、<6,7>使得S′⊆γS2,对序列S3有实例<1,2>、<3,4>、<3,5>使得S′⊆γS3。由于|D|=3,则Sup(S′,D,γ)=(1+1+1)/3=1.0。 Table 1 An example of a set of sequences表1 序列集合示例 定理1给定间隔约束γ,序列样本集合D,序列模式S′和S,其中S′为S的连续子序列,那么Sup( 证明由于S′为S的连续子序列,那么给定样本集合D,间隔约束γ,对于任意序列P(P∈D),S′⊆γP成立,但S⊆γP不一定成立,则|match(S′,P)|≥|match(S,P)|,根据式(1)可得: 假设序列样本集合D中所有序列的生成服从分布Ẑ。对于查询序列S,用L(S|Ẑ)表示S由Ẑ生成的可能性。 定义2(基于概率后缀树的生成模型)给定记忆长度l,间隔约束γ和支持度阈值minSup。概率后缀树中任一节点表示的序列模式S,若满足如下条件,称概率后缀树为序列样本集合D的生成模型: 条件1Sup(S,D,γ)≥minSup 条件2|S|≤l 给定样本集合D,查询序列S和质量评价阈值θ,本文目标在于训练得到满足定义2的生成模型Ẑ,通过计算S由Ẑ生成可能性L(S|Ẑ)与S由随机模型生成可能性的比值,进行数据质量评价。具体地,若比值大于θ则认为S的质量可接受。 表2给出了本文所使用的重要符号及其含义。 Table 2 Summary of notations表2 符号汇总 在数据挖掘领域,数据质量直接影响挖掘效果和意义,数据质量评价算法可以对待分析的数据进行质量评估,因而受到广泛关注。文献[5]对非结构化数据进行质量评价,对受控词汇定义了26种数据质量问题,并利用函数对数据质量进行衡量,发现潜在的数据质量问题。除此之外,大多数学者对结构化数据的数据质量进行了研究[6]。文献[7]针对结构化数据进行质量评价,利用给定的用户信息对系统数据质量进行改进,提高了查询结果的质量。文献[8]研究了在实际信息系统中适用的综合性数据质量评估方法,并提出了基于性质的数据质量评估框架。文献[9]提出了函数依赖于条件约束的数据修复方法。与传统统计方法相比,本文考虑序列出现的先后顺序,建立序列数据的生成模型,进而利用生成模型对查询序列进行质量评价。 序列数据中各元素之间的位置,蕴含着丰富的信息,各元素出现的先后位置信息存在某种潜在的规律或者满足某个特殊的分布。针对序列数据具有短暂记忆性特征,文献[3]提出记忆长度概念,即:给定序列S=S[1]S[2]…S[|S|],P(S[|S|]|S[1]S[2]…S[|S|-1])表示子序列S[1]S[2]…S[|S|-1]之后出现S[|S|]的概率,若存在记忆长度l,P(S[|S|]|S[1]S[2]…S[|S|-1])≈P(S[|S|]|S[|S|-l]S[|S|-l+1]…S[|S|-1])(1≤l≤n-1)。为了直接使用高阶马尔科夫链模型,文献[3]提出利用概率后缀树来模拟变化的记忆长度。文献[10]针对铁路数据利用概率后缀树进行离群点检测。文献[11]利用概率后缀树与支持向量机对数据进行分类。 为有效提高序列模式的适应性,挖掘序列模式时通常会考虑间隔约束。文献[12]提出了产生序列前缀和后缀的PrefixSpan算法。文献[13]在PrefixSpan算法的基础上,提出了带间隔约束的序列模式挖掘算法。文献[14]设计了利用带间隔约束的序列模式评价软件缺陷特征的方法。 Spark框架于2011年提出,现已成为流行的并行框架[15]。文献[16]对Spark上交互式数据进行快速处理和分析,并对Spark和Hadoop性能进行比较。文献[17-18]利用Spark进行大规模频繁项集的并行挖掘分析。文献[19]利用Spark框架对海量天文图像进行快速处理。文献[20]利用Spark SQL研究计算过程中的内存崩溃问题。文献[21]利用Spark对药物不良反应数据库进行并行查重。 给定序列样本集合D,查询序列S,记忆长度l,间隔约束γ和最小支持度阈值minSup,本文提出基于Spark的序列数据质量评价算法STALK。 图1给出了STALK算法的流程。可以看出,STALK算法主要步骤包括:步骤①,启动STALK算法,并从HDFS(Hadoop distributed file system)中载入数据到Spark集群,完成数据预处理;步骤②,在Spark框架下,根据定义2训练生成模型Ẑ,当候选序列模式的长度大于l时执行步骤④,否则执行步骤③;步骤③,调用Spark的工作集群,计算每个候选序列模式的匹配度,并计算评价其支持度;步骤④,计算S由Ẑ生成可能性L(S|Ẑ)与S由随机模型生成可能性的比值,评价数据质量。 Fig.1 Flowchart of STALK图1 STALK算法流程 4.1 STALK算法生成概率后缀树 用S表示概率后缀树中当前访问的节点表示的序列模式,S′为包含S为连续子序列的序列模式。若S的支持度满足Ẑ的生成条件1,则将其节点保存至概率后缀树中;否则,根据定理1,S′的支持度Sup( 剪枝条件1(最小支持度剪枝)给定样本集合D,间隔约束γ,若序列S的支持度Sup( 记忆长度l限定了概率后缀树的深度,即后缀树中节点表示的序列模式的长度。如图2所示,给定l=3,则后缀树中各节点表示的序列S的长度|S|≤3。由此可得剪枝条件2[2]。 剪枝条件2(记忆长度剪枝)若概率后缀树中节点表示的序列模式的长度大于记忆长度l,则将该节点及其子节点从概率后缀树中移除。 在生成概率后缀树时,Spark集群计算节点的任务是计算概率后缀树中每个节点表示的候选序列模式的匹配度,并根据剪枝条件1、剪枝条件2进行剪枝,最终建立满足定义2的概率后缀树。根据定义2和剪枝条件1、剪枝条件2,算法1描述了建立概率后缀树的伪代码。 算法1建立概率后缀树Build(D,Σ,γ,l,minSup) 输入:数据质量可靠的序列样本集合D,元素集合Σ,间隔约束γ,最小支持度阈值minSup,记忆长度l 输出:概率后缀树PST 1.PST←∅;Set←∅;Ck←∅;//初始化PST,Set,Ck 2.Ck←Σ;//生成第一层候选模式集合 3.k=1;//k描述当前后缀树的深度 4.While(k≤l)do 5.Set←map(getMatch(Ck,γ));//匹配候选模式 6. 移除Set中不满足剪枝条件1的候选序列模式; 7. ForS∈Set.collect()do//更新概率后缀树 8.PST←PST∪{S}; 9. EndFor 10.Ck←Generate(Ck);//算法2 11.k←k+1; 12.EndWhile 13.ReturnPST; 在算法1中,PST表示概率后缀树,Set表示候选模式集合,Ck表示底层候选模式集合。首先通过步骤2由Σ生成第一层候选模式集合;步骤3用k来描述树的深度,即候选序列模式的最大长度;步骤4~12将满足剪枝条件1的候选模式保存至PST中,最终生成满足定义2的概率后缀树。其中,get-Match函数计算候选序列模式的转移概率,Generate函数生成下一层概率后缀树的候选模式。 利用长度为l的候选模式生成长度为l+1的候选模式时,容易想到采用遍历集合枚举树的方式。传统的完全遍历枚举树方法是把每个候选模式与候选元素集合逐一匹配,这样会造成不必要的计算开销。而深度优先遍历集合枚举树[22]会一次生成候选模式S及其所有包含S为连续子序列的候选模式,但利用剪枝条件移除不符合条件的候选模式的同时,Spark集群会计算所有候选序列模式的匹配度,这样会造成不必要的计算开销,浪费计算资源。 广度优先遍历策略在生成长度为l的候选序列模式之前会生成所有长度小于l的候选模式,Spark集群可以并行处理所有长度为l的候选序列模式,这样可以提高算法效率。因此,采用广度优先遍历集合枚举树方式来生成PST中所有候选模式。算法2给出了STALK生成候选模式的算法伪代码。 算法2候选模式生成Generate(Ck) 输入:概率后缀树上第k层的候选序列模式集合Ck 输出:概率后缀树上第k+1层的候选序列模式集合Ck+1 1.Ck+1←∅;//初始化Ck+1 2.For eachP∈Ckand eachQ∈Ckdo 3. IfSuf(P)=Pre(Q)then 4.Ck+1←Ck+1∪Apd(P,Q[|Q|]); 5. EndIf 6.EndFor 7.ReturnCk+1; 算法2生成候选模式的过程类似于广度优先遍历集合枚举树。即对两个长度为l且其后缀、前缀相同的模式,通过拼接操作生成长度为l+1的候选模式。例如,对ba和ab,由于Suf(ba)=Pre(ab),则生成新的候选模式bab。 4.2 序列转移概率并行计算 通过算法1得到了概率后缀树PST,概率后缀树中任意节点的转移向量为{P1,P2,…,P|Σ|},Pr(1≤r≤|Σ|)表示当前节点转移到下一子节点的概率,其中转移概率P计算如下[2]: 式(2)中分子表示元素e和序列S组成的新序列在D中的匹配度之和,分母表示元素集合Σ中的所有元素和序列S分别组成的序列在D中的匹配度之和。为避免概率为0,公式进行拉普拉斯平滑处理。 例3在表1中,序列aa、ba满足的间隔约束γ=[0,1]的实例个数分别为5和11,则序列a转移到序列aa的概率为(5+1)/(11+5+2)≈0.33。 根据表1中的样本集合,在满足l=2,γ=[0,1],minSup=0.85的条件下生成概率后缀树,如图2所示。节点aaa的支持度小于minSup,根据剪枝条件1,aaa及其子节点从后缀树中移除。根据式(2),可以得到由后缀树中每一个节点转移至子节点的概率。算法3给出图2中转移概率的计算方法。 Fig.2 Probability suffix tree generated by Table 1图2 根据表1序列建立的概率后缀树 算法3PST上节点的转移概率计算getMatch (S′,γ) 输入:序列S′,间隔约束γ 输出:S′及其转移概率P 1.num←0;//num用来保存S′在样本序列上的匹配度 2.sum←0;//sum用来保存S′在D中的匹配度 3.For each sequenceS∈Ddo 4. IfS′⊆γSthen 5. 利用Spark集群计算S′在S的匹配度; 6. EndIf 7.EndFor 8.(S′,sum)←reduceByKey(S′,num);//S′在D中匹配度 9.(S′,P)←map(S′,sum);//计算S′的转移概率 10.Return(S′,P); 观察算法3,步骤3~步骤7利用Spark集群计算S′在每个序列样本上的匹配度;步骤8利用reduce-ByKey操作对S′在序列样本上的匹配度相加,最终得到S′在原始样本集合D的匹配度;步骤9进行map操作得到S′在D上的转移概率。 STALK算法中序列转移概率计算过程(即算法1中步骤5~11)如图3所示。包括3个步骤:步骤①,Spark集群利用textfile操作载入序列样本集,进行数据预处理;步骤②,利用Spark中map操作对序列样本进行候选模式匹配,并通过flatMap、reduceByKey和map操作生成候选序列模式及其转移概率;步骤③,通过collect操作生成该层满足剪枝条件1、剪枝条件2的候选模式集合,最终将序列模式及其转移概率保存至概率后缀树中。 Fig.3 Transition probability prcoss in STALK图3 STALK中转移概率计算过程 4.3 查询序列的数据质量估计方法 通过得到的训练模型Ẑ,给定序列S=S[1]S[2]…S[|S|],用L(S|Ẑ)来衡量生成S的可能性。由贝叶斯后验概率方法得L(S|Ẑ)=P(S[1])P(S[2]|S[1])…P(S[|S|]|S[1]S[2]…S[|S|-1])。根据记忆长度l,由马尔科夫链模型可知L(S|Ẑ)≈P(S[1]) P(S[2]|S[1])…P(S[l+1]|S[1]S[2]…S[l])…P(S[|S|]|S[|S|-l]S[|S|-l+1]…S[|S|-1])。 例4若查询序列S=abba,计算图2中表示的概率后缀树生成S的概率。由贝叶斯后验概率可知L(S|Ẑ)=P(a)P(b|a)P(b|ab)P(a|abb)≈P(a)P(b|a)P(b|ab) P(a|bb)≈0.46×0.67×0.58×0.61≈0.109。 假设序列中各元素相互独立,则生成S的概率为计算如下所示: 用L(S|Ẑ)与R(S)的比值Score来衡量序列的质量可接受度[2]。给定阈值θ,若Score≥θ,则序列S的质量可接受。 例5考虑例4中S=abba,θ=1.0。根据式(4),R(S)=P(a)P(b)P(b)P(a)=0.46×0.54×0.54×0.46≈0.062。由例4,L(S|Ẑ)≈0.109。Score=0.109/0.062≈1.758>θ。因此,序列S的质量可接受。 4.4 Spark下的数据分发和共享策略 为适应基于内存的Spark框架,STALK算法在内存中存储概率后缀树,即各候选序列模式及其转移概率,且主节点每次任务分发时将概率后缀树底层的所有节点分发出去,降低了通信开销。 在建立概率后缀树过程中,每个计算节点分片计算新的序列模式匹配度,有两种剪枝方案: 方案1计算节点剪枝。 方案2主节点剪枝。 根据数据规模大小和并行操作的特性,STALK算法选用方案1,即每个计算节点上进行剪枝操作,这样可以减低主节点对数据集的操作耗时。在数据分发时,分片数目需大于CPU内核数,选取线程数目为分片数目,以提高CPU使用率。本文实验采用8个计算节点,分成64片。此外,使用广播变量和累加器(Spark框架的两种共享变量)降低通信开销,本文将γ、minSup、l作为广播变量,概率后缀树作为累加器。 实验算法由Python语言实现,实验节点配置为Intel Core i7,16 GB内存,Ubuntu14.0.4操作系统,Spark1.6.0版本。本文采用UCI机器学习数据集[23]中基因序列数据集SpliceEI、SpliceIE、SpliceN来验证STALK算法的有效性、执行效率和可扩展性;采用SpliceIE、Activity、Location数据集[24-25]和蛋白质ABC-2族的APF01061数据集验证序列元素集合对STALK执行效率的影响。实验数据集如表3所示。算法参数默认值为l=2,γ=[0,1],minSup=0.85,计算节点数为8。 Table 3 Characteristics of experimental data sets表3 实验数据集特征 5.1 算法有效性验证 令|D-|表示数据质量可接受的序列样本条数数;|D+|表示数据质量可接受的序列样本条数;|SD-|表示数据质量不可接受且被STALK正确判断的序列条数;|SD+|表示数据质量可接受且被STALK正确判断的序列条数。定义查准率Acc=(|SD-|+|SD+|)/(|D-|+|D+|),查全率Rec=|SD-|/|D-|。为验证STALK算法的有效性,用STALK算法分别生成数据集SpliceEI、SpliceIE、SpliceN的训练模型。然后对它们用以下策略生成2×103条测试样本。 策略1对长度相同的候选模式按照转移概率从大到小排序,根据转移概率的值将[0,1]分为不同的小区间;然后利用Python的random函数,生成随机数r(r∈[0,1]),根据r的大小匹配各个区间,匹配成功则转移至该节点;最终生成1×103条质量可接受的SpliceEID+、SpliceIED+、SpliceND+集合。 策略2在与策略1相同的生成条件下,利用随机数r匹配区间,与策略1不同的是,匹配成功则转移至对应小区间的节点,生成1×103条质量不可接受的SpliceEID-、SpliceIED-、SpliceND-集合。 用SpliceEID+∪SpliceEID-,SpliceIED+∪SpliceIED-,SpliceND+∪SpliceND-分别组成测试数据SpliceEID、SpliceIED、SpliceND。为验证STALK算法能否有效检测到质量不可接受的序列样本,分别用SpliceEI、SpliceIE、SpliceN作为训练集,利用STALK算法生成模型,对SpliceEID、SpliceIED、SpliceND进行质量评价。表4给出θ改变时STALK算法在各数据集上的数据质量评价结果,观察得,STALK算法能有效查找出数据质量不可接受的序列。 Table 4 Results of STALK on test data sets表4 STALK算法对测试数据集的结果 5.2 算法执行效率验证 为验证STALK算法的执行效率,对比SQEPST算法[2]和STALK算法的执行时间。本文按照策略1对SpliceIE样本数据集合成2×104、4×104、6×104、8× 104条数据建立生成模型Ẑ的执行时间,如图4所示。 Fig.4 Comparison of runtime between STALK and SQEPST图4 STALK与SQEPST算法的运行时间比较 图4中,随着数据集规模的增大,STALK算法和SQEPST算法的执行时间逐渐增加,然而STALK算法的执行效率远优于SQEPST算法。特别是,SQEPST算法在数据规模为4×104条时内存溢出。分析原因如下:随着数据集规模增大,候选序列模式集合增大,SQEPST算法匹配度计算开销增加;此外,深度优先遍历集合枚举树不能及时剪枝,增加了计算资源开销。 为分析间隔约束γ、记忆长度l对建立生成模型时间的影响,按照策略1对3个基因序列数据集合成5×105条数据。观察图5~图7中(a)图,随着γ的增大,算法执行时间增大。分析原因如下:γ决定候选模式的匹配集合长度,当γ增大时,匹配集合长度增加,因此算法执行时间增加。观察图5~图7中(b)图,随着l的增大,算法执行时间增大。分析原因如下:记忆长度决定概率后缀树的深度,l增大时,概率后缀树的深度增大,因此算法执行时间增加。 5.3 算法可扩展性验证 为验证STALK算法的可扩展性,按照策略1对3个基因序列数据集合成5×105条数据,分析计算节点数目对建立生成模型时间的影响。观察图5~图7中(c)图,随着节点数目增加,STALK算法执行时间显著降低。原因为给定数据条数,主节点根据计算节点数目分发任务。因此增加节点数,各节点的数据分片会减少,相应各计算节点的执行时间减小,总时间减小。为验证数据规模对算法可扩展性的影响,按照策略1分别将3个基因数据集的规模合成为2× 106、4×106、6×106、8×106、10×106。观察图5~图7中(d)图,随着数据规模增大,算法执行时间增加。原因为当数据规模增大时,算法需要在更多序列样本上计算候选模式的匹配度和支持度,因此执行时间增长。 Fig.5 Runtime of STALK on synthetic data set by SpliceEI图5 在SpliceEI合成数据集上STALK算法的运行时间 Fig.6 Runtime of STALK on synthetic data set SpliceIE图6 在SpliceIE合成数据集上STALK算法的运行时间 Fig.7 Runtime of STALK on synthetic data set SpliceN图7 在SpliceN合成数据集上STALK算法的运行时间 5.4 |Σ|对算法执行效率的影响 在建立概率后缀树过程中,元素个数决定每一层节点个数,观察图5~图7,3个数据集的|Σ|都为4,故相同条件下算法运行时间相似。为验证|Σ|对算法执行时间的影响,按照策略1将SpliceIE、Activity、Location、APF01061各自生成5×105条合成数据集。从图8中可得,增大|Σ|,算法执行时间增加。从图8(b)看出,增大minSup会缩小样本集合中符合条件的序列筛选范围,因此执行时间降低。 Fig.8 Runtime of STALK on data sets with different|Σ|图8 STALK算法在含有不同|Σ|的数据集上的运行时间 数据质量评价的传统方式是定性分析,缺少利用生成模型对大规模数据质量的分析。针对该问题,本文提出了基于Spark的序列数据质量评价算法STALK。STALK算法利用质量可靠的序列样本集合高效建立生成模型,并根据生成模型快速评价查询数据质量,并且采用改进的剪枝策略优化了算法在Spark平台的执行效率。通过大规模序列数据集验证了算法的有效性、执行效率和可扩展性。 下一步,将增加Spark集群中计算节点数量,使STALK适用于更大规模的数据分析。同时,考虑更多实际应用中对STALK算法有效性、执行效率和可扩展性的验证;设计STALK算法在不同领域的应用,尝试将其运用到理财投资中,分析个人理财习惯并对理财产品进行推荐,利用序列质量评价进行DNA异常序列检测。 References: [1]Guo Zhimao,Zhou Aoying.Research on data quality and data cleaning:a survey[J].Journal of Software,2002,13 (11):2076-2082. [2]Wang Huifeng,Duan Lei,Hu Bin,et al.Design of evaluating sequential data quality with gap constraint[J].Journal of Frontiers of Computer Science and Technology,2015,9 (10):1180-1194. [3]Ron D,Singer Y,Tishby N.The power of amnesia:learning probabilistic automata with variable memory length[J].Machine Learning,1996,25(2/3):117-149. [4]Zaharia M,Chowdhury M,Franklin M J,et al.Spark:cluster computing with working sets[C]//Proceedings of the 2nd USENIX Conference on Hot Topics in Cloud Computing, Boston,USA,Jun 22-25,2010.Berkeley,USA:USENIX Association,2010:1765-1773. [5]Suominen O,Mader C.Assessing and improving the quality of SKOS vocabularies[J].Journal on Data Semantics,2014, 3(1):47-73. [6]Carlo B,Daniele B,Federico C,et al.A data quality methodology for heterogeneous data[J].International Journal of Database Management Systems,2011,3(1):60-79. [7]Meng Xiao,Wang Hongzhi,Gao Hong,et al.bibEOS:a social system of bibliography retrieval and management[J]. Journal of Frontiers of Computer Science and Technology, 2010,4(1):54-63. [8]Ding Xiaoou,Wang Hongzhi,Zhang Xiaoying,et al.Association relationships study of multi-dimensional data quality [J].Journal of Software,2016,27(7):1626-1644. [9]Jin Cheqing,Liu Huiping,Zhou Aoying.Functional dependency and conditional constraint based data repair[J].Journal of Software,2016,27(7):1671-1684. [10]Rabatel J,Bringay S,Poncelet P.Anomaly detection in monitoring sensor data for preventive maintenance[J].Expert Systems withApplications,2011,38(6):7003-7015. [11]Lu Kefa,Cao Qing,Thomason M.Bugs or anomalies?sequence mining based debugging in wireless sensor networks [C]//Proceedings of the 9th International Conference on Mobile Ad-Hoc and Sensor Systems,Las Vegas,USA,Oct 8-11,2012.Washington:IEEE Computer Society,2012:463-467. [12]Pei Jian,Han Jiawei,Mortazavi-Asl B,et al.PrefixSpan: mining sequential patterns efficiently by prefix-projected pattern growth[C]//Proceedings of the 17th International Conference on Data Engineering,Heidelberg,Germany, Apr 2-6,2001.Washington:IEEE Computer Society,2001: 215-224. [13]Antunes C,Oliveira A L.Generalization of pattern-growth methods for sequential pattern mining with gap constraints [C]//LNCS 2734:Proceedings of the 3rd International Conference on Machine Learning and Data mining in Pattern Recognition,Leipzig,Germany,Jul 5-7,2003.Berlin,Heidelberg:Springer,2003:239-251. [14]Sun Pei,Chawla S,Arunasalam B.Mining for outliers in sequential databases[C]//Proceedings of the 6th SIAM International Conference on Data Mining,Bethesda,USA,Apr 20-22,2006.Philadelphia,USA:SDM,2006:94-106. [15]Zaharia M,Chowdhury M,Das M,et al.Resilient distributed datasets:a fault-tolerant abstraction for in-memory cluster computing[C]//Proceedings of the 9th USENIX Conference on Networked Systems Design and Implementation,San Jose, USA,Apr 25-27,2012.Berkeley,USA:USENIX Association,2012:141-146. [16]Zaharia M,Chowdhury M,Das T,et al.Fast and interactive analytics over Hadoop data with Spark[J].USENIX Login, 2012,37(4):45-51. [17]Qiu Hongjian,Gu Rong,Yuan Chunfeng,et al.YAFIM:a parallel frequent itemset mining algorithm with Spark[C]// Proceedings of the 2014 IEEE International Parallel&Distributed Processing Symposium Workshops,Phoenix,USA, May 19-23,2014.Washington:IEEE Computer Society,2014: 1664-1671. [18]Zhang Feng,Liu Min,Gui Feng,et al.A distributed frequent itemset mining algorithm using Spark for big data analytics[J].Cluster Computing,2015,18(4):1493-1501. [19]Zhang Zhao,Barbary K,Nothaft F A,et al.Scientific computing meets big data technology:an astronomy use case [C]//Proceedings of the 2015 International Conference on Big Data,Santa Clara,USA,Oct 29-Nov 1,2015.Piscataway,USA:IEEE,2015:918-927. [20]Rao P S,Porter G.Is memory disaggregation feasible?a case study with Spark SQL[C]//Proceedings of the 2016 Symposium on Architectures for Networking and Communications Systems,Santa Clara,USA,Mar 17-18,2016. New York:ACM,2016:75-80. [21]Wang Chen,Karimi S.Parallel duplicate detection in adverse drug reaction databases with Spark[C]//Proceedings of the 19th International Conference on Extending Database Technology,Bordeaux,France,Mar 15-18,2016:551-562. [22]Wang Xianming,Duan Lei,Dong Guozhu,et al.Efficient mining of density-aware distinguishing sequential patterns with gap constraints[C]//LNCS 8421:Proceedings of the 19th International Conference on Database Systems for Ad-vanced Applications,Bali,Indonesia,Apr 21-24,2014.Berlin,Heidelberg:Springer,2014:372-387. [23]Lichman M.UCI machine learning repository[EB/OL].Irvine,CA:University of California,School of Information and Computer Science(2013)[2015-03-20].http://archive. ics.uci.edu/ml. [24]Ordóñez F J,Toledo P,Sanchis A.Activity recognition using hybrid generative/discriminative models on home environments using binary sensors[J].Sensors,2013,13(5):5460-5477. [25]Yang Hao,Duan Lei,Hu Bin,et al.Mining top-kdistinguishing sequential patterns with gap constraint[J].Journal of Software,2015,26(11):2994-3009. 附中文参考文献: [1]郭志懋,周傲英.数据质量和数据清洗研究综述[J].软件学报,2002,13(11):2076-2082. [2]王慧锋,段磊,胡斌,等.带间隔约束的序列数据质量评价算法设计[J].计算机科学与探索,2015,9(10):1180-1194. [7]孟啸,王宏志,高宏,等.bibEOS:一个高质量的社会化文献检索与管理系统[J].计算机科学与探索,2010,4(1):54-63. [8]丁小欧,王宏志,张笑影,等.数据质量多种性质的关联关系研究[J].软件学报,2016,27(7):1626-1644. [9]金澈清,刘辉平,周傲英.基于函数依赖与条件约束的数据修复方法[J].软件学报,2016,27(7):1671-1684. [25]杨皓,段磊,胡斌,等.带间隔约束的Top-k对比序列模式挖掘[J].软件学报,2015,26(11):2994-3009. HAN Chao was born in 1994.He is an M.S.candidate at School of Computer Science,Sichuan University,and the student member of CCF.His research interests include data mining and knowledge engineering. 韩超(1994—),男,甘肃庆阳人,四川大学计算机学院硕士研究生,CCF学生会员,主要研究领域为数据挖掘,知识工程。 段磊(1981—),男,四川成都人,2008年于四川大学计算机应用技术专业获得博士学位,现为四川大学副教授、硕士生导师,CCF高级会员,主要研究领域为数据挖掘,健康信息学,进化计算。 DENG Song was born in 1980.His research interests include distributed data mining,smart grid information security and physical fusion system of electric power information. 邓松(1980—),男,安徽合肥人,博士,高级工程师,主要研究领域为分布式数据挖掘,智能电网信息安全,电力信息物理融合系统。 WANG Huifeng was born in 1988.He received the M.S.degree in computer science from Sichuan University in 2016.His research interests include data mining and knowledge engineering. 王慧锋(1988—),男,河南南阳人,2016年于四川大学计算机科学与技术专业获得硕士学位,主要研究领域为数据挖掘,知识工程。 TANG Changjie was born in 1946.He is a professor and Ph.D.supervisor at Sichuan University,and the distinguishing member of CCF.His research interests include database technique and data mining. 唐常杰(1946—),男,重庆人,四川大学教授、博士生导师,CCF杰出会员,主要研究领域为数据库技术,数据挖掘。 Evaluation of Sequential Data Quality Using Spark* HAN Chao1,DUAN Lei1,2+,DENG Song3,WANG Huifeng1,TANG Changjie1 Sequential data are prevalent in many real world applications.The quality evaluation on sequential data, which attracts the attentions from both academic research and industry fields,is important and prerequisite for extracting knowledge from the sequential data.Recently,a method using the probabilistic suffix tree has been proposed for evaluating the sequential data quality.However,this method cannot deal with the large-scale data set.To break this limitation,this paper proposes a Spark-based algorithm,called STALK(sequential data quality evaluation with Spark),for evaluating the quality of large-scale sequential data.Moreover,this paper uses the novel pruning strategies to improve the efficiency of STALK.Specifically,on the Spark platform,the large-scale sequential data are efficiently used to generate model,and the data quality of query sequence can be evaluated according to the generated model rapidly.Experiments on real-world sequential data sets demonstrate that STALK is effective,efficient and scalable. was born in 1981.He the Ph.D.degree in computer science from Sichuan University in 2008. Now he is an associate professor and M.S.supervisor at Sichuan University,and the senior member of CCF.His research interests include data mining,health-informatics and evolutionary computation. A TP391 *The National Natural Science Foundation of China under Grant Nos.61572332,51507084(国家自然科学基金);the Postdoctoral Science Foundation of China under Grant Nos.2016T90850,2016M591890(中国博士后科学基金);the Fundamental Research Funds for the Central Universities of China under Grant No.2016SCU04A22(中央高校基本科研业务费专项资金). Received 2016-08,Accepted 2016-10. CNKI网络优先出版:2016-10-18,http://www.cnki.net/kcms/detail/11.5602.TP.20161018.1622.018.html Key words:data quality;probabilistic suffix tree;Spark;parallel computing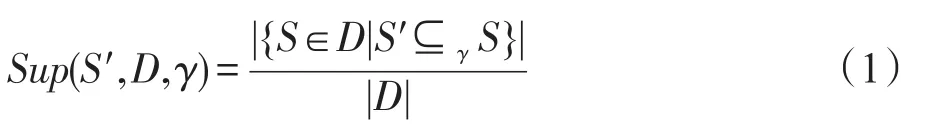

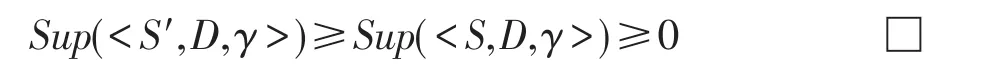

3 相关工作
4 STALK算法设计
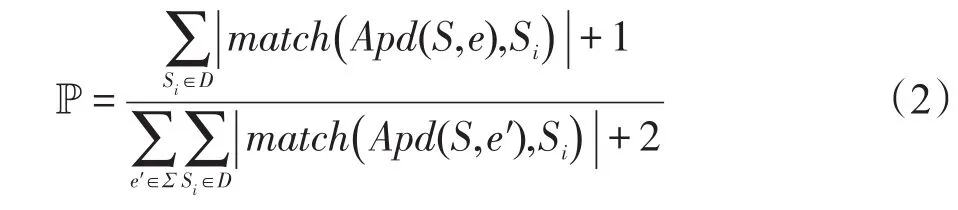

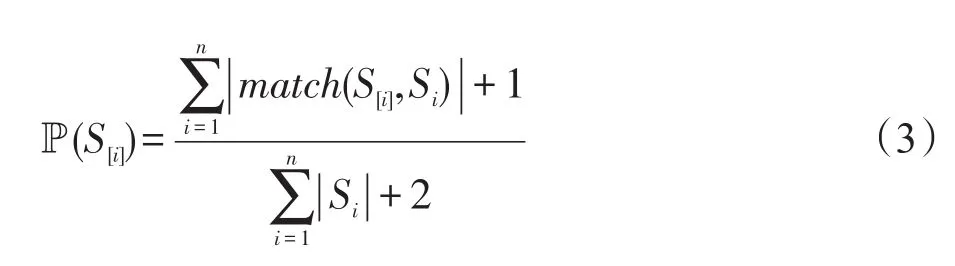

5 实验

6 结束语





1.School of Computer Science,Sichuan University,Chengdu 610065,China
2.West China School of Public Health,Sichuan University,Chengdu 610041,China
3.Institute ofAdvanced Technology,Nanjing University of Posts and Telecommunications,Nanjing 210003,China
+Corresponding author:E-mail:leiduan@scu.edu.cn

