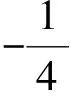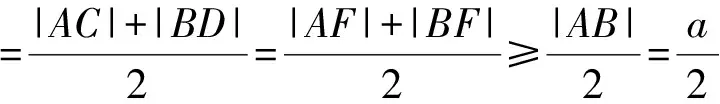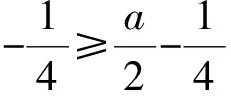以形助数之小心翼翼*

●王 博 陈华云 (温州市第二外国语学校 浙江温州 325015)



以形助数之小心翼翼*

●王 博 陈华云 (温州市第二外国语学校 浙江温州 325015)

数形结合思想作为四大数学思想方法之一，在解题过程中发挥着巨大的作用.但图形毕竟只是直观认知的工具，它不能替代逻辑证明.文章结合实际教学经历，分选不同章节，从不同角度谈谈以形助数的缺陷、错因分析以及如何克服易错点.

数形结合；谬误；逻辑

数形结合是重要的数学思想之一，借助于形的直观，我们能在数的迷雾中看得更真切，时有“拨开云雾见青天”之感.笔者从以形助数的缺陷出发，明示错误，反思错因，从而纠正思维、操作上的谬误，提高数形结合思想方法的理性认识.

案例1 图像特征的认识偏差

例1 设函数f(x)=x2+ax+b(其中a,b∈R).

2)已知函数f(x)在[-1,1]上存在零点，且0≤b-2a≤1，求b的取值范围.

(2015年浙江省数学高考文科试题第20题)

错解 由题意知

f(-2)=4-2a+b，

由

0≤b-2a≤1，

得

4≤f(-2)≤5.

又因为f(0)=b，所以问题转化为“函数f(x)=x2+ax+b在x∈[-1,1]上存在零点，且4≤f(-2)≤5，求f(0)的取值范围”.如图1，考虑抛物线与2条线段AB,CD均产生交点.由图像可知，当抛物线经过点A,D时，f(0)有最小值，此时

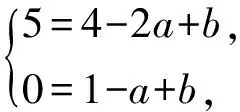
得

b=-3.

当抛物线经过点B,D时，f(0)有最大值，此时

得

但是，结果跟构图一致吗？如图2所示，当抛物线经过点B,D时，f(0)的最大值为某一正数.当数形结合出现矛盾时，孰对孰错？若代数结果不能体现几何特征，它所对应的函数图像是怎样的呢？当我们随手画下抛物线时，这样的抛物线是否满足题意呢？

图1 图2

那么图像该如何放置才能得到b=f(0)的最大值？不妨考虑抛物线经过点D且与x轴相切的情况，如图4所示，此时

解得

图3 图4

上述案例提醒我们：作图时除了要考虑图形的一般特征(如零点、定点)外，还需要充分结合图形的其他特征(如凹凸性、拐点).由于对图形特征(这里指的是抛物线的开口大小)的感知不准确，可能会误作草图，从而走入歧途.

案例2 毫厘之处的认知困难

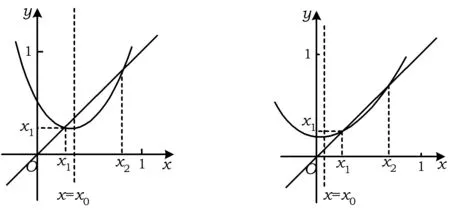
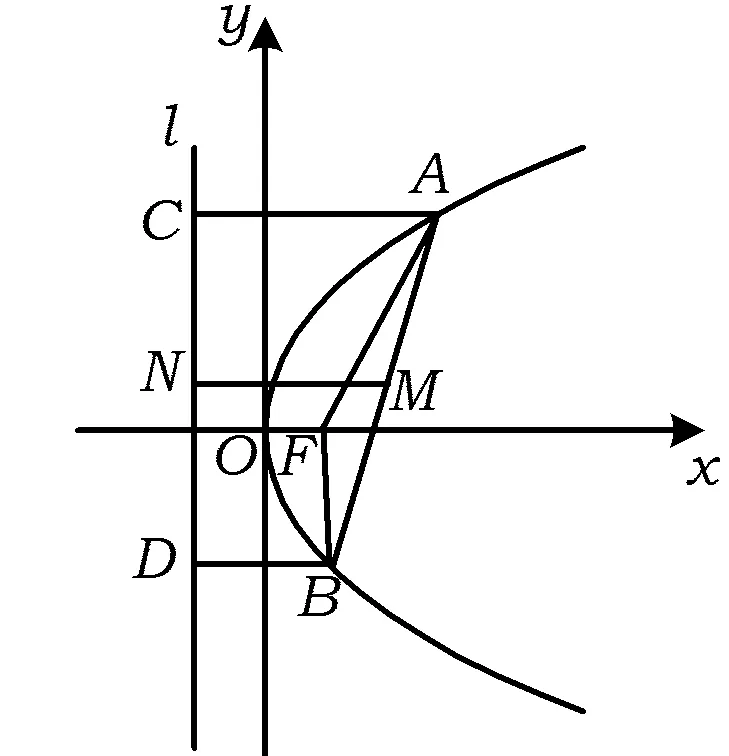
例2 已知二次函数f(x)=x2+bx+c，方程f(x)-x=0的2个根x1，x2满足0

1)当x∈(0,x1)时，证明：x

(2015年浙江省数学学考模拟试题第22题)

分析 方程f(x)-x=0的根可视作函数y=f(x)与y=x图像交点的横坐标.根据题意作出图形(如图5)，从图中可以观察到这样的信息：

①当x∈(0,x1)时，x

②设函数f(x)的图像关于直线x=x0对称，则x1

这与我们要证明的命题不相符！

在考试过程中，笔者所任教班级有80%的学生作出了类似的草图.由于与论题相悖，因此在尝试构建满足题意的图形上花费了大量时间，当摸索得到图6时，心中依然充满困惑：图像在(0,1)上的单调性如何？图5为什么不可能存在？

图5 图6

学生产生困惑的原因在于：上述问题研究的区域过于狭小，交点与顶点的位置关系有“失之毫厘,谬以千里”之险.此时若借助于图形解决问题，则犹如螺蛳壳里作道场，难度很大.正如华罗庚先生所言：形缺数时难入微，高见甚是.

正解 根据题意得

f(x)-x=(x-x1)(x-x2)，其中0

1)当x∈(0,x1)时，

(x-x1)(x-x2)>0，

因此

f(x)>x.

由于f(x)=(x-x1)(x-x2)+x，从而

f(x)-x1=(x-x1)(x-x2+1)<0，

即

f(x)

于是

x

2)由于f(x)=x2-(x1+x2-1)x+x1x2，得

案例3 分类讨论的知一漏二

例3[1]设线段AB的2个端点在抛物线y2=x上移动，M为线段AB的中点，|AB|=a(其中a为大于0的常数)，求M到y轴的最短距离.

图7

在直角梯形ABCD中，由梯形中位线定理及抛物线的定义得

从而

上述解法的不足之处在于作图时先入为主，忽视了动弦AB的活动区域受参数a的限制.事实上，上述解法成立的条件是动弦AB必过焦点，经过抛物线焦点的弦中，以通径最短，而抛物线y2=x的通径为1，因此上述解法只有当a=|AB|≥1时才能成立.而当0

正解 设直线AB的方程为x=my+t，A(x1,y1)，B(x2,y2)，联立

消去x，得

y2-my-t=0，

从而

Δ=m2+4t>0.

由韦达定理得

y1+y2=m，x1+x2=m2+2t，

(1)

的最小值.又因为|AB|=a，即

从而

化简得

令p=m2+1≥1，原问题即求

的最小值.

从以上的分析可以看出，当问题需要分类讨论时，仅从图形出发解决问题可能会分类不清，列举不全.

案例4 直观感知的逻辑缺失

( )

A.1 B.2 C.3 D.4

(2013年天津市数学高考理科试题第7题)

图8 图9

因此g(x)在(0,1)上单调递增.而当x→0时，

《课标》中有这样一段话：高中数学课程应注重提高学生的数学思维能力，这是数学教育的基本目标之一.人们在学习数学和运用数学解决问题时，不断地经历直观感知、观察发现、归纳类比、空间想象、抽象概括、符号表示、运算求解、数据处理、演绎证明、反思与建构等思维过程.这些过程是数学思维能力的具体体现，有助于学生对客观事物中蕴涵的数学模式进行思考和作出判断.数学思维能力在形成理性思维中发挥着独特的作用.

笔者通过以上实例，阐明图解法在思维、操作上的谬误，从而引导学生认识到问题的解决既需要图形的支撑，更需要逻辑的把关，让学生学会用理性的思维、实事求是的态度解决问题、认识世界.

[1] 蔡小雄.更高更妙的高中数学思想与方法[M].杭州：浙江大学出版社，2017.

2017-02-14；

2017-03-16

王博(1991-)，男，浙江温州人，中学二级教师.研究方向：数学教育.

O123.1

A

1003-6407(2017)06-18-03