也要重视课堂教学板书*
●崔志荣 (安丰中学 江苏东台 224221)
也要重视课堂教学板书*
●崔志荣 (安丰中学 江苏东台 224221)
数学课堂教学要把握好课件与板书的平衡关系.结合现代化教育技术用好课件,有利于学生的理解,提高课堂教学效果,但这不能完全代替教学板书.良好的板书能体现师生的同步思维,使得知识方法的生成及分析思路的形成自然而然、水到渠成.完整的板书能展示一个清晰明了的知识体系,对学生的宏观认识有促进作用.
教学板书;等差数列;反思
1 板书现状之分析
随着现代教育技术水平的提高,课堂教学形式越来越丰富,教育教学水平也相应提高许多.然而,也出现了一些不好的现象,有部分教师更依赖于多媒体课件教学,他们不重视教学板书;有些教师的板书就像草稿纸,凌乱不堪;有些教师的板书寥寥数语,教学变成了课件的解读;还有些教师的板书主次不分,如此等等.好的板书通常知识脉络清晰,例题的分析过程详略得当,整个板书内容的层次感很强.
运用现代教育技术教学,教学优势明显,毋庸置疑,但这不能完全代替教学板书.教育技术的教学更侧重于某个教学点的处理,如几何画板的运用,它能给出含参曲线的变化趋势,能为我们寻找解题思路提供帮助,是一个教学处理点;完美的板书则主要呈现一节课的教学内容,从知识方法的生成到具体运用,体现了课堂内容研究的整体性.
此外,常听一些教师抱怨学生的书写习惯差,那教师是不是也要反思一下:自己的教学示范性板书做得怎么样呢?优秀的教学板书,对学生的书写习惯、学习习惯会有潜移默化的影响.总之,我们的课堂教学既要用好现代教育技术,以促进学生对数学疑难问题的理解,但不应忽视教学板书.
2 板书实践
关于教学板书的研究文献很少,缺少板书的设计理论支撑.笔者根据自身的教学实践经验,从新授课与复习课这2个方面,结合具体的教学案例,谈谈个人的一些做法,未必完全合理,旨在引起广大教师对教学板书的重视.
2.1 过程性板书
新授课对于学生来说是新生事物,知识方法的构建过程是关键,板书应该充分体现知识方法生成的研究思路.同时,运用这些新知识解决一些应用问题,是学生从无到有的学习过程,板书的示范性很重要.因此,笔者认为新授课的板书应以“过程性”板书为主,还要注意严密性、规范性等细节.笔者以新授课“等差数列的前n项和公式”为例,谈谈板书过程.
课堂导入可从数学家高斯的故事入手,研究高斯计算1+2+3+…+100的方法,并由此提出:高斯的这个“倒序求和”方法是否适用于其他等差数列求和呢?如求和:1+3+5+…+101,让学生思考完成.最后提出:能不能运用“倒序求和”这个方法,研究一般性等差数列的求和呢?即对等差数列{an},求其前n项和Sn=a1+a2+a3+…+an.以上这些内容通常以课件为载体呈现,但接下来的公式推导、演变,还是需要一点板书的,笔者给出如下的板书过程:
由Sn=a1+a2+a3+…+an,
(1)
将式(1)倒序,得
Sn=an+an-1+an-2+…+a1.
(2)
式(1)+式(2),得
2Sn= (a1+an)+(a2+an-1)+(a3+an-2)+…+
(an+a1),
从而
2Sn=n(a1+an),
于是
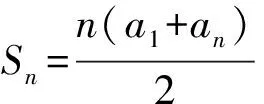
即

公式演变1:将an=a1+(n-1)d代入,整理得
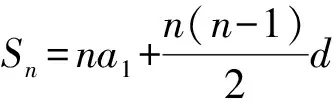
即由基本量a1与d以及项数n,可求和.
公式演变2:整理为关于n的函数得
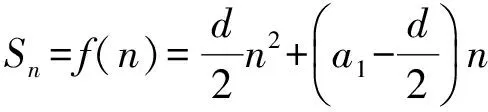
(3)
当d=0时,式(3)是关于n的一次函数;当d≠0时,式(3)是关于n的二次函数.函数f(n)总过原点.
公式的运用教学是课堂教学的重要组成部分.作为新授课,每节课至少应示范一道题的完整解答过程,有些特别简单的题目,可由学生自主练习,投影个别学生的解答解读即可;较难的题目,可借助课件提出问题,引导学生思考分析,课件上形成解题思路后,让学生试着完成,再投影一些学生的优秀解答,分析其关键步骤;教师可以详细板书那些中等难度的题目,让学生体验过程的严密性、规范性等.就本节课而言,可重点板书苏教版教材上的一道例题,教师先用课件展示例题:
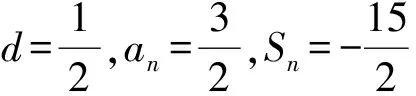
(苏教版《数学(必修5)》第41页例2)
通过分析,容易得到2种方法,作为板书过程,其中解法1与课本一致.笔者板书解法2:
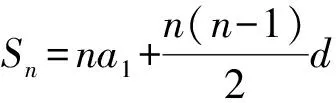
亦可用公式
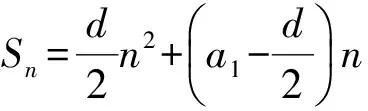
得
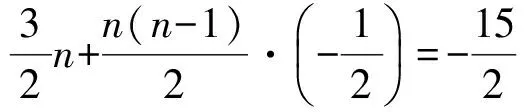
解得
n=10或n=-3(舍去).
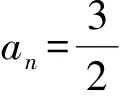
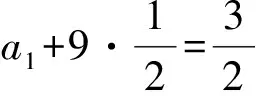
于是
a1=-3.
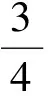
2.2 分析型板书
复习课,尤其是高三数学复习课,更强调知识方法的深入理解,更注重知识方法的综合运用,这与新授课的板书会有所不同.如知识点的复习,若只是简单的流水形式的板书,则对学生的理解没有多大的帮助.教师的板书若能体现知识间的关联、体现一定的知识体系,让学生的理解更深一层,则对学生的灵活运用是有帮助的;例题的讲解,当然还要一些例题的详细解答板书,数学的严密性、规范性要求不能放松,但更要培养学生的分析能力,强调解题的切入点分析、条件与问题的关联等,充分关注思路的生成分析.基于以上分析,无论是知识点分析还是例题的讲解,板书都要体现一定的思考分析,笔者称之为“分析型”板书.
关于知识点复习的板书,笔者以高三一轮复习“向量的数量积”为例,设计了一个公式因果关系的图示(如图1所示).
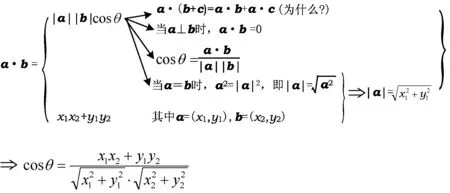
图1
也许有教师认为,图1可以由课件分层次给出.也不能说一定不可以,笔者强调图1板书的目的是让学生体验形成这样一个图示的过程,以促进学生知识点间的关联性理解.课件在这里另有作用,图1的生成需要问题引导,通过课件提出问题能节约时间,如为什么向量的数量积a·b=x1x2+y1y2?学生思考后,得到公式的证明,可通过课件给出严密、详细的过程等等.图1为什么称为“分析型”板书?因为它的生成是教师通过问题的引导,师生共同分析得到的.
复习课例题的讲解,当然还需要解题过程的详细板书,但这只是针对个别题目.大多数题目,我们更关注的是解题分析,这些题目的板书更强调的是分析过程、解题思路、关键步骤等.笔者以例2为例,通过板书说明.
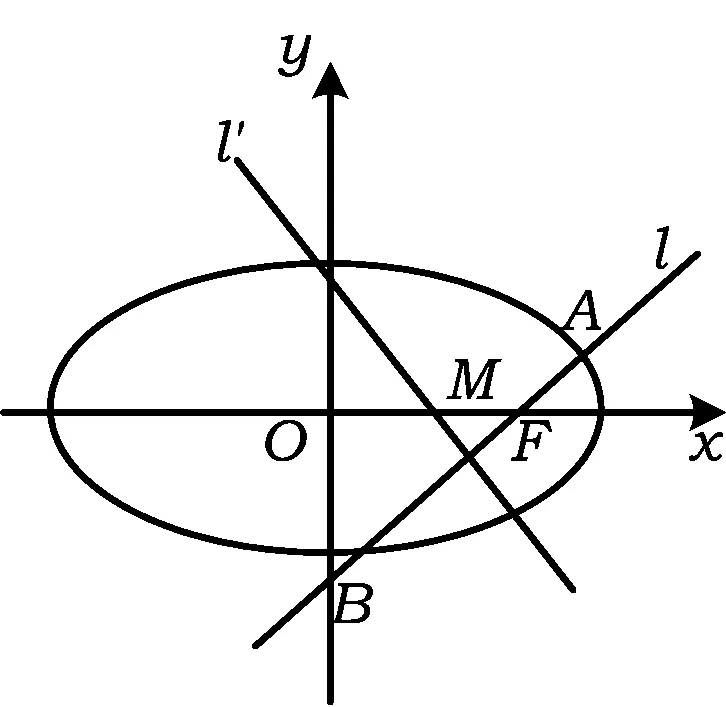
图2
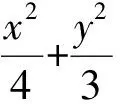
1)若l的斜率为1,求l′的方程;
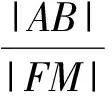
第1)小题学生的正确率比较高,教师可不讲解,重在分析第2)小题,并需要适当的板书进行分析.笔者给出以下2个板书:
板书1 (步骤板书)
第1步:设直线l的方程,与椭圆联立方程组,由韦达定理,可得点A,B的横坐标x1与x2的关系;
第2步:运用椭圆第二定义,推导右焦半径公式,从而可用x1,x2表示线段AB的长,再由第1步的结论,求出线段AB的长;
第3步:借助第1步的结论,求出线段AB的中点,由此可得直线l′的方程,令y=0,可得点M的横坐标,从而求出线段FM的长;
板书1是在教师的启迪之下,学生分析出的思路方法,这种步骤性板书层次感强、目标明确,若长期熏陶,则对提高学生的思维监控意识会有较大的帮助.教学的下一步,要求学生具体完成解答过程,教师课堂巡查时,要注意收集学生的一些典型过程,如精简的规范过程、常见的易错过程等,通过实物投影展示点评.
这个步骤性板书,还可以转化成图1所示的思维流程板书(如图3所示).
板书2

图3
3 反思
数学课堂教学,不应忽视板书教学,无论课件做得多么好,也需要黑板板书.首先,在课堂上,肯定会遇到一些始料未及的学生反馈,学生的想法完全超出教师准备的课件,那就需要板书学生思维过程,与其他学生共同研讨;其次,用课件完全取代传统的教学板书也不合理,课件的教学优势自然不需要说了,但传统的板书,也有它的优势,如它能体现师生的同步思维,使得知识方法的生成、以及分析思路的形成自然而然、水到渠成;它的示范性对学生有潜移默化的影响,好的板书,能够培养学生思维的严密性、作业的规范性;还有一节完整的板书,它展示了一个清晰明了的知识体系,对学生的宏观认识有促进作用.
总之,我们的数学课堂教学,要把握好课件与板书的平衡关系.既不能为用课件而用课件,也不能全不用现代化手段,而是要结合现代化信息技术用好课件,促进学生理解一些疑难问题,通过课件引导学生思考,把学生探究的成果自然地展示在黑板上.因此,教师课前备课要多花时间和精力,板书的设计要有整体框架,具体内容的板书要有预案.长期良好的教学板书,加之现代化技术的运用,教学效果定会大放异彩!
[1] 单墫.苏教版普通高中课程标准实验教科书·数学(必修5)[M].南京:江苏教育出版社,2012.
2017-02-12;
2017-03-13
江苏省教研室第11期重点课题(2015JK11-Z061)
崔志荣(1978-),男,江苏东台人,中学高级教师.研究方向:数学教育.
O12
A
1003-6407(2017)06-11-03

