在分类中辨析数学概念*——以“空间几何体的结构”的教学设计为例

●张 磊 (鄞州高级中学 浙江宁波 315100)



在分类中辨析数学概念*
——以“空间几何体的结构”的教学设计为例

●张 磊 (鄞州高级中学 浙江宁波 315100)

文章通过分类辨析，引导学生学习多面体与旋转体的相关概念，体会认识一个新的数学概念的“基本套路”，鼓励学生自主探究棱柱等几何体的结构特征与相关概念.整个教学设计充分体现“以生为本”，并以宁波本土建筑与世界著名建筑为载体，渗透数学文化，让学生欣赏数学美.

以生为本;渗透学法;数学文化;分类辨析

前不久，浙江省宁波市鄞州区教育局教研室组织了以“生本型课堂”为主题的教研交流活动，内容取材于人教版《普通高中课程标准试验教科书·数学(必修2)》第1.1节“空间几何体的结构”.笔者的教学设计“在分类中辨析数学概念，从生活中领略数学之美”得到了与会教师的一致好评，现将其整理成文，与同行分享.

1 课堂简录

1.1 创设情境,渗透文化

师：许多人认为数学是抽象的，但是伟大的数学家哈尔莫斯说过：“数学之美是很自然明白地摆着的.”首先，让我和大家一起领略明摆着的数学美.

教师通过PPT依次播放宁波的标志性建筑：鄞州银行总行、天一广场的天主教堂、中山西路上的天宁寺塔、天一广场的星巴克咖啡店等，并介绍这些建筑中隐藏的数学美.

师：可能有的学生会问，这些不是建筑吗，跟数学美有什么关系.其实17世纪之前，建筑学一直是应用数学的一部分，因为许多建筑都是以数学中的几何体为模型建造的.你能从讲台上的几何体模型找到这些建筑的雏形吗？

教师事先准备了如图1所示的12个几何体模型实物.请学生上台挑选对应的模型，并进行解释.

师：其实建筑中的美就在于对应的几何体具有美的结构！那么什么是空间几何体呢？

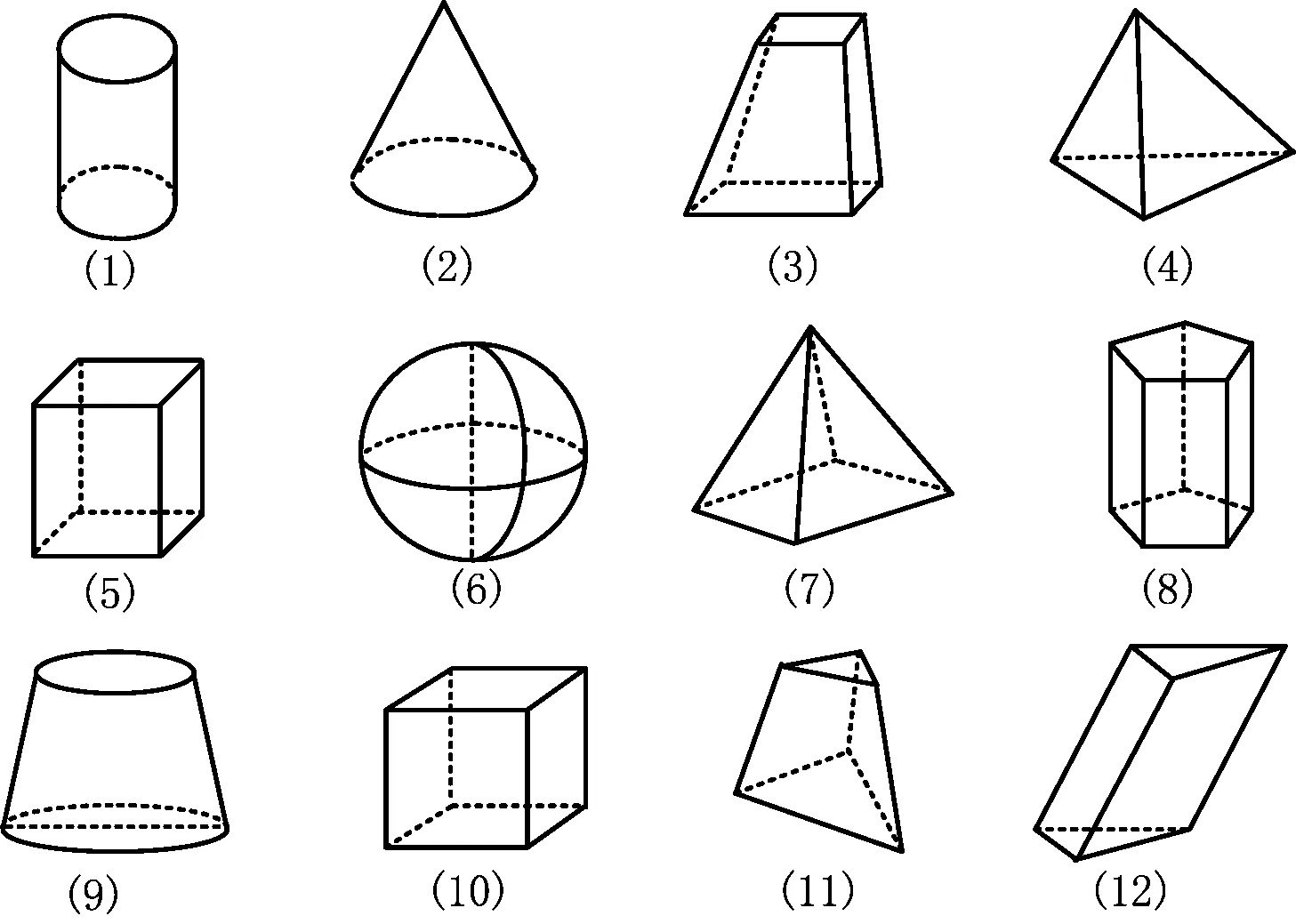
图1

设计意图 从哈尔莫斯的名言引入本节课，设置悬念.上公开课要接地气，贴近学生的实际，这样才能产生共鸣，以宁波的标志性建筑引入情景，一方面让学生发现身边的数学美，学做一位生活的有心人；另一方面，起到了活跃气氛的效果，为后面学生主动参与课堂打下基础，更起到了“让学生了解数学的历史，体会数学的重要性”的目的.

1.2 善于分类，辨析概念

师：如果我们只考虑物体的形状与大小，而不考虑其他因素，那么这些物体抽象出来的空间图形叫做空间几何体.其实，空间几何体还有很多，由于结构不同，它们有各自的美.请大家以小组为单位，根据几何体的不同结构特征，将讲台上的12个几何体进行分类，并说明每一类具有怎样的结构特征.

学生以小组为单位进行讨论.有学生上台挑选，对几何模型进行了分类，并说明了理由.

生1：第Ⅰ类：(2)(3)(4)(5)(7)(8)(10)(11)(12)；第Ⅱ类：(1)(6)(9)，理由为第Ⅰ类中都有角，第Ⅱ类没有角.

生2：第Ⅰ类：(3)(4)(5)(7)(8)(10)(11)(12)；第Ⅱ类(1)(2)(6)(9)，如图2，理由为第Ⅰ类只由平面构成，第Ⅱ类由平面和曲面构成.

图2

教师将学生的分类结果以及理由书写在黑板上.

师：2位同学视角不一样，分类都非常正确，而且理由充分.书本中的分类与生2一样，所谓英雄所见略同，我们把生2的第Ⅰ类叫做多面体，而且多面体的定义与这位同学给出的理由相吻合.多面体是由若干个平面多边形围成的几何体，围成多面体的各个多边形叫做多面体的面，相邻2个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点.生2将第Ⅱ类的特征总结为由平面与曲面构成，也非常准确，但你有没有发现这类几何体还有一个更加漂亮的结构特征？

生3：这类几何体可以由平面图形旋转而成.

师：请举例说明.

生3：(1)可由长方体旋转而成，(2)可由直角三角形旋转而成，(6)可由半圆旋转而成，(9)可由梯形旋转而成.

师：非常好.根据这类特征，我们将这些几何体取名为旋转体.旋转体是由一个平面图形绕它所在平面内的一条定直线旋转所形成的封闭几何体,定直线叫做旋转体的轴.

教师通过动画演示旋转体的形成过程，让学生加深对旋转体结构特征的印象.

设计意图 通过大量模型与动画演示，让学生形成直观的认识，符合学生从具体到抽象的认知规律.在分类过程中，让学生辨析多面体与旋转体的结构特征，由于标准不同，会出现不同的“正确答案”，因此教师要将所有学生的回答板书于黑板上，并进行肯定，从而激发学生探索的欲望.

1.3 类比分析，探究概念

师：由于时间关系，本课节我们只能研究第Ⅰ类多面体.同学们有没有发现，虽然(3)(4)(5)(7)(8)(10)(11)(12)都属于多面体这个大家族，但是它们各有特点.以小组为单位，模仿刚才多面体、旋转体的分类，对这些多面体再次进行分类，并进行探究.

学生以小组为单位进行讨论，教师进行巡视，最后进行交流.接着学生上台，根据自己的分类，将讲台上的实物模型进行分类.

图3

生4：如图3所示进行分类，第Ⅰ类有平行且全等的2个面，第Ⅱ类不存在平行的2个面，第Ⅲ类有平行的2个面，但是这2个面不全等.

师：很好！在数学上，我们把第Ⅰ类叫做棱柱，第Ⅱ类叫做棱锥，第Ⅲ类叫做棱台.你能根据棱柱的结构特点，对比棱锥、棱台的不同点，给棱柱下个定义吗？

生5：有平行且全等的2个面的几何体叫做棱柱.

师：满足“有平行且全等的2个面”有“资格”叫做棱柱吗？请同学们举例说明.

生6：不能，比如图1中的圆柱.

师：你能进行补充，并给出棱柱的定义吗？

生6：具有平行且全等的2个面、其他面都是平行四边形的几何体叫做棱柱.

图4

师：请大家思考，同时符合这2个条件的几何体有“资格”叫做棱柱吗？请举例说明.

生7：不能！学生上台，将讲台上的2个斜三棱柱(12)拼接在一起，形成了如图4所示的几何体.

学生恍然大悟.

师：你能给出棱柱的定义吗？

生7：具有平行且全等的2个面，其他面都是平行四边形，旁边棱都平行.

师：你们同意生7的说法吗？不同意的请举例说明.

全体学生：同意！

师：我也同意，但是数学概念的叙述讲究简洁美，我认为这些条件中有重复.

生8：“平行四边形”与“旁边棱都平行”重复，平行四边形可以改成四边形.

师：你们同意生8的说法吗？

全体学生：同意！

师：根据同学们的集体智慧，我们得出了棱柱的概念.一般地，有2个面互相平行，其余各面都是四边形，并且每相邻2个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱.棱柱中，2个互相平行的面叫做棱柱的底面，简称底；其余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧面与底面的公共顶点叫做棱柱的顶点.

之后，教师也给出了棱锥、棱台的定义与其相关概念.

设计意图 对于棱柱概念的学习是本节课的重点，也是难点.为了突破难点，体现“生本”课堂，本教学设计从多面体的分类出发，总结概括出棱柱的结构特征，并进一步进行提问“如果你来定义棱柱的概念，你会如何定义”，在定义棱柱概念的过程中，反复筛选能作为棱柱定义的结构特征，学生参与讨论与举例，最终得出棱柱最精简的定义，体现了数学的严谨与简洁美.上述设计步步为营、环环相扣、层层递进，使学生经历完整的数学研究过程，在独立思考与合作交流中不断经历思维的碰撞，获得良好的情感体验，达到一种师生、生生和谐共振的境界.

1.4 拓展延伸，巩固概念

师：虽然这些几何体都从属于棱柱“大家庭”，但是它们性格各异，也具有不同的结构特征.你能再对这些棱柱分类吗？

生9：有的棱柱是直的，有的棱柱是斜的.

师：根据侧棱与底面的位置关系分，侧棱不垂直于底面的棱柱叫做斜棱柱；侧棱垂直于底面的棱柱叫做直棱柱.

生10：侧棱条数不同.

师：侧棱条数不同，取决于底面多边形顶点个数.棱柱的底面可以是三角形、四边形、五边形……我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱……

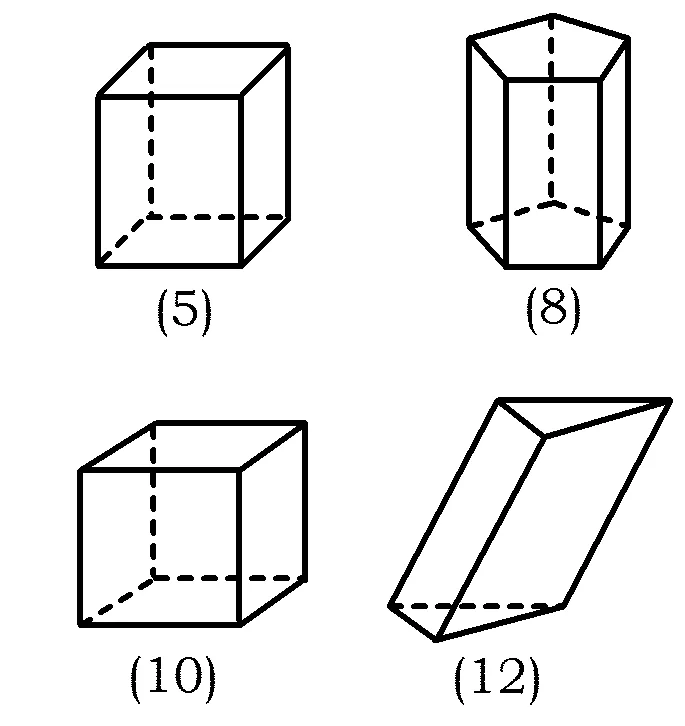
图5

生11：我认为如图5所示的棱柱(5)(8)(10)比(12)看起来舒服，而且更加漂亮.

师：哪里让你看上去比较舒服？

生12：它们是直棱柱，而且底面是正多边形.

师：我们把底面是正多边形的直棱柱，叫做正棱柱.

设计意图 对于不同的棱柱对其结构特征进行再次分类，不仅是对直棱柱、斜棱柱等概念的学习，更是对学习方法的巩固.对学生来说，知识结构、学习能力都是一次很好的提升.

1.5 自谈收获,深化概念

师：请同学们谈谈本节课的收获和感受.

生13：从几何体分类，知道了什么叫做多面体、旋转体、棱柱等，还知道根据不同的特征棱柱也可以分许多类.

生14：我们学的几何体可以从建筑中寻找到雏形，要当一名建筑师，对几何体的结构特征要非常熟悉.

生15：我发现，我们宁波有许多漂亮的建筑，但是平常都没注意到，生活中要做一位有心人.

师：大家总结得很好！上课开始阶段，欣赏并领略了宁波的建筑之美，本节课接近尾声之时，我们一起欣赏世界上的建筑之美，进一步体会数学之美.

教师PPT播放世界上有名的建筑：北京鸟巢体育馆、巴黎罗浮宫、北京水立方、印度卵形大厦、英国塔桥、阿拉伯酒店、纽约双子塔、印度泰姬陵……

2 课后感悟

2.1 以生为本是教学设计的根本

《数学课程标准》指出：“学生的数学活动不应只限于对概念、结论和技能的记忆、模仿和接受，独立思考、自主探究、动手实践、合作交流、阅读自学等都是学习数学的重要方式.”“空间几何体的结构”作为一堂概念课，如果只靠教师在讲台上讲解和演示，学生对空间几何体的印象显然不会深刻，也很难激起探究的兴趣.笔者通过引导学生根据几何体的不同特征，对12个几何体模型按照不同的分类标准进行不断地分类，达到全生参与、全程参与的效果，加深了学生对各种几何体概念的辨析.

皮亚杰认为：“学生的思维还处于由具体形象思维向抽象逻辑思维过渡的阶段，还处在具体运算阶段，这个时期的学生思维虽已能抽象概括并进行简单推理，但整个过程还是不能离开具体事物进行.”作为立体几何的起始课，简单的空间几何体可看作学生学习立体几何的“启蒙老师”，因此课程设计要力求起点低，笔者通过PPT、几何体模型、动画演示让学生直观地感知结构特征，问题设置有梯度，如本节课设计了一系列的问题串和追问：“你能根据棱柱的结构特点，对比与棱锥、棱台的不同点，给棱柱下个定义吗？”“满足有‘平行且全等的2个面’有‘资格’叫做棱柱吗？请同学们举例说明.”“你能进行补充，并给出棱柱的定义吗？”等等，使学生跳一跳就能够得着，符合学生的认知规律.

2.2 教学中要重视学法指导的渗透

授人以鱼不如授人以渔，教育的重点在于学习方法的传授，而不仅仅是书面知识的灌输.“空间几何体的结构”作为章节起始课，是在学生已对空间几何体有了感性认识的基础上，让学生根据几何体不同的结构特征，归纳出多面体、旋转体、棱柱等

定义，对几何体建构起理性的认识，同时为后面分析点、线、面的位置关系作好准备，起到承上启下的作用.本节课的重点不是介绍棱柱、棱锥等几个相关概念，而是让学生经历对学习对象进行观察、归纳、分析、概括、辨析的思维过程和认识数学新对象的基本方法.在笔者的引导下，学生先是学习了多面体与旋转体的相关概念，体会了认识一个新的数学概念的“基本套路”，然后教师下达任务：学生类比多面体与旋转体的学习，自主探究棱柱等几何体的结构特征与相关概念.这种类比的思维贯穿课堂始终，引领全局，一气呵成，构成了整堂课的主线[1].

2.3 课堂教学中让学生感受数学之美

笔者在教学过程中，时时引领学生欣赏数学美.比如“几何体的美在于它有美的结构特征”，这是数学的对称美；比如在得出棱柱概念时，有学生说“具有平行且全等的2个面，其他面都是平行四边形，旁边棱都平行”可以成为棱柱的定义，但是笔者提出数学概念力求简洁，引导学生去掉重复的条件，让学生欣赏数学的简洁美.《数学课程标准》指出：“教学中应引导学生初步了解数学科学与人类社会发展之间的相互作用，体会数学的科学价值、应用价值、人文价值”[2].

笔者从哈尔莫斯的名言开始本节课，设置悬念，以宁波的著名建筑物创设情境，并介绍这些建筑物的地址、历史，使得本土文化在数学课堂上传播，也使学生懂得数学来源于生活、用于生活，鼓励学生做生活的有心人，发现身边的数学美.结尾处播放著名建筑物，鼓励学生学好数学，以后能够在建筑行业大展身手.

[1] 叶琪飞．渗透学法，让学生的思维枝繁叶茂[J]．中学数学，2015(7)：11-12．

[2] 中华人民共和国教育部.普通高中数学课程标准(实验)[M]．北京：人民教育出版社，2003.

2017-02-15；

2017-03-16

张 磊(1987-)，男，浙江宁波人，中学一级教师.研究方向：数学教育.

O123.2

A

1003-6407(2017)06-14-04