一道数列放缩题解法改进的心路历程*

●陈寒极 (慈溪中学 浙江慈溪 315300)



一道数列放缩题解法改进的心路历程*

●陈寒极 (慈溪中学 浙江慈溪 315300)

高三复习阶段，随着学生学习水平的提高，以及个人知识发展的差异，对同一个问题会有不同的解法，但是解法会有优劣，思考入手点也会有难易的差别，比如数列放缩题就是一个极好的例子.文章通过一题多解，提炼方法后化为多题一解，并归纳解题步骤以及解题中的注意点，从而有效地解决这类问题.

数列；放缩；等比；改进

在高三一轮复习中，有这样一个问题：

例1[1]已知数列{an}的前n项和Tn满足an+1=2Tn+6，且a1=6.

(浙江省台州中学2016届高三第1学期期中考试优化卷)

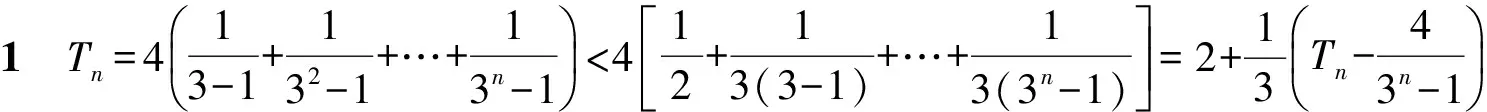
从而

于是

故

Tn<3.

所以

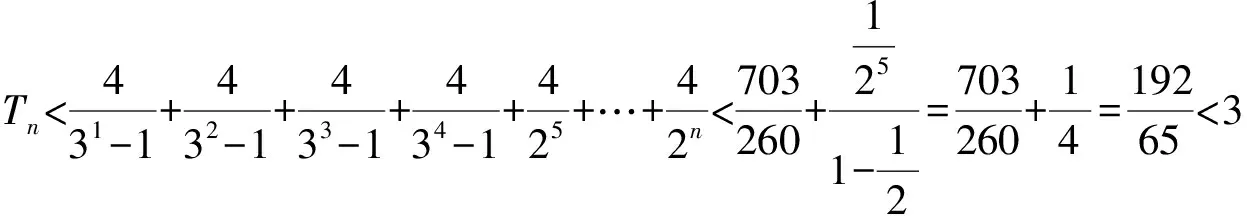
(注：留出4项不变，从第5项开始放缩.)

(注：留出3项不变，从第4项开始放缩.)

(注：使用糖水不等式需要注意分母大于分子.)

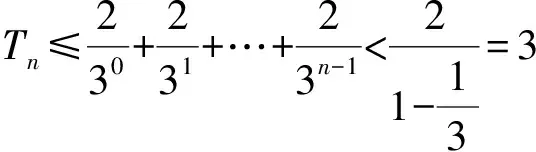
评析 总结这6种方法：方法1类似于等比数列前n项和公式的推导方法,是神来之笔；方法2凑出一个拆项表达式然后求和；方法3～6都在努力放缩为一个等比数列，然后化为无穷递缩等比数列求和，其中方法3需留出4项，方法4需留出3项，方法5需留出1项，而方法6不用留项，是相对而言最好的放缩.

在感叹于学生创造力的同时，笔者又在思考怎么放缩才能相对便捷地求出结果，同时方便学生理解和掌握呢？无独有偶，在练习中又碰到以下问题.

(2015年浙江省镇海中学数学模拟试题)

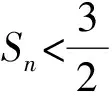
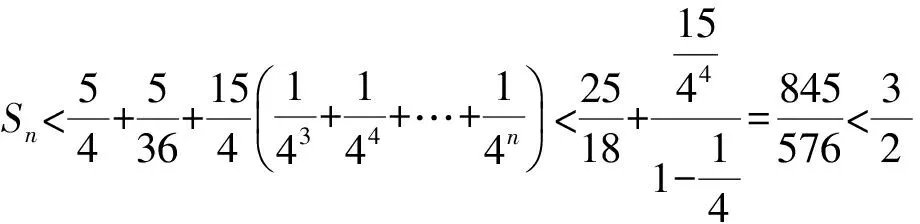
(注：留出2项不变，从第3项开始放缩.)

(注：留出2项不变，从第3项开始放缩.)

(注：留出2项不变，从第3项开始放缩.)

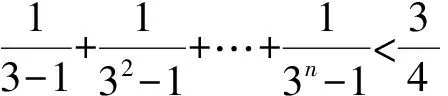
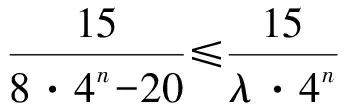
从而

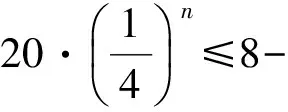
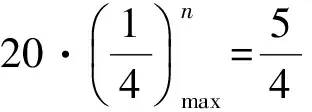
下面给出几个练习题，说明该方法是有效的、方便的.

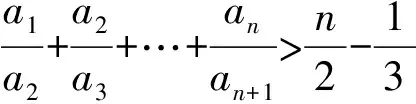
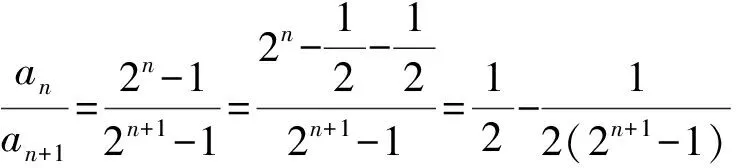
即证

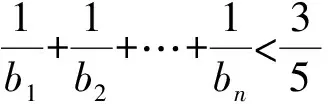
本题的另一种证法如下：

当n为偶数时,

再留出第1项和第2项，求和得出证明.

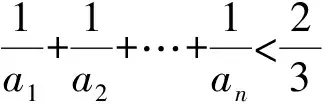
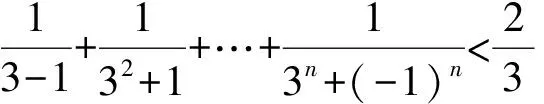
[1] 曲一线.浙江38套模拟卷汇编[M].北京：教育科学出版社，2016.

[2] 王献新.全品高考复习方案2017一轮复习用书教师手册[M].北京：北京教育出版社，2016.

2017-02-15；

2017-03-16

陈寒极(1980-)，男，浙江慈溪人，中学一级教师.研究方向：数学教育.

O122.3

A

1003-6407(2017)06-26-04