立足思维起点指向思维深刻

凌佳

一、习题背景分析

数学知识的巩固、内化、拓展离不开必要的练习。设计练习题时应摒弃机械的“题海战术”，更应注重练习本身的开放性、科学性、挑战性和思维含量。好的练习作为一堂课好的学习材料，不仅应该具有起点低、开放度大等特点，而且要保证人人都能参与，能在同一个问题情境中使不同水平的学生有不同的获得，而且学生能够通过练习探寻有价值的数学任务，渗透转化思想，发展学生合情推理能力和创新思维能力。基于以上的思考，笔者设计了以下几组习题。

二、习题设计

（一）习题呈现（第一题组）

先目测，哪个长方形的周长长？哪个长方形的面积大？

如果A长10厘米，宽4厘米，B长7厘米，宽6厘米。

先猜一猜，哪个长方形的周长长？哪个面积大？再算一算，哪个的周长长？哪个的面积大？

【练习目标】

1.引导学生从已有的知识和经验中，交流发现的规律。

2.引导学生辩析“一个长方形，如果周长比较长，那么面积就比较大”，这样的说法对不对？并说明理由。

3.组织小组合作学习，通过自己的方法证明这个结论的对与错。

【设计意图】练习设计需从学生的学习起点出发，本组练习学生的学习起点是周长和面积的概念及计算方法，这是学生都有的知识基础，让每个学生都能融入课堂积极地思考问题。顺着学生原有的认知，发现在条件改变后学生产生的困惑点和易错点，通过辩析、小组合作等学习方式，牢牢抓住学生的思维起点，感悟周长较长的长方形面积不一定大。

（二）习题呈现（第二题组）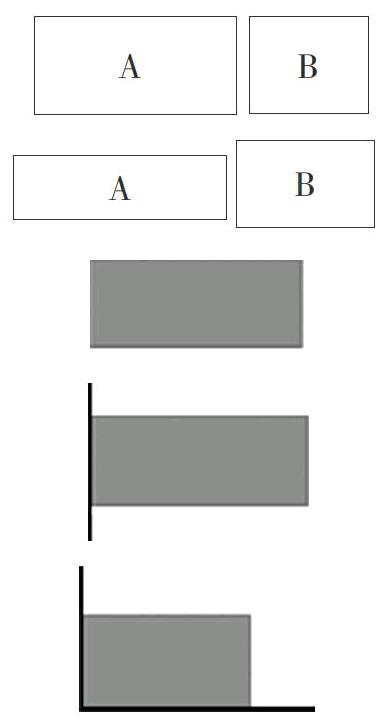

1. 用一条长24米的篱笆围出一个长方形花园。要围出尽可能大的花园，长和宽分别可能是多少？面积是多少？

2. 用一条长24米的篱笆围出一个长方形花园。如果一面靠墙，要围出尽可能大的花园，长和宽分别是多少？面积是多少？

3 用一条长24米的篱笆围出一个长方形花园。如果两面靠墙，要围出尽可能大的花园，长和宽分别是多少？面积是多少？

【练习目标】

1.基于第一题组可以得出结论：周长长的长方形，面积不一定大。通过追问“如果周长一定，那么什么情况下面积最大呢？”引发学生思考。

2.巩固双基，建立知识结构，发展学生思维，提高学生的推理能力和解决问题的能力，加强对概念的理解。

【设计意图】本习题设计从不靠墙，到一面靠墙，再到两面靠墙，将同一问题情境分成三种不同情况让学生经历解决问题的过程。尤其是当一面靠墙的时候，学生会迁移不靠墙的经验，觉得长和宽最接近的时候面积最大，而事实并非如此。因为不靠墙是“长和宽之和一定”的情况，而一面靠墙是“长和两倍宽之和一定”的情况，与之前的结论相矛盾，既而引发学生重新思考问题。好的数学问题不仅不会让学生形成思维定势，还会激发学生思维火花的迸发。当两面靠墙时，因为有了之前的思考作为铺垫，绝大多数学生不难在对比和感悟中找寻到问题解决的策略，从而灵活地应对不同情况下的问题。本组习题不仅给了后进生巩固基础知识的机会，而且训练了优等生的数学思维，让不同水平的学生有不同的获得。

（三）习题呈现（第三题组）

1.一张长30厘米、宽20厘米的长方形纸，周长和面积分别是多少？一次对折后，猜想周长和面积各是多少？再验证你的猜想。（计算验证）

猜想：周长=50厘米 面积=300平方厘米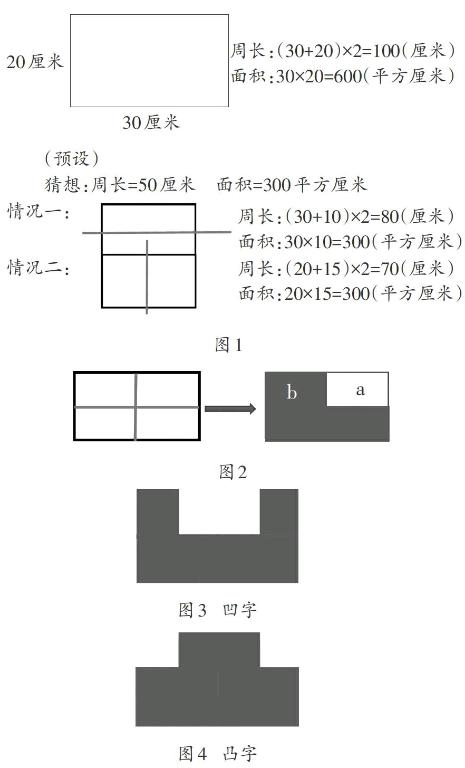

2.再一次对折后变成图2中的a（空白部分），猜想一下它的面積是多少。思考你是怎么验证你的想法的？展开后将a（空白部分）剪去，变成了图2中的b（黑色部分），b的周长和面积各是多少？

【练习目标】

1.动手操作，初步感受长方形经过对折之后，周长和面积发生了怎样的变化。

2.在动手操作中感受数学的魅力，体验成功的喜悦，从而帮助学生建立自信，培养学生从几何直观到抽象思维的过渡，再一次调动学生参与课堂教学的积极性。

【设计意图】本组习题让学生先经过大胆猜想，然后动手操作，再通过自己的实践直观感受到长方形的周长和面积发生着怎么样的变化，从而验证自己的猜想。借助学生画的直观图，帮助学生理清求图形b的周长可以转化为求原长方形的周长，有机渗透转化思想，促进学生求异创新思维能力的发展。教师应该多创设对学生具有思考价值的问题、能激发其自主学习的有探究性的数学任务，这样，我们的课堂才会更有数学味。

（四）习题呈现（第四题组）

1.把图2中的a（空白部分）往里推，变成图3的形状，它的周长和面积又是多少呢？

2.如果把凹进去的部分往上翻，变成图4的形状，它的周长和面积又是多少呢？

【练习目标】

1.提炼总结，帮助学生完成知识建模，其他学生补充、交流，同时学会总结回顾知识的方法。

2.在学习知识的同时，培养学生学会总结的能力。

【设计意图】将不规则图形变成“凹”和“凸”两个形状的图形（电脑动态演示）。先引导学生对话“凹”和“凸”，“凸”对“凹”得意地大笑：“我不仅面积比你大，而且周长比你长。”让学生扮演“凹”进行反驳。学生根据表面观察，容易产生“凸”的周长比“凹”的周长长的认识偏差，通过相互辩驳，使学生明晰道理，将学生思维引向深入。通过计算，再次打破了学生原有的“周长越长的图形面积越大，面积越大的图形周长也越长”的思维定势。在此基础上，引导学生抽象、概括并总结出“周长相等的图形面积不一定相等，面积相等的图形周长不一定相等”的结论，从而揭示数学规律。在对比、体验和感悟过程中，不仅提升了学生的理性思维，也有效培养了学生思维的深刻性。

三、設计感悟反思

数学习题教学，不仅要尊重数学知识本身，更要重视对学生数学思维能力的培养。这样才能使学生拥有一双用数学视角观察世界的眼睛，拥有一个能进行数学思维的头脑，拥有一种能用数学方法解决问题的能力，才能把数学的根留住，让学生真正拥有智慧。这四组习题将教学的着力点放在发展学生的合情推理能力、创新思维能力上，重视实践探索，引导猜想验证，启迪学生思考，教给思考方法。

（一）引导猜想验证，发展合情推理能力

猜想是一种合情推理能力，属于综合性的认知过程。学生在“猜想—验证”的问题探索过程中，能亲身经历用合情推理发现结论的推理过程，在探索过程中感悟数学思想，积累数学活动经验。解答习题中引导学生将长方形纸对折，有的左右方向对折，有的上下方向对折，打开都变成两个小长方形。然后学生猜想对折后每个小长方形的周长和面积各多少。最后计算验证自己的猜想。接着又经历第二次对折，让学生猜想连续对折两次后这个小长方形的面积，要求学生想想怎么验证自己的猜想，并鼓励学生用多种方法验证自己的猜想。学生先经过大胆猜想，然后动手操作，从实践中直观感受长方形的周长和面积发生着怎样的变化，让学生通过计算验证自己的猜想，既发展了学生的合情推理能力，也让学生在实践探索中感受到数学的魅力，体验到成功的喜悦。

（二）寻求多种策略，发展创新思维能力

创新离不开思维，没有思维就不可能有创新。本习题在设计时并不满足学生已有的思维成果，而是引导学生从不同角度思考和探索，进行创造性的解决问题。先将长方形按左右、上下连续对折两次后展开，再减去右上角的四分之一的小长方形，然后将剪去的空白部分往里推变成“凹”，最后将凹进去的部分往上翻变成“凸”。学生在计算每个不规则图形的面积时，并不拘泥于狭隘的解题思路，突破单一的思维模式，敢于打破常规，转换角度进行思考，沿着不同方向，对同一问题从多角度加以解决，学生的创新思维能力得到有效培养。

（三）组织比较辨析，发展思维的深刻性

组织比较辨析，有利于让学生的思维在比较、辨析中走向深刻，进而发展学生思维的深刻性。数学中经常用到的数形结合既是一种重要的数学思想，又是一种获取知识和解决问题的有效方法。习题利用数形结合的方式，引导学生从形的方面去研究，进行形象思维；从数的方面去分析，进行抽象思维。对各种图形进行有序排列整理，在对比、体验和感悟中让学生体会各种图形周长和面积的变化规律，感悟变与不变的数学思想，提升了学生的理性思维。

本习题设计以发展学生的思维能力为主线，通过一张长方形纸的不断变化，在变化中求深刻。让学生在实践中体验，在体验中思考，在思考中感悟，在感悟中创造，使学生的思维能力得以提升。

（浙江省湖州市织里实验小学教育集团 313008）