深基坑土钉支护结构的稳定性分析及三维有限元数值模拟

何 渊，廖 瑛

（苏州科技大学 土木工程学院，江苏 苏州215011）

深基坑土钉支护结构的稳定性分析及三维有限元数值模拟

何 渊，廖 瑛

（苏州科技大学 土木工程学院，江苏 苏州215011）

对土钉支护结构在各种破坏形式下的稳定性进行了分析及有限元数值模拟。研究了模糊随机可靠度的计算方法，并结合工程实例，通过编写MATLAB程序计算得到模糊可靠指标，并与安全系数、传统可靠指标相比较，得出了相关结论。在此基础上采用ABAQUS有限元软件建立了土钉支护结构的三维有限元模型，分析了基坑变形与土钉轴力的变化规律。研究表明：土钉支护结构能够有效地限制土体变形，故设计与排布土钉非常关键。

基坑；稳定性；土钉支护；MATLAB；模糊随机可靠度；ABAQUS

随着土木工程建设的快速发展，高层、超高层建筑越来越多，导致基坑越来越深，尺寸越来越大，对于基坑工程中支护结构稳定性的要求也越来越高。

土钉支护结构[1-2]是目前在我国广泛应用的基坑支护形式之一，具有成本低、施工简单、操作方便及安全可靠等优点。而基坑土钉支护结构的稳定可靠性分析是根据土体及支护结构可能发生的不同破坏形式，建立极限平衡方程并进行概率计算。在目前的基坑支护结构设计方法中，安全系数法[3]没有考虑基坑工程中的不确定性因素；传统的可靠度分析方法[4-5]只考虑了不确定性因素中的随机性特点；而模糊随机可靠度法[6]更合理、科学地将随机性与模糊性同时考虑进去，使得计算结果更全面、更科学。

文中首先在建立基坑土钉支护结构于各种破坏形式下的极限状态函数的基础之上，然后运用工程计算软件MATLAB和大型有限元软件ABAQUS[7]，对经典支护结构工程实例进行了模糊随机可靠性分析及数值模拟，实现了对基坑土钉支护结构真实工作状态的反映。

1 结构的模糊随机可靠度

1.1 传统的结构可靠度

结构可靠度定义为结构在规定的时间内，完成预定的功能的概率，在结构可靠度分析中，是通过其功能函数来反映结构的极限状态，通常设结构的稳定可靠性功能函数为Z=R-S，其中R表示结构抗力、S表示荷载效应。并规定Z＜0时，结构失效；Z=0时，结构处于临界极限状态；Z＞0时，结构可靠。当随机参数不服从正态分布时，一般可采用JC法、实用分析法、映射变换法等将其转换成当量正态分布变量，并将非线性功能函数展开成Taylor级数（取至一次项），然后再通过迭代来计算求解可靠指标及验算点的坐标，进而计算结构的失效概率。

1.2 结构的模糊随机可靠度

以及结构的模糊可靠指标可表示为

与非正态随机变量的当量正态化方法相对应，如果将隶属函数的补函数视为一个新的随机变量Xn+1的概率分布函数FXn+1（xn+1），即则

式（1）可化为

其中

式（5）中，I（ze）为经典可靠度理论中的示性函数，而式（6）为模糊事件可靠度分析的等效功能函数，可将其作为结构功能函数，应用经典可靠度的分析方法可求得模糊事件的可靠指标。

2 土钉支护结构稳定性分析

在土钉本身设计强度满足的情况下，基坑土钉支护结构的稳定性验算应包括:整体抗滑移验算、整体抗倾覆验算、抗深层挤滑破坏验算、土钉整体抗拔验算、抗楔体滑落验算以及单根土钉抗拔验算等[9]。

2.1 整体抗滑极限状态函数及中值安全系数

如图1所示，土钉墙受墙后主动土压力Ea、墙体自重W及墙顶均布荷载q的作用，其中Ea的水平分力Eax为滑动力，由W及q引起的摩擦力Ff为抗滑力。

在可靠度分析中，若将黏聚力c、内摩擦角φ视为随机变量，Eax即为荷载效应函数S，Ff为抗力函数R，则建立整体抗滑极限状态函数和中值安全系数为

式中，γ、φ、c分别为土重度、内摩擦角及黏聚力；q、H分别为墙顶均布荷载及土钉墙高度；Ka=tan2（45°-φ/2），其为主动土压力系数；B=11L/12，其为土钉墙厚度（当土钉倾斜时，B=11Lcosα/12，α表示土钉与水平面间的夹角）。

2.2 整体抗倾覆极限状态函数及中值安全系数

如图2所示，墙后主动土压力的水平分力Eax构成倾覆力矩Me中的作用力，作用点位于土压力分布图形心处。土体自重W与墙顶均布荷载q的合力构成抗倾覆力矩Mw中的作用力，因为q远小于W，故力的作用点约位于墙的中心处，即1/2土钉墙厚度处。

Mw即为抗力函数R，Me为荷载效应函数S，从而可建立整体抗倾覆极限状态函数和中值安全系数为

2.3 抗楔体滑落破坏极限状态函数及中值安全系数

如图3所示，破裂面左侧土体作为楔体单元进行受力分析，沿边坡纵向长度取Sx（即土钉水平间距）。建立抗楔体滑落破坏极限状态函数和中值安全系数为

图1 抗滑受力简图

图2 抗倾覆破坏受力简图

图3 抗楔体滑落受力简图

式中，hi为第i根土钉到坡顶的距离，Li为第i根土钉的长度。

2.4 土钉整体抗拔出极限状态函数和中值安全系数

土钉的抗拔力即为土钉所提供的界面摩阻力的合力T，拔出力为潜在滑裂面后的土压力Ea。将黏聚力c、内摩擦角φ、界面粘接强度τ视为随机变量，则建立土钉整体抗拔出破坏极限状态函数和中值安全系数

式中，地面超载合力Q=0.3HSxq；土体重力G=0.262 5γH2Sx；α=arctan（0.25H/0.3H）=39.81°，其为滑裂面底部与水平线夹角；θ为土钉与水平面的夹角；Sx为土钉横向间距；n为土钉总排数；m为土钉与破裂面的交点在破裂面拐点上方的土钉排数；Ti=πDτLeicosθ，它是第i根土钉锚固力，D为土钉钻孔直径，τ为土钉体的界面黏结强度，Lei为第i排土钉锚固长度（潜在滑裂面后的土钉长度），由式（13）的分段函数确定

式中，me为工作条件因素，对于临时工程，me=1.1，对于永久工程，me=1.2；土压力系数k=（k0+ka）/2，其中k0为静止土压力的系数，k0=1-sinφ；ka为主动土压力的系数，ka=tan2（45°-φ/2）。

2.5 土钉单根抗拔出极限状态函数和中值安全系数

设第i根土钉锚固力为Ti，第i根土钉支撑范围内面层上的土压力为Ei，则土钉单根抗拔出破坏极限状态函数和中值安全系数为

式中，Ti=πDτLeicosθ；Ei可根据文献[9]中式（5-22）确定。

3 工程实例

3.1 工程概况

某基坑工程[10]各土层的物理力学参数见表1。该工程开挖深度约8 m，采用土钉支护结构。根据设计要求，土钉支护坡高8.0 m，共设置5排土钉，长度为6.0 m，倾角10°，土钉的首排埋深、水平间距、垂直间距均为1.2 m，钻孔直径0.15 m。

表1 土层参数表

3.2 选取参数

为简化计算，将该场地土层视为均质土层，其物理力学指标采用对土层厚度的加权平均值，见表2。

表2 土层计算参数表

对于隶属函数可按如式（18）所示的降半梯形分布来选取

对其模糊过渡区的上限和下限一般可根据基坑类型、实践经验和设计要求等来确定[11]，b=0.2μs、a=-0.1μs。

3.3 计算结果及结果分析

根据安全系数法、结构可靠度理论法和模糊随机可靠度法，并使用Matlab数值软件来编程计算该土钉墙整体抗滑移、整体抗倾覆、土钉整体抗拔、土钉单根抗拔以及抗楔体滑落的稳定性，相应计算结果如表3所示。

表3 土钉墙各稳定验算模式计算结果

由表3可知，抗倾覆中值安全系数K＞1.5，其他各安全系数K＞1.3，则此表中的中值安全系数计算结果均满足稳定性验算要求。由于深基坑开挖支护的土钉支护结构是一种临时结构，只需其在1～2 y内不失效即可，从而可根据美国LRFD规范对于临时建筑将目标可靠指标取为β0=2.5。在整体稳定性的验算结果中，以土钉整体抗拔的可靠度最小，其模糊可靠指标β=2.576 1＞2.5，则能判断该结构整体的稳定性设计满足要求，且设计较为保守。在单根土钉抗拔出验算中，除第四排模糊可靠度外β=2.405 1＜2.5，其余各排均满足要求。考虑到土钉是依靠群体起作用的，可允许个别土钉值β略小于β0，故该土钉支护结构达到安全设计要求。

此外，相对于其他的失稳破坏模式，土钉整体抗拔的可靠指标和模糊可靠指标皆为最小，故在该土钉支护结构的失稳模式中，可认为土钉整体抗拔失稳处于关键地位，图4、图5及图6分别给出了基于c、φ、τ不同概率分布类型的土钉整体抗拔的可靠指标与模糊可靠指标随土钉长度变化的对比曲线图。

由图4～6可知，基于随机变量不同的概率分布类型，可靠指标、模糊可靠指标随土钉长度的增加均呈近似线性增长趋势；此外，黏聚力c、内摩擦角φ的概率分布类型对可靠指标、模糊可靠指标的影响不大，而界面粘结强度τ的概率分布类型对可靠指标、模糊可靠指标的影响较大；且当土钉长度相同时，若τ服从极值型分布的可靠指标，则模糊可靠指标最大，但τ服从正态分布的可靠指标，模糊可靠指标就最小。

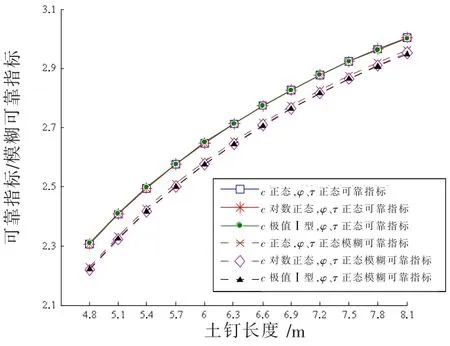
图4 c不同概率分布时β/β随土钉长度变化

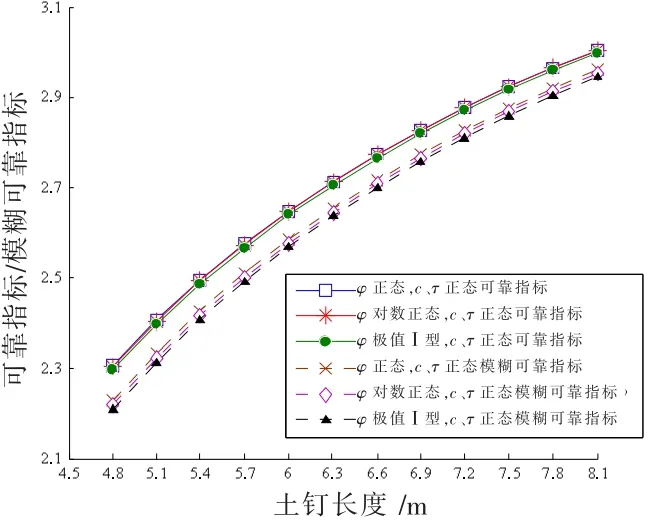
图5 φ不同概率分布时β/β变化

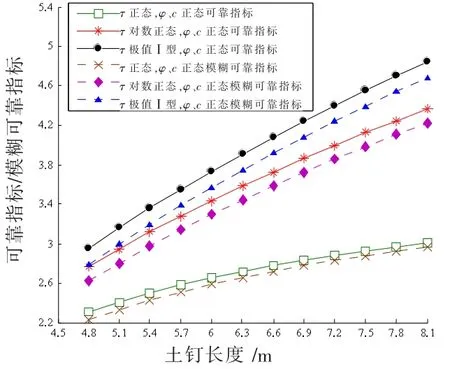
图6 τ不同概率分布时β/β变化

由于c、φ的概率分布类型对结果的影响不明显，故以下的分析中都假设c、φ、τ均服从正态分布，以此来研究各个参数对可靠指标、模糊可靠指标的影响。图7～10是基于随机变量均服从正态分布的土钉整体抗拔稳定性可靠指标、模糊可靠指标随随机变量均值及变异系数的变化对比图。

由图7～9表明，随着c均值、φ均值及τ均值的增大，可靠指标、模糊可靠指标均呈增长趋势，但前两者近似呈线性变化，而后者近似呈抛物线型变化；此外，从可靠指标、模糊可靠指标的变化区间可见，c的均值对可靠指标、模糊可靠指标的影响最大，τ的均值对可靠指标、模糊可靠指标的影响最小，这都体现出了基坑工程稳定性问题的复杂性。

由图10可见，与均值截然不同的是，随着变异系数δc、δφ和δτ的增大，可靠指标、模糊可靠指标均呈下降趋势，但下降的幅度不同，其中前两者下降的幅度较为平缓且曲线近似线性，而第三者下降的幅度最大、呈抛物线型下降，表明δτ对可靠指标、模糊可靠指标的影响较大，同样体现了基坑工程稳定性问题的复杂性。

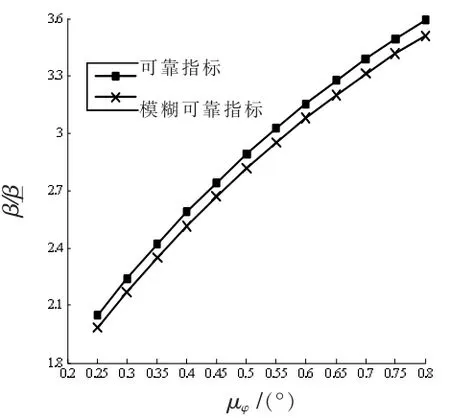
图7 β/β随μφ变化对比图

图8 β/β随μc变化对比图

图9 β/β随μτ变化对比图

图10 β/β随δ变化对比图

4 土钉支护的有限元数值模拟

4.1 工程概况

根据以上工程实例，设计有限元计算模型和计算区域的几何尺寸，基坑开挖深度、土钉尺寸、土钉放置布局如图11～12所示。边坡土体采用均质土体，没有放坡，喷射混凝土面层厚度为0.2 m。为了能达到真实反映深基坑工程中应力变形的目的，必须考虑深基坑开挖过程中的非线性与逐次性[12]，因为把开挖过程当作是一次性完成并以此来计算分析应力变形的方法不会产生太好的结果。文中模拟每步土钉支护施工的过程为开挖一层一定深度的土体，设置一排土钉再喷射混凝土面层，并将被开挖土体单元的等效结点力反向施加于开挖面上，使开挖面的应力等于零。

图11 模型几何尺寸图（单位：m）

图12 土钉墙体立面图（单位：m）

由于文中主要探讨基坑的稳定性分析，为了简化计算，分析中土体采用理想线弹塑性Mohr-Coulomb模型，土钉为弹性材料，具体的有限元计算参数如表4。

表4 土钉支护的有限元计算参数

4.2 计算结果分析

图13为ABAQUS计算的开挖完成后水平位移图，由图13可见，距离面层越近的土体水平位移越大且向基坑内侧移动，最大水平位移值为39.62 mm，处于第四排土钉与坑底之间，这与前人的研究相一致[13-14]；而距离面层越远的土体水平位移越小，达到一定距离后位移趋向于零。在距离土钉加固区以外的土体，最大位移发生在顶部，这与实际相符。图14为基坑分步开挖时基坑水平位移图，可见随着开挖深度越深，基坑水平位移也逐渐增大，这是由于开挖时基坑边坡的侧向约束力逐步解除；但第五步开挖后水平位移的峰值点并不处于深度最深处，而是处于第四排土钉附近。

图13 开挖完成后水平位移等值图

图14 各步开挖后基坑水平位移

图15给出的是基坑开挖完成后的竖直位移图，由图15可知，开挖打破了土体的原始应力平衡状态，使得土体中的应力重新分布；开挖面上的土体都有向下移动的趋势，但由于开挖作业面所受压力较小，使得靠近面层的开挖面土体较远离面层的土体沉降值更大，形成轻微隆起；而随着土体深度的增加，沉降值变小，这与实际相符；对于坡后土体，地表沉降的最大值发生在坡顶附近，且在土钉周围的土体竖直位移比远离土钉的土体竖直位移要小，这是由于土钉有效地限制了土体的竖向变形。图16为基坑分布开挖时基坑竖直沉降量，可知每开挖一步，基坑都会增加一定的沉降量，且每步开挖形成的沉降量分布曲线形状类似，深度越深，沉降量逐渐减少。

图15 开挖完成后竖直位移等值图

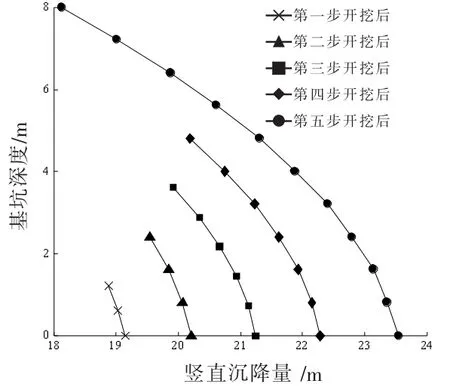
图16 各步开挖后基坑竖直沉降量

图17为基坑开挖后不同位置处的土钉所受轴力分布图，由图17可知，第一排、第二排土钉轴力较小，第四排土钉轴力最大，这与以上Matlab计算软件所求出的土钉单根抗拔出可靠指标、模糊可靠指标相吻合；每排土钉所受的轴力沿土钉延长呈类似的曲线分布，基本呈现出两端小，中间大的抛物线形状，但峰值点不同，深度越深的土钉，最大轴力点位置向靠近面层的方向移动，见图18，它是由基坑开挖完成后各排土钉最大轴力点位置的连线图，该图即为基坑的潜在滑动面。

图19为不同开挖阶段各排土钉最大拉力随基坑深度分布图，从中可知随着开挖深度的加深，各排土钉所受的拉力也随之增大；对于每步开挖后，它上一排的土钉所受最大拉力的增量最大，即表明该排土钉承受的荷载较大，而施工时要确保支护达到一定的承载能力时才能进行下一步开挖。

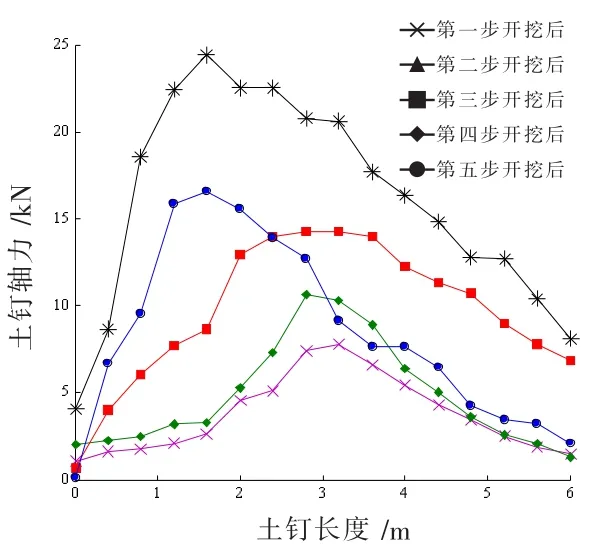
图17 开挖完成后各排土钉轴力分布

图18 最大轴力点位置连线（潜在滑裂面）

图19 各排土钉最大拉力分布

5 结论

通过对一基坑土钉支护结构进行稳定性分析及数值模拟，得出如下结论：

（1）从工程实例中可知，各项中值安全系数均满足要求，而个别可靠指标、模糊可靠指标出现不满足或偏小的现象；且中值安全系数与可靠指标、模糊可靠指标不具有类比性，这是由于可靠度计算中变异系数起作用的结果，从而说明了中值安全系数法的不足。

（2）模糊可靠指标均小于可靠指标，这是由于模糊随机可靠度法较传统的可靠度法额外地考虑了参数的模糊性特点，而考虑更多不确定性因素会增大结构失稳的概率，故模糊随机可靠度理论更为科学而系统。

（3）对于基坑土钉支护结构，土钉的长度增加能够加大结构的安全性能；在可靠度、模糊可靠度计算中，合理确定随机变量的概率分布类型、均值及变异系数极其重要。

（4）对于同一水平面的坡后土体，靠近土钉的土体水平位移与竖直位移较小，而远离土钉的土体水平位移与竖直位移较大，这说明了土钉对基坑稳定性的影响较大，土钉支护结构能够有效地限制土体变形。

（5）每排土钉所受的最大轴力位置即为土体变形最大位置，且各排土钉轴力最大点的连线，就是边坡最小安全系数的滑动面，即基坑的潜在滑动面，故应注重此区域的支护和勘察检测工作。

[1]杨光华.深基坑支护结构的实用计算方法及其应用[M].北京：地质出版社，2004.

[2]孔德森，吴燕开.基坑支护工程[M].北京：冶金工业出版社，2012.

[3]中华人民共和国住房和城乡建设部.JGJ120-2012建筑基坑支护技术规范[S].北京：中国建筑工业出版社，2012.

[4]李清富，高建磊，乐金朝，等.工程结构可靠性原理[M].郑州：黄河水利出版社，1999.

[5]贡金鑫，魏巍巍.工程结构可靠性设计原理[M].北京：机械工业出版社，2007.

[6]张明.结构可靠度分析——方法与程序[M].北京：科学出版社，2009.

[7]费康，张建伟.ABAQUS在岩土工程中的应用[M].北京：中国水利水电出版社，2013.

[8]贡金鑫.工程结构可靠度计算方法[M].大连：大连理工大学出版社，2003.

[9]黄安全，王安明，毕理毅，等.深基坑支护工程可靠度分析与数值模拟[M].郑州：黄河水利出版社，2009.

[10]姚海慧，陈晓霞，付向红.深基坑土钉支护抗楔体滑落可靠度分析[J].河南科技大学学报（自然科学版），2013，34（2）：66-69.

[11]廖瑛，王月香.基于模糊随机变量不同概率分布的基坑稳定性分析[J].四川建筑科学研究，2013，38（6）：142-144.

[12]武亚军，栾茂田，杨敏.深基坑土钉支护的弹塑性数值模拟[J].岩石力学与工程学报，2005，24（9）：1549-1554. [13]李彦初，陈轮.深基坑复合土钉支护的三维有限元数值分析[J].工程勘察，2012，40（2）：11-15.

[14]杜飞，陈志龙.软土地层中基坑复合土钉支护的变形性能分析[J].清华大学学报（自然科学版），2000，（S1）:87-90.

Stability analysis of the soil nailing structure for deep foundation pits and three-dimensional finite element numerical simulation

HE Yuan,LIAO Ying
（School of Civil Engineering,SUTS,Suzhou 215011,China）

The stability of the soil nailing structure under various forms of damage is analyzed and the finite element numerical simulation is carried out.This paper studies the calculation method of the fuzzy-random reliability,and obtains the fuzzy reliability index by combining an engineering example with MATLAB programming.The index is compared with the safety factor and the traditional reliability index,and relative conclusion is obtained. On this basis,a three-dimensional finite element model of the soil nailing structure is built by using the ABAQUS finite element software,and the changing rule of the deformation of foundation pit and soil nail axial force is analyzed.The results indicate that the soil nailing structure can limit the soil deformation effectively,thus the design and layouts of soil nails are very critical.

foundation pit;stability;soil nailing;MATLAB;fuzzy-random reliability;ABAQUS

TU473

：A

：2096-3270（2017）02-0006-07

（责任编辑：秦中悦）

2016－07-06

何 渊（1990-），男，江苏丹阳人，硕士研究生。

廖 瑛（1973-），女，副教授，硕士，从事结构理论与计算方法研究，E-mail：liaoying73@sina.com。