远场强震下人字形防屈曲支撑钢框架滞回能需求层间分布规律影响因素分析

徐 华，蒋 明

（苏州科技大学 土木工程学院，江苏 苏州215011）

远场强震下人字形防屈曲支撑钢框架滞回能需求层间分布规律影响因素分析

徐 华，蒋 明

（苏州科技大学 土木工程学院，江苏 苏州215011）

为了将基于能量的设计方法运用到人字形防屈曲支撑钢框架结构中，在远场地震下，利用ABAQUS动力隐式功能，采用不同的地震波对8种人字形防屈曲支撑钢框架结构进行能量分析，研究不同地震波参量和结构参量对人字形防屈曲支撑钢框架滞回能需求层间分布和支撑耗能的影响。研究结果表明：防屈曲支撑滞回耗能占结构总滞回耗能比例均在95%以上；地震动峰值加速度和楼层数对结构滞回能层间分布影响大；强震持时、结构层高和结构跨度对结构滞回能层间分布影响小；结构跨数、结构阻尼比和材料切线模量对结构滞回能层间分布几乎无影响。

人字形防屈曲支撑钢框架；能量平衡；滞回能需求分布；弹塑性时程分析

防屈曲支撑作为一种高效的被动型位移耗能器给钢框架带来了较大的弹性刚度、延性和滞回耗能能力。许多学者研究了防屈曲支撑钢框架结构的抗震性能并与其它支撑结构进行对比。张耀春[1]运用时程法分析了普通、特殊和防屈曲支撑钢框架结构的抗震性能，在罕遇地震下普通、特殊中心支撑钢框架结构的被支撑梁出现部分屈服和失稳，钢支撑在受压时出现大幅面外失稳，防屈曲中心支撑结构的被支撑梁保持弹性，防屈曲支撑在拉压下都屈服耗能。国忠岩[2]对比了普通中心支撑钢框架结构与采用低屈服点钢材的防屈曲中心支撑框架结构的抗震性能，研究结果表明防屈曲支撑钢框架支撑不屈曲，结构位移等响应均小于普通和特殊中心支撑钢框架。贾明明[3]分析了10种不同抗侧刚度比的防屈曲支撑钢框架，比较了防屈曲支撑结构和纯框架结构的抗倒塌能力，在防屈曲支撑结构中支撑与纯框架的抗侧刚度比为6时，结构的地震反应最小，防屈曲支撑可以大幅提高纯框架的抗倒塌能力。近些年，防屈曲支撑钢框架逐渐运用于高烈度区新建建筑中，如北京银泰中心、北京威盛大厦、北京通用时代广场和上海世博中心等。防屈曲支撑钢框架结构在高烈度地区有很好的应用前景。

20世纪50年代Housner[4]提出以弹性伪速度谱来计算结构的弹性输入能，基于能量的抗震思想开始发展。到20世纪80年代，由于震害观测资料和结构实验的积累，人们才意识到能量在反应地震动强度和评判结构的损伤中的重要作用。结构的能量方程可以表述为[5]

式中EK为结构动能，是结构运动惯性力产生的能量；ED为结构阻尼耗能，是阻尼力和每一时间增量步中位移之积；ES为结构弹性应变能；EH为结构结构塑性滞回耗能，是结构内力与塑性位移的乘积；EI为结构总地震输入能量，是底部剪力在地面位移上的乘积。

基于能量的抗震设计方法将地震对结构的作用看作是一种能量的传递、转化和消耗过程，对于防屈曲支撑结构来说，以支撑的轴向拉压变形和框架梁两端塑性铰的形成为代价来消耗地震能量。基于能量抗震设计思想更加注重从结构的损伤模式和耗能机制控制入手[6]，弥补了基于承载力和基于位移的抗震设计方法无法反应出结构累积损伤效应的不足[7-8]。滞回耗能是衡量结构系统抗震性能的重要指标之一。结构的累积损伤与滞回耗能密切相关，结构滞回耗能占结构总耗能的比重可以体现出结构的破坏程度；同时，滞回耗能在结构各构件中的分配情况直接体现出结构是否有具有合理耗能机制。滞回能也被认为是最具工程意义的能量指标[9]。近来，越来越多的学者开始研究以结构滞回能做为损伤指标的能量设计方法，其中一个重要的部分就是结构滞回能的层间分布规律。文献[10-14]研究了远近场地震下抗弯钢框架、人字形中心支撑钢框架、K型偏心支撑钢框架、V型偏心支撑钢框架等结构体系的滞回耗能层间需求分布规律及其影响因素。防屈曲支撑钢框架结构作为一种较新的结构体系，通过运用弹塑性时程分析的方法，分析了地震动和结构因素对人字形防屈曲支撑钢框架结构滞回耗能层间需求分布模式的影响。

1 算例

文中设计的防屈曲支撑钢框架算例代号表示：层数×跨数×层高（m）×跨度（m），文中给出算例10×3× 3.6×7.2、15×3×3.6×7.2和20×3×3.6×7.2的构件截面尺寸（其余算例变动很小），见表1与表2。

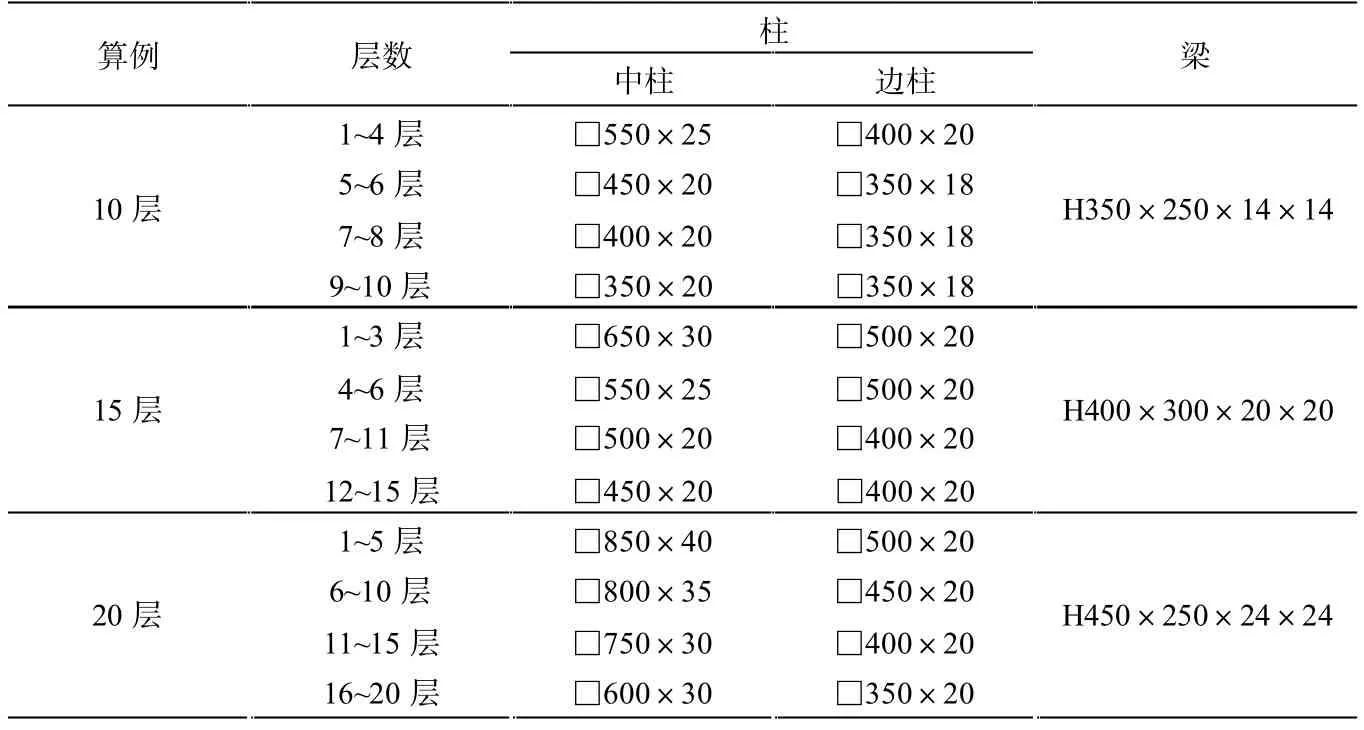
表1 三种结构梁柱截面尺寸 mm

表2 三种结构防屈曲支撑核心截面尺寸 mm

支撑与梁柱节点均铰接，其余节点均刚接，平面图见图1，立面图见图2。设计算例位于8度抗震设防区，设计基本加速度为0.3g；场地为Ⅱ类场地；设计地震分组为第一组；防屈曲支撑内部芯材采用Q235钢，梁柱均采用Q345钢。建模取平面图中2-2轴带支撑的一榀框架，并且假设该榀框架承担该方向上一半的水平地震荷载，不带支撑框架不承受水平地震荷载。计算榀框架竖向荷载取左右相邻跨度各一半的面积，详见图1。

图1 结构平面布置

图2 不同结构立面图

运用ABAQUS/Standard对2-2轴框架进行弹塑性时程分析，防屈曲支撑采用T3D2单元模拟，梁、柱采用考虑剪切变形的B32单元模拟，阻尼采用瑞利阻尼模型。采用双线性随动强化模型作为材料本构关系，其中E1=210 000 MPa，E2=0.01E1，泊松比取为0.3。

参照文献[11]的规定，根据场地条件、场地特征周期、Beta谱在平台段和结构第一周期附近的拟合度，结构在反应谱分析下得出的底部最大地震剪力和在结构多遇地震下弹性时程分析底部最大地震剪力筛选地震波。所有的天然波均来自伯克利地震数据中心,所选自然地震波汇总于表3。

表3 远场自然地震波汇总表

2 滞回能需求层间分布影响因素

2.1 强震持时影响

运用SeismoArif软件拟合了持时分别为40、50、60、70、80、90 s共计18条人工地震波对算例15×3×3.6× 7.2在大震下进行非线性弹塑性时程分析，研究强震持时对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。具体选波数据见表4，其中强震持时定义为Trifuac and Brady持时。相同持时地震波结果取平均值作为最后结果，如图3所示。

表4 强震持时影响所选地震波

图3 强震持时对结构层间滞回能需求分布的影响

由图3（a）可知，随着地震波强震持时的增加，结构总滞回耗能不断增加。从图3（b）中发现，强震持时增加，结构上部的滞回能增加，其中8到13层最为明显，下部滞回耗能减小，集中表现在2到5层。最大幅度差0.031出现在结构第3层，为该层最大滞回能比例的17.6%。从图3(c)可见，结构中防屈曲支撑耗能占结构总滞回耗能的比例在不同强震持时的地震波作用下保持在99%以上，防屈曲支撑几乎承担了所有的塑性耗能，框架部分基本保持在弹性范围内。

2.2 结构阻尼比影响

采用瑞利阻尼来研究阻尼比对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。钢结构阻尼比一般在2%到5%之间，为了研究结构阻尼比的影响，本节选取2%、3.5%、5%三种情况，在罕遇地震下对算例15×3×3.6×7.2进行弹塑性时程分析，所选波见表5，结果见图4。

表5 考虑阻尼比对结构影响所选用的地震波

图4 结构阻尼比对结构层间滞回能需求分布的影响

从图4（b）中可以看出，随着结构阻尼比的增加，结构下部的滞回能逐渐增加，增大幅度最大处出现在结构第3层，幅度差为0.01，为该层最大滞回能比例的7%，上部滞回能曲线几乎重合，可见阻尼影响较小，可以忽略。图4（a）中Et为结构总耗能，Eh为结构滞回耗能，结构阻尼对结构总耗能几乎无影响，但对结构滞回耗能在结构总耗能中所占的比例影响很大，结构阻尼比在5%时，阻尼耗能达到了51%；结构阻尼比在2%时，阻尼耗能只占了总耗能的32%。图4（c）中支撑总滞回耗能占结构总滞回耗能比例在不同阻尼的情况下几乎都保持在96%以上。

2.3 跨度影响

采用算例15×3×3.6×7.2、15×3×3.6×7.5和15×3×3.6×7.8来研究跨度对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。分别对三种结构在大震下（510 gal）进行弹塑性时程分析，计算结果取平均值，结果见图5。

由图5（a）可知，随着结构跨度增加，结构底层滞回能增加，结构中下部滞回能需求减小，结构中上部滞回能需求增加，结构顶部滞回能需求基本不变。结构中下部影响较明显，层间最大滞回耗能需求处，长跨较短跨滞回能需求减少了14.6%。由图5（b）可知，在大部分地震波作用下支撑滞回耗能依然保持在96%以上。

2.4 层高影响

采用算例15×3×3.0×7.2、15×3×3.3×7.2、15×3×3.6×7.2来研究层高对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。分别对三种结构在大震下（510 gal）进行弹塑性时程分析，计算结果取平均值，结果见图6。

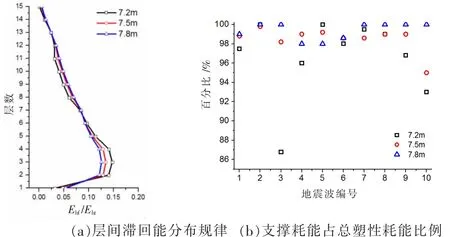
图5 跨度影响

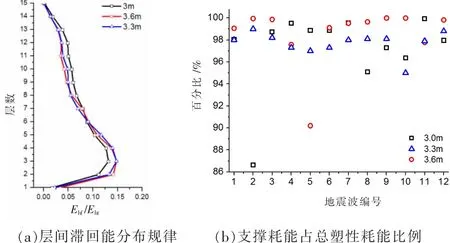
图6 层高影响

由图6(a)可知，随着结构层高增加，结构底层和中下部滞回能需求增加，最大增加幅度为0.035，为该层最大滞回比例的23%，结构中上部滞回能需求减小，顶部基本不变。结构层高越小，层间滞回能需求越趋向于均匀分布；结构层高越大，层间滞回能需求呈现出上小下大的分布规律就越明显。由图6(b)可知，在大部分地震波作用下支撑滞回耗能依然保持在95%以上。

2.5 跨数影响

采用算例15×3×3.6×7.2和15×5×3.6×7.2研究跨数对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。分别对两种结构在大震下（510 gal）进行弹塑性时程分析，计算结果取平均值，结果见图7。

图7（a）可知，随着结构跨数增加，虽然明显改变了结构所受到的地震作用和抗侧刚度，但是结构的滞回能层间分布曲线基本不变。由图7（b）可知，在大部分地震波作用下支撑滞回耗能依然保持在95%以上。

2.6 切线模量影响

切线模量的大小反应着钢材强化能力的大小，影响着结构进入塑性后的地震反应，本节针对算例10×3×3.6×7.2分别取E2=0、0.01E1、0.02E1、0.03E1四种本构模型进行弹塑性时程分析，研究切线模量大小对结构滞回能层间需求分布和支撑耗能占比的影响。所选地震波与结构反应谱分析时所得基底剪力吻合较好，结果如图8所示，可见切线模量取值大小对结构层间滞回耗能分布影响小，可以不予考虑。防屈曲支撑总耗能在四种情况下均在总滞回耗能的98%以上。

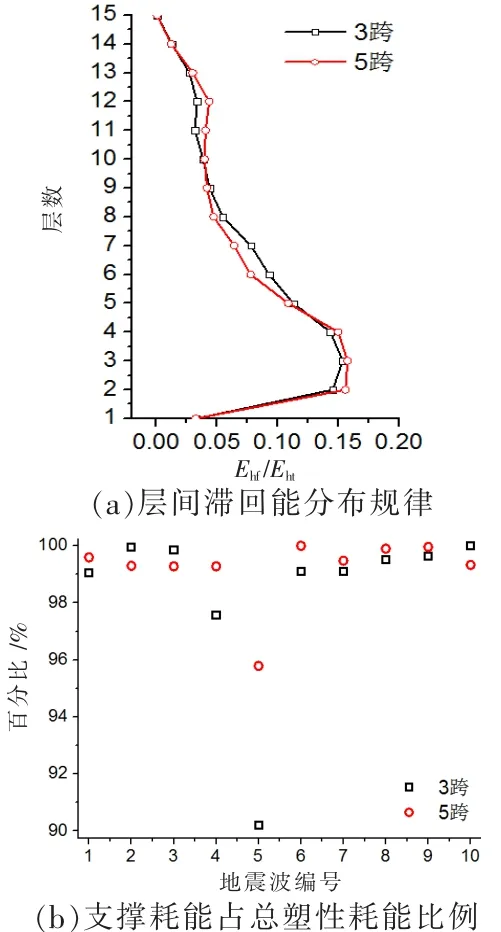
图7 跨数影响

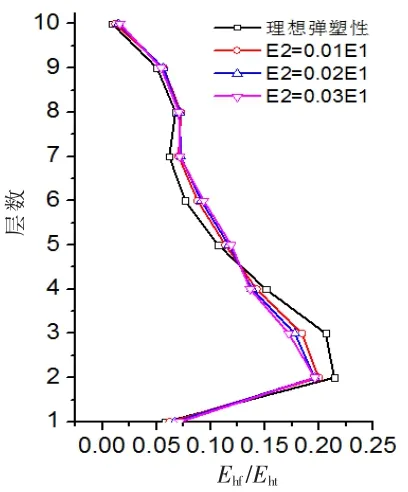
图8 切线模量影响

2.7 加速度影响

根据表6所选择的地震波，分别对算例10×3×3.6×7.2、15×3×3.6×7.2和20×3× 3.6×7.2进行弹塑性时程分析，研究地震波加速度峰值大小对结构滞回能层间需求分布规律和防屈曲支撑总耗能占结构总滞回耗能比例的影响。图9给出了三种结构所选自然波及人工波生成的beta谱与规范谱的拟合情况。结果见图10和图11，其中Ehf和Eht分别为每层的总滞回耗能和结构的总滞回耗能。TR表示天然地震波，AR表示人工地震波。最终结果取各条地震波分析结果的平均值。

表6 各算例所选地震波

由图9可以看出，结构滞回能呈现出上小下大的分布趋势。随着地震波加速度峰值的增加，防屈曲支撑钢框架结构底层滞回耗能需求逐渐增加，结构中下部滞回耗能需求逐渐减小，结构中上部滞回耗能需求逐渐增大，顶部滞回耗能需求基本不变，结构滞回能趋于均匀分布。这一现象一方面是由于防屈曲支撑具有不屈曲的特性，导致结构进入塑性以后层间刚度和防屈曲支撑耗能相对稳定；另一方面可能是由于随着地震波加速度峰值的增大，导致中上部防屈曲支撑更多地参与到滞回耗能中来。由图10可知，所有的结构在三种加速度的地震波作用下防屈曲支撑的耗能占结构总滞回耗能比例几乎都在90%以上。框架耗能主要是包括底层柱底和结构中下部支撑跨梁两端产生塑性铰耗能，在大震下这种现象尤为明显，所以处理好底层柱底与地基连接和梁柱的连接非常重要。防屈曲支撑承担了绝大部分滞回能量的消耗，有效地保护了主要承重构件在大震下的安全。

2.8 不同楼层数影响

对三种不同高度的结构作楼层归一化处理。定义，其中i为楼层，N为楼层的总数。分析结果见图12。从图中可以看出，随着楼层数的增加层间滞回能分布越加的均匀，虽然离散性还是存在，但是各条地震波作用下的滞回能层间分布曲线越来越集中。可以发现结构的最大层间滞回能总是出现在结构高度1/5到1/4之间，滞回能占比在10%到22%之间浮动，浮动宽度随着楼层数的增加逐渐减小。

图9 三种结构所选地震波平均beta谱与标准beta谱比较

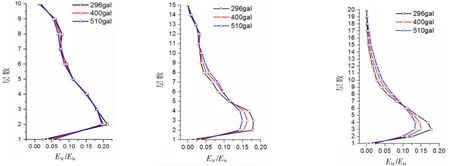
图10 不同层数结构在296、400、510 gal地震强度下的滞回能需求分布曲线

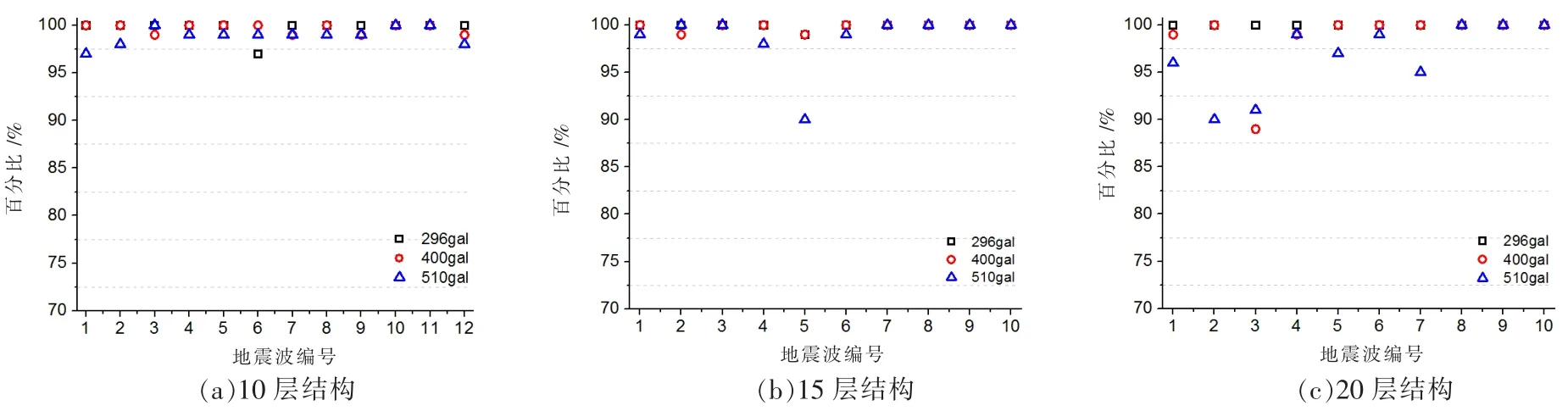
图11 不同层数结构在296、400、510 gal地震强度下支撑总耗能占结构总耗能的比例

图12 楼层数影响

3 结论

对远场强震下人字形防屈曲支撑钢框架滞回能层间分布规律的研究表明，大部分地震波作用下防屈曲支撑滞回耗能保持在结构总滞回耗能的95%以上；滞回能层间需求沿着高度方向从下至上先增加后逐渐减小；层间最大滞回能需求处出现在结构高度的1/5～1/4之间，根据平均分布曲线，该区段滞回能需求占比约为总滞回能的13%～19%。

加速度峰值和楼层数对人字形防屈曲支撑钢框架滞回能层间分布影响大；层高、跨度和持时影响小；跨数、阻尼和切线模量几乎无影响。随着加速度峰值、强震持时和跨度的增加结构中下部耗能比例减小，结构中上部耗能比例增加；随着层高增加，结构中下部耗能比例增大，中上部耗能比例减小；随着楼层数的增加，滞回耗能分布有均匀趋势，但依然保持上小下大的分布模式。

[1]张耀春,丁玉坤.防屈曲支撑、普通和特殊中心支撑钢框架结构抗震性能分析[J].建筑钢结构进展，2009，11（5）：8-15.

[2]国忠岩.防屈曲支撑钢框架结构抗震性能分析[D].哈尔滨：哈尔滨工业大学，2004

[3]贾明明，吕大刚，张辉，等.防屈曲支撑钢框架抗地震侧向倒塌能力分析[C]//第七届全国防震减灾工程学术研讨会暨纪念汶川地震五周年学术研讨会论文集，2013.

[4]Housner G W.Limit design of structures to resist earthquake[C]//Proceedings of the 1st World Conference on Earthquake Engineering.berkeley, CA,USA,1956.

[5]Kent Richard Estes.An energy method for seismic design[D].Univercity of Southern California,USA,2003.

[6]肖明葵,刘纲,白绍良.抗震结构的滞回耗能谱[J].世界地震工程，2002，18（3）：110-115.

[7]Park Y J,Ang A S,Wen Y.Seismic damage analysis of reinforced concrete buildings[J].Journal of Structural Engineering,ASCE,1985,111（4）：740-757.

[8]Kunnath S K,Chai Y H.Cumulative damage based inelastic cyclic demand spectrum[J].Earthquake Engineering&Structural Dynamics,2004,33（4）：49-520.

[9]翟长海，谢礼立，吴知丰，等.基于台湾集集地震的结构滞回耗能影响分析[J].哈尔滨工业大学学报，2006，38（1）：59-62.

[10]周海兵，顾强.强震下抗弯钢框架滞回能层间分布[J].苏州科技学院学报（工程技术版），2013，26（4）：28-34

[11]杭晓晨，顾强.强震下人字形中心支撑钢框架滞回能需求层间分布[J].苏州科技学院学报（工程技术版），2014，27（1）：31-38

[12]丁蕾，顾强.强震下K型偏心支撑钢框架滞回能需求层间分布[J].苏州科技学院学报（工程技术版），2014，27（2）：25-31.

[13]刘衍军，顾强.V形偏心支撑钢框架滞回能需求层间分布[J].建筑钢结构进展，2014，16（2）：23-31.

[14]杭晓晨，顾强.人字形中心支撑钢框架滞回能需求层间分布规律[D].苏州：苏州科技学院，2013.

The influence factors of hysteretic energy demand distribution via height of chevron steel structure with buckling restrained braces under far field and severe earthquakes

XU Hua,JING Ming
（School of Civil engineering,SUTS,Suzhou 215011,China）

In order to apply the energy-based method to the chevron buckling restrained braced steel frame structure,in the far field earthquake conditions,the energy analysis is carried out on eight kinds of chevron buckling restrained braced steel frame to obtain the influence of seimsic waves and structural characteristics on the hysteretic energy demand distribution of the steel structure with buckling restrained braces through the height and the proportion of hysteretic energy for the braces using ABAQUS dynamic implicit function and the different seismic waves.The results show that the hysteretic energy of the buckling restrained braces accounts more than 95%of the total structural hysteretic energy.Maximal acceleration of seismic waves and number of stories have great impact on the hysteretic energy demand distribution of the steel structure with the buckling restrained brace through the height,and in the duration of seismic records,the structural height and structural span have little impact;and the structural damping ratio,the number of structure acrosses and the tangent modulus of material have no impact on it.

Chevron steel structure with buckling restrained brace;energy balance;hysteretic energy distribution;nonlinear dynamic time history analysis

TU391

：A

：2096-3270（2017）02-0019-07

（责任编辑：秦中悦）

2016－11-01

苏州科技学院研究生科研创新计划项目（091320030）

徐 华（1992-），男，江苏无锡人，硕士研究生。

蒋 明（1961-），女，教授，博士，从事光测力学与结构工程的研究；E-mail：Jiangming@mail.usts.edu.cn。