抗弯钢框架近场地震反应分析

李 立，顾 强

（苏州科技大学 土木工程学院，江苏 苏州215011）

抗弯钢框架近场地震反应分析

李 立，顾 强

（苏州科技大学 土木工程学院，江苏 苏州215011）

选取20条带有明显速度脉冲的近场地震波作为地震动输入，建立近场地震动的反应谱，并与《建筑抗震设计规范》（GB50011-2010）设计反应谱进行了比较。按照现行抗震规范考虑近场地震作用增大系数1.5和1.25，分别设计了3层、6层抗弯钢框架，研究了结构在近场地震动下的反应。结果表明，近场地震动反应谱的加速度敏感区较宽，在中长周期段谱值大于规范设计反应谱的谱值；近场设计地震作用采用增大系数1.5时，对3层结构偏于保守，对6层结构偏于不安全，近场设计地震作用采用增大系数1.25时，对3层、6层结构都偏于不安全。

速度脉冲；近场地震动；增大系数；抗弯钢框架

工程界对近场地震动破坏性的认识始于1971年的美国圣费南多震害，Bertero对圣费南多地震中Olive-View医院的破坏进行研究，表明医院结构的破坏是由于长周期速度脉冲引起的[1]。受限于近场地震记录的匮乏，相应的研究工作并未展开。但1994年美国北岭、1995年日本阪神、1999年我国台湾集集、1999年土耳其伊兹米特和2008年我国汶川等地震提供的大量近场地震记录，从而推动了近场地震动特性和近场地震作用下结构反应及抗震设计方法的研究工作。Liao等研究了5层和12层钢筋混凝土框架在近场地震作用下的动力特性[2]；Amiri等研究了5层、8层和12层钢框架在近场地震作用下塑性铰的分布[3]；李爽等研究了5层和15层钢筋混凝土框架在近场地震作用下的反应，并与远场地震反应进行了比较[4]；王长龙研究了低、中、高三个Benchmark钢框架在近场地震作用下层间位移沿高度的变化[5]；吴徐等研究了3层、6层和10层抗弯钢框架结构在近场罕遇地震下层剪力的分布[6]。

少数国家或地区的抗震设计规范已考虑了近场地震动的影响，建立了近场地震设计反应谱。我国《建筑抗震设计规范》（GB50011-2010）[7]（以下简称《抗规》）的设计反应谱是根据大量远场地震动记录统计得出的，目前还没有给出考虑近场地震效应的反应谱。《抗规》只是在抗震性能化设计中简单要求：对处于发震断层两侧10 km以内的结构，地震动参数应计入近场影响；5 km以内宜乘以增大系数1.5，5 km以外宜乘以不小于1.25的增大系数。《抗规》也没给出增大系数的依据或解释。

选取20条近场速度脉冲型地震记录作为地震动输入，对近场速度脉冲型地震动的β谱进行分析，并与《抗规》β谱进行比较；然后，按《抗规》近场地震作用增大系数设计了3层和6层抗弯钢框架，分析了所设计结构在近场地震下的反应，评价规范增大系数方法的可行性，为《抗规》修订提供技术储备。

1 近场速度脉冲型地震动

1.1 近场脉冲地震波选择

按以下原则选取近场脉冲地震波：

（1）王京哲等的研究表明近场脉冲型地震动的PGV/PGA比值较大，通常达到0.2甚至更大[8]。为了更好地考虑近场地震动的速度脉冲效应，取PGV/PGA＞0.2。

（2）基于邵广彪和冯启明对断层距在0～5 km和5～10 km的近场地震波的地面峰值加速度和地面峰值速度统计的结果[9-10]，所选地震波的地面峰值加速度（PGA）＞0.2g，地面峰值速度（PGV）＞50 cm/s。

（3）Ⅱ类场地（设计结构为Ⅱ类场地）、震级（M）大于6。

依据上述选波原则，对发震断裂两侧5 km以内结构和5～10 km结构分别选取10条近场脉冲地震波。地震波的详细信息见表1。

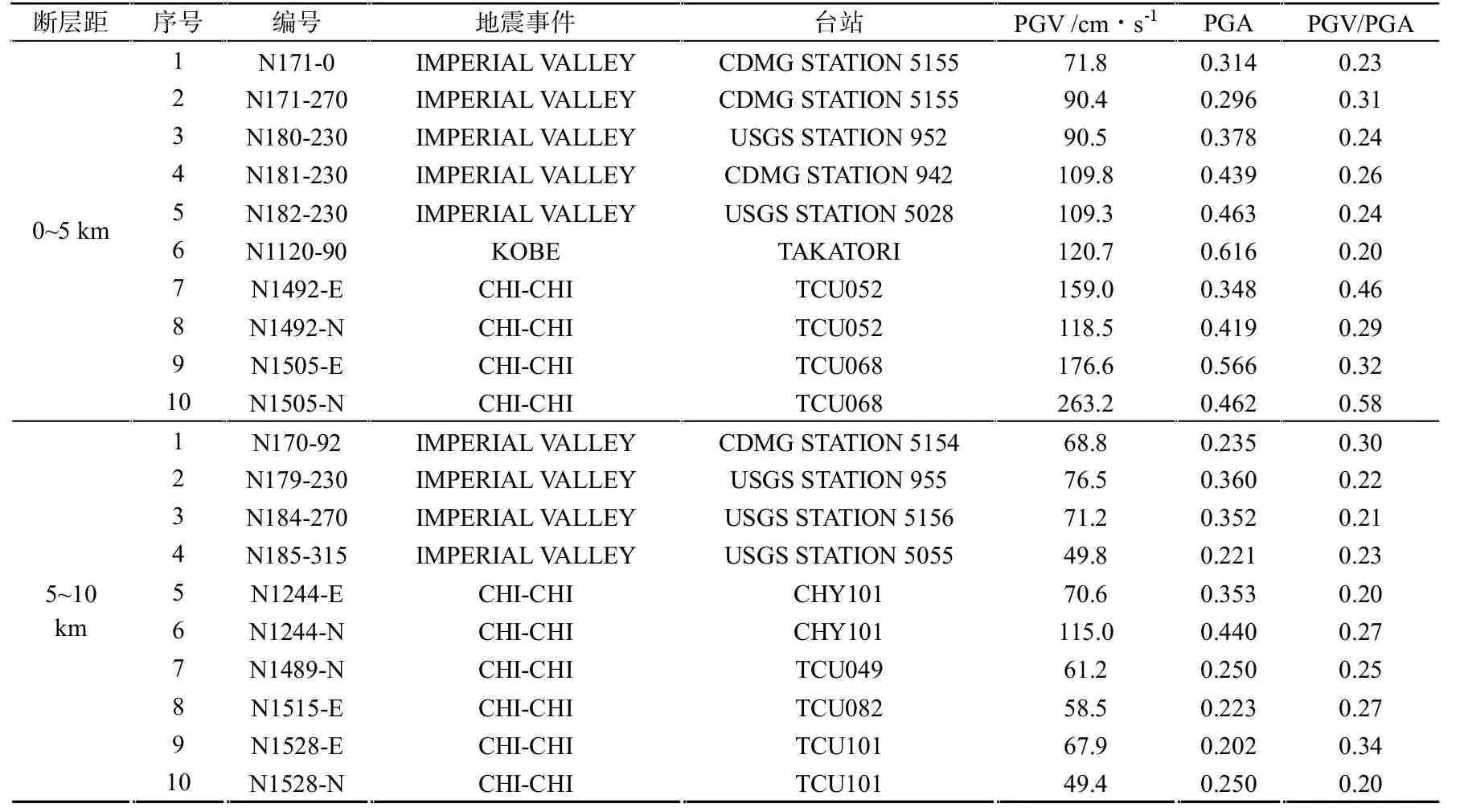
表1 近场脉冲地震波

1.2 反应谱分析

断层距0～5 km和5～10 km的10条近场地震波的β谱与《抗规》β谱比较见图1和图2。从图1和图2中可看出，与规范β谱相比，近场地震波β谱的平台段较宽。因为近场地震波含有长周期速度脉冲，在中长周期段近场地震波β谱的谱值远大于规范谱的谱值。由于近场地震反应谱形状与远场地震反应谱有明显的不同，建议对近场结构设计应采用近场地震设计反应谱。

图1 断层距0～5 km地震波谱

图2 断层距5～10 km地震波谱

2 结构设计

2.1 设计信息

按《抗规》近场地震作用放大系数设计3层、6层抗弯钢框架，结构抗震设防烈度为8度（0.3g），设计地震分组为第一组，场地类别为Ⅱ类；屋面恒载为4.5 kN/m2，活载为2.0 kN/m2；楼面恒载为4.0 kN/m2，活载为2.0 kN/m2；梁柱自重为1.1 kN/m，内外墙自重忽略不计；钢材为Q345钢。

框架跨度7.5 m，层高均为3.3 m，次梁间距2.5 m。研究对象为横向平面框架，故选取③轴线横向框架为设计对象。结构平面布置见图3，3层和6层结构的立面布置见图4。

框架梁柱均选用焊接工字型截面，梁柱节点为刚性连接。对发震断裂两侧5 km内结构的地震作用采用增大系数1.5，对5～10 km结构的地震作用采用增大系数1.25，采用SAP2000软件初选构件截面，然后进行应力比校核，最终选出满足要求的构件截面见表2。

图3 结构平面图

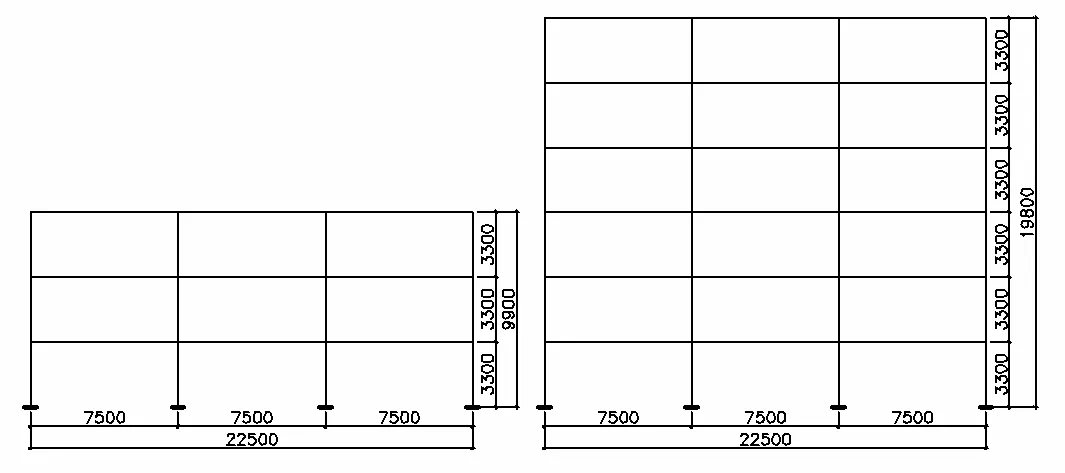
图4 结构立面图

表2 构件截面尺寸

2.2 Pushover分析

限于篇幅，图5仅给出了设计地震作用增大系数1.5的6层框架出铰顺序及位置。从图5中可以看出，部分梁端首先出现塑性铰，随着侧向位移的增加，柱脚也出现了塑性铰，最后大部分横梁端部出现塑性铰，柱脚全部屈服。结构出铰顺序合理，符合强柱弱梁的要求，也验证了文中结构设计的合理性。

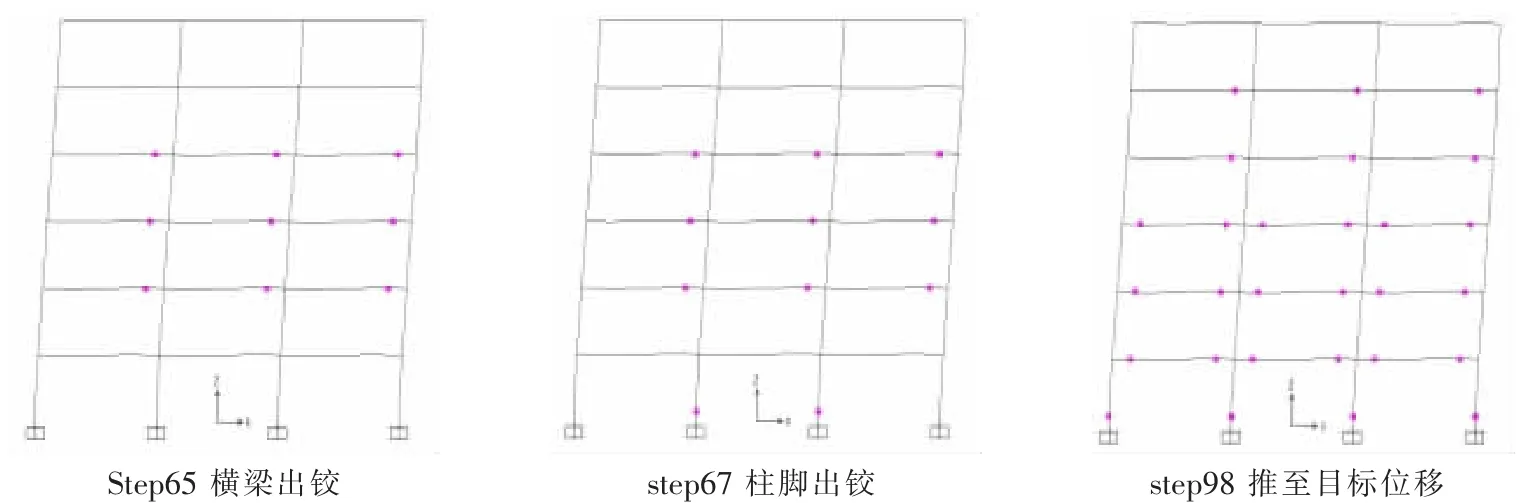
图5 塑性铰出铰顺序及位置

3 近场地震下结构的层间变形

3.1 弹性层间位移角

图6为设计地震作用增大系数1.5的3层、6层结构在近场多遇地震下层间位移角分布。从图6可知，3层、6层结构在多遇地震下的最大弹性层间位移角平均值分别为0.003 8、0.006 3，前者低于规范限值1/250，后者超过规范限值1/250。

图7为设计地震作用增大系数1.25的3层、6层结构在近场多遇地震下层间位移角分布。从图7可知，3层、6层结构在多遇地震下的最大弹性层间位移角平均值分别为0.004 6、0.006 6，均超过规范限值1/250。

3.2 弹塑性层间位移角

图8为设计地震作用增大系数1.5的3层、6层结构在近场罕遇地震下层间位移角分布。从图8可知，3层、6层结构在罕遇地震下的最大弹塑性层间位移角平均值分别为0.015、0.024，前者低于规范限值1/50，后者超过规范限值1/50。图9为设计地震作用增大系数1.25的3层、6层结构在近场罕遇地震下层间位移角分布。从图9可知，3层、6层结构在罕遇地震下的最大弹塑性层间位移角平均值分别为0.015、0.029，前者低于规范限值1/50，后者超过规范限值1/50。

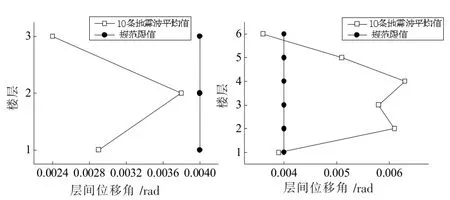
图6 地震作用增大系数1.5在近场多遇地震下层间位移角

图7 地震作用增大系数1.25在近场多遇地震下层间位移角

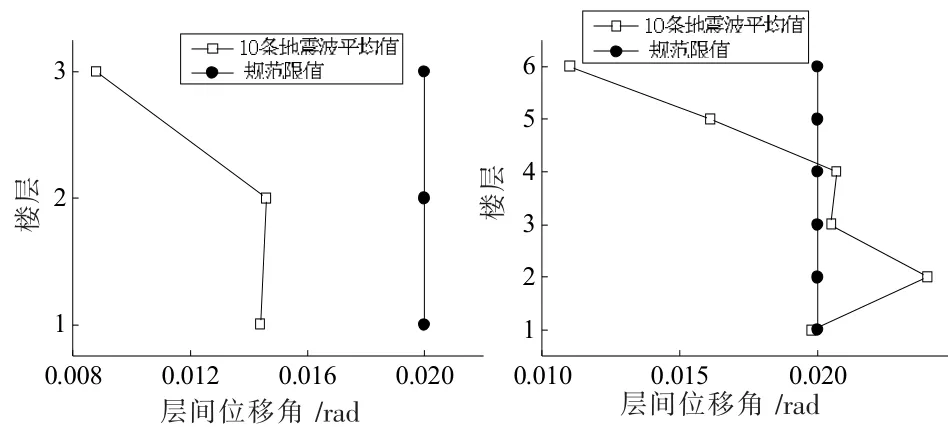
图8 地震作用增大系数1.5在近场罕遇地震下层间位移角

图9 地震作用增大系数1.25在近场罕遇地震下层间位移角

综上所述，当设计地震作用采用增大系数1.5时，3层结构的弹性、弹塑性层间位移角均满足规范限值要求；6层结构的弹性、弹塑性层间位移角均不满足规范限值要求。当设计地震作用采用增大系数1.25时，3层结构的弹性层间位移角不满足规范限值要求，弹塑性层间位移角满足规范限值要求；6层结构的弹性、弹塑性层间位移角均不满足规范限值要求。

3.3 构件截面变化对层间位移角的影响

对比设计地震作用采用增大系数1.5和1.25的3层结构的层间位移角沿楼层的分布，可知柱截面尺寸的改变对层间位移角走势的影响并不明显，其变化趋势基本一致。

对比设计地震作用采用增大系数1.5和1.25的6层结构的层间位移角沿楼层的分布可知，前者3至4层的层间位移角增加，后者3至4层的层间位移角减小。出现这种现象的原因是设计地震作用采用增大系数1.5的6层结构1至3层的梁截面为H550×270×14×18，4至6层的梁截面为H500×250×12×16，而设计地震作用采用增大系数1.25的6层结构1至6层的梁截面均为H500×250×12×16，相比而言设计地震作用采用增大系数1.5的结构的第4层梁截面突然减小使得第4层的层间位移角明显增大。

3.4 卓越周期的影响

图10为设计地震作用增大系数1.5的6层结构部分近场地震波的层间位移角沿高度的分布。从中可知，N1492-N地震波的层间位移角比其他地震波的层间位移角都大得多，出现这种现象的原因是N1492-N的卓越周期为1.14 s，结构的自振周期T1=1.16 s，两者相差不大，激发结构第一振型响应，共振导致层间位移角较大，罕遇地震下第一振型响应使结构底部的层间位移角明显增大；N1505-E和N181-230的卓越周期分别为0.42、0.24 s，而结构的自振周期T2=0.41 s、T3=0.23 s，故N1505-E、N181-230分别激发了结构第二、第三振型响应。N181-230激发的第三振型相对高阶，结构在其响应下层间位移角相对较小。表明地震波的卓越周期对层间位移角的影响较大。

图10 地震作用增大系数1.5的6层结构层间位移角沿高度的分布

4 结论

（1）与实际近场地震反应谱相比，规范设计反应谱在上升段（0～0.1 s）是安全的，平台段（0.1 s～Tg）偏低且略窄，下降段（Tg～6 s）衰减太快。（2）《抗规》考虑近场地震影响时，对发震断裂两侧5 km以内结构的设计地震作用采用增大系数1.5，5～10 km结构采用增大系数1.25的方法是不可行的。当设计地震作用采用增大系数1.5时，对3层结构偏于保守，对6层结构偏于不安全，当设计地震作用采用增大系数1.25时，对3层、6层结构都偏于不安全。（3）设计地震作用采用增大系数1.5的6层钢框架近场地震反应表明梁截面变化和地震波卓越周期对结构层间位移角的影响较大。（4）因近场地震反应谱形状与远场地震反应谱有明显不同，建议对近场结构设计应采用近场地震设计反应谱，或在现有反应谱的基础上针对结构周期不同采用不同的增大系数，以满足近场地震下结构设计的需求。

[1]Beertor V,Mahni S,Herrera R.Aseismic Design ImpIliactions of San Fernando Earqthquake Records[J].Earthquake Engng Struct Dyn,1978.6(1): 31-42.

[2]WEN LIAO,CHIN Hsiung,WAN Shiuan.Earthquake responses of RC moment frames subjected to near-fault ground motions[J].The Structural Design of Tall Buildings,2001,10:219-229.

[3]Amiri J A,M R Sahafi D A.Behaviour of MRF structures designed according to IRAN seismic code(2800)subjected to near-fault ground motions [C].The l4 WCEE,Beijing China,2008.

[4]李爽.近场脉冲型地震动对钢筋混凝土框架结构影响[D].哈尔滨：哈尔滨工业大学，2005.

[5]王长龙.近断层地震动作用下钢框架结构的地震响应分析[D].北京：北京交通大学，2008.

[6]吴徐，顾强.抗弯钢框架近场罕遇地震层剪力分布[J].苏州科技学院学报（工程技术版），2014，27（3）：5-12.

[7]中华建筑科学研究院.GB50011-2010建筑抗震设计规范[S].北京：中国建筑工业出版社，2010.

[8]王京哲，朱晞.近场地震速度脉冲下的反应谱加速度敏感区[J].中国铁道科学，2003，24（6）：27-30.

[9]邵广彪，冯启明.近断层地震动加速度峰值衰减规律的研究[J].地震工程与工程振动，2004，24（3）：30-37.

[10]冯启明，邵广彪.近断层地震动速度、位移峰值衰减规律的研究[J].地震工程与工程振动，2004，24（4）：13-19.

Analysis of near-field seismic response of moment resisting steel frames

LI Li，GU Qiang
（School of Civil Engineering,SUST,Suzhou 215011,China）

20 near-field earthquake records with velocity pulses are selected as ground motion inputs.The response spectrum of the near-field ground motion is established and then compared with the design spectrum of Code for Seismic Design of Buildings (GB50011-2010).According to the current seismic design code that the ground motion is multiplied by amplification factor 1.5 and 1.25,a 3-story and a 6-story moment-resisting steel frames are modeled and the seismic responses of the structure under the near-field earthquake are studied.It is indicated that the response spectrum of the near-field ground motion has a wilder acceleration-sensitive region, and the spectral value is greater than that of the design spectrum.When the ground motion is multiplied by amplification factor 1.5,it is conservative for the 3-story structure and is unsafe for the 6-story structure;and when the ground motion is multiplied by amplification factor 1.25,it is unsafe for the 3-story and 6-story structure.

velocity pulse；near-field ground motion；amplification factor；moment resisting steel frame

TU391

：A

：2096-3270（2017）02-0001-05

（责任编辑：秦中悦）

2016-11-28

国家自然科学基金项目（51278320）

李 立（1992-），男，江苏苏州人，硕士研究生。

顾 强（1953-），男，教授，博士，从事钢结构教学与科研工作，E-mail：guqiang383@163.com。