内填耗能芯框中心支撑与带耗能梁段交叉支撑钢框架抗震性能对比分析

吴沁林，于安林，刘双喜

（苏州科技大学 土木工程学院，江苏 苏州 215011）

内填耗能芯框中心支撑与带耗能梁段交叉支撑钢框架抗震性能对比分析

吴沁林，于安林，刘双喜

（苏州科技大学 土木工程学院，江苏 苏州 215011）

为研究内填耗能芯框中心支撑钢框架的抗震性能并与内填带耗能梁段交叉支撑钢框架和钢框架对比，利用有限元分析软件ABAQUS对3榀框架进行滞回模拟。首先建立引入钢材损伤的有限元实体模型对内填带耗能梁段交叉支撑双层单跨钢框架试验试件进行了模拟，有限元数值模拟结果与试验结果相吻合。在验证ABAQUS有限元数值模拟方法模拟结果可靠的基础上，分别建立了单层单跨的钢框架、带耗能梁段交叉支撑钢框架和内填耗能芯框中心支撑钢框架的有限元模型各1榀，得到了3榀钢框架在低周往复荷载作用下的滞回曲线，并对其水平承载力、抗侧刚度、延性及耗能能力进行了对比。结果表明：内填耗能芯框中心支撑钢框架具有较高的水平承载力、抗侧刚度、耗能能力和延性。

内填耗能芯框中心支撑钢框架；抗震性能；损伤；有限元分析

中心支撑（CB）是指支撑斜杆与横梁及柱汇交于一点的支撑体系，是多高层建筑常用的抗侧力构件。中心支撑具有较大的轴向刚度,构造简单，可在一定范围内减小结构的水平位移，并能改善结构的内力分布。在较大的水平地震作用下，中心支撑容易产生侧向屈曲,使结构抗侧刚度和耗能能力急剧下降,层间侧移显著增加,导致结构整体失稳破坏。因此，中心支撑一般用于抗风或抗震设防烈度较低的结构[1-2]。偏心支撑（EB）通过支撑斜杆一端仅连于梁上，形成耗能梁段。在强烈地震作用下，耗能段最先屈服，并通过耗能段的剪切变形耗能，可延缓或阻止斜向支撑的屈曲[3]。美国加州大学的Popov教授对这种结构作了系统的试验[4]，进行了1榀20层4跨单斜杆式偏心支撑钢框架试件的线弹性和动力试验分析和2榀单跨1/3缩尺单斜杆式偏心支撑钢框架试件的动力试验分析，通过试验验证了偏心支撑结构不仅具有中心支撑钢框架强度高、刚度大的优点，还兼具纯框架的延性和耗能能力，并开始应用于抗震设计中。1990年，于安林教授[5]通过对普通K型、EK型和Y型偏心支撑框架的大型试验试件进行伪动力试验研究，得出了虽然Y型支撑对框架横梁及楼板变形影响最小，但仍然会导致楼板出现较多裂缝，甚至震后钢梁出现一定程度的残余变形的结论，劣化了Y型偏心支撑钢框架水平承载力。2014年，冯业超等[6]对带耗能段交叉支撑钢框架的滞回性能进行了试验研究，并通过有限元模拟与传统Y型偏心支撑钢框架的滞回性能进行了比较[7]。该支撑体系通过将耗能梁段置于框架区格内，形成了内填带耗能梁段交叉支撑钢框架（CLBBF），这种结构的耗能段两端仅与支撑相连，可有效避免剪切变形对钢梁和楼板产生的影响，仍具有偏心支撑钢框架抗震性能优良的特点，见图1。

根据内填带耗能梁段交叉支撑钢框架（CCFBF）的设计理念，结合中心支撑和耗能梁段的受力特点，通过在X型中心支撑中间设置耗能芯框，形成一种新型的内填耗能芯框中心支撑钢框架结构（见图2）。

图1 带耗能梁段交叉支撑钢框架图

图2 内填耗能芯框中心支撑钢框架

该结构主要利用耗能芯框的剪切变形来耗散地震输入能，其受力机理与偏心支撑的耗能段类似，文中在使用ABAQUS有限元软件对文献[6]已有试验进行有限元模拟，验证有限元模拟结果与试验值相吻合的前提下，重点对各种耗能支撑钢框架抗震性能进行对比分析。

1 有限元模型的建立与模拟结果准确性验证

为验证ABAQUS有限元程序模拟结果的准确性，对文献[6]中已完成的内填带耗能梁段交叉支撑钢框架试验进行了数值模拟，并将有限元模拟结果与试验结果比较。试件为单跨双层1∶3缩尺钢框架，跨度为1 800 mm，层高为1 000mm，总高为2 100 mm，框架梁截面为150×100×6×9，框架柱截面为125×125×16×20，支撑截面为75×75×6×8，耗能梁段截面为75×75×6×8，耗能梁段长度为300 mm。试验试件的具体尺寸见图3。

1.1 有限元模型的建立

试件的有限元模型见图4，钢梁、钢柱、支撑和耗能芯框均采用C3D8R三维实体单元模拟，采用Seed part instance命令整体布置网格划分种子并进行结构化网格划分。模型各板件、部件之间均采用绑定（Tie命令）连接模拟焊接。钢柱底部边界条件采用完全约束（ENCASTRE命令）模拟试验试件柱底固接的边界条件。

1.2 钢材的本构

根据文献[6]，钢材均采用Q235B钢，采用双线性随动强化弹塑性模型，屈服强度fy为288 MPa，抗拉强度fu为429 MPa，弹性模量Es=2.41×105N/mm2，泊松比υ=0.3。钢材应力应变关系曲线见图5。

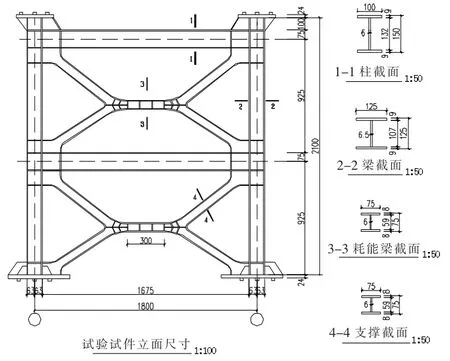
图3 试件尺寸图

图4 有限元模型

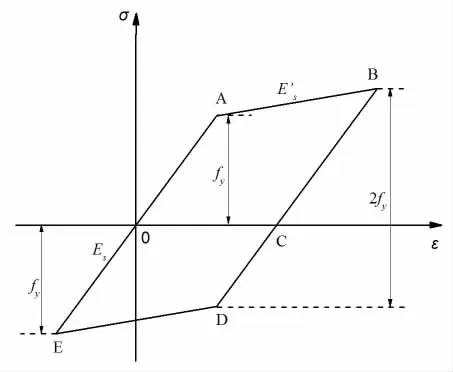
图5 钢材应力应变曲线

1.3 钢材的延性损伤

在钢材材性中加入有限元软件ABAQUS自带的Ductile Damage（延性损伤）属性来模拟钢材损伤对其力学性能的影响，以求试件加载后期的数值模拟结果出现与试验现象相似的水平承载力下降现象。钢材的延性损伤属性主要由损伤起始准则和损伤演化准则组成。引入延性损伤后的钢材应力应变曲线如图6所示。

（1）应力三轴度损伤起始准则。文献[8]根据Yu H L等的建议对Xue-Wierzbicki损伤准则[9-10]进行了简化，提出应力三轴度损伤起始准则，减少了需通过钢材剪切试验确定的参数，可利用该准则确定钢材的等效塑性损伤应变，其简化形式为

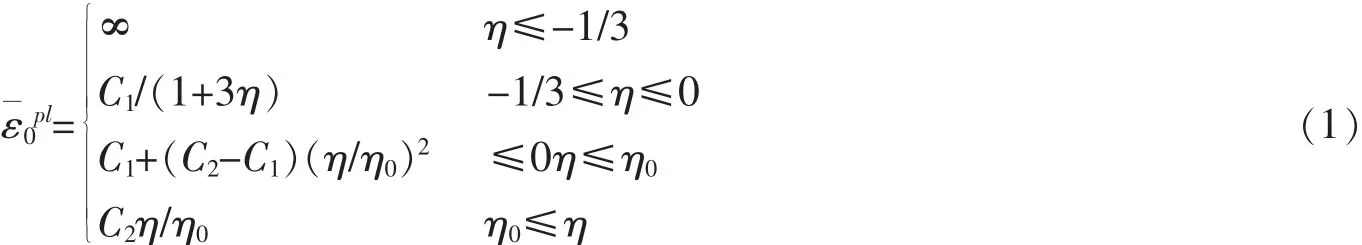
式中，C1为钢板纯剪切状态下的等效塑性损伤应变；C2为钢材开口圆棒单向拉伸时的等效塑性损伤应变；η为应力三轴度；η0为单向拉伸时的应力三轴度。

通常情况下，C1、C2可通过以下公式进行转化

式中，n为钢材的硬化参数。

由式（1）、（2）算出的钢材应力三轴度与等效塑性损伤应变的关系曲线见图7。

（2）损伤演化准则。此外，文献[8]还进行了10组钢板的拉伸试验，最终回归出钢材损伤因子D与塑性位移比之间的函数关系，获得了钢材的损伤演化准则如下式

由式（3）得出的钢材损伤演化路径，见图6中损伤起始点（D=0）至钢材损伤点（D=1）间曲线。本文采用上述公式计算出定义延性损伤所需参数，具体参数数值见表1。

图6 钢材应力应变曲线

图7 钢材应力三轴度与等效塑性损伤应变路径

表1 钢材延性损伤参数表

1.4 有限元模拟的准确性验证

通过对内填带耗能梁段交叉支撑钢框架试验试件[6]的有限元模拟，得到了其滞回曲线和骨架曲线，并同文献[6]中试验结果进行了对比，见图8～10。

图8 滞回曲线

图9 骨架曲线

图10 抗侧刚度

由图8～9可知，有限元模拟的滞回曲线较试验曲线更为饱满，在加载初期滞回曲线的斜率更大，抗侧刚度高于试验试件，相同位移对应的水平荷载更大。而在加载后期，有限元模拟的水平荷载与试验值的差距不断减小，水平极限承载力略高于试验值，具体数值及比值见表2。同时也可以看出，由于引入了钢材的损伤模型，在加载后期，有限元分析获得的水平承载力出现了下降，且下降点对应位移与文献[6]中所描述的试验现象相吻合，验证了引入钢材损伤属性后的有限元模型能模拟试件在加载后期的水平承载力退化。

表2 水平承载力峰值的模拟值与试验值对比

由图10可知，有限元模型的初始抗侧刚度大于试验结果，其退化速度也明显略快于试验结果。随着加载位移的增大，两者趋于接近。当加载位移达到25 mm以后，两者几乎相同，刚度退化曲线接近重合。具体数值和比值见表3。

表3 抗侧刚度模拟值与试验值对比

有限元模拟结果与试验结果的主要差异在于加载初期的抗侧刚度，其产生原因有以下几个方面：（1）试验试件中存在较大残余应力，残余应力的存在可使试件较早地进入弹塑性状态，减小试件抗侧刚度；（2）文中有限元模型虽然引入了钢材损伤缺陷，但并未考虑焊缝缺陷、构件几何缺陷等，相较于试验试件仍然为理想化模型。

综上所述，文中采用的有限元模拟方法对钢结构滞回性能的模拟结果与试验结果十分接近。因此，使用该方法模拟不同支撑体系钢框架的滞回性能，模拟结果具有较高的可信度。

2 不同支撑体系钢框架设计与有限元建模

为研究内填耗能芯框中心支撑钢框架的抗震性能，分别建立单层单跨钢框架、内填带耗能梁段交叉支撑钢框架和内填耗能芯框中心支撑钢框架有限元模型各1榀，对这3榀框架的滞回性能进行对比分析。其中3榀框架跨度层高及梁柱截面均相同，按照民用建筑全比例设计，跨度为6 000 mm，层高为4 200 mm，框架梁截面为400×300×16×20，框架柱截面为450×450×16×20。由于框架尺寸与文献[6]中有限元模型相同，内填带耗能梁段交叉支撑钢框架的耗能梁段截面与长度、支撑截面均按文献[6]中的设计选取，其支撑与耗能梁段截面为300×300×12×16，耗能梁段长度为1 200 mm。

2.1 内填耗能芯框中心支撑钢框架的设计

对耗能芯框中心支撑各构件截面尺寸进行设计，以确保结构在水平地震力作用下耗能芯框最先进入塑性，发生剪切型屈服；但支撑却不屈曲，从而使结构水平承载力不会降低，起到第一道防线的作用。最终选取支撑、芯框截面为300×300×12×16，芯框跨度为1 800 mm，高度为1 200 mm。耗能芯框中心支撑钢框架的具体尺寸见图11。

图11 耗能芯框中心支撑钢框架尺寸图

2.2 有限元模型的建立

分别建立单层单跨钢框架、内填带耗能梁段交叉支撑钢框架和内填耗能芯框中心支撑钢框架有限元模型，见图12～14。

图12 钢框架有限元模型

图13 带耗能梁段交叉支撑钢框架

图14 内填耗能芯框中心支撑钢框架

3 结果分析

3.1 滞回曲线

图15给出了3榀框架的水平荷载-位移滞回曲线。由图15可知，在结构屈服之前，3榀框架的水平荷载与位移之间基本呈直线，耗能芯框中心支撑和带耗能梁段交叉支撑的滞回曲线基本重合，钢框架的滞回曲线较前两者明显斜率偏低。随着加载位移的增大，三榀框架均逐步进入弹塑性阶段，滞回曲线开始逐渐偏离直线，后一次加载的曲线斜率较前一次逐步减小，形状呈“梭形”，滞回环面积明显增大。在3榀框架中，耗能芯框中心支撑钢框架的水平承载力最高，残余变形最小，但最先开始出现水平承载力下降，滞回环不如其他两榀框架饱满。带耗能梁段交叉支撑水平承载力次之，残余变形最大，水平承载力退化出现较晚，且其滞回曲线相较于芯框中心支撑更为饱满，耗能能力较强。钢框架的水平承载力明显低于前两者，残余变形较大，整个加载过程均未出现明显的水平承载力下降，滞回环包络面积小于前两者。

3.2 骨架曲线

图16为3榀框架的水平承载力-位移骨架曲线。表4给出了3榀框架的分析结果。由图16可知，耗能芯框中心支撑的屈服荷载、峰值荷载均为最高，后者为耗能梁段交叉支撑的1.2倍左右，为钢框架的2倍左右。这说明在循环荷载作用下，耗能芯框中心支撑能承担大部分的水平荷载。耗能芯框中心支撑的屈服荷载、峰值荷载都高于内填耗能梁段交叉支撑，但其屈服荷载位移、峰值荷载位移都比后者要小，这说明其对抗侧刚度的提升要高于后者。由于内填芯框增大了结构的变形能力，芯框中心支撑钢框架的延性系数和内填耗能梁段交叉支撑相当，说明该支撑类型有效克服了中心支撑延性较差的缺点。

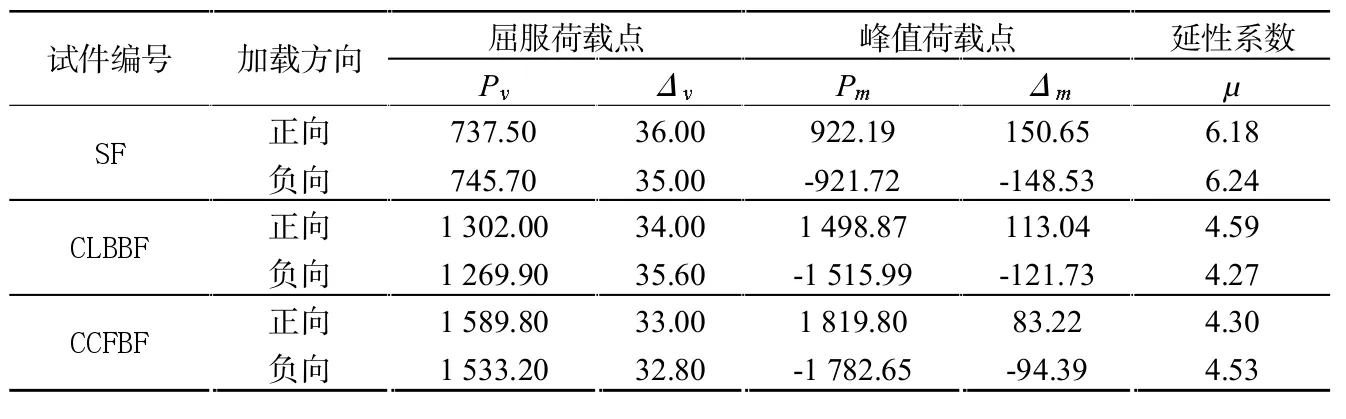
表4 主要分析结果

图15 滞回曲线

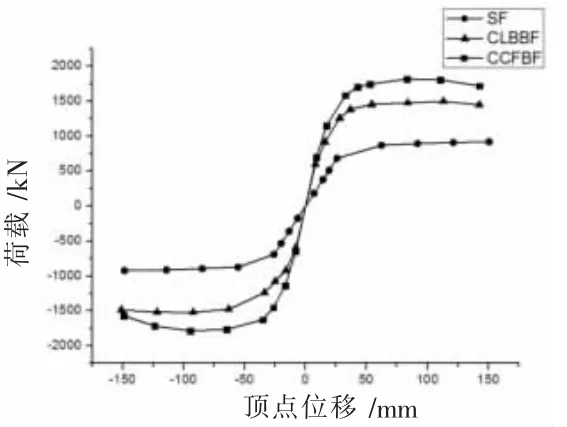
图16 骨架曲线

3.3 刚度退化

用文献[11]的公式计算了3榀框架的割线刚度K，刚度退化曲线见图17。可以看出，芯框中心支撑的初始抗侧刚度比内填耗能梁段交叉支撑略大，刚度退化规律基本一致，在加载初期都出现较明显的刚度退化现象。芯框中心支撑的抗侧刚度始终比內填耗能梁段交叉支撑的抗侧刚度高。钢框架初始抗侧刚度较低，但在加载初期未出现明显的刚度退化现象。随着加载位移的增加，钢框架开始出现刚度退化现象，但退化速度小于前两者。

3.4 耗能能力

图18为3榀框架在各级加载位移下的累积耗能。由图18可知，前两级加载中，3榀框架耗散的能量均很小。从第三级加载开始，耗能芯框中心支撑钢框架和内填耗能梁段交叉支撑钢框架开始产生塑性耗能，结构显著进入弹塑性阶段。当达到第五级加载时，钢框架的累积耗能明显增加，而耗能芯框中心支撑钢框架的累积耗能增加明显，累积耗能与内填耗能梁段交叉支撑几乎相同。在后三个加载级中，3榀框架累积耗能均显著增加。但总体上，内填耗能芯框中心支撑钢框架耗能最多，钢框架耗能最小。

图19为3榀框架在各级加载位移下的等效粘滞阻尼系数。由图19可知，在第一级加载中，三榀框架的等效粘滞阻尼系数均接近于0，三榀框架都处于弹性状态。从第二级加载开始，耗能芯框中心支撑钢框架和内填耗能梁段交叉支撑钢框架的等效粘滞阻尼系数开始显著上升，内填耗能梁段交叉支撑钢框架的等效粘滞阻尼系数略高于耗能芯框中心支撑钢框架。第四级加载开始，耗能芯框中心支撑钢框架和内填耗能梁段交叉支撑钢框架的等效粘滞阻尼系数增长速度减慢，且两者数值在第五级加载中逐渐相同，而钢框架等效粘滞阻尼系数开始显著增长。第五级以后的各加载级，三榀框架的等效粘滞阻尼系数增速接近，耗能芯框中心支撑钢框架的等效粘滞阻尼系数最大，内填耗能梁段交叉支撑钢框架次之，钢框架最小。

图17 刚度退化对比图

图18 累积耗能对比图

图19 等效粘滞阻尼系数

4 结语

（1）采用引入钢材损伤准则的有限元模拟方法可对试件的滞回性能进行较为准确的模拟。其模拟结果的最大水平承载力、加载后期的水平承载力退化、刚度及刚度退化与试验值接近，初始抗侧刚度大于试验。（2）有限元模拟结果的初始抗侧刚度大于试验值，其主要原因是有限元模型相比试验试件过于理想化，未考虑残余应力、焊缝缺陷、构件几何缺陷等不利因素的影响。（3）内填耗能芯框中心支撑钢框架的滞回曲线较饱满，水平承载力比带耗能梁段交叉支撑钢框架提高了大约20%，比钢框架提高了大约100%，具有较高的水平承载力。其正、负向延性系数均大于4，具有良好的变形能力。（4）内填耗能芯框中心支撑钢框架的初始抗侧刚度较大，带耗能梁段交叉支撑钢框架略低于前者，但两者在加载初期刚度退化均较明显。（5）内填耗能芯框中心支撑钢框架在加载前期耗散的能量和等效粘滞阻尼系数低于带耗能梁段交叉支撑钢框架，但在加载后期耗能和等效粘滞阻尼系数均显著增加，其耗能能力优于带耗能梁段交叉支撑钢框架。

[1]沈国庆，陈宏，王元清.支撑形式对钢框架结构抗震性能影响[J].低温建筑技术，2005，108（4）：37-40.

[2]沈江元，于安林.内填钢板剪力墙中心支撑钢框架的抗震性能研究[J.钢结构，2009（8）：7-15.

[3]易方民.高层建筑偏心支撑框架结构抗震性能和设计参数研究[D].北京:中国建筑科学研究院，2000.

[4]Charles W,Roeder,Egor P Popov.Eccentrically braced steel frames for earthquakes[J].Journal Of Structural Division,1978,104（3）：319-353.

[5]于安林.EK形、Y形支撑的抗震性能试验研究[J].工程抗震，1990，22（3）：253-260

[6]冯业超.内填带耗能梁段交叉钢支撑钢框架的抗震性能研究[D].苏州：苏州科技学院,2013.

[7]冯业超，于安林.交叉形与Y形耗能支撑钢框架滞回性能分析[J].苏州科技学院学报（工程技术版）,2014，27（4）：20-24.

[8]周天华，李文超，管宇.基于应力三轴度的钢框架循环加载损伤分析[J].工程力学，2014，31（7）：146-155.

[9]Wierzbicki T,Xue L.On the effect of the third invariantof the stress deviator on ductile fracture[R].Cambridge,MA,USA,2005.

[10]Xue L.Damage accumulation and fracture initiation inuncracked ductile solids under triaxial loading—PartI:Pressure sensitivity and Lode dependence[R].Cambridge,MA,USA,2005.

[11]赵宝成，于安林，王军良，等.内填Y形钢支撑加固多层钢筋混凝土框架结构滞回性能试验研究[J].建筑结构学报，2013（8）：107-118.

Comparative analysis on seismic property of concentrically braced steel frames filled with core steel frames or embedded cross shape braces with link beams

WU Qinling,YU Anlin,LIU Shuangxi
（School of Civil Engineering,SUST,Suzhou 215011,China）

In order to investigate the seismic performance of concentrically braced steel frames filled with core steel frames(CCFBF)and compare with the steel frames embedded cross shape braces with link beams,the hysteretic simulation of the two frames was carried out using the finite element analysis software ABAQUS.Firstly,a finite element model with damage criterions of concentrically braced steel frames filled with core steel frames (CLBBF)were established with the finite element software ABAQUS.The results from the finite element numerical simulation are in agreement with the experimental results.The simulated results show the reliability and superiority of this method.Then the finite element models of a concentrically braced steel frames filled with core steel frames,a steel frame embedded cross shape braces with link beams and a steel frame were established to carry out the nonlinear numerical analyses for they hysteretic behavior.The horizontal bearing load capacity, stiffness degeneration,ductility and energy dissipation capacity of three frames were compared.The results indicate that the concentrically braced steel frames filled with core steel frame has excellent horizontal bearing load capacity,lateral stiffness,ductility and energy dissipation capacity.

concentrically braced steel frames filled with core steel frame (CCFBF);seismic performance;damage criterions;finite element analysis

TU392

：A

：2096-3270（2017）02-0013-06

（责任编辑：秦中悦）

2017－01-03

吴沁林（1991-），男，江苏如皋人，硕士研究生。

于安林（1957-），男，教授，硕士，从事钢结构设计与应用的研究，E-mail：Yual@mail.usts.edu.cn。