碎石土库岸边坡稳定性及影响因素分析

王代兵

(深圳市深水兆业工程顾问有限公司，广东 深圳 518000)

1 概 述

随着经济的发展，我国用电量需求显著增大。而水电站建造位置较为偏僻，多数位于山区。水电能源的获取是通过水电站的蓄水与排水实现的，在蓄水与排水过程中，水位的变化位置与变化速度会影响水电站坡体的稳定性，从而引发自然灾害。因此，针对水电站的坡体稳定性展开研究，对我国水电能源的获取及自然灾害的防治具有重要意义。

邹德玉[1]分析了降雨对边坡稳定性的影响，并利用软件进行建模，分析土体水利特性对边坡稳定性的影响。裴智超[2]利用软件模拟水库水位变化过程，分析了水位升降对边坡稳定性的影响。夏怡等[3]采用饱和-非饱和渗流分析法，对降雨条件下的边坡进行有限元模拟，分析了降雨对边坡稳定性的影响。刘彦等[4]采用3种不同极限平衡方法，对比分析了不同工况下弃土场边坡稳定性。简文彬等[5]以岸坡为研究对象，分析了水位对边坡稳定性影响。高诗钦等[6]以岩质边坡为研究对象，基于JRC-JMC模型，分析了各参数对边坡稳定性的影响。叶帅华等[7]根据基本假设和几何关系，提出了分析边坡稳定性的方法。吕建航等[8]以加筋膨胀土边坡为研究对象，开展模型试验，分析了内土压力、含水率等因素对边坡稳定性的影响。

上述研究主要采用饱和渗流理论，但未考察基质吸力对边坡稳定性的影响。本文以国内某地区水电站库区边坡为主要研究对象，以饱和-非饱和渗流分析法为理论基础，通过剖析水位的变化速率、渗透性以及黏聚力等各种因素对边坡稳定性的影响，为我国自然灾害的有效预防工作奠定理论基础。

2 计算理论

由于库区边坡同时受非饱和及饱和区地下水相互作用，需同时考虑二者之间的统一性。渗流理论控制方程如下：

(1)

式中：kx为水平渗透系数；h为水头高度；ky为竖向渗透系数；mw为比水容量；ρw为水密度；g为重力加速度。

边坡稳定性采用极限平衡法进行计算，主要考虑条间剪力和法向应力对边坡的影响。利用Morgenstern-Price法，根据力的平衡条件，边坡稳定性安全系数Ff计算公式如下：

(2)

根据力矩平衡，稳定性安全系数计算公式如下：

(3)

式中：c为黏聚力；φ为摩擦角；α为土体底部倾斜角；μ为孔隙水压力；N为条块底部法向力；D为线荷载；β、ω、R、x、f、d为几何参数。

3 计算模型

以国内某地区水电站库区边坡为研究对象，取其边坡断面特征进行有限元分析，并对其土质-水分特性曲线进行拟合，见图1。随着基质吸力的增加，碎石土和强风化砂泥石的体积含水量逐步下降，而强风化砂泥石的体积含水量则整体高于碎石土的体积含水量。

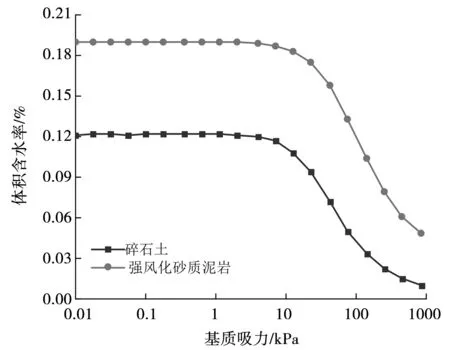
图1 土-水特征曲线

采用Van-Genuchten模型，得到渗透系数曲线，见图2。

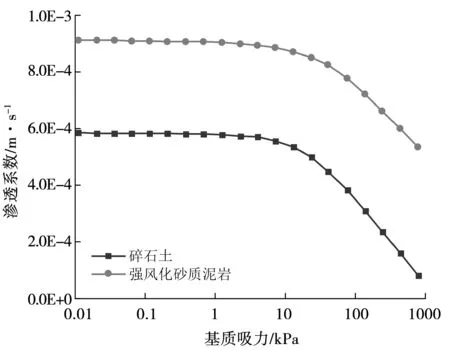
图2 渗透系数曲线

由图2可知，随着基质吸力的增大，体积含水率逐渐减少，强风化砂质泥岩的体积含水率整体大于碎石土的体积含水率。

采用Mohr-Coulomb本构模型作为有限元计算模型。边坡横向长度为340 m，边坡高度最低处为48 m，最高处为184 m。碎石土与强风化砂质泥岩参数见表1。

本研究考虑库水位升降速度、渗透系数、黏聚力对安全系数的影响，计算方案见表2。

表1 材料物理力学参数

表2 计算方案

3.1 水位升降对坡体稳定性的影响

根据前人研究成果，确定不同水位升降速度，分别为0.5、1、2、2.5、3、5 m/d，研究其对安全系数的影响。水位升降速度与安全系数关系曲线见图3、图4。

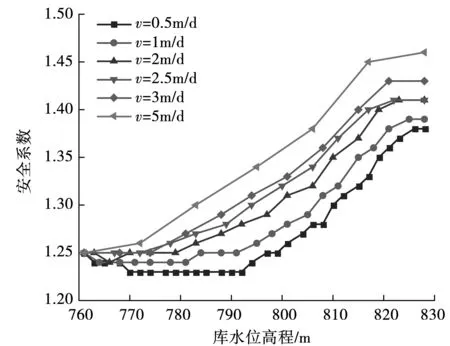
图3 蓄水速度与安全系数关系图

由图3可知，随着蓄水速度的增大，其安全系数逐渐增大。当水库蓄水时，水库安全系数与其水位高程呈正相关关系，随着高程的增大，安全系数逐渐增大。当蓄水速度为0.5 m/d时，安全系数有最小值，为1.225；当蓄水速度为5 m/d时，安全系数有最大值，为1.456。当库水位高程一致时，蓄水高度由0.5 m/d增长至5 m/d时，其最小安全系数增幅为2%。在水的渗流作用下，坡体自重应力增大，且受到孔隙水压力及孔隙水浮力的作用，使其摩擦力减小，土体易发生滑动，导致安全系数降低。在蓄水速度较小的情况下，水位上升速度较小，水在土体内的渗流作用较为充分，导致坡体易发生损害。所以，当蓄水速度较大时，其安全系数大于蓄水速度较小时的安全系数。

图4 放水速度与安全系数关系图

由图4可知，随着放水速度的增大，其安全系数逐渐减小。当放水速度一定时，随着水位高程的增大，其安全系数呈先减小后增大的趋势。当放水速度为0.5 m/d时，坡体安全系数最大；当放水速度为5 m/d时，坡体安全系数最小，降幅约为6%。当水位下降时，土体内孔隙水减少，所受的摩擦力增大，所受的孔隙水压力与浮力减小，使其安全系数降低。当放水速度越大时，土体中的孔隙水来不及排出，自重应力增大，摩擦力减小，土体易发生滑动，导致安全系数降低。因此，当放水速度较大时，其安全系数小于放水速度较小时的安全系数。

由上述分析可知，为保证坡体安全性，当水库蓄水时，蓄水速度宜较大；当水库放水时，放水速度宜较小。

3.2 碎石土渗透性对岸坡稳定性的影响

不同渗透系数对坡体安全系数影响见图5。

图5 渗透系数对安全系数影响图

由图5可知，随着时间的增大，坡体的安全系数呈现先减小后增大的趋势。当排水速度较小时，曲线整体较为平缓；当排水速度较大时，曲线的安全系数差异较大。当放水速度一致时，渗透系数越小，其安全系数越小。当渗透系数越大时，坡体的渗透性越好，使得排水过程中坡体内的水可以被及时排出。由于坡体内孔隙水减少，孔隙水压力减小，坡体所受力减少，使得安全系数提高，坡体稳定性得以保证。当渗透系数较小时，坡体内的水不能被及时排出，在排水过程中受孔隙水压力与浮力的影响，使其摩擦力减小，容易发生滑动，坡体稳定性较差，其安全系数较小。

在3种不同排水速度下，同一时间最大安全系数与最小安全系数分别相差3.5%、8.4%和10.5%。安全系数的差值随排水速度的增大而增大，当排水速度越大时，最大安全系数与最小安全系数的差值越大。

由上述分析可知，若想提高库区坡体的稳定性，需采用渗透性较好的材料，或控制其排水速度，使其排水速度较小，使其安全系数增大，从而保证坡体的稳定性。

3.3 抗剪强度对岸坡稳定性的影响

为研究不同抗剪强度对坡体稳定性的影响，抗剪强度取值分别为10.4、12.8、15.8、19.6和24.2 kPa。取c=15.8 kPa，φ=30.2°。根据式(4)、式(5)，计算黏聚力和内摩擦角。

(4)

式中：c为黏聚力；c′为折减黏聚力；Ks为折减系数。

(5)

式中：φ为内摩擦角；φ′为折减内摩擦角。

黏聚力与安全系数曲线见图6。

图6 黏聚力与安全系数关系图

由图6可知，当排水速度一致时，安全系数随着时间的变化趋势呈先减小后增大的趋势。对比不同黏聚力对安全系数的影响，当排水速度不变时，在相同的时间下，安全系数随着黏聚力的增大而增大。取时间为30 d、排水速度为1 m/d，当黏聚力为10.4 kPa时，其安全系数为1.151；当黏聚力为24.2 kPa时，其安全系数为1.251，两种不同黏聚力的安全系数相差9%左右。黏聚力与安全系数呈正相关关系，黏聚力越大，其安全系数越高。当黏聚力较大时，坡体内各物质之间的相互吸引力较大，颗粒间互相胶结，使土体间相互作用力较大，摩擦力增大，所以坡体安全系数较大，稳定性较好。

取黏聚力为24.2 kPa，当排水速度为5 m/d时，坡体最小安全系数为1.213；当排水速度为1 m/d时，坡体最小安全系数为1.265。不同排水速度下，安全系数差值约为4.3%。

由上述分析可知，当黏聚力较大时，坡体安全系数较大，稳定性较强。因此，可以通过提高黏聚力，来增强坡体的稳定性。

内摩擦角与安全系数曲线见图7。

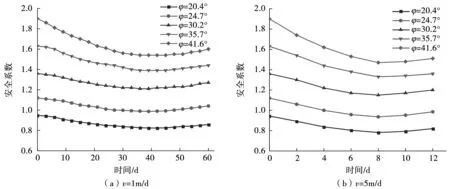
图7 内摩擦角与安全系数关系图

由图7可知，内摩擦角与安全系数关系趋势较为平缓，总体呈先下降后上升的趋势。当排水速度为1 m/d时，内摩擦角与安全系数呈正相关关系。随着内摩擦角的增大，坡体的安全系数逐渐增大。当时间为30 d时，最小安全系数为0.813，最大安全系数为1.523，二者之间相差85.6%。表明内摩擦角对坡体安全系数有显著影响，内摩擦角与坡体稳定性呈正相关关系。

当内摩擦角相同时，取内摩擦角为41.6°，取时间为10 d，当排水速度为1 m/d时，坡体安全系数为1.8；当排水速度为5 m/d时，坡体安全系数为1.55。坡体安全系数与排水速度呈负相关关系，随着排水速度的增大，坡体的安全系数逐渐减小。

由上述分析可知，若想提高库区坡体的稳定性，需提高土体的黏聚力，提高其内摩擦角，降低排水速度，使其安全系数增大，从而保证坡体的稳定性。

4 结 论

1) 随着放水速度的增大，其安全系数逐渐减小。随着蓄水速度的增大，其安全系数逐渐增大。为确保坡体安全性，当水库蓄水时，蓄水速度宜较大；当水库放水时，放水速度宜较小。

2) 在3种不同排水速度下，同一时间最大安全系数与最小安全系数分别相差3.5%、8.4%和10.5%。安全系数的差值随着排水速度的增大而增大，当排水速度越大时，最大安全系数与最小安全系数的差值越大。若想提高库区坡体的稳定性，需采用渗透性较好的材料，或控制其排水速度，使其排水速度较小，使其安全系数增大，从而保证坡体的稳定性。

3) 内摩擦角对坡体安全系数有显著影响，内摩擦角与坡体稳定性呈正相关关系；内摩擦角对坡体安全系数有显著影响，内摩擦角与坡体稳定

性呈正相关关系。若想提高库区坡体的稳定性，需提高土体的黏聚力，提高其内摩擦角，降低排水速度，使其安全系数增大，从而保证坡体的稳定性。