基于对角自同构群的离散对数问题的盲签名方案

潘 平， 洪 歧

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

基于对角自同构群的离散对数问题的盲签名方案

潘 平， 洪 歧

(陕西理工大学 数学与计算机科学学院， 陕西 汉中 723000)

为了能够抵抗已知的量子算法攻击，非交换密码已成为后量子密码时代的研究方向之一。采用非交换群构造了一个签名方案，并在此基础上设计了一个盲签名方案。新方案的安全性依赖于单位三角矩阵群的对角自同构群上的离散对数问题。新的盲签名方案满足盲性和多一不可伪造性安全，并且只需要更短的公钥和更少的存储空间；采用平方-乘算法计算两个自同构的乘积，减少了计算成本。

非交换群； 对角自同构群； 离散对数； 盲签名

非交换密码(non-commutative cryptography)作为密码学研究领域的专业术语，首次出现于2010年“符号计算与密码”国际会议。2011年，Myasnikov、Shpilrain和Ushakov合著《非交换密码及群论问题复杂性》[1]，从此，非交换密码开始登上了现代密码学的舞台。密码学原语的数学平台从“交换”到“非交换”的拓广并不是一个简单的概念类推，而是有着深刻的背景和丰富的内涵，可以说是后量子密码学的一个极其重要的研究方向之一。

盲签名是一类特殊的数字签名，除了满足数字签名的一般要求之外，还有自身的特点，即签名者不知道自己所签消息的具体内容。正是这一特点使得盲签名广泛应用于许多领域，比如电子支付、电子选举等。直观上讲，所谓盲签名，就是把需要隐藏的文件放进一个信封里，此时这个信封里的文件内容是任何人都不知道的。然后在信封里放一张复写纸，当签名者在信封上签名时，他的签名便透过复写纸签到了这个文件上。

一个好的盲签名应该具有以下性质：

(1)盲性：签名者对所签消息的具体内容是不知道的。盲性也蕴含如下属性，对于脱盲后的签名，即便是签名者本人也不能联系是哪个用户在何时请求该签名的。

(2)多一(One-More)不可伪造性：由于盲签名的脱盲操作从本质上赋予了普通用户“伪造”合法签名的能力，因此盲签名的不可伪造性的定义要略费周折。2000年，Pointcheval和Stern[2]给出了所谓的“多一”不可伪造性的概念：对某个整数l(这里假定l为安全参数k的多项式)，一个攻击者与签名者进行l次交互后获得l+1个有效的签名是不可行的。

自1982年Chaum[3]首次给出基于RSA的盲签名方案以来，人们基于交换群的密码难题假设提出了许多盲签名方案。然而，1994年，Shor[4]提出了高效求解大整数分解问题和交换群上的离散对数问题的量子算法，这些成果对现行的盲签名体制的安全性投下了阴影。近年来，运用非交换群(如辫群、特殊线性群、有限p群等)来构造公钥密码系统已引起人们的广泛关注，也相继出现了一些优秀的研究成果[5-15]。但是目前运用非交换群构造签名及盲签名方案的研究成果甚少。Paeng等人[8]用特殊线性群的内自同构群构造一个公钥加密系统，称为MOR密码系统。MOR密码系统是ElGamal加密系统在非交换群上的推广。此后，研究者[15-16]相继分析了基于矩阵群与循环群的半直积的内自同构群上的离散对数问题是亚指数时间复杂度。很自然地，希望非交换群的自同构群在公钥密码系统中能有更广泛的应用。文献[13]构造了基于非交换群的内自同构群的离散对数问题的盲签名方案，但已分析出其效率低。因此，通过选择适当的非交换群及其自同构，可以构造一个更安全高效的签名及盲签名方案。

本文首先在单位三角矩阵群的对角自同构群上的离散对数问题困难假设下提出了一个签名方案，最后对这些方案的安全性和效率进行了分析。本文工作是基于单位三角矩阵群的对角自同构群构造了一个签名方案，该方案类似于有限域交换群上的DSA算法，是DSA算法在非交换群上的推广。然后在这个签名方案的基础上，进行了盲化改造，给出了盲签名方案。新的签名和盲签名方案的安全性建立于单位三角矩阵群的对角自同构群的离散对数问题。

1 单位三角矩阵群及对角自同构

用于构造新方案的非交换群是特征为p(p为素数)的有限域Fq上的单位三角矩阵群。

定义1[10]设Fq为有限域，Fq上的一个n×n的单位三角矩阵是主对角线左下方的元素全为零、主对角线的元素全为1的矩阵，形如

单位三角矩阵群是指Fq上的所有n×n的单位三角矩阵构成的集合，记作UT(n,q)。

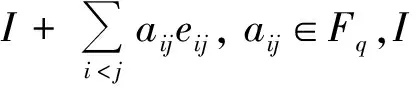
对任意I+aeij，I+bekj∈UT(n,p)，a,b∈Fq，有

这里[x,y]=x-1y-1xy是元素x,y∈G的交换子，G是群。

UT(n,q)是一般线性群的p子群，其阶为qn(n-1)/2。UT(n,q)也是一个多重循环群。如果存在一个有限长的子群列G=G0>G1>G2>…>Gk>Gk+1=1，其中Gi+1是Gi的正规子群且Gi+1/Gi(i=1,2,…,k)是循环群，这样的群称为多重循环群。

定义2[10]设D是一个n阶对角矩阵，其定义为：主对角线元素均是有限域Fq上的非零元素，其余元素均为0的矩阵，形如

对角矩阵D可表示为[ω1,ω2,…,ωn]，非零元素ωi∈Fq。

定义3[17]群G的自同构是指群G到自身的同构，用Aut(G)表示群G的全体自同构组成的集合。对于映射的乘法，Aut(G)组成一个群，叫做G的自同构群。

定义4[10]UT(n,q)上的对角自同构定义为

定义5[10]对角自同构群的离散对数问题：设G是一个单位三角矩阵群，Φ是G的对角自同构，给定Φ和Φx，计算x∈Fq。

2 盲签名方案

作为一个过渡，先构造基于对角自同构群的离散对数问题的签名方案，这个方案可以说是签名方案从交换群到非交换群的延伸。

系统参数:设G是群，Φ：G→G是自同构。设ħ：G→Fq和h：{0,1}*→Fq均是抗碰撞哈希函数。

密钥生成：随机选择x∈Fq，计算y=Φx。则私钥为x，公钥为y。

签名：待签名消息m，签名者做如下的计算：

1)选择k∈Fq，计算v=Φk；

2)计算s=k-1(h(m)+rx)，其中r=ħ(v)；

则消息m的签名(r,s)。

验证：验证者接收到消息m的签名(r,s)后：

1)计算u1=h(m)s-1和u2=rs-1；

2)由y和u2计算yu2；

3)计算w=Φu1(yu2)；

验证等式w=v是否成立。若成立，则接受(m,r,s)是一个有效的签名；否则拒绝接受签名。

在上述签名方案的基础上，非交换群上的盲签名方案描述如下：

系统参数：设G是群，Φ：G→G是自同构。设ħ：G→Fq和h：{0,1}*→Fq均是抗碰撞哈希函数。

密钥生成：选择随机数x∈Fq，计算Φx，则私钥为x，公钥为Φx。

盲化：

1)签名者选择随机数k∈Fq，计算Φk及e=ħ(Φk)，发送(Φk,e)给用户；

2)用户选择随机数a,b∈Fq，①计算Φa，②由Φk计算Φbk，③由Φa和Φbk计算Φa+bk，④计算f=h(m,r)，其中r=ħ(Φa+bk)；

3)用户计算m′=fber-1，并发送m′给签名者。

签名：签名者接收到盲化消息m′后，计算s′=m′k-ex，并发送s′给用户。

去盲：用户接收到s′后，计算s=s′re-1+af，则消息m的签名为(r,s)。

验证：验证者接收到消息m的签名(r,s)后，

1)计算Φs；

2)由Φx计算Φxr；

3)由Φs和Φxr计算Φs+xr；

4)计算Φ(s+xr)f-1，其中f=h(m,r)。

验证等式Φ(s+xr)f-1=Φa+bk是否成立。若成立，则接受(m,r,s)是一个有效的签名；否则拒绝接受签名。

定理1 任何人都可通过公开的签名(m,r,s)验证新的盲签名方案中签名的有效性。

证明 需要证明签名(m,r,s)满足验证等式Φ(s+xr)f-1=Φa+bk成立。

首先签名参数s：

s=s′re-1+af，

其中

s′=m′k-ex，

m′=fber-1，

则

s=(fber-1k-ex)re-1+af，

整理得到

则上述方程两边都变成Φ的幂方：

即(m,r,s)是一个有效的签名。

3 安全性及效率分析

定理2 上述盲签名方案满足盲性。

证明： 要证明方案的盲性，即给定签名(r,s)，存在唯一的盲因子a和b。

假定消息m的签名为(r,s)，在方案中签名者完全知道参数k、Φk、e、m′、s′=m′k-ex，则对盲因子a和b，下列等式必成立：

(1)

(2)

(3)

已知盲化消息m′、e、f与p互素，由等式(1)和(2)可得唯一的a和b：

从而验证了等式(1)—(3)均成立：

上述盲签名方案在一般群模型下满足多一不可伪造性安全。该方案的证明思路类似于文献[18]的安全性证明。

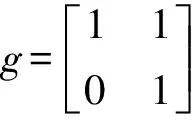
那么

所以新方案的安全性依赖于单位三角矩阵群的对角自同构群上的离散对数问题。假如公开Φ和Φx，攻击者要求x，需先计算Dx，这是一个共轭搜索问题，在一般线性群上是不难的，但是D与Dx不唯一，DZ与DxZ也是共轭问题的解，这里Z是UT(2,q)的中心。只要保证UT(2,q)的中心足够大，攻击者需要穷举才能找到中心Z。

表1 盲方案所需存储空间的大小比较

现在考虑新盲签名方案的参数大小。新方案中素数q为160比特。由于g∈UT(2,q)，Φ(g)∈UT(2,q)，那么只需要1个元素就可表示出Φ(g)，因此g和Φ(g)都只需要160比特。表1给出了新方案所需参数大小，同时，也列出了文献[13]中盲签名方案所需参数大小。通过比较，显然新盲签名方案在系统参数和公钥上仅需要更短的参数大小，私钥和签名两者保持相同的大小。

总而言之，本文盲签名方案总共需要960比特的存储空间，而文献[13]的方案需要2080比特，大约是新方案的2倍多。因此新盲签名方案更节省存储空间。根据文献[12]，采用平方-乘算法计算两个自同构的乘积，最坏情形下的复杂度为16p域乘。显然，新方案所需计算成本优于文献[13]的方案。

4 结 论

在单位三角矩阵群的对角自同构群上的离散对数问题困难假设下，首先给出了一个非交换群的盲签名方案，新方案建立于非交换群的签名方案的基础之上。新的盲签名方案满足盲性和多一不可伪造性，通过比较，新方案既能节省了大量的存储空间，也减少了计算成本。如果考虑其他的非交换群(如循环矩阵群、幂零群等)或者自同构的复合运算(如对角自同构与置换自同构的复合、图自同构与域自同构的复合等)，也许方案更安全，这将是以后需要进一步深入研究的工作。

[1] MYASNIKOV A G,SHPILRAIN V,USHAKOV A.Non-commutative Cryptography and Complexity of Group-theoretic Problems[M].Amer.Math.Soc.Surveys and Monographs,2011.

[2] POINTCHEVAL D,STERN J.Security Argument for Digital Signatures and Blind Signatures[J].Journal of Cryptology,Springer-Verlag,2000,13(3):361-396.

[3] CHAUM D.Blind Signatures for Untraceable Payments[C].Crypto 1982,California,1983.

[4] SHOR P.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer[J].SIAM Journal on Computing,1997,26:1484-1509.

[5] KO K H,CHOI D H,CHO M S,et al.New signature scheme using conjugacy problem [EB/OL].Cryptography ePrint Archive.[2016-08-20].http://eprint. iacr.org/2002/168,2002.

[6] BAUMSLAG G,FAZIO N,NICOLOSI A R,et al.Generalized learning problems and applications to non-commutative cryptography[C].In ProvSec’11, Springer, LNCS 6980, 2011:324-339.

[7] HASHIMOTO Y,SAKURAI K.On the construction of signature schemes based on birational permutations over noncommutative rings[EB/OL].[2016-08-20].http://eprint.iacr.org/2008/340,2008.

[8] PAENG S H,HA K C,KIM J H,et al.New public key cryptosystem using finite non-abelian groups[C].CRYPTO2001,Berlin:Springer-Verlag,LNCS 2139,2001:470-485.

[9] MAHALANOBIS A.A simple generalization of the ElGamal cryptosystem to non-abelian groups II[J]. Communications in Algebra,2012,40:3583-3596.

[10] MAHALANOBIS A.The automorphism group of the group of unitriangular matrices over a field[J].International Journal of Algebra,2013,7(15):723-733.

[11] MAHALANOBIS A.The MOR cryptosystem and extra-special p-groups[EB/OL].Proceedings of WCC 2012,Castro Urdiales,Spain 9-13 July 2012.[2016-08-20].http://arxiv.org/abs.

[12] MAHALANOBIS A.The MOR cryptosystem and finite p-groups[EB/OL].[2016-08-20].http://arxiv.org/abs.

[13] 潘平,王励成,杨义先.内自同构群上的盲签名[J].北京邮电大学学报,2012,35(6):20-23.

[14] PAN Ping,WANG Li-cheng,YANG Yi-xian,et al.Chameleon Hash Functions and One-Time Signature Schemes from Inner Automorphism Groups[J].Fundamenta Informaticae,2013,126(1):103-119.

[15] PAENG S H.On the security of cryptosystem using the automorphism groups[J].Information Proceedings Letters,2003,88(6):293-298.

[16] TOBIAS C.Security analysis of the MOR cryptosystem[C].PKC 2003,Berlin:Springer-Verlag,LNCS 2567,2003:175-186.

[17] 徐明曜,曲海鹏.有限p群[M].北京:北京大学出版社,2010.

[18] BROWN R L.Generic group,Collision resistance,and ECDSA[J].Designs,Codes and Cryptography,2005,35(1):119-152.

[责任编辑：魏 强]

Blind signature based on the discrete logarithm over diagonal automorphism group

PAN Ping, HONG Qi

(School of Mathematics and Computer Science, Shaanxi Sci-Tech University, Hanzhong 723000, China)

In order to resist currently known quantum algorithm attacks, non-commutative cryptography has become one of research directions in post-quantum cryptography era. A signature scheme over non-commutative group is proposed. Based on the signature scheme, a blind signature scheme is presented. The security of the schemes relies on the discrete logarithm problem over the diagonal automorphism group of the group of unitriangular matrices. The new blind signature scheme satisfies blinding and one-more unforgery, and only requires shorter public keys and smaller storage space. Since the multiplication of two automorphisms is computed using the square and multiply algorithm, the computing cost is reduced.

non-commutative group; diagonal automorphism group; discrete logarithm; blind signature

1673-2944(2017)01-0071-05

2016-09-20

2016-11-22

国家自然科学基金资助项目(61370194)；陕西省教育厅自然科学研究基金资助项目(2013JK0598,16JK1163)；陕西理工学院博士科研基金资助项目(SLGQD13-24)

潘平(1975—)，女，甘肃省天水市人，陕西理工大学讲师，博士，主要研究方向为信息安全、密码学；洪歧(1961—)，男，浙江省东阳市人，陕西理工大学副教授，博士，主要研究方向为大数据处理、体视化技术。

TP309

A