一种安全的匿名代理数字签名方案
廖小平,邓小亚,成淑萍
(四川文理学院 计算机学院,四川 达州 635000)
简单地说,数字签名方案提够了手写签名的密码学类比,其实他提够了更强的安全保障。数字签名作为一种强大的工具已被多个国家接受为具有法律效力;可用于合同或证明文件的证明,用于对个人或公司的认证,并可作为复杂安全协议的组成部分。数字签名同时能够用于安全的分发和传输公钥。
在实际的应用中,除了普通的数字签名外,还有些特殊的数字签名方案,代理数字签名方案就是其中的一种,代理数字签名这个概念是由Mambo、Usada和Okamoto[1]于1996年首次提出的。它的主要思想是当原始签名人因某种原因不能行使签名权利时,将签名权委派给其他人替自己行使签名权。由原始签名者(部分)授权代理签名者,使代理签名者产生代替原始签名者的签名就是代理签名。
近年来,人们提出了许多新型的代理签名方案[2],如强代理签名和弱代理签名等方案。新型的代理签名方案出现了新的一些特点[3-5],新型的代理签名方案不同于以往各类型的代理签名方案,它的特点是:1)在代理签名中隐藏代理签名者身份,验证者无法从代理签名中识别代理者身份,在出现争议时,验证者可以通过原始签名者揭示代理签名者的身份;2)为了防止代理签名被伪造,所以新方案要求任何人包括原始签名者都不可能伪造代理签名。这种特点的签名方案在实际应用中得到了广泛的应用。例如原始签名者希望对外保密代理签名者身份,又不能完全信赖代理签名者,代理签名者要防止原始签名者伪造代理签名对自己进行诬陷。本文提出的新方案满足这类需求。
1 预备知识
1.1 离散对数知识
定义[6]:设G是一个有限阶的循环群,且g是G中的阶为q的生成元,使得y=gx成立的一个最小非负整数x(0≤x≤q)成为元素y∈G的离散对数,记为x=logyg。
1.2 离散对数问题(DLP)
定义[7]:给定一个大素数p,p-1含另一个大素数因子q,则域Zp的乘法群Z*p是一个p-1阶循环群,设g是Z*p的一个生成元,1 定义:对于一个有限循环群Z*p,g是Z*p的生成元,给定元素ga和gb,计算出gabmod p,其中p为素数。 定义:给定一个有限循环群G,G的生成元为g,以及群元素 ga,gb,gc,判断 gc=gabmod p 是否成立。 任意选择两个大素数p和q且满足条件q|p-1,g∈Z*p并且满足 gq=1mod p(g≠1);定义 h(·)为安全的哈希函数;定义mw是授权书,主要用来描述原始签名者A对代理签名者B代理权限的约定,主要包括A的标识,B的代理期限、签名消息范围等内容;A为原始签名者,B为代理签名者;V为验证者;原始签名者A的私钥为xA,公钥为mod p并将yA公开;代理签名者B的私钥为xB,公钥为mod p并将yB公开;xp为原始签名者A和代理签名者B共同生成的代理私为对应的代理公钥;代理签名者B的标识为IDB;签名者的标识为 IDP;需要签名的消息为 m,σ=Sig(m,x)是签名者用私钥x对消息m的一个离散对数型数字签名;Ver(y,σ,m)与签名算法相对应的验证算法;y为签名者的公钥;返回值为真或者为假。 1)原始签名者A随机选择数kA∈,计算rA=gkAmod p,A把(mw,rA)通过安全信道发送给B。B如果认为授权是合法的,则生成自己的代理私钥sB,r1和s1。过程如下: 然后 B 把生成的密钥值及身份标识(rB,IDB,r1,s1)通过安全信道发送给A。A验证等式是否成立,若成立,则 A 秘密保存(rB,yB,IDB),以备用来揭示代理者的身份,最后A计算YP=yBrBrBmod p,并将其写入mw中。2)原始签名者A利用 1)中得到的kA和rA,计算 然后 A 把(rA,sA,mw)通过安全信道发送给 B,B 验证等式是否成立,若成立,B秘密保存(rA,sA,mw,sB)。 代理签名人B首先验证消息m是否符合授权证书mw的约定,若m满足要求,则B利用代理私钥xP产生代理签名σP=Sig(m,xP),得到代理签名值(m,σP,mw,rA,yA)。 1)验证者 V 得到代理签名值(m,σP,mw,rA,yA),首先验证消息m是否符合mw的约定,若m满足要求则进入下一步,否则认为代理签名σP无效。 2)验证者 V 利用代理签名(m,σP,mw,rA,yA)计算: 其中 yP是从 mw中取得, 然后检验等式 Ver (yP,σP,m)=true是否成立,若成立,则认为代理签名有效,否则无效。 1)验证者V向原始签名者A提供代理签名(m,σP,mw,rA,yA),A使用代理签名验证算法验证代理签名的有效性,如果有效,则进入下一步。 2)原始签名者A从mw中取出YP,然后依次取出在代理密钥对生成阶段保存的(rB,yB,IDB),判断等式 YP=yBrBrBmod p是否成立,如果存在(rB,yB,IDP)满足这个等式,则 IDP是实现代理签名(m,σP,mw,rA,yA)的代理签名者。 定理1代理签名者B使用代理私钥xP,代表原始签名者A 对消息 m 签名,验证者 V 利用代理签名(m,σP,mw,rA,yA)计算代理公钥: 然后使用yP验证相应的代理签名,那么yP=gxPmod p 证明 由于 即:yP=gxPmod p成立 证毕 由于代理签名(m,σP,mw,rA,yA)包含 yA,表明这是原始签名者A承认的代理签名。 3.2.1 代理签名的不可伪造性 1)根据yP,伪造者无法伪造xP。 这是因为mod p,而(rA,sA)是 A 对 mw的签名,yP包含在 mw中,rA,sA,mw,YP都是不可更改和伪造的,所以伪造者不可能通过计算yP伪造xP,又已知yP求xP是离散对数问题。 2)根据,xP=sA+sBmod q,如果伪造者想伪造代理签名者B的代理签名,伪造者必须同时具备以下两个条件: 第一个条件:伪造sA,因为 而A的私钥xA和kA对伪造者都是无法得到的,所以伪造者不可能伪造sA。又由于原始签名者A和代理签名者B之间的交互都是经过安全通道完成的,所以伪造者不可能冒充B或直接窃取sA。 第二个条件:伪造sB,由于 而B的私钥xB,kB和rB对伪造者都是无法得到的,所以伪造者也不可能伪造sB。 所以,根据xP=sA+sBmod q,伪造者不可能得到xP。 3)原始签名者A也不可能伪造代理签名者B的代理签名,虽然 A 可得到 sA,却无法得到 sB,这是因为 sB=(xB+kBrB)yAmod q,B的私钥 xB和kB(虽 A可知rB,但已知 rB推出 kB是离散对数问题)对于A是无法获得的,所以A也是不可能得到xP。 3.2.2 公钥的不可伪造性 总之,除了代理签名者B,任何人都无法伪造代理签名。 防止代理权限滥用包含两层含义: 1)防止代理权的转移:原始签名者A对代理签名者B的代理授权信息是 (mw,rA,sA),(rA,sA)是 A 对 m 的签名,所以(rA,sA,mw)都是不可更改的,且 YP包含在 mw中,代理公钥: 即一旦原始签名者A指定代理签名者B,yP就已经确定,除非 B 把 xP给他的代理者,否则 B 不能利用(rA,sA,mw)再次代理授权。 2)防止代理签名者越权:代理签名验证算法的第1步就是验证消息m是否符合代理授权书mw的约定,如果不符合,那么签名无效,所以A可以充分利用代理授权书mw有效约束B代理权限范围。 验证者 V 利用代理签名(m,σP,mw,rA,yA)计算代理公钥: 验证这个代理签名,(m,σP,mw,rA,yA)没有包含代理签名者身份,虽然已知,但rB对于V是无法得到的,已知YP是无法推出yB的,由此可见,验证者V能够验证代理签名的有效性,但并不知代理签名者的身份。 在必要时,在原始签名者A的帮助下,验证者V利用揭示代理者身份的算法,能够揭示代理签名者的身份。 首先,从代理签名生成方式可以看到,有效代理密钥生成包括了代理签名人B的身份信息,因此,他不能否认自己对消息m的代理签名。其次,从不可伪造性证明也可以看到,原始签名人及任何第三方不能伪造代理签名,所以代理签名人不能否认由原始签名人揭示的代理签名是由自己产生的。因此,该方案能满足不可否认性。 现在满足匿名性的代理数字签名方案很多,但大部分方案还存在一定的安全缺陷,主要原因在于要满足匿名性同时还必须公开足够的数据以提供验证者验证,本文提出的安全匿名代理数字签名方案在满足匿名性的同时还满足了其他很多的要求,比如不可伪造,不可否认等,所以该方案具有更高的安全性。 [1]Mambo M,Usuda K,Okamoto E.Proxy Signatures for Delegating Signing Operation[C]//Proceedings of the 3rd ACM Conference on Computer and Communications Security,New Dehi,India,1996:48-57. [2]张建中,薛荣红,彭丽慧.一种基于身份的代理环签名方案[J].计算机工程,2011,37(17):126-148.ZHANG Jian-zhong,XUE Rong-hong,PENG Li-hui.Id-based proxy ring signature scheme[J].Computer Engineering,2011,37(17):126-148. [3]谷利泽,张胜,杨义先.一种新型的代理签名方案[J].电子与信息学报,2005,27(9):58-62.GU Li-ze,ZHANG Sheng,YANG Yi-xian.A new proxy signature scheme[J].Journal of Electronics&Information Technology,2005,27(9):58-62. [4]鲁荣波,何大可,王常吉,等.对一种新型代理签名方案的分析与改进[J].电子与信息学报,2007,29(10):116-119.LU Rong-bo,HE Da-ke,WNANG Chang-ji,et al.Cryptanalysis and improvement of a new proxy signature scheme[J].Journal of Electronics&Information Technology,2007,29(10):116-119. [5]鲍皖苏,隗云,钟普查.原始签名人匿名的代理环签名研究[J].电子与信息学报,2009,31(10):2392-2396.BAO Wan-su,WEI Yun,ZHONG Pu-cha.Research on proxy ring signature with anonymity of the original signer[J].Journal of Electronics&Information Technology,2009,31(10):2392-2396. [6]柯召,孙琦.数论讲义[M].北京:高等教育出版社,2001. [7]Wang X Y,Yu H B,et al.Efficient collision search attacks on SHA-0 [C]//In Proc.the 25th Int.Cryptology Conf.(CRYPTO),2005:1-16 [8]Douglas R.Stinson.密码学原理与实践[M].3版.冯登国,译.北京:电子工业出版社,2009.1.3 计算 Diffie-Hellman问题(CDHP)[8]
1.4 判定 Diffie-Hellman问题(DDHP)[8]
2 新方案的实现
2.1 系统参数初始化
2.2 代理密钥对生成算法

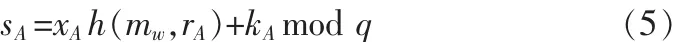
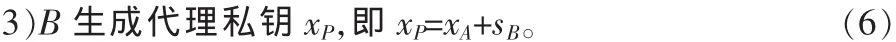
2.3 代理签名算法
2.4 代理签名验证算法
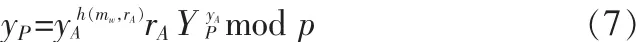
2.5 揭示代理者身份算法
3 方案的安全性分析
3.1 可验证性
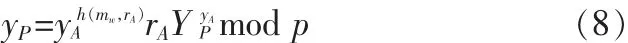

3.2 不可伪造性
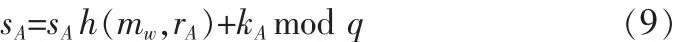

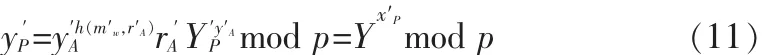
3.3 防止代理权滥用
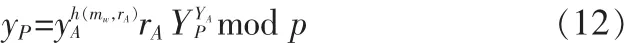
3.4 匿名性和身份确认

3.5 不可否认性
4 结束语

