上证综指Markov预测模型合理性卡方检验方法

李俊海， 周瑞芳

(河南工业大学 理学院， 河南 郑州 450001)

上证综指Markov预测模型合理性卡方检验方法

李俊海， 周瑞芳

(河南工业大学 理学院， 河南 郑州 450001)

在建立上证综合指数Markov预测模型过程中，连续型指数需转换为较少状态的离散时间序列。只有选择恰当离散化方法，才能保证所得离散时间序列满足马尔科夫性。借助同分布卡方检验方法，可检验给定两个出发状态的转移概率分布之间是否存在差异。若同一转移概率矩阵不同行的分布差异较大，表明两个出发状态确有差异，即这两行对应的状态划分合理。而不同历史时期转移概率矩阵同一行的比较，可作为检验马尔科夫链非齐次性的一种方法。

上证综合指数； 马尔科夫链； 卡方检验； 划分状态； 非齐次性

股票大盘指数反映股市综合变化趋势和波动程度，是股票市场运行状况的重要指标。投资者可利用大盘指数判断股市变动趋势，把握发展态势，选择相应投资策略。为预测股票市场大盘指数走势，国内外学者利用方差分析、回归分析、遗传算法、马尔科夫链等多种方法建立预测模型。由于马尔科夫链模型算法简单、可操作性强，逐渐成为该领域研究热点之一。李海涛[1]、陈增辉等[2]多个文献运用齐次马尔科夫链工具探讨了A股市场大盘指数涨跌趋势。胡淑兰等[3]建立隐马尔科夫模型讨论了股市在五种状态之间的变换规律。随着研究深入，非齐次马尔科夫链的作用逐渐得到重视。张兵[4]利用滚动样本方法与非齐次马尔科夫链研究了中国股市日历效应。马丹等[5]通过对比中国证券市场实际交易数据与模拟数据发现：动态马尔科夫状态转移模型克服了EKOP模型受买卖方数据影响而产生的系统偏误。然而，许伟河[6]指出，在使用马尔科夫链预测大盘指数的研究中，现有文献存在两个问题：一是，研究结论缺乏一致性和稳健性，即直接应用马尔科夫链模型预测某一时间段大盘指数变动，而不验证马尔科夫链预测模型是否有效；二是，大盘指数的状态设定与样本长度选择具有主观随意性。并针对第二个问题提出了基于滚动窗口的马尔科夫链预测模型，给出了该模型下最优窗口长度和状态阀值。该文未讨论状态阀值设置合理性检验方法，也没有涉足第一个问题的解决方法。有关马尔科夫链在上证指数预测方面的最新研究进展，有兴趣的读者可查阅文献[7]及其他参考文献。

为研究方便，文献[6]中两个问题可细化为：(1)直接使用非齐次马尔科夫链研究上证指数的规律，却忽视验证该工具的合理性；(2)人为定义模型的所有状态，缺少状态设置合理性检验。然而，这两个问题可以借助同分布卡方检验方法得以解决。

本文将遵循数据选取、状态划分、估计转移矩阵与检验等4个步骤讨论该问题。首先选择数据，由于交易制度与政策的巨大变化，有必要选取不同时期有代表性的三段数据，根据指数涨跌幅的波动性(标准差)，给出各离散状态所代表的指数取值区间，确定各时刻指数所对应的状态。其次，利用状态转移频数数据，分别估计三阶段的一步转移概率矩阵，通过考察同一转移概率矩阵不同行的分布相同与否，检验状态设置的合理性。最后，审查不同转移矩阵同一行之间的差异性，以验证马尔科夫链的非齐次性，为使用滚动样本方法奠定理论基础。

1 选择数据时间段

由于早期交易制度变换频繁，导致同一交易制度的数据较少，为此只考虑T+1交收制度下的数据。虽然股票市场于1995年1月已实行T+1交易制度，但交易者需适应一段时间才能形成交易习惯，有必要延后一段时间作为起点。2001年6月12日国务院发布文件启动国有股减持工作，7月24日江淮汽车、烽火通信等4家公司率先实施了国有股减持，导致上证综指不断下跌。只有1996年12月17日至2001年7月11日之间的上证综指无重大异常事件影响的迹象，运行特征反映了上证综指T+1交易制度下固有发展规律，可选为第一时间段。

2005年4月29日中国证监会启动股权分置改革试点工作。随着股改深入，股民热情逐渐高涨，2005年12月8日上证指数走出颓势，进入一段波澜壮阔的行情，2007年10月16日达到最高点6124。随后开始快速下跌，且后继震荡余波不断。直至2014年4月股改事件的影响才基本消失。为展现管权分置政策的主要影响，选取2005年12月8日至2014年4月30日为第二时间段。

2010年3月31日证监会开始接受券商融资融券交易申报，信用交易正式成为市场操作手段。朱民武[8]基于2010年3月31日至2012年底上证A股指数与融资融券余额交易数据，发现融资融券的推行并没有加剧A股市场的波动。随着多家券商融资融券门槛降低，2014年4月之后信用交易空前活跃，上证指数进入一个崭新阶段。为此2014年5月1日至2016年6月3日看作第三时间段，代表融资融券交易制度下的规律。

上证综指每日涨跌幅度是一个相对量，不受指数绝对大小的影响，使得不同时期指数具有可比性，选取这三段时间内每日的涨跌幅为原始数据。

2 涨跌幅度等级划分

股票市场投资者常用“涨”与“大涨”等语言，却没有明确划分标准。如果大涨的划分标准不恰当，将导致马尔科夫链各出发状态的转移概率分布几乎相同，失去研究价值。一般而言，如果数据波动幅度大，则超过较大阀值的改变才能称为“大”；若波动幅度小，阀值也应变小。通过计算可知，上证指数涨跌幅的标准差为1.69%，它反映了涨跌幅的波动程度。类似于正态分布“3σ原则”思想，涨跌幅在正负1.69%之间取值的可能性大约为70%，若超出这个范围规定为“大涨”(或“大跌”)比较合理。

基于上述阀值与涨跌性质，上证指数可分为大涨、上涨、下跌与大跌等4类，作为马尔科夫链的4个状态，并依次简记为数字1,2,3,4。

3 一步转移概率矩阵

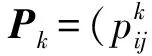
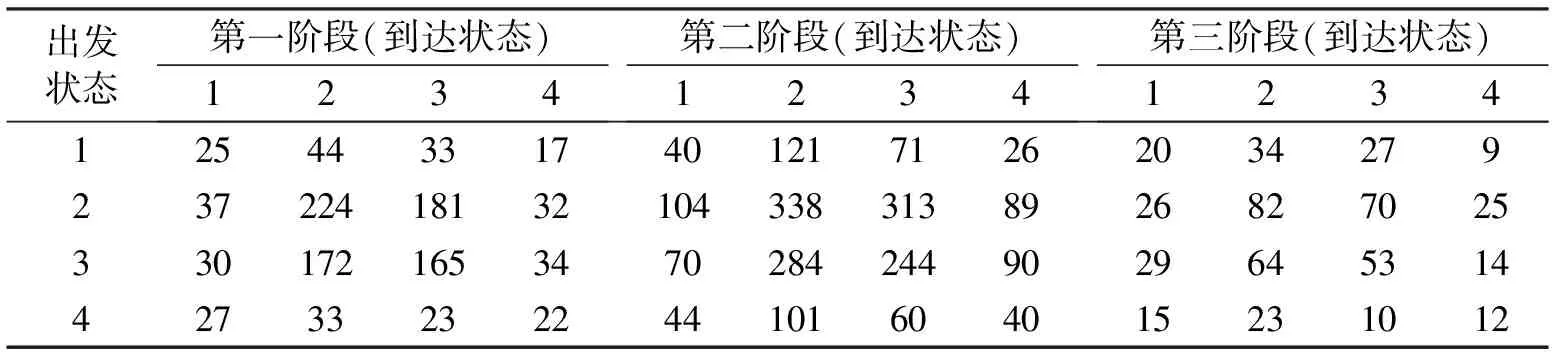
表1 各时间段状态段状态之间转移频数

各元素除以其所在行的行和，可得一步转移概率矩阵的估计：

4 状态划分合理性检验

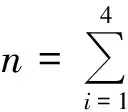
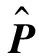
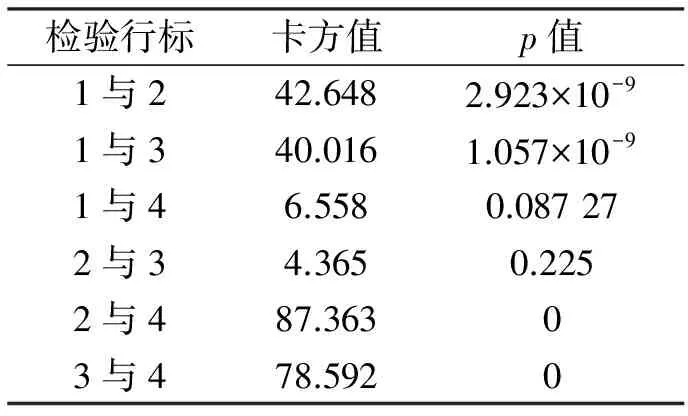
表2 第一阶段转移概率卡方检验

综合上述分析可知，状态划分比较合理。

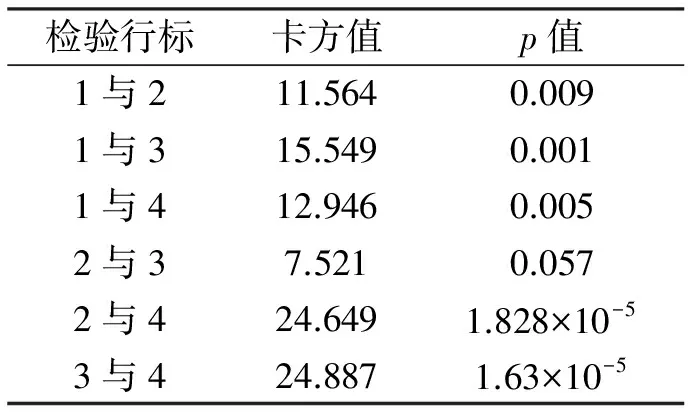
表3 第二阶段转移概率卡方检验

表4 第三阶段转移概率卡方检验

5 转移概率矩阵的动态性检验

这充分说明上证指数在不同历史阶段具有不同一步转移概率矩阵，即描述上证指数的马尔科夫链具有非齐次性，齐次马尔科夫链不再是合适工具。

6 结束语

本文通过比较不同出发状态的转移概率分布，利用卡方分布验证状态划分合理性。而不同历史时期转移概率矩阵同一行分布列的比较，验证了马尔科夫链的非齐次性。该方法不仅在股票指数分析中有效，也可用于其它领域。需要指出的是，在检验非齐次性时，只使用了同一行之间的比较。如果能同时考察两个转移概率矩阵所有对应行之间的差异之和，则检验效果更佳，希望统计理论深厚的读者进一步研究。

[1] 李海涛.运用马尔科夫预测法预测股票价格[J].统计与决策,2002(5):25-26.

[2] 陈增辉.基于马尔科夫链模型的沪综指数预测[J].金融经济,2008(14):58-59.

[3] 胡淑兰,魏捷,黄晟.基于HMM的中国股市状态转换及预测[J].统计与决策,2011(22):152-154.

[4] 张兵.中国股市日历效应研究：基于滚动样本检验的方法[J].金融研究,2005(7):33-44.

[5] 马丹,牛秀敏,王芳.中国证券市场知情交易概率的动态马尔科夫状态转移模型研究[J].数理统计与管理,2012,31(4):717-726.

[6] 许伟河.基于滚动窗口马尔科夫链预测模型的股票指数波动情况研究[J].上海金融学院学报,2014(6):67-75.

[7] 阎春宁,刘瑞辉,张欢欢.基于马尔可夫链改进股市的预测精度[J].统计与决策,2016(8):76-79.

[8] 朱民武.融资融券对股价的影响——基于沪市A股的经验研究[J].技术经济与管理研究,2014(11):95-99.

[责任编辑：张存凤]

Rationality verification of Markov model for composite index of Shanghai stock exchange by Chi-square test

LI Jun-hai, ZHOU Rui-fang

(College of Science, Henan University of Technology, Zhengzhou 450001, China)

In process of establishing Markov model to predict the Shanghai Composite Index, the continuous index must be converted to a discrete time series with few status. When the discrete method is suitably selected, it can guarantee that the obtained discrete time series satisfies the Markovian property. With the help of Chi-square test method, the difference between probability distribution for given two setting status can be tested by comparing corresponding rows of transition probability matrix. If there is more difference between two rows in same transition probability matrix, then one status can be distinguished from another, that is, two status corresponding to those rows are reasonable setting. Furthermore, by comparing same row of different transition probability matrix, a method is given to test the non-homogeneous of the Markov chain.

composite index of Shanghai stock exchange; Markov chain; Chi-square test; status setting; non-homogeneous

1673-2944(2017)01-0082-04

2016-09-01

2016-10-24

河南省高等学校重点科研项目(16A110011)；河南省教育厅科技学术基金资助项目(12B110003)

李俊海(1969—)，男，河南省邯郸市人，河南工业大学副教授，博士，主要研究方向为应用统计。

O211.62; F830.91，

A