一种有效的授权部分委托代理签名方案
杨育东, 张建中
(1.陕西师范大学 数学与信息科学学院, 陕西 西安 710062;2.陕西理工学院 数学与计算机科学学院, 陕西 汉中 723000)
0 引 言
1996年,Mambo等[1]提出了代理签名。一个代理签名方案,允许由原始签名者委托的代理签名者代表原始签名者给文件签名,而任何人都能验证其签名,这很好地解决了代理委托的问题。通常代理委托可分为4种类型:完全委托、部分委托、授权完全委托、授权部分委托。在这4种委托类型中,最后一种被认为是较好的选择,因为它综合了部分委托和授权委托的优点,并且确认授权和验证签名在同一个步骤中同时完成。
为了实际应用,如在线信用卡交易、合同签署等,代理签名方案通常需要满足以下基本性质[2]:不可否认性、不可伪造性。同时,随着代理签名方案应用的日益广泛,一些新的问题也逐渐暴露出来,例如代理签名者滥用职权[3]。因此,一个好的代理签名方案还需要能够有效地防止代理权滥用。
近几年来,椭圆曲线上的双线性对密码系统逐渐引起了密码学研究者的注意,有些研究者构建的基于双线性对的签名方案[4]解决了代理委托的问题,满足一些交易的安全性要求,已经得到了实际应用,如在线代理行为或合同签署。
综合考虑部分委托和授权委托的优点,本文采用授权部分委托来构建一个基于双线性对的代理签名方案。在该方案中,原始签名者可根据需要将自己的签名权有限度地委托给不同的代理签名者。方案满足不可伪造性,除被委托的代理签名者外的任何人,都不能在多项式时间内以不可忽略的概率伪造一个合法的代理签名;方案同时满足不可否认性,原始签名者不能否认他做出的委托,代理签名者也不能否认他代表原始签名者产生的签名;另外,方案采用授权部分委托来构建,能有效地防止代理权滥用。
该方案主要只涉及一个Hash函数运算和一个双线性对运算,尤其在代理委托过程中不涉及运算量大的双线性对运算,具有较高的计算效率,极有利于实际应用。在实际应用中,原始签名者可能需要把他的签名权委托给不同的代理签名者,在这种情况下,本文的方案具有最优的计算效率,对原始签名者来说是最优的选择之一。
1 预备知识
为便于读者阅读和理解,首先介绍本文所涉及到的一些基本知识,然后介绍方案的结构及正确性概念。
1.1 双线性映射
设(G1,+)和(G2,×)是两个q阶循环群,其中q为大素数。e:G1×G1→G2是一个双线性映射,满足以下性质:
(1)双线性性 ∀P,Q,R∈G1,e(P+Q,R)=e(P,R)e(Q,R),e(P,Q+R)=e(P,Q)e(P,R);
(2)非退化性 如果P是G1的生成元,则e(P,P)是G2的生成元;
(3)可计算性 ∀P,Q∈G1,存在一个有效的多项式时间算法来计算e(P,Q)。
1.2 方案的结构及正确性概念
一个代理签名方案主要有三个当事人:一个原始签名者、一个代理签名者和一个验证者。原始签名者通过发布授权文件把他的签名权委托给代理签名者,然后代理签名者能够代表原始签名者签名,最后验证者能够确认授权和验证签名。
若代理签名者能够代表原始签名者产生一个合法的代理签名,则这个代理签名方案是正确的。
2 代理签名方案
2.1 初始化
系统机构(SA)选择两个q阶循环群(G1,+)和(G2,×),其中q为大素数,且在G1和G2上的离散对数问题都是难解的。设P是G1的一个生成元,e:G1×G1→G2是一个双线性映射,h:{0,1}*×G1→Zq是一个安全的Hash函数。系统的公共参数为Params={G1,G2,q,P,e,h}。
每个用户Ui选择自己的私钥xi∈Zq,并计算相应的公钥Yi=xiP。
2.2 代理委托
原始签名者U0要把签名权委托给代理签名者Up,先制定含有原始签名者、代理签名者、委托权限及有效期等信息的授权文件mw。然后,原始签名者U0选择一个随机数r0∈Zq,计算
R0=r0P,μ=h(mw,R0),σ=x0+r0μ(modq),
并将(R0,σ,mw)发送给代理签名者Up。
代理签名者Up收到(R0,σ,mw)后,首先计算μ=h(mw,R0),然后验证等式σP=Y0+μR0是否成立,如果等式不能成立,则要求U0重新发送。
2.3 产生代理签名
为了代表原始签名者U0给一份文件m∈{0,1}*签名,代理签名者Up首先选择一个随机数rp∈Zq,然后计算
Rp=rpP,S=(h(m,Rp)+xp+σ)-1Rp,
则代理签名为(Rp,S,R0,mw,m)。
2.4 验 证
验证者先检查授权文件mw,核实代理签名者及代理签名的合法性,然后计算μ=h(mw,R0),并验证等式
e(h(m,Rp)P+Yp+Y0+μR0,S)=e(P,Rp)
是否成立,如果等式不成立,则拒绝承认此代理签名。
3 安全性分析和比较
3.1 安全性分析
本文的方案是正确的,且满足不可伪造性、不可否认性等安全性要求,同时还能够有效地防止代理权的滥用。
3.1.1 正确性
代理委托验证式
σP=(x0+μY0)P=x0P+μY0P=Y0+μR0。
代理签名验证式
e(h(m,Rp)P+Yp+Y0+μR0,S)=
e((h(m,Rp)+xp+σ)P,(h(m,Rp)+xp+σ)-1Rp)=e(P,Rp)。
3.1.2 不可伪造性
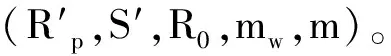
得到xp,则这是一个难解的离散对数问题。因此,原始签名者U0不能在多项式时间内,以不可忽略的概率伪造一个合法的代理签名。而其他人掌握的信息比U0还要少,因此也不能伪造一个合法的代理签名。于是,只有被委托的代理签名者才能产生合法的代理签名,即方案满足不可伪造性。
3.1.3 不可否认性
如果原始签名者U0不诚实,在代理委托阶段提供虚假信息,如计算μ时用的不是发布的授权文件mw,或者计算σ时不用自己的私钥x0,则它不能通过代理委托验证。而一旦U0把签名权委托给了代理签名者Up,因为最后只有用它的公钥Y0才能通过代理签名验证,所以原始签名者U0不能否认自己做出的代理委托。
同样,由于只有被委托的代理签名者才能产生合法的代理签名,因此,一旦原始签名者U0把签名权委托给了代理签名者Up,则代理签名者Up不能否认他代表原始签名者U0产生的签名。
3.1.4 防止代理权滥用
因为授权文件mw已经明确了原始签名者、代理签名者、授权权限范围以及授权期限等信息,所以验证者只要检查授权文件的内容就可以确定代理签名者是否合法以及是否在授权权限范围和授权期限内行事。一旦出现代理签名者假冒、逾越权限范围或者超过授权期限等问题,验证者可以当场宣布其代理签名的非法性。

3.2 方案比较

表1 双线性对运算次数的比较
本文的方案满足不可伪造性、不可否认性等安全性要求,并且能够有效地防止代理权滥用。与其它的代理签名方案[4-5]相比,本文的方案具有较高的计算效率,尤其在代理委托阶段不涉及运算量大的双线性对运算,极有利于实际应用。方案的比较结果如表1所示。
4 结 语
为便于实际应用,本文采用授权部分委托来构建基于双向性对的代理签名方案。方案满足一般代理签名方案需要满足的不可伪造性和不可否认性,并且能够有效的防止代理权滥用。
与其它代理签名方案相比,本文的方案具有较高的计算效率,尤其在代理委托阶段不涉及运算量大的双线性对运算,这极有利于实际应用。特别地,当原始签名者需要把签名权委托给多个代理签名者时,本文的方案是最优的选择之一。
[参考文献]
[1] MAMBO M,USUDA K,OKAMOTO E.Proxy signatures: delegation of the power to sign messages[J].IEICE Transactions on Fundamentals of Electronic Communications and Computer Science,1996,79(9):1338-1354.
[2] 樊睿,王彩芬,蓝才会,等.新的无证书的代理签名方案[J].计算机应用,2008,28(4):915-917.
[3] 张建中,魏春艳.一种新的无证书代理签名方案[J].计算机工程,2010,36(10):168-172.
[4] WANG Qin,CAO Zhen-fu.Efficient ID-based proxy signature and proxy signcryption from bilinear Pairings[C]//Computational Intelligence and Security.Berlin:Springer-Verlag,2005:167-172.
[5] 舒蕾,陈再兴.一种高效的基于身份的代理签名方案[J].软件导刊,2009,8(10):164-166.
[6] 王琴.一种基于身份的代理签密体制[J].计算机工程,2011,37(19):120-125.
[7] 刘树栋,梁向前,许金芳.安全有效的代理可验证加密签名方案[J].计算机工程与应用,2011,47(28):77-79.
[8] 王会歌,王彩芬,曹浩,等.基于离散对数的无证书代理签名方案[J].计算机工程与设计,2011,32(10):3284-3286.
[9] 邓胜国.基于身份无可信中心的签名体制研究[D].南宁:广西民族大学,2011.
[10] 刘雯.几类代理盲签名方案的研究[D].西安:陕西师范大学,2012.
[11] 吴磊,孔凡玉.一种高效的基于身份代理环签名方案[J].山东大学学报:理学版,2009,44(1):40-43.

