动态电路全部支路电流电压稳态演化规律

龙姝明， 冉启武， 董蓓蓓

(1.陕西理工学院 物理与电信工程学院， 陕西 汉中 723000；2.陕西理工学院 电气工程学院， 陕西 汉中 723003)

0 引 言

电器产品越人性化，电器设备的电路就越复杂。要计算出满足用户需求的电器设备电路元件参数，必须求出电路所有支路电流电压的演化规律，手工几乎是不可能快速解决这一问题的。编程列方程和解方程是行之有效的方法。

对于复杂多输入多输出动态电路，要得到全部支路电流电压演化规律，面临两个难题。一是列写时域方程比较困难，因为元件伏安关系不再是简单代数关系，支路电压与支路电流的关系可能是微分积分关系，不再是简单的一个输入一个输出的电路系统。因而列出的时域方程只能是微分积分方程组[1]，难以简化成一个高阶微分方程或一阶状态方程组。二是列出的微分积分方程组，在求解过程中必须面对手工无法解决的高次代数方程求根问题。解决上述第一个难题的有效方法是，用Laplace积分变换将时域动态电路问题转化为复频域(即Laplace变换的像域，又称为s域)的“像电路”问题[2]，再设计程序自动列写像电路节点电压方程或回路电流方程并解方程。解决上述第二个难题的唯一方法是，用软件(Mathematica，Maple，Matlab等)编程来分解高次代数多项式为多个简单因子的乘积，为求Laplace逆积分变换给出所有支路电流电压时域演化规律奠定基础。

自动列写复杂多输入多输出动态电路方程，快捷求解全部支路电流电压随时间演化的规律，直观表示各支路电流电压演化特性，用能量守恒来检验求解结果的正确性，用程序来实现这一目标，对于复杂动态电路而言，是一项有挑战性的工作。

1 拉普拉斯积分变换在动态电路求解中的作用

在我们研究的多输入多输出动态电路中，先假设：①时域信号源函数总可以用一组带单位阶跃函数因子的数学函数表示，并且这些函数在Laplace积分变换下的像函数很容易手工或编程求得；②电路所有动态元件积累的初始能量为零(只关注长时间后电路的稳态响应)；③电路中所有信号源都是内阻为零的理想电压源或内阻为无限大的理想电流源(如果内阻有限非零且已知，则可以将其归并到相应电阻元件中)。

取电感元件初始电流和电容元件初始电压为0，将电阻R、电容C、电感L时域电流电压约束关系(即伏安关系)取Laplace变换映射到像(s)域，则有表1第四列的s域伏安关系。

表1 电阻、电容、电感时域、像域伏安关系即像域电阻模型

比较元件时域与像域伏安关系发现，如果将电感和电容看成导纳分别为GL=1/(sL)和GC=sC的电导元件，那么时域动态电路在Laplace变换的像域(s域)中，可看成电阻电路(参见表1)。于是不再需要列写动态电路的时域微积分方程，只要列出各扩展支路像电压像电流满足的代数方程[3]，就可以解出全部支路的像电压像电流的s域函数。再取逆Laplace积分变换(也即依据黎曼梅林公式求留数和)就能给出全部支路的时域电压电流函数。

结论是，只要取Laplace积分变换，解复杂动态电路的问题就不再是难题。

2 s域扩展支路模型

节点电压分析方法中，不允许出现理想电压源支路。要允许电路中既有理想电流源又有理想电压 源存在，需要扩展像域支路的概念。我们在理想电压源支路中串入“虚拟小电阻r”(求出s域节点像电压后再取r趋近于零的极限，就可以消去r)，将一条单一元件支路扩展为三个元件组成的一条扩展支路，以便我们的求解程序可以处理有理想电压源支路的情况。我们的一条扩展支路是三个元件的有序组合，即一个理想电压源Us(s)串联一个导纳元件G(s)，再并联一个电流源Is(s)，扩展支路如图1，其中导纳元件可以是电阻、电容、电感，也可以是这三种元件的串、并联组合。

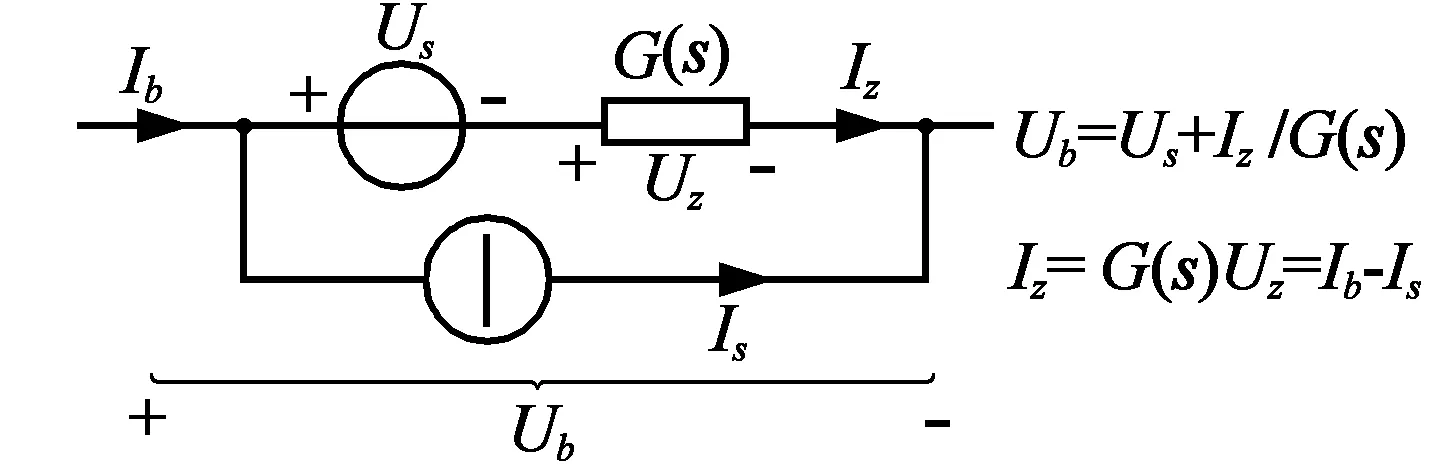
图1 复杂动态电路分析中 的s域扩展支路模型

设Us(s)=LT[us(t)]，Is(s)=LT[is(t)]分别表示对us(t)，is(t)取Laplace积分变换。约定实际支路与扩展支路的对应关系用表2描述。引入扩展支路模型，为编程自动列写复杂动态电路s域节点电压方程组做好了准备。

表2 实际元件支路与扩展支路模型参数对应关系

3 建立描述电路拓扑关系的重要矩阵

为了最大限度简化建立电路方程的过程，首要问题是电路拓扑关系和元件参数的输入与表示。这需要将电路扩展支路和独立节点有序化，即分别编号索引。方便的做法是,给每个扩展支路设一个电流流向,选支路电流流入端为支路电压的“+”端，流出端为支路电压的“-”端。这样选择的结果是电路中所有元件消耗的功率总和为零(即能量守恒)，信号源消耗功率小于0时，表示信号源为电路提供大于0的功率。

3.1 输入时域电压源矢量usv[t]和电流源矢量isv[t]

约定支路电流流入电压源的“+”端时，电压源电压取正，否则，电压源电压取负。约定电流源电流与支路电流流向一致时，电流源电流取正，否则，电流源电流取负。由电流源和电压源函数乘正负号来构成时域电压源矢量usv[t]和电流源矢量isv[t]。再取Laplace变换，给出s域电压源矢量Usv和电流源矢量Isv。

3.2 输入电路元件参数及拓扑关系表示矩阵EPTR

设我们所要求解的电路有n个节点，k条扩展支路。要最大限度降低表示、输入电路元件参数、拓扑关系的难度，可以先将电路的k条扩展支路编号为1到k，将n个节点编号为1到n，连接支路最多的节点赋以最大节点编号n。以扩展支路为单元输入电路元件参数、信号源像电流Is(s)、像电压Us(s)及电路拓扑关系信息。设所要研究求解的电路元件参数及拓扑关系表示矩阵为EPTR(Element Parameters and Topology Relations)。规定EPTR矩阵有k行6列，第j行的6个元素{bj，intoj，outj，Gj，Usj，Isj}描述第j条扩展支路的元件参数、电压源和电流源s域像函数及其与其它支路的拓扑关系。b表示扩展支路编号，into和out分别表示扩展支路电流流入端节点和流出端节点的编号，G表示扩展支路的等效像导纳，Us表示扩展支路电压源s域像电压函数，Is表示扩展支路电流源s域像电流函数(若Us或Is为负值，表示该支路中电压源极性或电流源电流方向与参考方向相反)。EPTR矩阵可表示为

(1)

按照上述规定对电路有序化，列出EPTR矩阵后，就可以方便地将电路元件相关参数和电路拓扑关系清楚地采集并列写出来，为后续的计算机编程提供方便。

3.3 建立拓扑关系矩阵

运行程序：

Aa=ConstantArray[0,{n,k}];

For[j=1,j<=k, j++, i=EPTR[[j,2]];Aa[[i, j]]=1;q=EPTR[[j,3]];Aa[[q, j]]=-1];

A=Take[Aa,n-1];

可由EPTR矩阵快速求出拓扑关系矩阵A，矩阵A有n-1行(分别表示n-1个独立节点)k列(表示k条支路)。矩阵A描述了每条扩展支路关联的电流流入节点(用1表示)和电流流出节点(用-1表示)。

3.4 建立电路电导矩阵Gm

用节点电压法列写电路方程时，要知道每个节点的自电导和互电导，因此建立节点电压方程时必须列写n-1行n-1列的电导矩阵Gm，它的主对角线元素是各独立节点的自电导，非主对角元素是独立节点间的互电导，互电导带负号。我们先建立b行b列的对角电导矩阵Gdm，它的主对角线元素对应每条支路的等效电导，非对角元素均为零。再用矩阵公式

AT=Transpose[A]，Gm=A·Gdm·AT，

(2)

求出Gm矩阵，其中AT是A的转置矩阵。从EPTR中自动求出Gm矩阵的程序为：

Gd=ConstantArray[0,{n,k}]；

For[j=1, j<=k, j++,Gdm[[j, j]]=EPTR[[j，4]]]; Gm=A·Gdm·AT。

3.5 节点的s域电流源矢量Isv

在s域中，流入每一支路的电流源可以集合为一个电流源矢量Isv，每一支路的电压源可以集合为一个电压源矢量Usv。运行程序：

Isv=EPTR[[All,6]];Usv=EPTR[[All,5]];

可以求出Usv及Isv。或者，对usv[t]和isv[t]取Laplace积分变换给出Usv和Isv。再通过支路电导对角矩阵Gdm和电路拓扑关系矩阵A，可解得流入每个节点的总像电流源矢量：

Insv=A·(Gdm·Usv-Isv)。

(3)

3.6 仅有理想电压源元件的支路索引矩阵ivsm

必须记录单独的理想电压源构成的支路，为求单独理想电压源支路的电流和电压提供必要的信息。记录格式为：

ivsm={{单独理想电压源支路编号，电流流入端节点号},…}。

运行程序：

ivsb=Position[EPTR,1/r][[All,1]]; Livsm=Length[ivsb]; ivsm={};

For[j=1, j<=Livsm, j++, jb=ivsb[[j]];AppendTo[ivsm,{jb,EPTR[jb,2]]}]]。

可由EPTR自动建立ivsm矩阵。

4 复杂动态电路节点像电压方程的列写和求解

复杂动态电路节点电压法是以独立节点像电压作为未知函数，将各独立节点像电压函数集合为矢量Unv，应用基尔霍夫电流、电压定律和扩展支路伏安关系，可以给出复杂动态电路关于n-1个独立节点的节点电压方程组：

Gm·Unv=Insv。

(4)

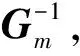
(5)

利用电路拓扑关系矩阵解出支路像电压矢量Ubv：

Ubv=AT·Unv。

(6)

利用扩展支路电路模型，分别解出支路电导元件两端的像电压矢量Uzv、支路电导元件中的电流矢量Izv、支路像电流矢量Ibv：

Uzv=Ubv-Usv,Izv=Gdm·Uzv，Ibv=Izv+Isv。

(7)

由单电压源支路索引矩阵ivsm，依据节点电流定律，可以导出单电压源支路像电流，所需程序为：

For[j=1, j<=Length[ivsm], j++,ib=ivsm[[j,1]];ic=isvm[[j,2]];cin=Drop[Range[1,k],ib];

Ibv[[ib]]=-A[[ic,ib]]*Sum[A[[ic,p]]*Ibv[[p]],{p,cin}]]。

电导元件消耗(包括电容、电感存储)的总功率必定等于所有电源供给的总功率，即有

p(t)=izv(t)uzv(t)+izv(t)usv(t)+isv(t)ubv(t)=ibv(t)ubv(t)=0。

(8)

5 复杂动态电路全部支路电流电压演化规律求解程序设计

依据前面的讨论，我们可以调用Mathematica强大的符号矩阵和数值矩阵运算功能，设计出Mathematica程序：对电路中所有信号源函数取Laplace变换、列写复杂多输入多输出动态电路s域节点电压方程、解出所有支路像电流像电压函数、对支路像电压像电流函数取逆Laplace变换给出全部支路电流电压随时间变化的规律。难解决的任务都由计算机系统来完成。特别注意，单个理想电压源支路串入待定电阻r，适当时间再令r趋于0，是利用节点电压法解有理想电压源支路的复杂电路的技巧之一。

基于以上分析，我们编写的Mathematica程序主要部分如下：

k=电路支路总数；n=电路总的节点数；T=信号源周期；

EPTR={{b1,into1,out1,G1,Us1,Is1},{b2,into2,out2,G2,Us2,Is2},……,{bk,intok,outk,Gk,Usk,Isk}}

ivsb=Position[EPTR,1/r][[All,1]];Livsm=Length[ivsb];ivsm={};

For[j=1, j<=Livsm, j++, jb=ivsb[[j]];AppendTo[ivsm,{jb,EPTR[[jb,2]]}]]

Aa=ConstantArray[0,{n,k}];

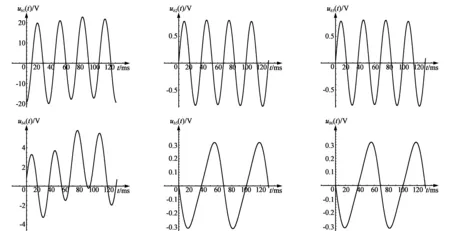
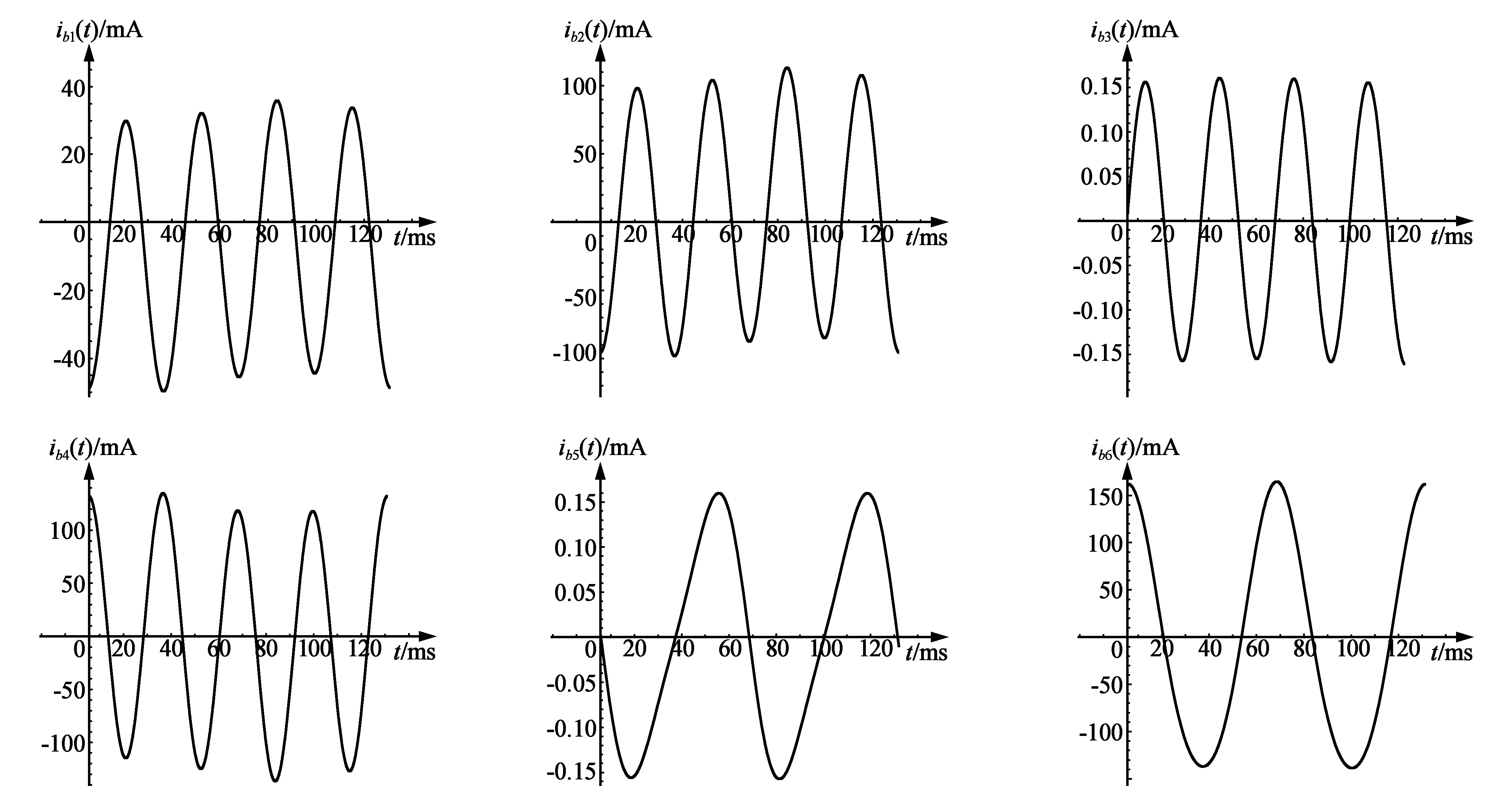
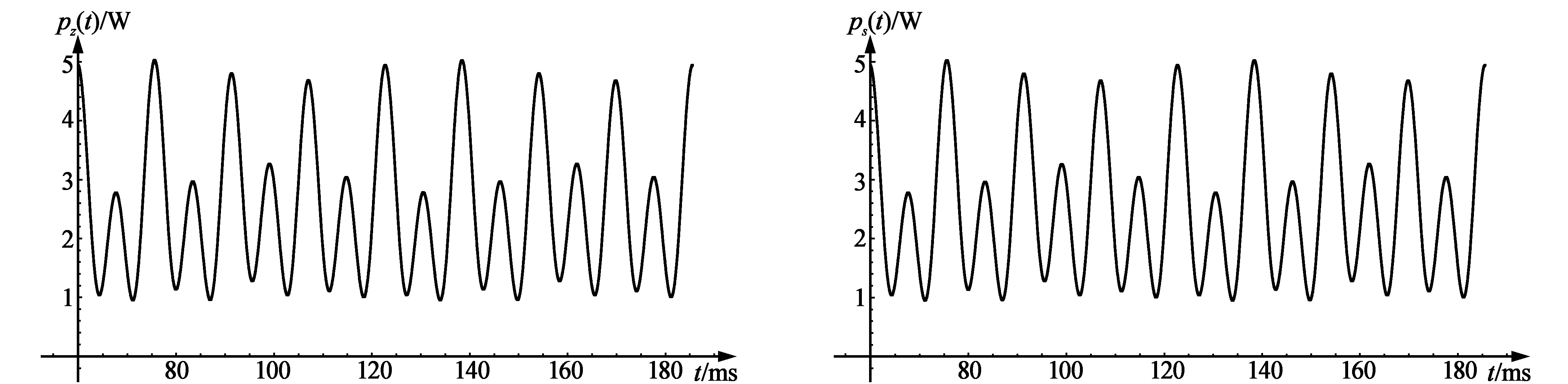
For[j=1,j

A=Take[Aa,n-1];Clear[Aa] (n-1行k列电路拓扑关系矩阵);

Usv=EPTR[[All,5]] (Usv是支路电压源矢量);

Isv=EPTR[[All,6]] (Isv是支路电流源矢量);

Gdm=DiagonalMatrix[EPTR[[All,4]]] (Gdm是对角电导矩阵);

AT=Transpose[A] (AT是电路拓扑关系矩阵A的转置);

Insv=A.(Gdm.Usv-Isv) (Insv是流入每个节点的电流源矢量);

Gm=A.Gdm.AT (Gm是电路节点电压方程电导矩阵);

IG=Inverse[Gm] (IG是节点电压方程电导矩阵Gm的逆矩阵);

Unv=Limit[IG.Insv,r->0] (Unv是节点电压矢量);

Ubv=AT.Unv (Ubv是支路电压矢量);

For[j=1,j<=Livsm, j++,qb=ivsm[[j,1]];Ubv[[qb]]=Usv[[qb]]];

Uzv=Ubv-Usv (Uzv是电导元件的电压矢量);

Ibv=Gdm.Uzv+Isv (Ibv是支路电流像函数矢量);

For[j=1, j<=Livsm, j++,ib=ivsm[[j,1]];ic=ivsm[[j,2]];cin=Drop[Range[1,k],ib];

Ibv[[ib]]=-A[[ic,ib]] (A[[ic,cin]].Ibv[[cin]])] (计算理想电压源支路电流);

Izv=Ibv-Isv (Izv是电导元件电流矢量);

unv[t_]=InverseLaplaceTransform[Unv,s,t] (时域节点电压矢量函数);

ubv[t_]=AT.unv[t] (ubv是时域支路电压函数);

ibv[t_]=InverseLaplaceTransform[Ibv,s,t] (ibv是时域支路电流矢量函数);

t1=T;t2=4T;

Table[Plot[ubv[t][[q]],{t,t1,t2},PlotRange->All],{q,1,k}] (支路电压波形);

Table[Plot[ibv[t][[q]],{t,t1,t2},PlotRange->All],{q,1,k}] (支路电流波形);

usv[t_]=InverseLaplaceTransform[Usv,s,t];isv[t_]=InverseLaplaceTransform[Isv,s,t];

uzv[t_]=ubv[t]-usv[t];izv[t_]=ibv[t]-isv[t] (uzv，izv是电导元件的时域电压、电流矢量函数);

p∑[t_]=ibv[t].ubv[t] (时域各支路总功率函数，其值应该为0)。

6 复杂动态电路求解实例

通过求解16个元件、13条支路、6个节点、2个电压源、2个电流源构成的多输入多输出复杂动态电路(见图2)，展示我们提出的电路解法思想和程序的用法。约定图中支路参考电流的流入端是各支路电压的“+”端。电路的索引已经标于图中。

图2 16个元件、13条扩展支路、6个节点的多输入多输出复杂动态电路，b=13，n=6

描述4个信号源的程序语句为：

ε[t_]=UnitStep[t];is1[t_]=0.01ε[t];is4[t_]=0.02Cos[100t]ε[t];

us7[t_]=15Cos[200t]ε[t];us12[t_]=20Cos[400t]ε[t];T=π/200。

特别在理想电压源支路中加入虚拟电阻R7=r，于是各支路元件参数分别为：

{R1,L2,R3,c4,R5,L6,R7,R8,c9,c10,R11,L12,R13}=

{500,0.02,5 000,10-4,2 000,0.01,r,100,10-5,10-6,200,0.02,4 000}。

由图2见，扩展支路数k=13,节点数n=6。特别注意，支路1上的电流源流向与支路1的电流参考流向相反，支路12上参考电流是从电压源“-”端流入的，因此，电路的电流源矢量isv(t)和电压源矢量usv(t)为：

isv[t_]={-is1[t],0,0,is4[t],0,0,0,0,0,0,0,0,0};

usv[t_]={0,0,0,0,0,0,us7[t],0,0,0,0,-us12[t],0}。

参考图2，得到电路元件参数及拓扑关系表示矩阵EPTR：

EPTR={ {1,1,6,1/R1,0,Isv[[1]]},{2,2,6,1/(s×L2),0,0},{3,2,6,1/R3,0,0},

{4,3,6,s×c4,0,Isv[[4]]},{5,4,6,1/R5,0,0},{6,4,6,1/(s×L6),0,0},

{7,5,6,1/R7,Usv[[7]],0},{8,4,5,1/R8,0,0},{9,3,4,s×c9,0,0},

{10,2,3,s×c10,0,0},{11,1,2,1/R11,0,0},

{12,1,3,1/(s×L12),Usv[[12]],0},{13,3,5,1/R13,0,0}}。

运行程序后得到的拓扑关系矩阵为：

A={ {1,0,0,0,0,0,0,0,0,0,1,1,0},{0,1,1,0,0,0,0,0,0,1,-1,0,0},

{0,0,0,1,0,0,0,0,1,-1,0,-1,1},{0,0,0,0,1,1,0,1,-1,0,0,0,0},

{0,0,0,0,0,0,1,-1,0,0,0,0,-1}}；

ivsm={{7,5}}。

运行程序给出电路中支路1—6在时域[π/200,4π/200]上的电压电流函数波形(图3和图4)。

图3 在图2电路支路1—6的电压函数时域波形

图4 在图2电路中支路1—6的电流函数时域波形

原电路总的消耗和存储功率pz(t)的波形和电源提供的总功率ps(t)的波形见图5，两个波形完全相同，电路能量时时守恒。

(a)总的消耗和存储的功率波形 (b)信号源提供的总功率波形图5 原电路总的消耗和存储的功率波形和电源提供的总功率波形

7 结 语

通过用Mathematica程序分析方法可以快速解决复杂系统的动态电路求解问题，并且可以直观形象地以图像的形式展现其中电流电压随时间变化的关系。这为生产及科学研究工作中相关问题的探讨提供了一种有效的解决途径。

[参考文献]

[1] 王斌,王迎飞,龙姝明.动态电路计算机解法研究[J].中国新技术新产品,2009(1):10-11.

[2] 张志良.用等效阻抗法解暂态过程[J].浙江师大学报:自然科学版,2001,24(3):314-316.

[3] 付奎,杨俊海,王风华,等.大规模实时电路程序分析方法[J].陕西理工学院学报:自然科学版,2010,26(3):13-17.

[4] 龙姝明,朱杰武,孙彦清,等.数学物理方法& Mathematica[M].西安:陕西人民教育出版社,2002:343-367.