精心设计数学题组 培养学生迁移能力

（闽侯竹岐中学，福建 闽侯 350107）

精心设计数学题组 培养学生迁移能力

兰孝辉

（闽侯竹岐中学，福建 闽侯 350107）

题组教学是数学教学的常用方法，也是引导学生的认知走向深入的有效途径。题组教学对于理清新、旧知识间的关系，实现旧知向新知的迁移及提高解题能力有明显的助力。一法多用、一题多变、背景衍生、比较递进等方式不仅能起到由例及类、新旧结合、纵横类比、固本拓新的作用，还能提高学生举一反三的能力。

教学设计；数学题组；迁移能力

教育的价值除了传授知识和技能，更重要的是要让学生学会学习，发展学生能力，尤其是迁移能力。美国学者埃德加·富尔在《学会学习》一书中指出：“未来的文盲不再是不识字的人，而是没有学会学习的人。”可见，培养和促进学生的学习迁移能力，注重培养方式和策略的研究，具有重要的现实意义。

题组教学是数学教学的常用方法，也是引导学生的认知走向深入的有效途径，符合循序渐进和量力性原则。题组教学对于理清新、旧知识间的联系与区别，实现旧知向新知的迁移及提高解题能力有明显的效果。因此，精心设计的题组教学，不仅要促进学生对知识由零散、杂乱到系统、有序的迁移，而且要促使学生由机械记忆、死记硬背等静态型思维向善于分析、综合、应用等动态思维的迁移，最终实现学习能力的提高。文章就如何结合课堂教学、课内外练习，精心设计数学题组，实现学生迁移能力的提高。

一、设置一法多用的比较题组，培养学生深刻掌握思想方法的迁移能力

数学命题形式是多种多样，千变万化的，但在解决问题中，常常是通过联想迁移、运用类比，化归等思想方法，将陌生的复杂问题转化为已熟知的简单问题。因此，教师在教学过程中可对学生难以理解掌握的疑难问题，一法多用，精心设计成题组加以训练。

2.已知：（x+1）2+（x+y+1）2=0，求2x+y的值。

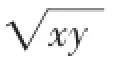
本题组从命题的角度发散，涵盖初中代数中数、式、方程有关知识，解法角度相对集中，通过以上同一类问题的不同图式与不同条件的题组训练，可使学生在比较中学会归纳，学会类比，达到举一反三、触类旁通的效果。

二、设置递进题组，培养学生新、旧知识的迁移能力

建构主义理论认为，学习的过程是学习者主动建构的过程。数学知识连续性很强，旧知与新知间有着密切的联系，教学中可以设置递进题组引导学生在原有的知识结构的基础上学习新的内容，实现旧知向新知的迁移，促进学生良好知识结构的形成，提高学生习得知识的迁移范围。

如，在圆周角定理教学之后，学习圆内接四边形的对角互补性质，可设置如下题组引入新课。

1.如图1，点A、B、C三点在圆O上，若∠A=50°，求∠BOC的度数。

2.如图1，在1的基础上，若点D是圆O上异于A、B、C的任意一点，你能运用圆周角定理，求出∠D的度数吗？

3.若∠A改为n°，1、2题中其他条件不变，∠D的度数是多少？

4.通过以上探索，你发现∠A与∠D存在怎样的数量关系？试用文字语言加以叙述。

本课例从学生现有的最近发展区出发，以寻找特例作为问题情境教学的切入点，通过已知与未知之间的联想类比，引导学生探索新知，发展理性思维能力。由于题组中问题的提出是循序渐进、步步拓宽的，因此教学过程的推进符合学生的认识规律，有助于学生在新旧知识的联系中，提高迁移能力。

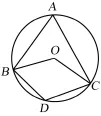
图1

三、现实生活衍生题组，促进学生从实践向理论的迁移

学生在课堂所学的基础知识，只有应用于生产、生活实践，分析和解释社会现象，才能实现学习的积极、正向迁移，促进能力的形成。因此教师要善于创造时机和空间，引导学生联系实际应用知识。在完成课堂基础知识、基本技能和基本方法教学的同时，创设系列问题情境，让学生将实际问题化归为数学问题加以解决，适当时机下还可以引导学生主动提出问题、解决问题，使学生的“感性迁移体验”通过多角度的应用教学上升为“理性体验”，促进在实现“从理论到实践”的基础上，完成“从实践向理论”的迁移。因此，教学中教师可设计由现实生活背景衍生出的一连串环环相扣、由浅入深的系列问题，引导学生积极探索。

A、B两地相距100千米。甲车从A地出发，速度为60千米/小时；乙车从B地出发，速度为40千米/小时。

1.两车同时出发，相向而行，问几小时两车相遇？

2.若乙车先出发10分钟后，甲车与乙车相向而行，问几小时相遇？

3.两车同时出发，相向而行，问几小时两车相距36千米？

4.两车同时出发，同向而行，乙车在前，甲车在后，问几小时甲车追上乙车？

5.两车同时出发，同向而行，乙车在前，甲车在后，问几小时两车相距36千米？

6.请你利用题中已知条件设计一个问题，与你的同桌交流解题过程。

第1—3题主要训练学生总结出相向而行的等量关系：甲车行驶路程加上乙车行驶路程等于全程。第4、5题则训练学生总结出同向而行的等量关系：甲车行驶路程减去乙车行驶路程等于全程。其中第2、4题涉及分类讨论。第6题则设计为开放性问题，让学生提出问题，分析问题，并解决问题，在探索中学会合作。

本题组涵盖了行程问题中相遇与追及问题。教学中还可以引伸到环行跑道相遇与追及问题和时针与分针转动规律问题。如：从某天的下午1点到3点，是否存在时针与分针的重合、夹角为直角、平角，若存在，试求出相应的时间；若不存在，请说明理由等问题。在多种问题情境中教会学生对知识的应用与变通。

四、设置比较、递进的综合题组，培养学生探究、拓广的迁移能力

在教学中，多角度变换命题，精心设计比较、递进的综合题组，既有助于解题方法、规律的归纳，又能揭示潜在于题组中的特殊情景，培养学生的探究迁移的能力，克服干扰。

1.如图2，在Rt△ABC中，∠BAC=90°，AB=AC，MN是过点A的直线，CD⊥MN于D，BE⊥MN于E。

（1）求证：BE=AD；

（2）若CD=2，BE=3，求DE的长；

（3）试说明DE、BE、CD之间有何数量关系，并证明你的结论。

2.如图3，在Rt△ABC中，∠BAC=90°，AB=AC，MN是过点A的直线，CD⊥MN于D，BE⊥MN于E.

（1）求证BE=AD；

（2）若CD=2，BE=3，求DE的长；

（3）试说明DE、BE、CD之间有何数量关系，并证明你的结论。

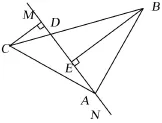
图2

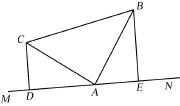
图3

3.如图4，∠AOB=90°，OA=OB，若点B的坐标为（3，1），求点A的坐标。

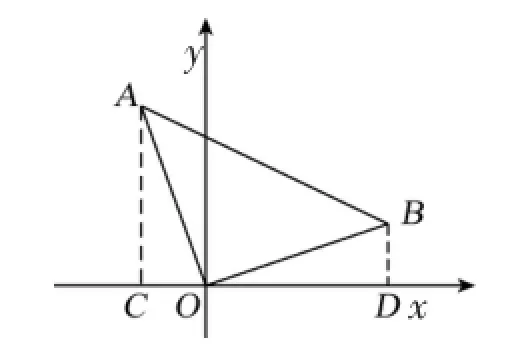
图4

4.如图5，等腰梯形ABCD中，AD∥BC，∠B=45°， P是BC边上一点，△PAD的面积为，设AB=x，AD =y

（1）求y与x的函数关系式；

（2）若∠APD=45°，当y=0时，求PB·PC的值；

（3）若∠APD=90°，求y的最小值。

（本题为2013年福州市毕业升学考试第21题压轴题）

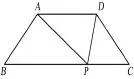
图5

这是一个比较、递进综合题组，第2题是第1题直线MN绕着直角顶点旋转得到；第3题在第1、2题的基础上进一步深化，拓展到平面直角坐标系中加以研究；第4题是在第2题的基础上，由全等深化拓展延伸到K字型相似，通过以上题组的探索，达到解一题、通一类。在这类变式训练中，教师还可有意设置一些看似形同，解题方法却完全迥异的题型供学生训练。这种形同质异习题，对学生求异思维培养大有裨益，能有效提高学生分析问题、解决问题的能力，在更高的层面上提升知识、方法的迁移层次。在复习阶段加强这类题组的对比训练，更能提高课堂的实效性。

总之，问题是数学的心脏，迁移是问题解决的核心，题组教学能起到由例及类、新旧结合、纵横类比（对比）、固本拓新的作用。因此，我们教师要精心研究课本的例、习题，选择具有迁移效应的问题变式系列引导学生自主探究，从而促进学生数学迁移能力的提高。

［1］汪凤炎,燕良轼.教育心理学新编［M］.广州：暨南大学出版社，2006：290-301.

［2］教师资格认定考试编写组.教育心理学［M］.北京：北京师范大学出版社，2008：98-104.

［3］康培坚.浅谈数学课堂中问题情境的创设［J］.福建中学数学，2002（5）.

［4］中考命题组.2013年福建省福州市中考数学试卷及答案（Word解析版）［EB/OL］.［2013-07-19］. http://www.12999.com/html2/9888.html.

G633.6

A

1673-9884（2017）02-0064-03

2016-12-24

兰孝辉，男，闽侯竹岐中学一级教师。