基于课堂教学改革下活动单的教学——“导数在研究函数中的应用”教学案例

☉江苏省白蒲高级中学 潘丹丹

基于课堂教学改革下活动单的教学
——“导数在研究函数中的应用”教学案例

☉江苏省白蒲高级中学 潘丹丹

函数是高中的核心内容，学习函数时，我们分别研究了函数的三要素、函数的单调性、函数的奇偶性、函数的图像、函数与方程、函数与不等式等内容，并且从数与形两个方面进行了研究.通过在高二的新知学习，我们充分利用导数研究了函数的单调性、极值、最值等问题，这就是本节课我们所研究的内容——导数在研究函数中的应用.

首先看基础自测：

活动一、基础自测

2.函数y=x+2sinx在区间［0，π］内的极大值是___________，最小值是___________.

3.设（fx）=4x3+mx2+（m-3）x+n（m，n∈R）是R上的单调增函数，则实数m的取值范围为___________.

4.已知函数f（x）=ex-2x+a有零点，则a的取值范围是___________.

5.函数f（x）的定义域为R，f（-1）=2，对任意x∈R，f′（x）＞2，则f（x）＞2x+4的解集为___________.

处理方式：以小组为单位，多屏展示答案，学生思考知识点及方法.上课后投影，学生回答简要过程、方法及知识依据.

通过学生的主动回答，教师与学生共同梳理知识点.

要点梳理：（板书）

导数：

1.函数的单调性

f′（x）＞0⇒f（x）单调递增；

f′（x）＜0⇒f（x）单调递减.

f（x）在区间A上单调递增⇒f′（x）≥0在区间A上恒成立；

f（x）在区间A上单调递减⇒f′（x）≤0在区间A上恒成立.

2.函数的极值和最值

求导，令f′（x）=0，列表.

3.函数的零点，不等式恒成立问题

将问题转化为函数的最值问题.

通过课堂的教学，学生能在基础自测中提出自己的想法，例如第4题，学生讲解时提出了直接研究和参变分离的想法，学生在第5题提出构造新函数g（x）=f（x）-2x在R上单调递增时，立刻有学生补充提出可以特殊化处理，例如构造函数f（x）=3x+5，充分展现了学生思维的发散性.

设计意图：从知识层次出发，通过基础自测让学生在知识层面上认识利用导数研究函数的单调性，函数的极值、最值，函数的零点问题，不等式恒成立问题，而这些问题都以函数单调性的研究为中心，进而提出如何利用导数把握函数的单调性呢？并引入活动二.

活动二、典型例题

处理方式：学生投影并简述过程及方法.（学生提出补充，质疑，让学生进行总结提炼）

生1：解：定义域为（0，+∞），

（1）当a-4≤0，即-2≤a≤2时，f′（x）＞0，则f（x）的单调递增区间为（0，+∞），无单调递减区间.

（2）当a2-4＞0，即a＞2或a＜-2.

①若a＜-2时，则f（x）的单调递增区间为（0，+∞），无单调递减区间.

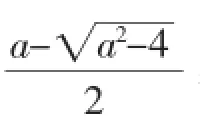
则f（x）的单调递增区间为（0，x1）和（x2，+∞），单调递减区间为（x1，x2）.

综上可知，当a≤2时，f（x）的单调递增区间为（0，+∞），无单调递减区间；

当a＞2时，f（x）的单调递增区间为（0，x1）和（x2，+∞），单调递减区间为（x1，x2）.

（学生自我总结）

总结：本题在研究函数单调性时，方式是通过求导判断导函数f′（x）的符号，其本质是判断二次函数在（0， +∞）上的符号，首先考虑它的根“定”与“不定”，“定”指的是能因式分解，“不定”则依据判别式进行讨论，分Δ≤0和Δ＞0两种情况研究，然后抓住二次函数的图像利用数形结合的思想方法研究根是否在定义域内.

同时在黑板上画出导函数的图像，并让学生提出质疑与想法：

当a≤2时，f（x）的单调递增区间为（0，+∞），无单调递减区间；

当a＞2时，f（x）的单调递增区间为（0，x1）和（x2，+∞），单调递减区间为（x1，x2）.

在利用导函数图像判断导数符号后，提出思考：

思考1：如果定义域变为（1，+∞），结合图像如何认识函数的单调性呢？

学生遇到的困惑就是如何解决导函数的根与（1，+∞）的关系，结合图像，发现f′（1）=2-a.当a＞2时，f′（1）=2-a＜0，所以x1＜1＜x2，从而得出结论：

当a≤2时，f（x）的单调递增区间为（1，+∞），无单调递减区间；

当a＞2时，f（x）的单调递增区间为（x2，+∞），单调递减区间为（1，x2）.

刚才求导后通过抓基本初等函数的图像来加以判断导函数的符号，还有其他的形式吗？

在此题的基础上看变式1.

h′（x）＞0，得x＞1；h′（x）＜0，得0＜x＜1，所以h（x）的单调减区间为（0，1），单调递增区间为（1，+∞），所以h（x）在x=1取得极小值，也是最小值.h（x）min=h（1）=3＞0，则g′（x）＞0.

所以g（x）的单调增区间为（0，+∞），无单调递减区间.

总结：通过对刚才的问题分析，我们可以体会到在利用导数研究函数单调性时常常研究的方式有：

（1）在基本初等函数的基础上抓其图像，利用数形结合的思想方法进而研究；

（2）非基本初等函数下通过两次求导进一步研究函数.

给学生1分钟时间自主梳理，提出思考2.

思考2：在基本初等函数图像的基础上利用导数研究了函数的单调性，那你能画出原函数的大致图像吗？（学生上黑板）

学生画图时遇到的问题是：当a＞2时，图像与x轴的交点，通过学生的思考与认知，学生能主动发现（f1）=-a＜0，而（fx）在（1，x2）上单调递减，所以（fx2）＜0，进而得到原函数的大致图像，同时让学生体会到画图像时的注意点是对大致走势、渐近线、特殊点的把握.

在此基础上看变式2.

处理方式：在变式1的基础上充分利用导函数与原函数的图像研究，学生将其解题思路展示在黑板上.而学生解决时遇到的困难有分类讨论的层次以及在计算上存在问题，充分利用函数的图像加以分类讨论进而得到解决.过程如下：

解：当a≤2时，（fx）在［1，2］上单调递增，

minmax

当a＞2时，

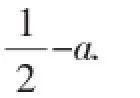
minmaxln2+2-2a；

min0max2a.

在此基础上，请进一步探究：

通过对上述变式的研究，结合函数的图像可知，

本题除了这种方法之外，还可以从参变分离的角度研究：

设计意图：活动二从思维层次出发，利用例题研究函数的单调性，解决如何利用导数把握函数的单调性，从局部和整体角度，充分利用了基本初等函数的图像.在此基础上，并通过对定义域的改变和变式1再次体会如何利用导数研究函数的单调性，进而总结出从基本初等函数的图像和两次求导两种方式进行研究函数的单调性.在单调性的基础上提出思考2，让学生画出原函数的大致图像，在此基础上进一步引出变式2和变式3，体现出思维层次的递进性.

本节课利用导数研究了函数的单调性、极值、最值，围绕函数的单调性、极值、最值借此研究了方程有解问题，实际上围绕函数的单调性、极值、最值还可以研究不等式的恒成立问题或证明不等式问题，这个问题我们留着后面再研究.