一道高考题的解法引发的教学思考

☉江苏省南通市天星湖中学 成倩文

一道高考题的解法引发的教学思考

☉江苏省南通市天星湖中学 成倩文

平面向量是高中数学课本中的一个重要内容，与诸多内容广泛联系，错综复杂.向量兼备代数与几何双重形式，是解决数学问题的重要工具，其中最精彩的当属“向量的数量积”，这也是历年高考中的必考内容.本文就以2016年高考江苏卷第13题为例，谈谈笔者对此题的分析以及一些常见解法和特殊解法，再借助新颖特例强化向量的数量积的基本方法，最后再回归到平时的课堂教学过程中，进一步完善教学方法.

一、分析高考题，赏析多种解法

图1

对于向量的数量积问题，一要掌握数量积的定义及数量积的公式，二要理解数量积的几何意义，三要熟练数量积的坐标运算公式，四要会借助一组基底灵活“拆”、“分”一个向量.而本题没有（或不易求出）所求向量的长度，所以只能利用向量坐标法和基底法解决问题了.具体方法如下：

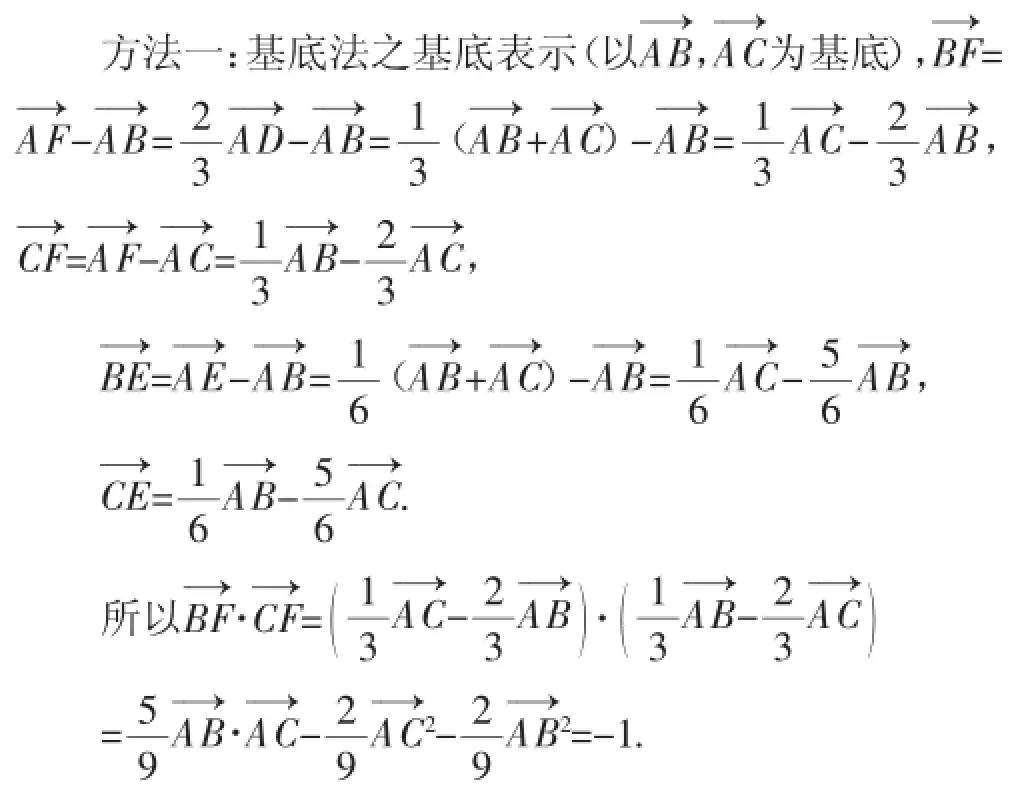
评注：同样是基底法，方法一比较常见，选择一组基底表示向量，则整个问题相当于转化为这两个未知数（基底），较为简便地解决了问题.方法二则比较新颖，更换基底并用新的基底表示，再把向量都化为这组基底，体现了逆用思想.

方法四：建系之特殊化（△ABC视为等腰三角形）.

由题意知，点B，C关于点D对称，故可令AB=AC，即△ABC为等腰三角形，以BC边所在直线为x轴，BC边的中垂线所在直线为y轴建立平面直角坐标系，设C（a，0），B（-a，0），A（0，b），则=（a，b）·（-a，b）=b2-a2=4.

评注：同样是建系，这种方法却很优越.对于填空题而言，特殊化是最简洁、最快捷、最有效的方法，同时也是学生最喜欢、最乐于接受的一种“懒惰”方法.

方法五：中间结论法（极化恒等式）.评注：此方法利用向量的极化恒等式：a·b=（a+

b）2-（a-b）2］，它来源于苏教版必修4课本P81习题2.4第5题的变式，几何意义是向量的数量积可以表示为以这组向量为邻边的平行四边形的“和的对角线”与“差的对角线”的差的，在三角形中，它可以用三角形的中线表示：a·b=它揭示了三角形的中线与边长的关系.很多这方面的试题用此法解决更快捷，更准确！

二、结合新题型，加强基本方法

图2

此题也是向量的数量积问题，同样不能利用数量积的定义和几何意义解题，只能利用基本方法：坐标法和基底法.不过本题坐标法对于基础薄弱的同学就一时难以想到，相对于能力稍强些的同学更容易联想到，也更容易操作一些，而基底法则更难以想到，对灵活运用知识解决问题的能力要求高一些.

方法一（坐标法）：以A为原点，过点A且与直线m，n平行的直线为x轴建立平面直角坐标系，则A（0，0），B（a，-1），C（b，-3），所以=（a+b，-4），

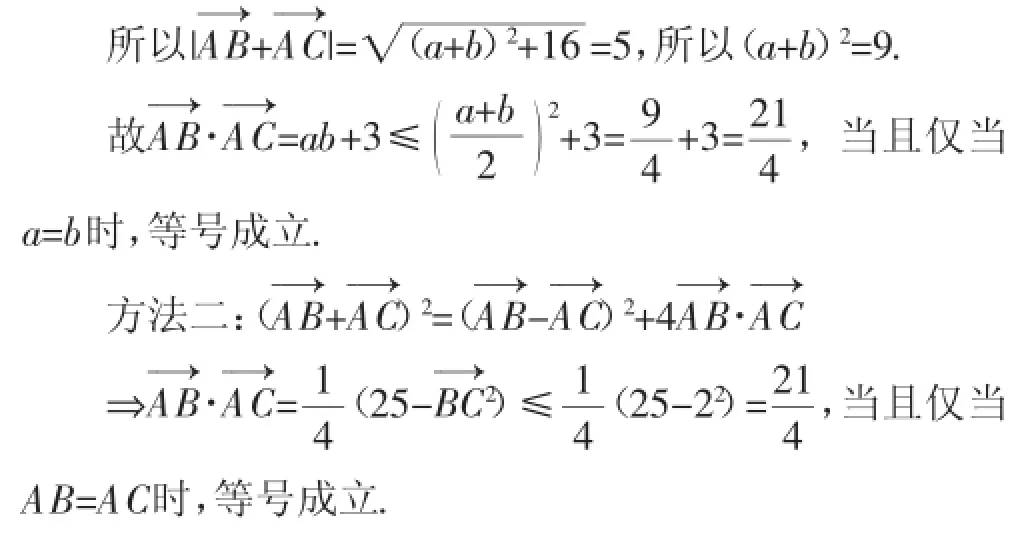
以上两题均主要考查了向量数量积的基本方法：坐标法和基底法.也有一些题会考查平面向量的数量积的定义和几何意义，但作为高考题，向量题如果放在第10题之前，则可能偏向于考查向量的基本定义、向量基本坐标运算和模的运算，比如2015年江苏卷则将向量放置在第6题，就只考查了向量坐标之间的运算；若向量题放置在第10题之后，相比来说更需要学生能够灵活分析，将向量间的知识综合运用起来.

三、研究新课程，优化课堂教学

鉴于此，在以后平面向量知识的教学方面，教师除了要将向量基本定义和运算让学生熟练化，更需要引导、启发学生寻找题中的关键词，构建向量模型，利用基底法和坐标法来解决问题.在复习阶段，教师在加强向量基本知识训练的同时，更要突出向量与其他知识交汇处的复习，从而使学生面对新颖灵活题型时，“临危不乱”，能够迅速分析问题，正确解决问题.为此，加强有效课堂教学势在必行，可从以下三个环节入手：

1.联系实际生活，创设问题情境，激活学生主动学习的兴趣

向量是现代数学中的一个新生内容，学生比较生疏，难以理解.所以在向量这个课堂导入环节，教师要结合教学内容和学生的实际情况，多费心思，创设问题情境激发学生的问题意识；充分准备，提升学生自主参与课堂探究问题的意识.

2.小组讨论学习，培养合作精神，加深学生对知识的理解与运用

向量题型灵活，必须及时掌握、巩固与练习，它们是下一步学习顺利开展的基础.教师提出问题，小组展开讨论，先由各位组长根据题目讲解思路，其余三人进行回答或补充.这样一方面有利于发展学生交流、表达和思辨能力；另一方面有利于营造宽松、民主、和谐的教学氛围，促使学生互相学习、互相帮助，体验集体荣誉感和成就感，发展合作精神.让学生积极参与课堂，自主理解和掌握新授知识，能举一反三.

3.例题立于基础，由易到难，培养学生思维的灵活性和发散性

备好课才能上好课，老师在选取知识应用方面的例题时，先以教材中提供的例题为基础，然后再根据课标的要求以及新知识的推广，进行适当变式，由易到难的变化引导学生进行发散性思维的培养，尽可能地出现一题多解，并引导学生分析各种方法之间的优劣，提高学生解题能力的同时，引导学生对解题过程进行精炼和简化，提高解题效率，培养其创造性思维.

总之，教师一定要抓住新课程下的三维目标进行优化教学，组织和设计合理的课堂导入，激发学生的学习兴趣；通过深入浅出的问题链，激发学生的求知欲，强调学习过程的重要性；丰富讨论形式，增强生生互动，创设好的学习氛围；积极备好课，选好例题，以少胜多，重在学生的主体参与和师生互动.