浅谈高三一轮练习讲评课中数学核心概念的有效培养

☉浙江省天台中学 余飞宏

浅谈高三一轮练习讲评课中数学核心概念的有效培养

☉浙江省天台中学 余飞宏

数学概念是人脑对现实对象的数量关系和空间形式的本质特征的一种反应形式，是掌握数学基础知识和提升运算能力、发展逻辑推理能力和空间想象能力的前提.从一定程度上讲，学生学习知识主要是从客观事实完成个体特征抽象出概念，再通过对概念的应用加深理解客观事物之间的联系.数学核心概念是指在整个高中数学学习过程中起到一个统领、主导作用的概念，也是学生提升数学学习力的关键所在，是高中数学学习的奠基石.因此，核心概念的学习就显得至关重要.高三一轮复习是学生提升概念的理解，形成学生数学核心素养的一个关键时期.但我们的日常教学中，大部分时间沦为简单的罗列知识点和大量重复习题的练习，并没有从深层次挖掘数学概念的内涵，这样复习达到的效果往往是学生对于数学概念的理解层次较浅，不能抓住核心概念，往往导致遇到“生题”无从下手，对数学核心素养的提升起不到任何效果.只有抓住核心概念这一解决问题的根本，学生在解决问题时才能将问题进行转化，从而达到提升核心素养的效果.下面笔者在高三一轮练习讲评课中，就如何引导学生从核心概念入手，思考和解决数学问题，进而使学生在解决问题的过程中提高数学思维能力，提升数学核心素养.

一、问题引导，挖掘概念内涵

高中数学课程标准指出：“数学教学中应加强对基本概念和基本思想的理解和掌握，对一些核心概念和基本思想要贯穿高中数学教学的始终，帮助学生逐步加深理解.”抽象化和形式化是数学概念的基本特征，在练习讲评时可以尝试以问题引领，将具体的数学问题与抽象的概念结合来深化学生对数学本质的认识，围绕着问题所涉及的数学核心概念，巧设问，妙追问，来深化学生对数学核心概念的理解.

问题1存在函数f（x）满足：对于任意x∈R都有（）.

A.f（sin2x）=sinxB.f（sin2x）=x2+x

C.f（x2+1）=|x+1|D.f（x2+2x）=|x+1|

很多同学在求解时无从下手.教师在讲评时引导学生关注题中提到的“存在函数”一词，尤其是“函数”两个字，启发学生去深入挖掘函数概念的本质.通过问题指引的方式引导学生思考：

（1）函数的概念是什么？

（2）自变量x与函数值f（x）之间存在着怎样的对应关系？

（3）这些函数的图像有什么特征？

（4）怎样的对应关系才是真正意义上的函数，你能得出什么结论？

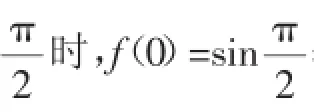
二、逆向思考，深化概念外延

任何一个概念都有内涵和外延两个方面，概念的内涵是指概念所反映对象的特性和本质属性，而概念的外延是概念所反映对象的具体范围.要掌握一个概念，必须要准确把握这个概念的确切含义和所指的对象范围，而概念外延恰恰是概念应用的生长点，也是考查学生对数学概念理解的关键.

问题2在正方体ABCDA1B1C1D1中，E是棱CC1的中点，F是侧面BCC1B1内的动点，且A1F∥平面D1AE，则A1F与平面BCC1B1所成角的正切值构成的集合是__________.

图1

（1）根据所学知识，怎样才能得到线面平行？

（2）怎样理解“随着F点的运动，始终有A1F∥平面D1AE”？

（3）过一个定点A1能作出无数条直线与平面D1AE平行，你能得到什么结论？

（4）F点在运动的过程中，它的轨迹又是怎样的？

（5）如何作出这两个平面的交线？

本题正是抓住线面平行这一概念的外延，逐步推进，探求本源，解决问题.在分析解决问题的过程中，通过师生互动，展示学生的思维心路历程，逐渐暴露学生的知识上的思维断点，引导学生主动思考，这样的讲评不仅拓展了学生的解题思路，更加训练了学生的逆向思维.使学生能够举一反三，在解决类似问题时学会逆向思考的思维方式，深化对概念外延的理解.

三、思维展示，关注多元表征

高中生对数学概念脉络的表征情况可以分为三类，第一类为知识点比较零散，知识之间的联系断裂，基本方法掌握较差，尚未形成体系；第二类为能对已学知识点形成体系，但基本是停留在书本层面，基本方法掌握较好，针对问题选择方法的能力较差；第三类不仅有较为完善的知识体系，而且知识面宽，拓展能力强，基本方法掌握很好，针对具体问题选择恰当方法的能力也很好.多元表征水平较好的学生中能够形成较好的数学概念脉络，较差的学生其概念脉络不成体系；数学本身强调文字语言、图形语言与符号语言之间的转化.数学概念特别是数学核心概念，更是要通过多种形式进行表达.在核心概念的理解方面要注重选取多元素材，激发多元思考，引发多元联系.通过多远表征深化概念的理解与应用.

向量具有代数的严谨和几何的直观，有着“数”与“形”的双重身份，平面向量的数量积是平面向量部分的核心概念，而且与三角、立体几何等知识也有交汇.向量数量积的概念，有两种形式：一种形式是a·b=|a||b|cos＜a，b＞，它的几何意义是|a|与b在a方向上的投影|b|cos＜a，b＞的乘积，另一种是坐标形式a·b=x1x2+y1y2.以上是平面向量数量积这一概念的不同表征.在讲评这道练习时让学生展示自己的解题思路，展现不同的思维方式.

思路1：利用基底的意识.

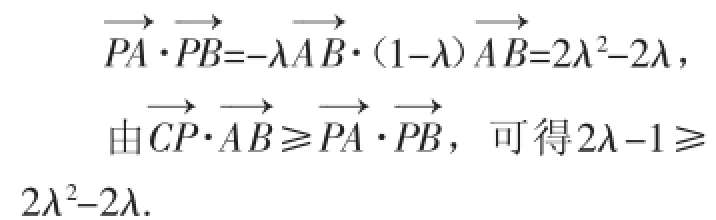
又因为P在AB边上，

所以0≤λ≤1，

思路2：利用向量的投影意识.

0

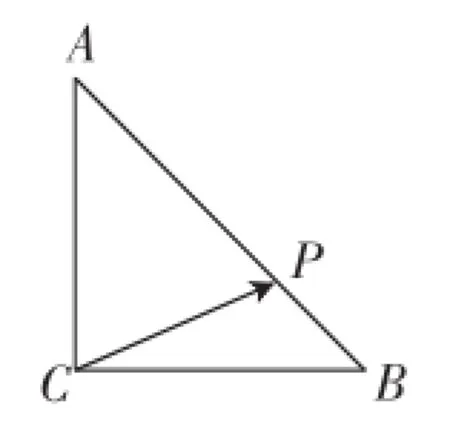
图2

图3

（2）P在线段P0A上，即0≤λ≤（*）时，在上的投影为-|，此时

图4

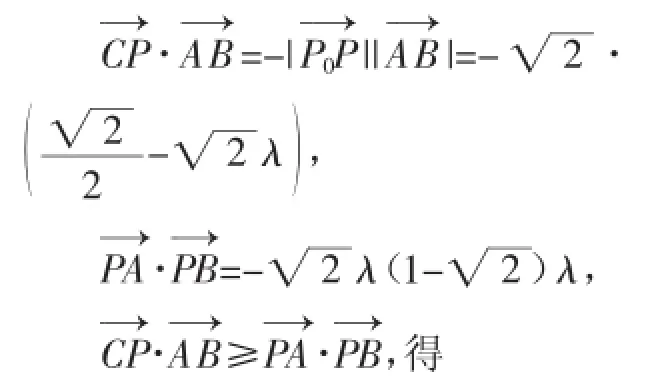
思路3：利用坐标意识，以C为原点建立平面直角坐标系，可知A（1，0），B（0，1），P（λ，1-λ），

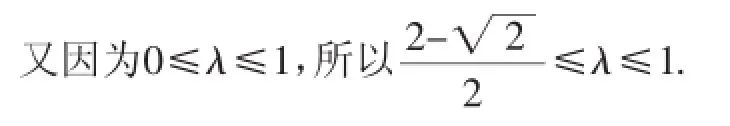
在学生介绍完自己的解题思路，教师适时讲评，引导学生总结思考数量积的每一种形式，适用于什么条件；利用基底意识、坐标意识与投影意识解决向量问题又有什么区别.

进行练习讲评时，如果在此基础上能从不同角度去理解、感悟概念，并在讲评之后加以归纳总结，相信会更有助于学生对核心概念知识的体系化.

四、科学评价，深化理解概念

数学概念的理解是一个逐步深化的过程，教师在课堂上通过练习针对性的讲评可以深化学生对概念的理解，但是在整个教学过程不仅包含教师的“教”、学生的“学”，还有一个重要环节：通过相关的针对性练习反馈，对学生的掌握情况进行“评”.教师的教，促使学生对问题与概念的理解；学生的学，加深学生对概念的感悟；但只有通过具体的操作才能进一步提升学生的思维，形成数学素养.

我们在以上例题讲解的基础上不妨配合相应练习，提升学生对概念的理解与感悟.

例如，在问题3讲评好之后可以在课堂上或课后做相关的练习.

练习1在▱ABCD中，已知AB=2，AD=1，∠DAC=60°，点M为AB的中点，点P在BC与CD上运动（包括端点），则的取值范围是__________.

图5

回归教材，回归数学核心概念，突出能力立意，是当今数学高考命题的方向.我们要在练习讲评课中渗透对数学核心概念的讲解，重视提炼数学核心概念的教育价值，培养学生从概念出发去思考、从概念出发来解决问题的习惯.教师只有在平时的数学教学过程中充分关注数学核心概念的渗透，才能逐步加深学生对数学核心概念的理解和把握，进而使学生在学习解决问题的过程中提高解决和分析问题的能力，提升数学核心素养.

1.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013（5）.

2.方石.数学教学诠释思维品质［J］.数学通讯，2014（4）.

3.柴贤亭.数学教学中的函数问题设计［J］.教学与管理，2012（10）.

4.鲍建生.数学概念教学研究两例［J］.数学教学，2014（11）.