让“元问题”创设在思维发展主线上——例谈初中数学自主变式探究的问题设计

☉浙江湖州市南浔区教育教学研究和培训中心 姜晓翔

让“元问题”创设在思维发展主线上
——例谈初中数学自主变式探究的问题设计

☉浙江湖州市南浔区教育教学研究和培训中心 姜晓翔

一、问题缘起

当前，初中数学教学中，还是存在教学资源单一，教学结构僵化，以及教师在教学过程中本本主义倾向严重等问题，导致教师教得乏味，学生学得无趣，教学气氛不够活跃、教学效率低下等现象.波利亚曾说：“学习任何知识的最佳途径是由自己去发现，因为这种发现理解最深，也最容易掌握其中的规律、性质和联系.”基于上述认识，笔者认为，教终究是为学服务的，初中数学教学改革也必须从学生的立场出发，努力使他们焕发出生命力、学习力和发展力，让他们真正成为学习的主人，主宰学习过程.笔者曾在《合理创设元问题自主变式探生成》一文中结合一个教学案例分析了“元问题”在初中数学教学中如何激发并激活学生的思维，引导学生经历通过自主变式探究活动而最终提炼、掌握并体悟数学知识的过程.何谓“元问题”呢？在学生已有知识经验的基础上，教师根据教学内容的特点提出的能提高学生的求知欲并能激发学生发现和提出问题的问题称之为元问题.近段时间，笔者又多次通过教学研讨活动进一步实践并验证了元问题教学策略对于初中数学教学改革所起到的积极作用.数学教学是思维活动的教学，而思维又起源于问题.本文就以学生的思维发展为主线，结合教学案例来阐述如何在不同的思维发展节点处通过元问题的合理创设来激发学生的自主学习能力，从而提高学生的学习力和发展力.

二、元问题的创设策略

1.让元问题创设在思维孕育时，激发思维萌生点.

课的伊始，大多数学生还未能真正快速进入学习状态，这时，就需要教师通过元问题的创设来帮助学生孕育思维.期间，需要切准学生的认知困惑点和疑难处，才能有意识、有针对性地进行教学，从而快速地让学生的思维和所学内容交织在一起，成功激发思维萌生点.

【案例1】在浙教版八上“直角三角形复习”课堂教学开始阶段，授课教师是这样设计的.

元问题1：如图1，在△ABC中添加一个条件________，使得△ABC为直角三角形.

元问题2：如图2，若CD是Rt△ABC斜边上的高线，其中BC=1，你能再添加一个条件后设计一个问题，并解决你所设计的问题吗？

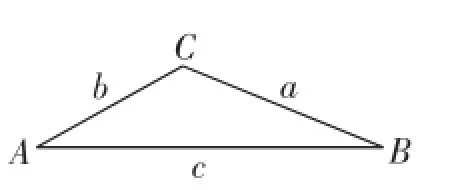
图1

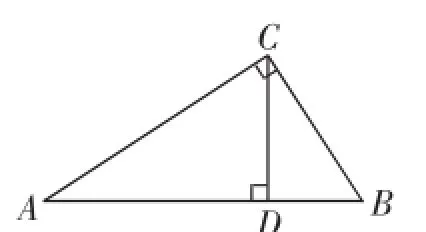
图2

【评析】授课教师在“直角三角形复习”课的开始阶段精心创设了两个非常巧妙的元问题.元问题1在结合具体问题的基础上有效激发了学生对于直角三角形判定的回顾.元问题2更是激发学生利用所学知识编题，学生可以通过添加一个边的条件或一个锐角的条件来设计出简单的直角三角形计算问题.教师在引导、组织学生编题和解答的过程中，不仅灵活地回顾了直角三角形的有关知识，而且能切准学生对于直角三角形这一知识点存在的困惑和疑难，以便让接下来的教学更有针对性.元问题的合理创设在起到孕育思维的效果的同时，成功激发出思维萌生点.

2.让元问题创设在思维发展时，抓住思维生长点.

当学生已进入学习状态，并对所学内容有了一定的认识，同时，教师对学情也有了进一步的认知时，需要让学生的学习思维进一步发展并生长.此时，教师创设的元问题所引发的自主变式探究可以帮助学生实现思维的发展，有效抓住学生思维的生长点.

【案例2】在浙教版七下“3.1同底数幂乘方（2）”课堂教学的例1及巩固练习之后，授课教师是这样设计的.

元问题：请同学们运用同底数幂的乘法、乘方等知识，在下面的算式的括号内任意填写一个关于m的代数式，编出一个算式，然后考考其他同学！

（）4+（）·m2+（）3.

【评析】本节课的教学内容主要是同底数幂的乘方，在解决了课本中例1及几个简单的巩固练习之后，授课教师正确地判断出学生的思维已顺利发展，并需要及时巩固及生长，因此创设了如此的元问题.该元问题有效起到了让学生对于同底数幂乘方运算的及时巩固的效果，抓住了思维生长点.

【案例3】在浙教版八上“一次函数中的面积问题”复习课中，在解决了一个基础的例题教学之后的教学片段如下所示.

元问题：如图3，已知函数y=kx＋b的图像经过点A（4，0），且满足____①，

____②.

请你编题：请在①处添一个条件，在②处提出一个问题，并解答.

生1：①：与y轴的交点B的坐标为（0，4），②：求该函数的解析式.

生2：①：与y轴的交点B的坐标为（0，2），②：求△AOB的面积.

生3：①：与y轴的交点为点B，△AOB的面积是8，②：求点B的坐标.

生4：①：与y轴的交点为点B，△AOB的面积是4，②：求该一次函数的解析式.

......

【评析】本节课主要是针对一次函数图像中面积问题的一节专题复习课，重点解决直线与坐标轴所围成的面积问题的计算.案例中元问题创设的时机恰到好处，正值学生已初步感知了“已知直线和点求三角形面积”及“已知点和三角形面积求直线的解析式”顺、逆两类问题之时.通过该元问题的创设，让学生经历主动提出问题和互相解答问题的自主变式探究过程，有效起到了发展思维、巩固知识点及抓住生长点的作用.

3.让元问题创设在思维生长时，寻求思维延伸点.

在学生经历了思维孕育、产生并发展时，会不由自主地进行思维的进一步生长.此时，教师如果能够及时通过有效元问题的创设，来促使学生的思维生长，就能寻求思维延伸点，起到关联横向与纵向知识点的效果，真正达到知识的融会贯通.

【案例4】在浙教版八下“6.1反比例函数（2）”例1之后的教学片段如下所示.

例1已知y是关于x的反比例函数，当x=3时，y=-6，求y关于x的函数解析式和自变量x的取值范围.条件1：已知y是关于x的反比例函数；条件2：当x=3时，y=-6.

元问题：能否改变例1中的某一条件，设计出属于你

的题目，并完成解答过程.

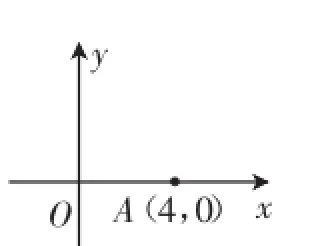
图3

生1：条件1改为：已知y是关于x的正比例函数.

生2：条件2改为：当x=2时，y=3.

生3：条件1改为：已知y是关于x-1的反比例函数.

生4：条件1改为：已知y是关于x2的反比例函数.

......

师：同学们都编得很好！老师也来编一个，将条件1和条件2同时改为：（如表1）

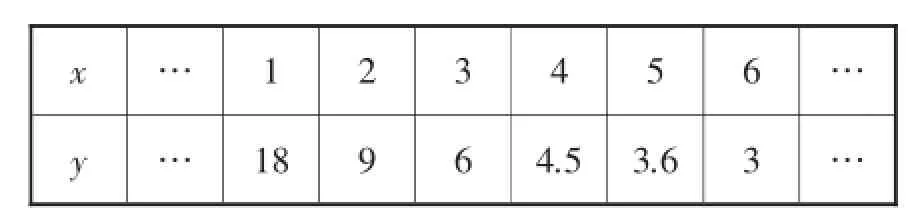
表1

【评析】本节课主要内容是用待定系数法求反比例函数的解析式.在解决例1及归纳了一般步骤之后，教师创设了这样的元问题，通过引导学生编题和教师补充编题的过程，自然地将例1分别从横向（不同函数类型）和纵向（对应数值不同表现形式）进行了适当拓展.几乎把所有类型的用待定系数法求反比例函数解析式的问题都覆盖到，并且大多数是由学生提出并互相解决的，让学生在思维生长时对问题有了更深层次的理解.在寻求思维延伸点的过程中，起到对某一知识点融会贯通的效果.

4.让元问题创设在思维拓展时，追求思维发散点.

到了这个阶段，学生的学习思维已较为成熟，经历了孕育、发展和生长，有时需要更进一步的拓展才能让学生的学习能力得到进一步提升.在具体的课堂教学中，往往可以通过元问题的创设来引导学生对所学知识自主从不同角度、不同背景、不同层面进行延伸与拓展，从而追求思维发散点.

【案例5】在浙教版八下“正方形中的动点问题探究”复习课中，前半段经历了简单的单动点和双动点的问题探究，接下来的教学片段如下.

如图4，在边长为4cm的正方形ABCD中，现有一动点P，现从A出发，以2cm/s的速度沿边经A-B-C-D到达点D.另有一动点Q，以1cm/s的速度从D出发，沿正方形的边按顺时针方向运动，相遇后同时停止，连接AP、PQ、QA.

元问题：根据以上信息，你能设计出一个怎样的问题？

（温馨提示：同学们可以从以下几个方面去思考：（1）线段的关系；（2）三角形形状；（3）面积问题……）

生1：t为何值时，点P与点Q相遇？

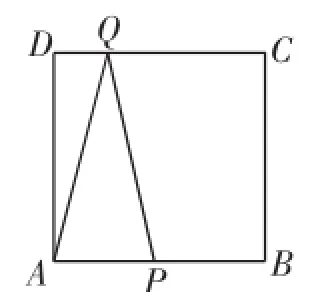
图4

生2：t为何值时，△APQ是等腰三角形？

生3：t为何值时，△APQ是直角三角形？

生4：设△APQ的面积为S，求S关于t的函数解析式.当t为何值时，S最大？最大值是多少？

......

【评析】本节课重点解决正方形中的动点问题的探究，包括单动点和双动点.上述片段是在授课教师引导学生解决了5个较为简单、基础的小问题作思维铺垫之后，设计的元问题，旨在引导学生自主提出在正方形背景下的典型问题，包括特殊三角形形状问题、面积问题等，让学生在提出问题、分析问题和解决问题的过程中思维充分拓展，而且是向不同角度、不同背景、不同层面进行延伸与拓展，追求思维发散点.

5.让元问题创设在思维整理时，找准思维回归点.

当学生通过学习活动得到了比较丰富的经验，且对经验有了自己独特的体验后，教师需要及时启发学生做好举三反一的工作——思维整理.没有思维整理的环节，这些学习经验都只是一条一条的、成散乱状态存在的.而经过思维整理，就可以将其融合、凝练，达成有序思维.元问题的创设可以有效引导学生自主进行思维的整理，找到问题的本源，挖掘问题的本质，从而找准思维回归点.

【案例6】在浙教版九上“3.3垂径定理（1）”课堂教学的最后阶段，教学片段如下所示.

先解决课本中的例2：一条排水管的截面如图5所示.排水管的半径OB=10，水面宽AB=16，求截面圆心O到水面的距离OC.

师：如果把线段OC向两边延长，与圆相交，如图6，我们还能求图中的哪些线段？

（学生能轻松解决该问题）

元问题：图6中，是否有可能，知道其中的两条线段（所有的半径或直径算一条），也能像我们刚才那样，能求出其他所有线段呢？

请同学们自己来尝试编题，编好后向全班同学展示并共同解答.

生1：已知OC=3，OE=5，求其他所有线段.

生2：已知OC=3，OB=5，求其他所有线段.

生3：已知OC=6，AC=8，求其他所有线段.

图5

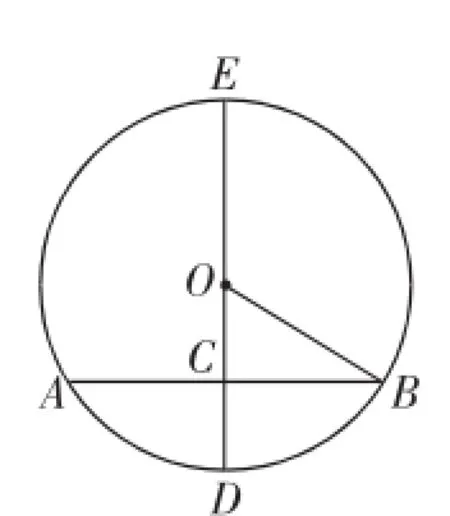
图6

生4：已知OC=6，BC=8，求其他所有线段.

生5：已知OC=6，AB=16，求其他所有线段.

生6：已知OE=5，AC=3，求其他所有线段.

生7：已知DE=10，AB=6，求其他所有线段.

生8：已知OB=10，CD=4，求其他所有线段.

生9：已知BC=4，CD=2，求其他所有线段.

【评析】上述片段是在学了垂径定理，并解决了例题之后所进行的教学环节.通过教师元问题的创设，不仅让学生弄清了本题图中各线段之间的本质联系，而且以课本例2作为题根进行探究，教会了学生思考问题就应该从问题的本源出发，进一步深入挖掘本质通法，并最终回归到问题本源的思维发展程序，大大提升了学生分析问题、提出问题和解决问题的能力.

三、结束语

新课标强调学生学习数学的过程是一个亲身经历、动手实践、主动探究的过程.因此，在课堂教学中，给学生提供探究的时间和空间就显得尤为重要，这也是初中数学慢教育的体现.教师在整条教学思维主线上所创设的元问题，能引导学生进行自主变式探究，在这一过程中，学生发现问题和提出问题的能力得到提升，这是“生本课堂”的核心诉求.需指出的是，本文中所涉及的整条学生发展思维主线，并非一定在同一节课中实现，而是可以在同一类知识点的学习或复习体系中形成.并通过引导和组织学生进行自主变式探究来挖掘问题本质，寻求解题通性、通法.当然，该教学策略还处在不断的尝试和实践阶段，相信在今后的经验不断总结中，能得到进一步完善和提升.

1.李庾南.预设与生成——“初中数学自学·议论·引导教学法35年探索实践”成果报告［J］.未来教育家，2014（6）.

2.姜晓翔.合理创设元问题自主变式探生成［J］.中国数学教育（初中版），2015（12）.

3.姜晓翔.基于“自主变式”引发“生本探究”［J］.中国数学教育（初中版），2016（10）.

4.郦兴江.致力打造“生本课堂”，智慧推进自主学习［J］.中学数学（下），2016（11）.