基于子域叠加模型的表贴式永磁电机电枢反应磁场分析

李 斌， 董 川， 金世鑫

(1. 天津大学电气与自动化工程学院， 天津 300072；2. 国网辽宁省电力有限公司电力科学研究院， 辽宁 沈阳 110006)

基于子域叠加模型的表贴式永磁电机电枢反应磁场分析

李 斌1， 董 川1， 金世鑫2

(1. 天津大学电气与自动化工程学院， 天津 300072；2. 国网辽宁省电力有限公司电力科学研究院， 辽宁 沈阳 110006)

准确计算表贴式永磁电机的磁场分布是进行电机设计和电机优化的关键。本文建立了表贴式永磁电机的子域叠加模型，通过解析法计算了电机的电枢反应磁场的分布，将电机槽子域分为通电槽和非通电槽，求解单槽通电下的泊松方程和拉普拉斯方程得到其电枢反应磁场，再叠加计算出三相电流下的电枢反应磁场。子域叠加模型简化了激励方式，减少了求解变量的数目，降低了求解的难度。以一台12槽表贴式永磁电机为例进行计算，并将解析法结果与有限元分析的结果进行比较，验证了本文提出方法的可行性和正确性。

永磁电机； 电枢反应； 磁场分析； 子域模型； 解析法

1 引言

永磁电机[1]由永磁体替代了转子的励磁绕组，结构简单，体积小，转矩密度高，鲁棒性强。获得永磁电机气隙磁场的分布，是计算转矩特性、涡流损耗、噪声和振动等的关键。在气隙磁场的求解方法中，有限元法[2,3]适用于多种结构复杂的电机，但速度较慢，在电机的优化设计中不便使用；解析法计算量小，速度快，使用价值高，便于对电机进行优化计算。

表贴式永磁电机的解析法主要有镜像法、保角变换法和子域分析法。镜像法[4]将介质的效应通过镜像电流进行等效，适用范围较窄。保角变换法[5]通过许克变换简化边界，从而求得复杂边界下的磁场分布。子域分析法将电机的横截面分割为若干区域，以矢量磁位为求解变量，结合约束条件建立偏微分方程并求得矢量磁位解。Z. J. Liu等提出了单极单槽模型[6]，单极单槽模型设槽为无限深，仅在一个极距周期范围内进行处理，未考虑槽间相互影响以及槽内磁场分布状况；诸自强等人提出了考虑开槽效应的精确子域模型[7]，又依此提出了半开口槽子域模型，对解析计算进行了优化[8,9]；T. Lubin等人利用P函数和E函数使方程的解在表达上更加清晰[10]，并将多种子域交界面进行归类，得到了多种类型电机的方程通解表达式[11]。在求解过程中，上述研究需对整个电机域进行建模，各次谐波系数由所有槽电流密度确定，方程中的常数项变量多。

本文基于子域分析方法，以单层绕组表贴式永磁电机为研究对象，建立了表贴式永磁电机的电枢反应磁场子域叠加模型。子域叠加模型将电机槽子域分为通电槽和非通电槽，通过求解不同激励下的泊松方程和拉普拉斯方程，得到单槽激励下的电枢反应磁场表达式。然后，根据三相电流下各个槽的电流值，利用叠加关系得到总的电枢反应磁场。子域叠加模型简化了激励方式，减少了求解变量的数目，降低了求解的难度。本文将有限元法计算结果与利用子域叠加模型得到的单槽磁场和整体磁场解析解进行了对比，证明了本文方法的可行性和正确性。

2 解析模型

2.1 模型概述

本文以内转子单层绕组表贴式永磁电机为例进行电枢反应磁场解析，其横截面结构如图1所示。

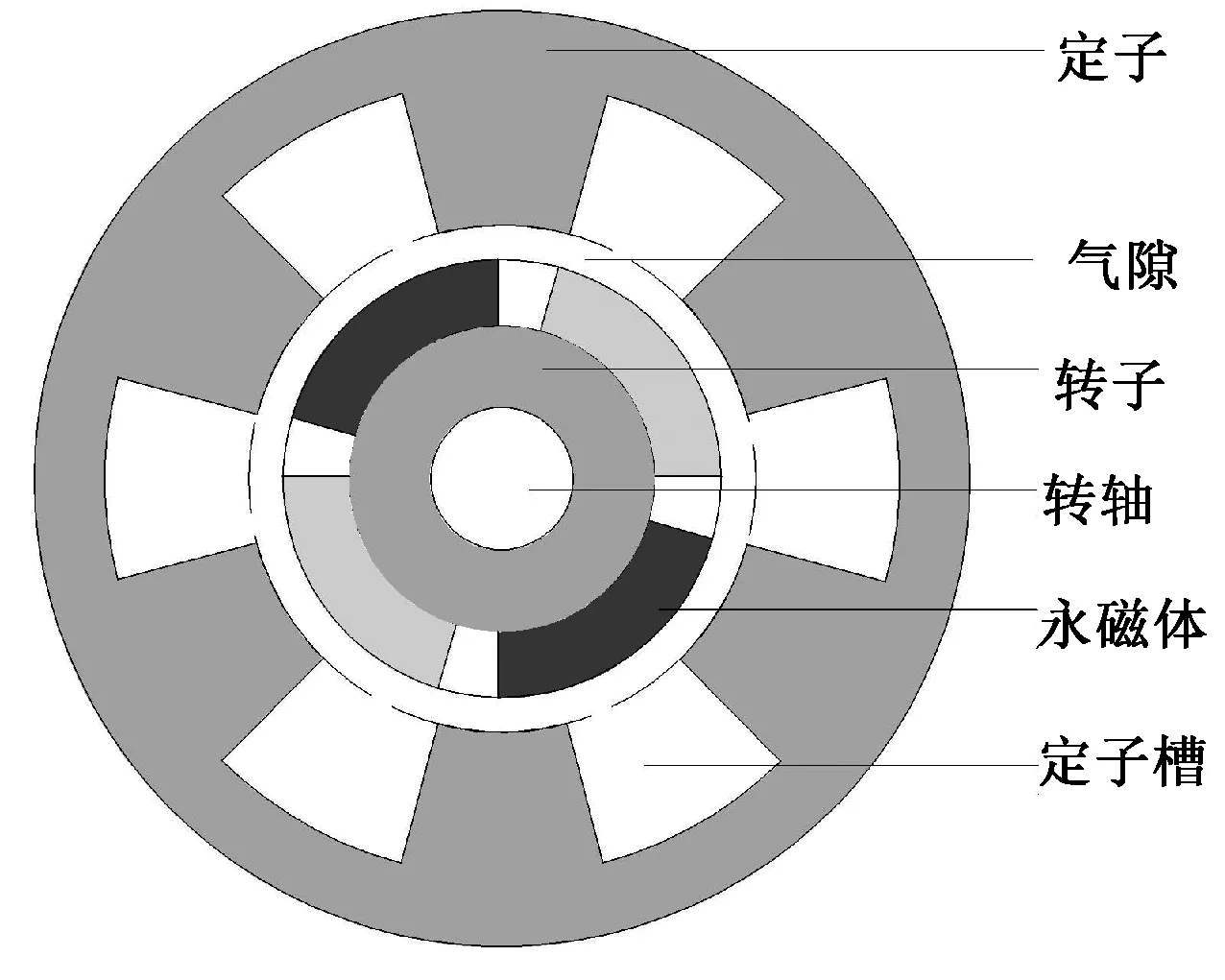
图1 表贴式永磁电机横截面结构示意图Fig.1 Cross section of surface mounted PM machine

电枢反应磁场以定子槽电流为激励，分析所有定子槽以及气隙中的磁场，故将求解区域分解成定子槽子域和气隙子域。该电机的子域示意图如图2所示。R1为转子轭外表面半径，R2为定子内表面半径，R3为定子槽底面半径，显然R3>R2>R1。为突出表示求解的问题，图2中永磁体和转轴略去未画。

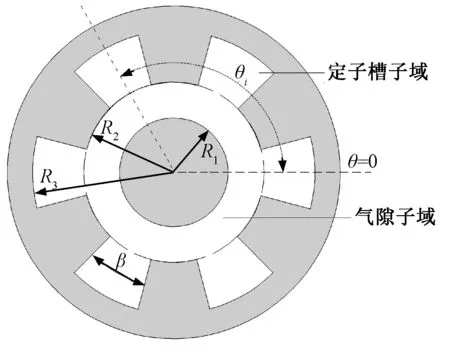
图2 表贴式永磁电机子域示意图Fig.2 Subdomains of surface mounted PM machine

本文对模型中的电机做出如下假设：

(1)定子电流密度仅存在轴向分量，且在槽中均匀分布。

(2)设轴向长度为无穷大，不计端部效应，电机在轴向各处的磁场具有相同的分布形式，因此可将电机的横截面作为分析对象，在极坐标系下进行二维磁场分析。

(3)定子和转子铁心磁导率为无穷大，铁心磁阻产生的影响忽略不计。

电机中定子槽宽角为β；定子槽数为NS；在电机的横截面上建立平面极坐标系，极轴(图中θ=0处)位于一个槽的中心，将该槽编为0号槽，逆时针将其余槽依次编号为1，2，…，NS-1号槽。

编号为i的槽中心所处的角度为：

(1)

本文模型中的表贴式永磁电机可划分为定子槽子域和气隙子域，在定子槽子域中又分为通电槽子域和非通电槽子域，在本文的模型中选定0号槽为通电槽，其余槽为非通电槽。

2.2 通电槽子域通解

通电槽子域中的泊松方程为：

(2)

边界条件为：

(3)

根据分离变量法并代入边界条件可得通电槽子域的通解为：

(4)

式中

(5)

D0m为积分常数；m对应通解中谐波的阶数。

2.3 非通电槽子域通解

本文利用非通电槽的拉普拉斯方程求解，可以省去其电流密度，减少常数项，优化求解过程。

非通电槽即编号为1,2,3,…,NS-1的槽，其子域中的拉普拉斯方程为：

(6)

边界条件为：

(7)

根据分离变量法并代入边界条件可得非通电槽子域的通解为：

(8)

式中，Dim为积分常数；i为对应槽的编号，取1,2,3,…,NS-1。

2.4 气隙子域通解

气隙中的拉普拉斯方程为：

(9)

边界条件为：

(10)

根据分离变量法并代入边界条件可得气隙子域的通解：

(11)

式中，C1n和C2n为积分常数；n为气隙子域解的谐波次数。

2.5 气隙子域径向磁感应强度求解

在平面极坐标系中，气隙子域内磁感应强度的径向分量可表示为：

(12)

2.6 谐波系数求解

气隙子域与通电定子槽子域交界面，有

(13)

由式(4)和式(11)，直流分量部分有如下关系：

(14)

即

(15)

式中

(16)

(17)

各次谐波分量有如下关系：

(18)

即

(19)

式中

(20)

(21)

在气隙子域与非通电定子槽子域交界面，边界条件为：

(22)

结合式(8)和式(11)，直流分量部分关系如下：

(23)

即

(24)

各次谐波分量有如下关系：

(25)

即

(26)

气隙子域与所有定子槽子域交界面均满足如下关系：

(27)

对于所有定子槽均有：

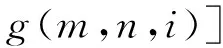
(28)

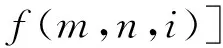
(29)

将所有槽子域和气隙子域中的谐波系数取为有限次，由式(15)、式(19)、式(24)、式(26)、式(28)和式(29)联立可求得各个子域中的所有谐波系数。

3 所有槽通电下解的叠加

本节以气隙径向磁场为例，说明用单槽磁感应强度解计算所有槽通电下的磁感应强度解的过程。

令编号为0的槽中通单位电流，该情况下的气隙径向磁感应强度为：

(30)

式中，I0为0号槽所通的电流值。

编号为i的槽通以单位电流下气隙径向磁感应强度为：

(31)

故在所有槽均通电的情况下，气隙径向磁感应强度为：

(32)

式中，Ii为编号为i的槽的电流值。

4 磁场解析模型的有限元验证

4.1 电机参数

本文选取一台12槽表贴式永磁电机为样机，分析其电枢反应磁场。样机的参数见表1，其绕组分布如图3所示。

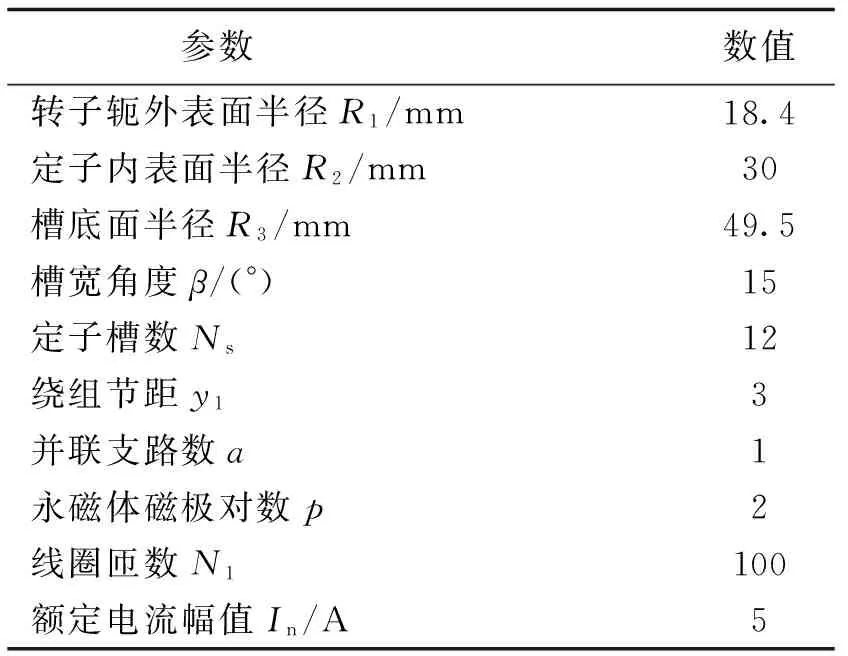
表1 表贴式永磁电机样机参数Tab.1 Parameters of surface mounted PM machine

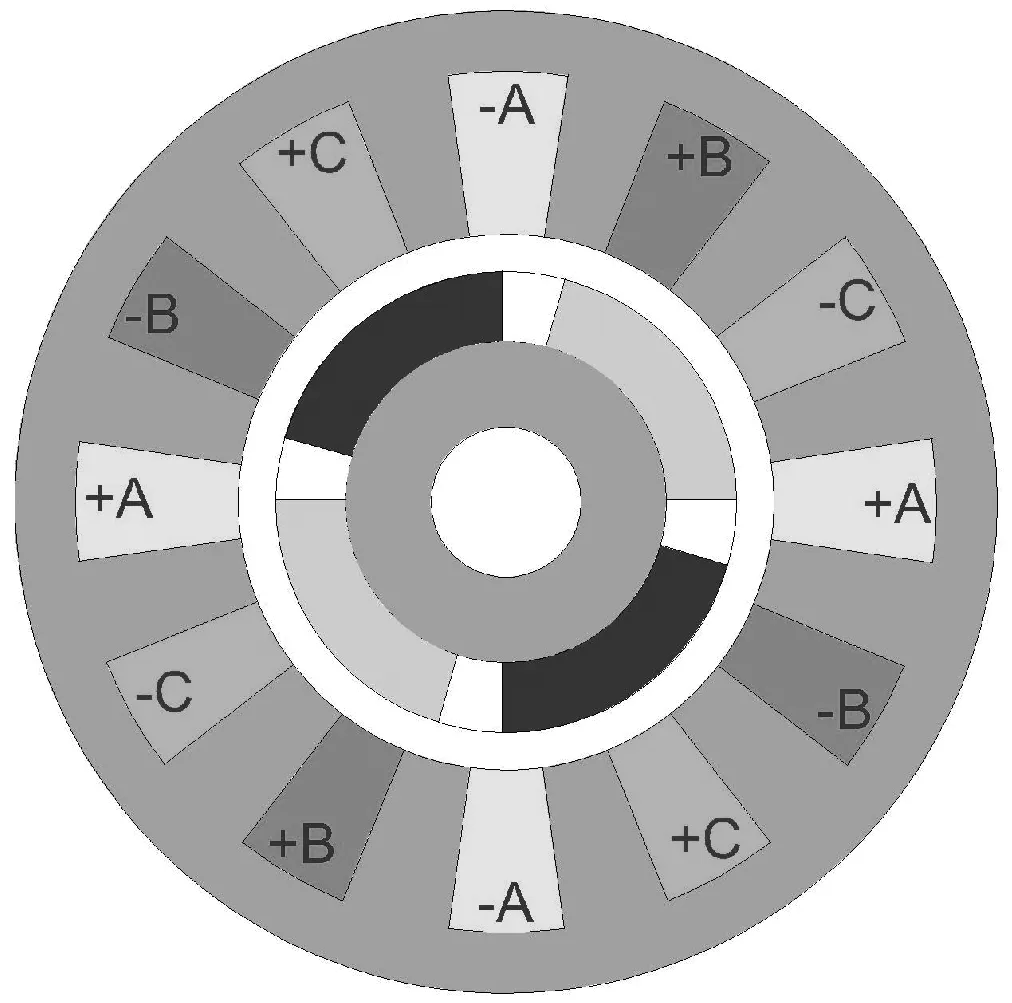
图3 表贴式永磁电机样机绕组分布图Fig.3 Winding distribution of surface mounted PM machine

4.2 气隙磁感应强度分布

样机在单槽通电时(电流大小为5A)电枢反应下的磁感线分布如图4所示。

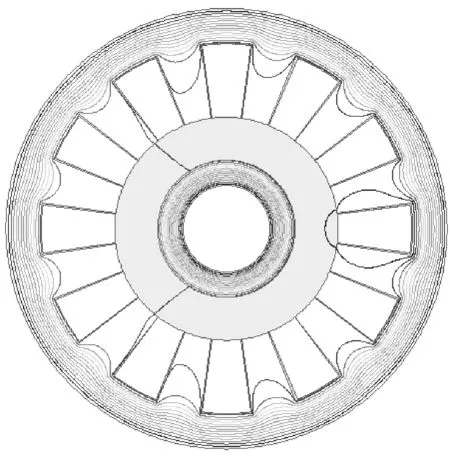
图4 单槽通电电枢反应下磁感线分布Fig.4 Distribution of magnetic induction lines generated by single slot

单槽通电时(电流大小为5A)用解析法求得的气隙内半径为29mm处的电枢反应径向磁感应强度计算结果与有限元法的对比如图5所示。解析法和有限元法计算得到的径向磁感线强度的各次谐波分量比较如图6所示，其中解析法的磁感应强度的基波分量较有限元结果偏离3.13%。

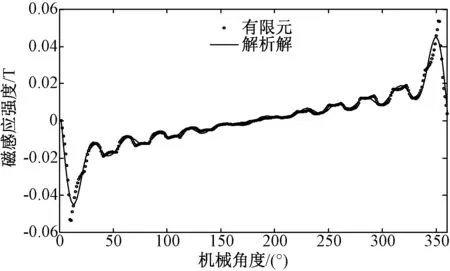
图5 单槽通电下径向磁感应强度Fig.5 Radial components of armature reaction magnetic flux density generated by single slot

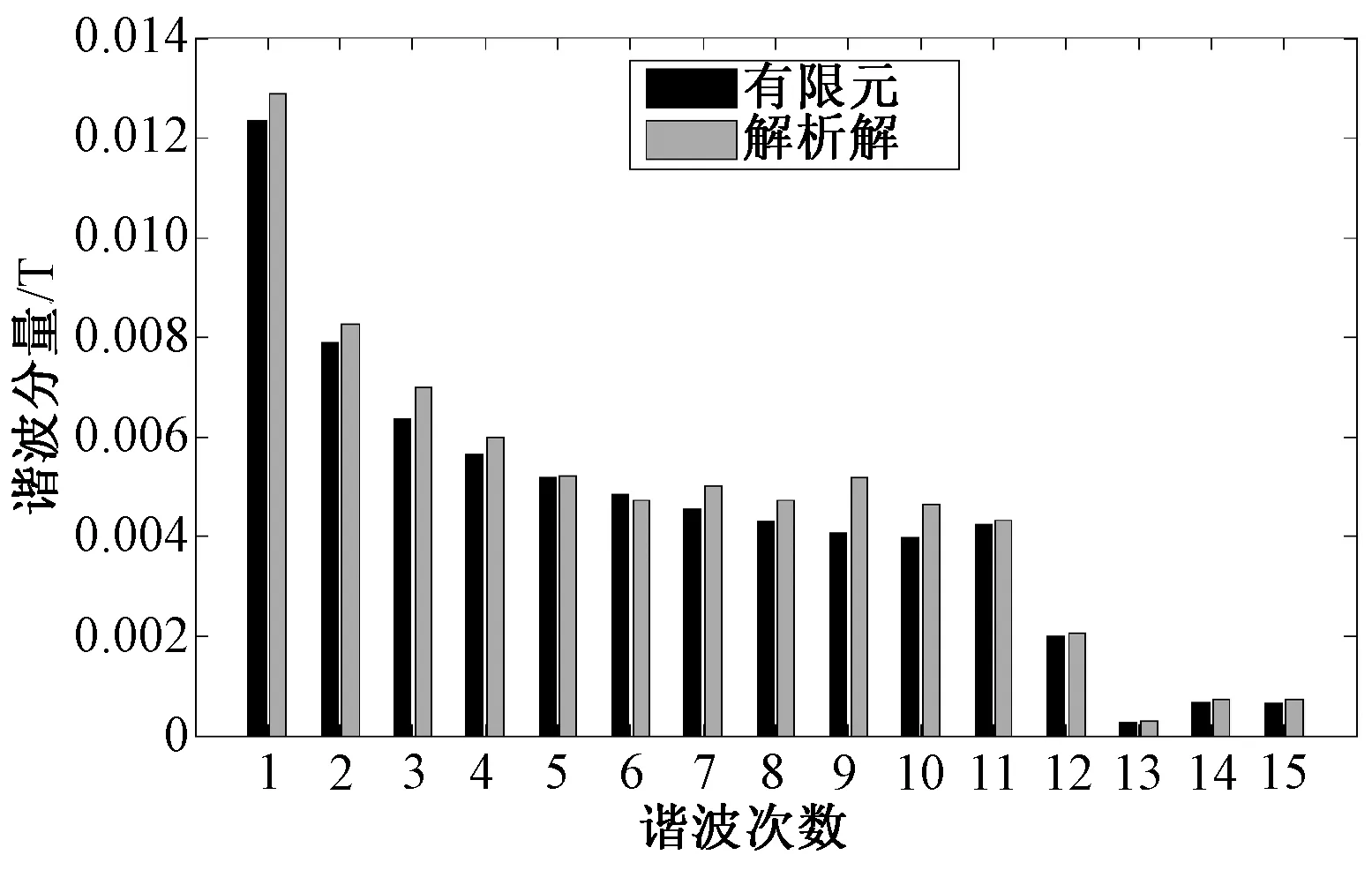
图6 单槽通电下各次谐波分量Fig.6 Harmonic spectra of flux densities in airgap of armature reaction generated by single slot

图7和图8分别为两种不同情况下多槽通电时用解析法求得的气隙内半径为29mm处电枢反应径向磁感应强度计算结果与有限元法所得结果的对比。

其中，图7为三相电流瞬态情况为：Ia=5A，Ib=Ic=-2.5A，在气隙内半径为29mm处的电枢反应下径向磁感应强度计算结果。图8为三相电流瞬态情况为：Ia=0，Ib=-4.33A，Ic=4.33A，在气隙内半径为29mm处的电枢反应下径向磁感应强度计算结果。

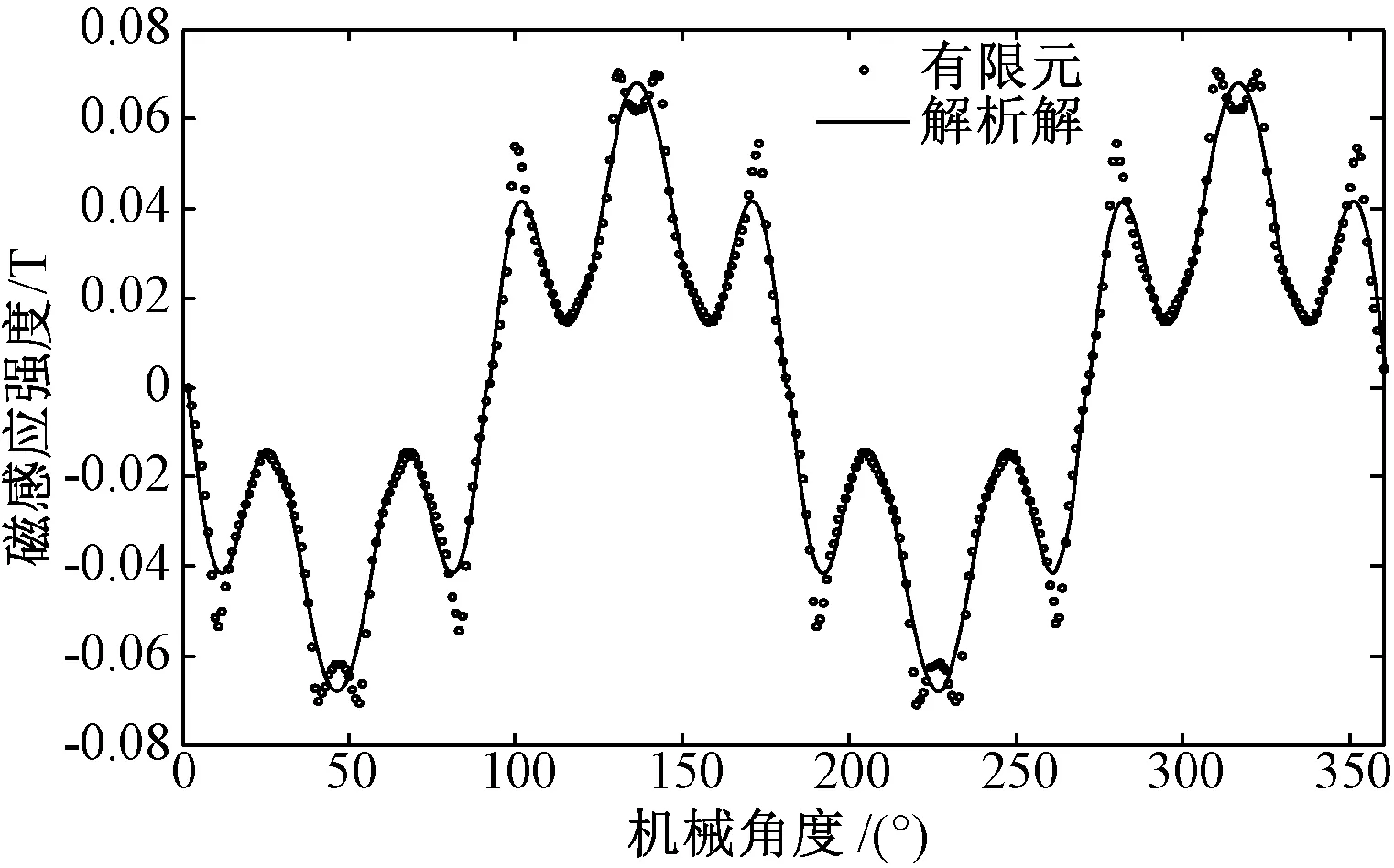
图7 所有槽通电下径向磁感应强度1Fig.7 Radial components of armature reaction magnetic flux density of condition 1

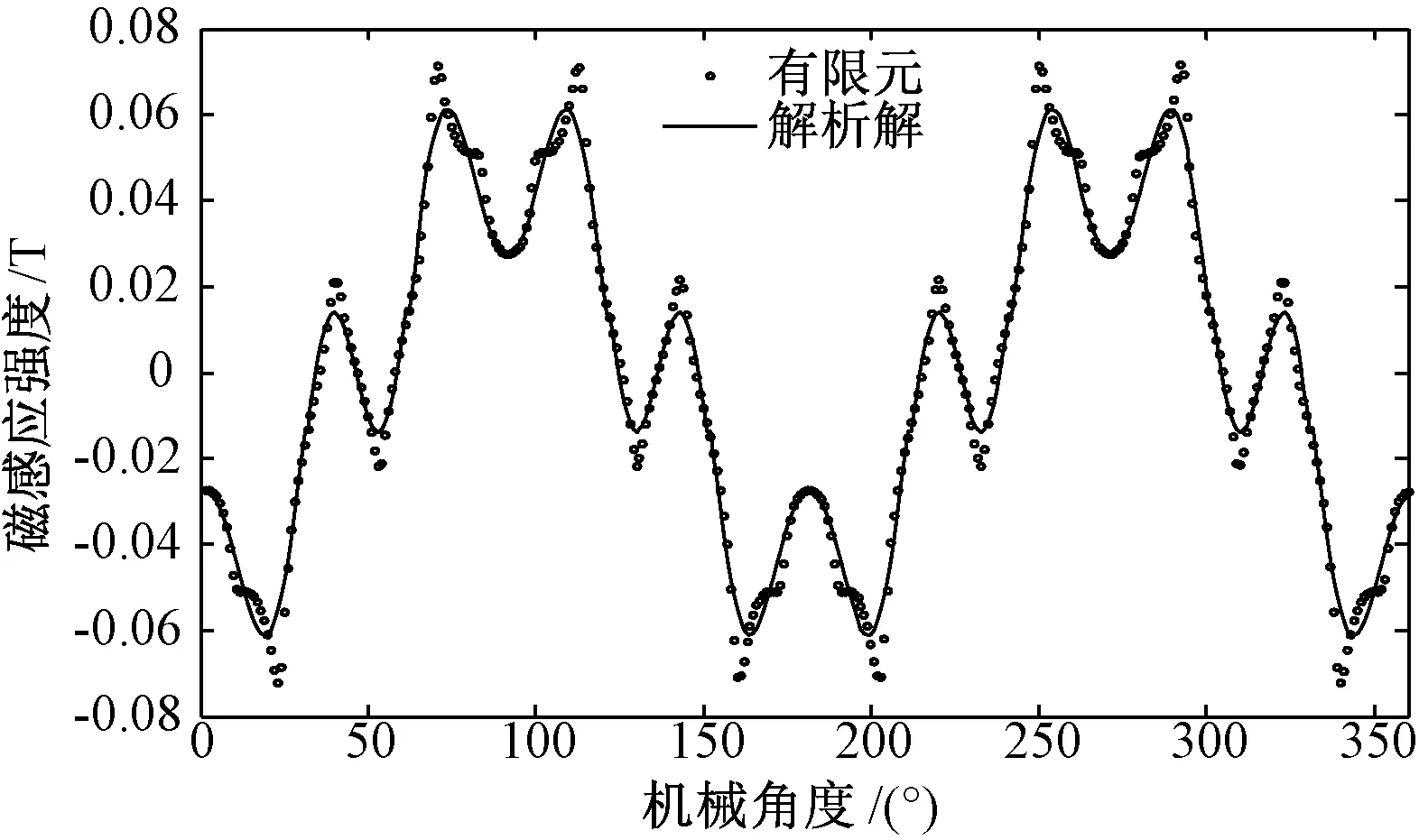
图8 所有槽通电下径向磁感应强度2Fig.8 Radial components of armature reaction magnetic flux density of condition 2

分析图7可得，解析法的磁感应强度基波分量较有限元结果偏离约为3.07%，而图8中偏离约为3.05%，两种方法得到的结果总体上吻合。由于本文仅取气隙区域磁感应强度的前1～15次谐波进行线性方程组求解，因此实际结果中的一些不平滑的点在解析解中体现得不够明显，造成了解析解与有限元解的差异。

5 结论

针对表贴式永磁电机的电枢反应磁场解析方法，本文建立了子域叠加模型，提出了一种比较简便的子域计算方法。本文先计算出较为简单的单槽激励磁场，再通过叠加关系获得较为复杂的总的定子槽磁场和气隙磁场。本文利用二维有限元分析法对气隙磁感应强度进行验证，进一步证明了结果的正确性。本文模型和方法为分析表贴式永磁电机的电磁性能和涡流损耗等奠定了基础。

[1] 刘清，王太勇, 董靖川，等(Liu Qing，Wang Taiyong,Dong Jingchuan, et al.). 基于ESO 的永磁同步电机直接转矩控制(Direct torque control of permanent magnet synchronous motors based on ESO)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2012, 31(1): 35-38.

[2] 阎秀恪, 王振芹, 于向东，等(Yan Xiuke, Wang Zhenqin, Yu Xiangdong, et al.). 基于场路耦合模型的超高压自耦变压器电磁场研究(Research of electromagnetic field for extra-high voltage (EHV) autotransformer based on magnetic field circuit co- upled model)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015,34(11): 43-47.

[3] 梁斯庄，沈建新 (Liang Sizhuang，Shen Jianxin). 永磁同步电机永磁体涡流损耗的二维有限元估算(2D-FEM estimation of eddy current loss in permanent magnets of PMSM)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(1): 52-75.

[4] S H Lee，J S Jeong，K T Jung, et al. Advanced 3-dimensional magnetic field analysis of superconducting machines using analytical method [J]. IEEE Transactions on Applied Superconductivity, 2013, 23(3): 4900704.

[5] D Zarko, D Ban, T A Lipo. Analytical solution for cogging torque in surface permanent-magnet motors using conformal mapping[J]. IEEE Transactions on Magnetics, 2008, 44(1) : 52-65.

[6] Z J Liu, J T Li. Analytical solution of air-gap field in permanent-magnet motors taking into account the effect of pole transition over slots [J]. IEEE Transactions on Magnetics, 2007, 43(10): 3872-3883.

[7] Z Q Zhu, L J Wu, Z P Xia. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines [J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100-1115.

[8] L J Wu, Z Q Zhu, D Staton, et al. Subdomain model for predicting armature reaction field of surface-mounted permanent-magnet machines accounting for tooth-tips [J]. IEEE Transactions on Magnetics, 2011, 47(4): 812-822.

[9] L J Wu, Z Q Zhu, D Staton, et al. An improved subdomain model for predicting magnetic field of surface-mounted permanent magnet machines accounting for tooth-tips [J]. IEEE Transactions on Magnetics, 2011, 47(6): 1693-1704.

[10] Thierry Lubin, Smail Mezani, Abderrezak Rezzoug. 2-D exact analytical model for surface-mounted permanent-magnet motors with semi-closed slots [J]. IEEE Transactions on Magnetics, 2011, 47(2): 479-492.

[11] Kamel Boughrara, Thierry Lubin, Rachid Ibtiouen. General subdomain model for predicting magnetic field in internal and external rotor multiphase flux-switching machines topologies [J]. IEEE Transactions on Magnetics, 2013, 49(10): 5310-5325.

Subdomain superposition model of armature reaction magnetic field of surface mounted permanent-magnent machine

LI Bin1, DONG Chuan1, JIN Shi-xin2

(1. School of Electrical Engineering and Automation, Tianjin University, Tianjin 300072, China;2. Liaoning Electric Power Research Institute, Shenyang 110006, China)

Accurate calculation of the magnetic field of surface mounted PM machine is the key for designing and optimizing the machine. A subdomain superposition model is proposed to calculate the distribution of armature reaction magnetic field of surface mounted PM machine. In the proposed method, only one slot is excited and distinguished from other slots, so the different excitation method is applied to the Maxwell equations. Then the magnetic field generated by single slot can be calculated, and the total magnetic field of all three-phase current excitation is superposed. Subdomain superposition model facilitates the mode of excitation, reducing the amount of the variables and the difficulty of calculating. Taking a 12 slot surface-mounted permanent magnet machine as an example, the results computed by the analytical method are compared with finite-element method, which prove the feasibility of the method.

permanent magnet machine; armature reaction; magnetic field analysis; subdomain model; analytic method

2016-04-06

李 斌(1976-)， 男， 山东籍， 副教授， 博士， 研究方向为新型电机的设计与控制(通讯作者)； 董 川(1991-)， 男， 北京籍， 硕士研究生， 研究方向为电机电磁场分析。

TM351

A

1003-3076(2017)01-0010-06