一种新型双三相无轴承永磁同步电机结构原理及控制研究

袁建飞， 朱熀秋， 赵玉亮， 丁 泉

(江苏大学电气信息工程学院， 江苏 镇江 212013)

一种新型双三相无轴承永磁同步电机结构原理及控制研究

袁建飞， 朱熀秋， 赵玉亮， 丁 泉

(江苏大学电气信息工程学院， 江苏 镇江 212013)

针对传统无轴承永磁同步电机内部两套绕组结构复杂、可靠性低等缺点，提出了一种新型双三相绕组结构的无轴承永磁同步电机。电机采用分布式绕组结构并分为两个空间对称的独立三相绕组单元，通过两个三相逆变器在两个绕组单元中同时通入两组不同序列的电流实现电机的无轴承运行。推导了悬浮力与转矩数学模型。在Ansoft中建立有限元模型，分析了电机在两组电流控制下的磁场分布状况，分别计算了悬浮力与转矩随电流变化的关系，以及偏心磁拉力与转子偏移量的关系，仿真模型计算结果与理论模型计算结果基本吻合。建立了一种控制电机对称相电流不平衡的控制策略，将电机等效为两个普通三相电机，两个电机控制部分中的空间矢量脉宽调制模块SVM所需的信号由转矩电流参考值和悬浮力电流参考值合成再调制得到。采用Matlab软件构建了仿真系统，仿真结果表明，本文提出的双三相无轴承永磁同步电机在该控制策略下能够实现转子的高速旋转与稳定悬浮。

无轴承电机； 双三相绕组结构； 结构原理； 有限元分析； 控制策略

1 引言

随着科学技术的发展，各工业对现代永磁电机的设计与应用要求越来越高，既要满足高转速特性、高功率因数，又要具有无污染、无噪声、寿命长等特点。由于无轴承电机具有转速高、无磨损、无润滑等优势，越来越受到工业界的关注，其在医药制造、半导体制造、高速离心机、电动汽车飞轮储能、航空航天等特殊电气传动领域具有广泛的应用前景[1]。传统的无轴承电机定子侧都是嵌有两套绕组，即转矩绕组和悬浮力绕组，分别注入转矩电流和悬浮力电流产生极对数相差为1的磁场，以提供足够的转矩和稳定的悬浮力[2]。但两套绕组绕制方向和叠绕位置相对严格的限制，增加了电机结构设计和加工工艺的复杂性，且增大了电机定子侧的功率损耗[3]。

针对传统双绕组无轴承电机存在的以上缺点，许多国内外学者对此进行了大量的研究，尝试简化无轴承电机内部结构，降低其功率损耗和成本，提高电机运行的可靠性。其中，文献[4,5]提出了一种无轴承单相薄片电机，采用四个集中式绕组通入两组电流产生悬浮力和转矩，并对其控制方式进行了研究，实现了电机基于功率最优电流控制策略的无轴承运行。该电机虽然简化了内部结构,但启动转矩较低且悬浮力波动较大，只能应用在对启动转矩和悬浮力要求不高的场合。文献[6,7]提出了一种新型绕组结构的无轴承永磁电机，分别分析了该电机利用径向气隙控制轴向磁通产生轴向悬浮力和利用径向气隙控制径向磁通产生径向悬浮力的工作原理。这种结构形式使得电机只能适用于小尺寸小功率场合，对电极设计精度及绕组安排要求很高，尽管结构简单，但加工难度并未降低。文献[8]提出了一种采用中点电流注入法来减小悬浮力脉动的新型无轴承永磁同步电机，该结构使得气隙磁场的一侧磁密强度改变,而保持另一侧磁密强度不变,从而打破气隙平衡磁场达到使转子悬浮的目的。由于这种悬浮方式只改变一侧的磁密强度，造成悬浮力减小了一半，使得电机悬浮性能不高。文献[9]提出了一种采用桥式绕组结构的无轴承永磁电机，能够消除绕组内的感应电压，但电机需要三个隔离功率源的单相逆变器提供悬浮力电流，使得控制较为复杂，成本提高。文献[10,11]利用多相电机谐波丰富的特点提出了一种单绕组五相无轴承电机，基于特定的电机结构控制基波产生1对极磁场，控制2次谐波产生2对极磁场，从而产生稳定的悬浮力。尽管电机采用多相绕组，但并没有实现电机的容错性能，增加了电机设计与控制成本。文献[12,13]提出了一种采用六相系统的单绕组无轴承薄片电机，能够实现无轴承电机的容错功能，并对其功率系统进行研究和设计。文献[14,15]提出一种外转子结构、额定功率为300W的无轴承永磁电机，通过驱动转矩电流与悬浮力电流的叠加控制6个电枢齿上的绕组，永磁体采用8对极使得电磁转矩的输出达到最优。文献[12-15]的两种电机采用集中式绕组结构，相比较分布式绕组结构，电机存在着振动较高、噪声较大的缺点。文献[16]提出一种交替极分段式无轴承电机，其中定子铁心分为独立的4个部分，电磁转矩由4个分离部分合成产生，悬浮力的生成原理类似于传统的电磁轴承。

本文提出一种新型双三相无轴承永磁同步电机分布式绕组拓扑结构，采用隔离中性线的连接方式将电机内的绕组构成两个空间对称的独立三相绕组单元，由两个传统的三相逆变器分别在两个三相绕组单元内同时通入两组不同序列的电流打破电机内的磁场平衡，通过调节两组电流的幅值与相位可以控制转矩和径向悬浮力，从而实现电机的无轴承运行。尽管依然采用了两套绕组，但制作工艺与普通电机类似，电机结构设计的复杂性大大减小，且无需加入双绕组结构所必需的绕组间绝缘材料，使得成本降低，更有利于磁悬浮电机的产业化。同时为简化控制策略，建立了一种控制电机对称相电流不平衡的控制策略，即将电机等效为两个普通三相电机，转矩电流参考值与悬浮力电流参考值经合成后，再调制得到每个三相电机单元所需要的参考电压。

2 双三相无轴承永磁同步电机结构与工作原理

图1(a)为传统的双绕组无轴承永磁电机绕组结构。电机定子侧嵌有两套绕组(转矩绕组和悬浮力绕组)，其中转矩绕组产生与永磁体极对数相同的磁场来获得电磁转矩，悬浮力绕组产生与转矩磁场极对数相差为1的磁场，两者共同作用产生可控悬浮力。由于电机的无轴承运行需要两套绕组共同作用实现，绕组占用更多的空间，不可避免地造成电机内部绕组结构复杂，损耗增大。

图1(b)为本文提出的双三相无轴承永磁同步电机的绕组结构。它通过在一台24槽定子结构的普通永磁同步电机内嵌入两个独立的三相绕组单元，然后在两个三相绕组单元内同时通入两组不同序列的电流共同产生转矩与悬浮力。其中一组电流为转矩电流，用以产生2对极磁场与永磁转子作用生成电磁转矩。另一组电流为悬浮力电流，用以产生1对极磁场以打破气隙内的平衡磁场，从而生成可控径向悬浮力。从结构上看，图1(b)所示的新型双三相无轴承永磁电机可视为双Y移180°的普通双三相永磁同步电机[17,18]。同传统的双绕组无轴承电机一样，所提出的电机同样需要两个三相逆变器为其供电。

图1 传统双绕组与新型双三相无轴承永磁电机Fig.1 Traditional double windings and novel dual three-phase bearingless motor

图2为新型双三相无轴承永磁同步电机结构剖面图。电机转子上的永磁体采用平行充磁4极表贴式结构[19]。6相定子绕组分布在24个定子槽内，每相绕组占4个槽，每三相绕组组成1组独立的绕组单元。其中{A 相，B 相，C相}为第一组三相绕组单元，相与相之间的分布空间上相差120°，{U 相，V 相，W 相}为第二组三相绕组单元，相与相之间的分布空间上也相差120°。每组三相绕组单元中的各相绕组依次排列，分布在定子圆周的一侧，使得两组三相绕组单元空间上相差180°，在定子机械空间中呈镜像分布。即对应相A相与U相、B相与V相、C相与W相在空间上呈对立分布。

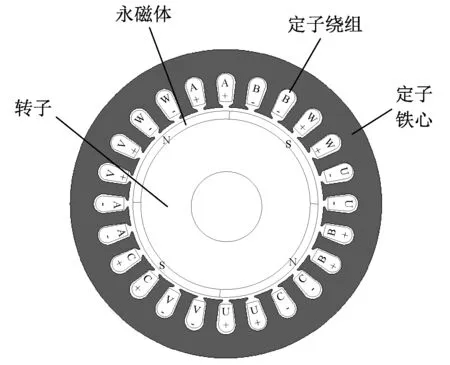
图2 新型双三相无轴承永磁同步电机Fig.2 Novel dual three-phase bearingless permanent magnet motor

图1(b) 电机剖面内⊗表示电流流入平面，⦿表示电流流出平面。因此当给该电机注入转矩电流时，同属于一组三相绕组单元中的各相绕组的电流相位相差120°，两组三相绕组单元中的绕组对应相相位相同。当给该电机注入悬浮力电流时，同属于一组三相绕组单元中的各相绕组的电流相位同样相差120°，但两组三相绕组单元中的绕组对应相相位相差180°。同时为保证两个磁场的旋转方向一致，每相绕组的电流方程应为：

(1)

式中，it(A-W)为每相绕组转矩电流；is(A-W)为每相绕组悬浮力电流；It与Is分别表示两组电流的幅值；ω为绕组转矩和悬浮力电流的电角频率。

（4）壁水蕴德星君，司圖書，驚墊日紏稠梗治。（《太上說玄天大聖真武本傳神呪妙經註》卷一，《中华道藏》30/533）

(2)

3 系统数学模型

3.1 径向悬浮力数学模型

新型双三相无轴承永磁同步电机转子悬浮所需要的径向力可以通过麦克斯韦张量法求得[20]。设电机中气隙磁密为B，真空磁导率为μ0，则作用在转子表面dS面积上的麦克斯韦力为：

(3)

电机的气隙磁密B分为转矩电流与永磁体等效电流产生的气隙磁密Bt和悬浮力电流产生的气隙磁密Bs：

(4)

式中，μ、λ分别为两组电流产生磁场对应磁密的初始相位；θ为气隙圆周的空间角度。则作用在转子表面单位圆并沿X、Y轴方向上的径向悬浮力Fx、Fy分别为：

(5)

式中，l为电机转子铁心有效长度；r为转子半径。

由于6相系统气隙磁动势基波幅值可以由线圈匝数和绕组电流表示，则电机气隙中基波磁动势f(θ)大小为：

(6)

式中，N为绕组每相串联有效匝数；ke为绕组系数；Itr为转矩电流与永磁体合成等效电流幅值；Is为悬浮力电流幅值。

(7)

电机磁通密度与气隙磁动势的关系式为：

(8)

将式(6)～式(8)代入式(5)中进行积分，即

(9)

假定转子偏心位移远小于气隙长度，通过简化式(9)，并将电流矢量转化到dq同步坐标系下，推导得出转子沿X、Y轴方向上的径向悬浮力，并用矩阵表示为[21]：

(10)

式中，isd、isq分别为同步坐标系下绕组悬浮力电流dq轴分量；itd、itq分别为同步坐标系下绕组转矩电流dq轴分量；ird为同步坐标系下永磁转子电流等效d轴分量。

当转子偏心时由于气隙不均匀造成偏心磁拉力，其表达式为：

(11)

式中，k为与电机结构有关的比例系数。

假定转子质量为m，转子的中心在径向悬浮力Fx、Fy、外在干扰力Fzx、Fzy和偏心磁拉力Fsx、Fsy的共同作用下运动，其位移方程为：

(12)

3.2 转矩数学模型

双三相无轴承永磁同步电机转矩系统数学模型与普通永磁同步电机相同。但由于电机可分为两个标准对称的三相电机单元，因此电压方程可等效为两个三相电机来建立，其在dq同步坐标系下的数学模型如下：

(13)

磁链方程为：

(14)

在同步坐标系下的电磁转矩方程为：

(ψr+ψd(UVW))iq(UVW)-id(UVW)ψq(UVW)]

(15)

旋转运动方程为：

(16)

式中，Udq(ABC)、Udq(UVW)分别为同步坐标系下的两个三相绕组单元电压；idq(ABC)、idq(UVW)分别为同步坐标系下的两个三相绕组单元电流；ψdq(ABC)、ψdq(UVW)分别为同步坐标系下的两个三相绕组单元磁链；Rs为电机内阻；ψr为永磁转子产生的磁链；p为微分算子；ωr为转子角速度；Ld、Lq为同步坐标系下的dq轴电感；J为转子转动惯量；Te、TL分别为电机电磁转矩和负载转矩；P为转子极对数。

4 基于Ansoft对电机模型有限元分析

模型仿真参数如表1所示，采用Ansoft Maxwell 12有限元电磁分析软件对提出的双三相无轴承永磁同步电机建立仿真分析模型[22,23]。

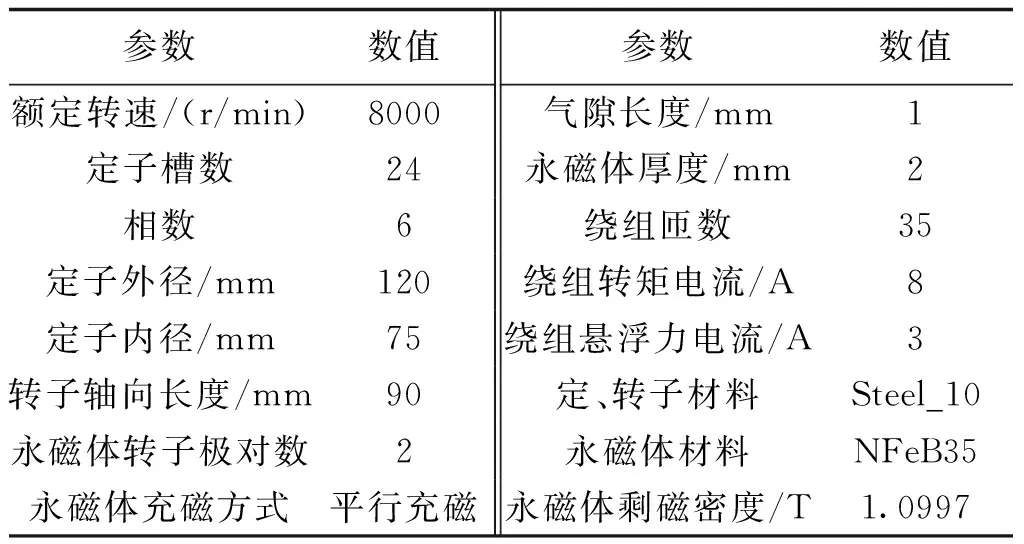
表1 双三相无轴承永磁同步电机模型参数Tab.1 Parameters of dual three-phase bearingless permanent magnet motor

图3(a)为双三相无轴承永磁同步电机分析模型内只通入8A转矩电流，不通入悬浮力电流时的磁力线分布图，此时电机内部磁场呈2对极分布，永磁体充磁后电机只输出电磁转矩。图3(b)为电机分析模型内只通入8A悬浮力电流，不通入转矩电流时的磁力线分布图，此时磁力线呈1对极分布，与图3(a)所示磁场极对数相差1。图3(c)为电机分析模型内同时通入8A转矩电流和3A悬浮力电流时的合成磁力线分布，由于两组电流产生的磁场相互叠加，从而使电机内部气隙磁通密度发生变化，磁力线虽呈2对极分布，但可以看出电机在X轴负方向上的磁通密度较大，而X轴正方向的磁通密度较小，根据麦克斯韦力产生原理，可知电机产生了沿X轴负方向的径向悬浮力。

图3 通入各电流分量时的磁通分布Fig.3 Flux distribution in each current component

由于在传统的双绕组无轴承永磁电机研究领域中，为简化计算，通常将永磁体等效为电机转矩绕组上的等效电流。因此，在分析或计算该双三相无轴承永磁同步电机时，也通常将永磁体等效为绕组通入的转矩电流。图4为有限元分析值和理论计算值。

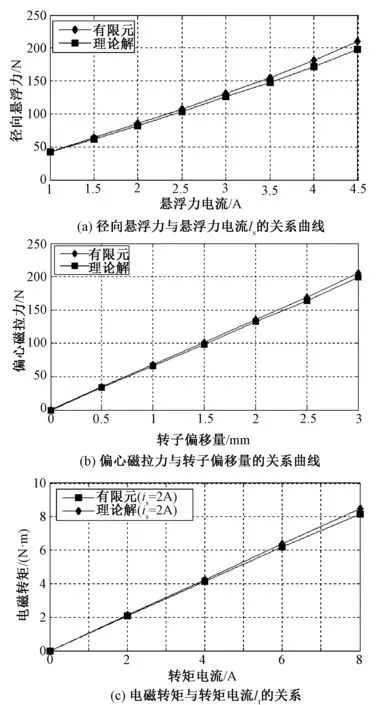
图4 有限元分析值和理论计算值Fig.4 Finite element analysis and theoretical calculation

图4(a)为直接用永磁体进行有限元分析和采用永磁体等效电流进行理论计算的情况下，可控径向悬浮力与悬浮力电流的关系曲线对比。可以看出，有限元分析和理论计算得到的径向悬浮力合力与悬浮力电流的关系曲线基本吻合时，表明数学模型是比较准确的。图4(b)为在不通入电流时直接用永磁体有限元分析和采用永磁体等效电流理论计算的情况下，双三相无轴承电机偏心磁拉力与转子偏移量之间的关系曲线对比，两者都近似地呈线性关系且结果几乎一致。表明转子偏心时，由于气隙的不均匀会产生偏心磁拉力且两者呈正比关系，同时证明了数学模型的正确性。图4(c)为双三相无轴承电机在始终通入2A悬浮力电流时直接用永磁体有限元分析和采用永磁体等效电流理论计算的情况下，得出的电磁转矩与转矩电流大小的关系曲线对比。可知由悬浮力电流幅值和相位可以确定唯一方向的稳定悬浮力，且对电磁转矩不会造成影响。

5 控制系统的设计及仿真

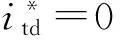
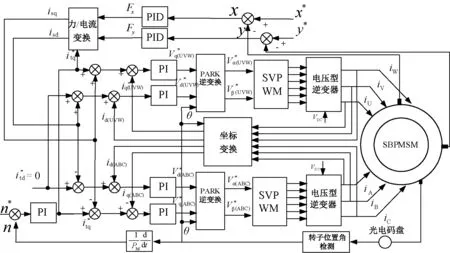
图5 双三相无轴承永磁同步电机控制系统框图Fig.5 Control system of dual three-phase bearingless motor

悬浮力控制部分是将X、Y轴的转子位置指令值分别与实际位移值比较后得到位移差值，经PID调制后生成悬浮力参考值，然后通过力与电流变换模块生成同步坐标系下悬浮力电流参考值，得到的参考值分别与两个三相电机单元中的转矩电流参考值做和值与差值，再与实时反馈的电流值比较后经PI调制得到气隙磁场所需要的电压参考值，采用空间矢量脉宽调制模块SVM调制，实现双三相无轴承永磁电机转矩与悬浮力的同步控制。

根据图5的控制框图在Matlab软件中搭建其仿真模型。仿真采用的双三相无轴承永磁同步电机的参数为：永磁体为2对极，转子质量m=2.625kg，转动惯量J=0.002kg·m2，每相绕组匝数35匝，转子的初始位置x=-0.45mm，y=-0.2mm。仿真结果如图6所示，仿真时间为0.2s。

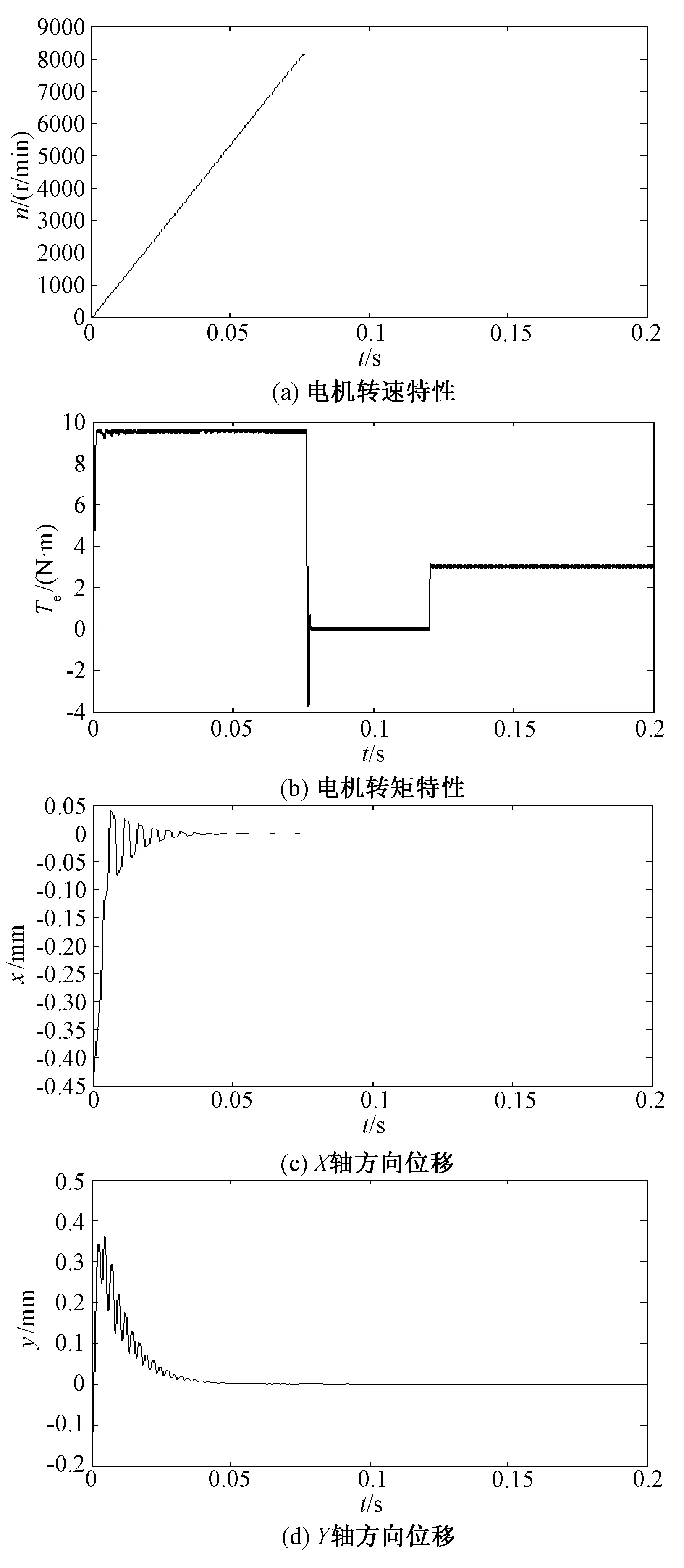
图6 双三相无轴承永磁电机控制系统仿真结果Fig.6 Simulation results of control system of dual three-phase bearingless motor

图6(a)为电机由空载启动加速至给定转速8000r/min的转速响应曲线，调节时间大约为0.075s；图6(b)为转矩动静态响应曲线。电机空载起动，0.075s转速稳定后转矩跳变为零，0.12s时突加3N·m的负载转矩。可以看出，转矩变量能迅速达到设定值，转子系统依然具有良好的动、静态性能。

图6(c)和图6(d)分别为X、Y轴径向位移曲线。转子质心起始位置x、y值设为-0.45mm、-0.2mm， 转子给定位置x、y值都设为0。可以看出，位移调节时间约为0.03s；在0.12s转矩突变时，X、Y轴径向位移曲线也几乎没有受到影响。

图7给出了转子起浮轨迹图。起动时，由于重力作用，转子质心由起始位置快速移动，然后沿着钟摆形运动轨迹逐渐逼近平衡位置，经过0.03s，转子最终处于平衡位置，保证了电机转子的快速稳定悬浮。最终仿真结果表明，新型的双三相无轴承永磁同步电机能够实现转矩的快速响应和转子的稳定悬浮。

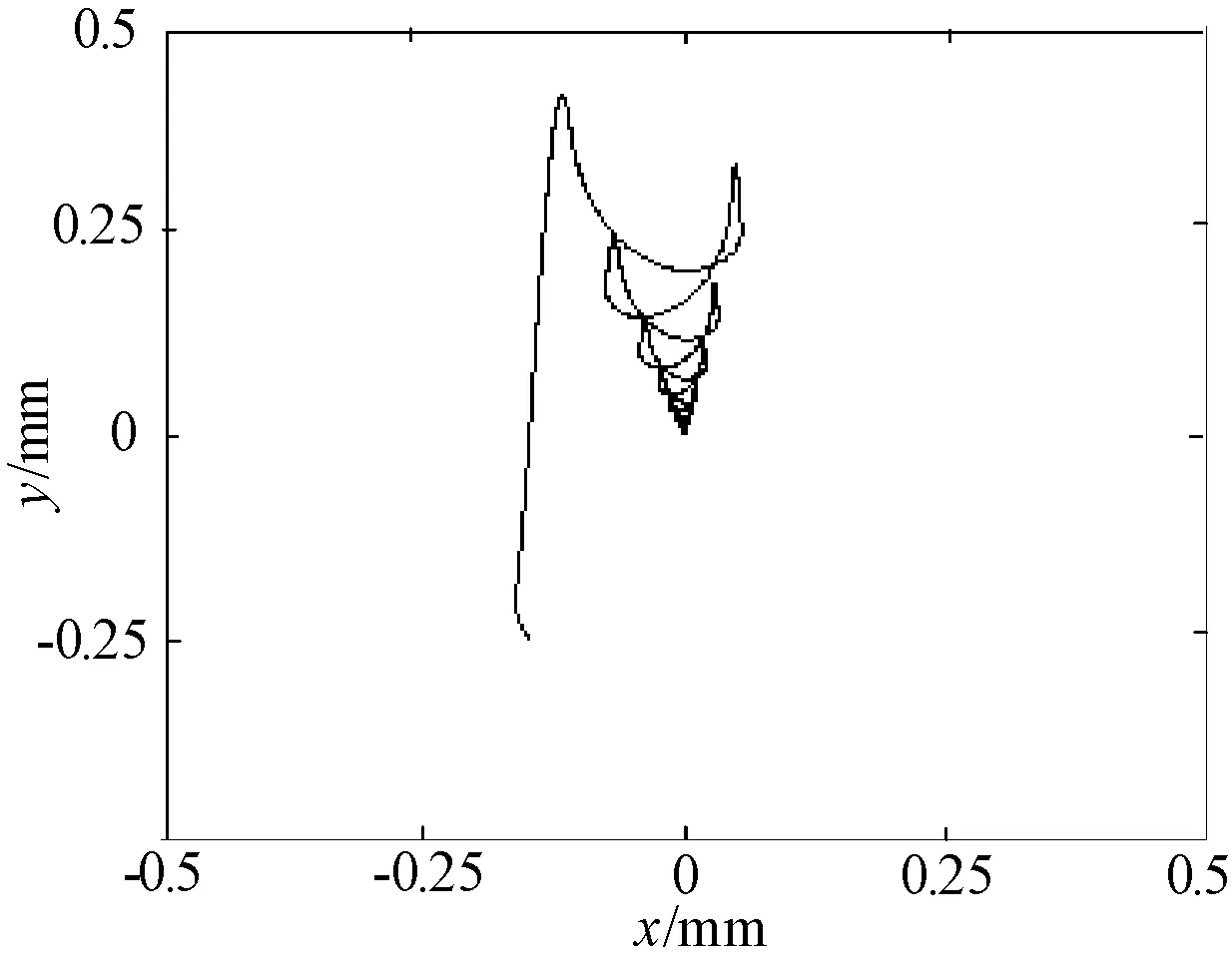
图7 转子起浮轨迹图Fig.7 Rotor trajectory

图8为电机开始运行时，转子在X轴和Y轴正方向始终存在20N干扰力，绕组A相和U相在一段时间内的电流值。当电机空载时，与普通电机一样，各相电流幅值相等，但转子受到某一方向干扰力后，电机绕组A相和U相电流幅值会变得不等，由此说明电机定子内的气隙磁场在整个圆周内是不平衡的，能够产生确定的径向悬浮力。

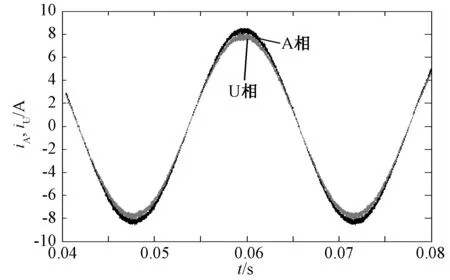
图8 A相与U相绕组电流Fig.8 Phase A and phase U winding current

6 结论

新型双三相无轴承永磁同步电机采用分布式绕组结构，分为两个空间对称的独立三相绕组单元，通过两台三相逆变器在两个绕组单元中通入两组电流，实现两套绕组控制电机电磁转矩和径向悬浮力。它不仅具有传统双绕组无轴承电机的优点，也使得电机内部结构更加简单，定子侧功率损耗变小。

本文利用有限元软件分析了新型电机产生的径向悬浮力、偏心磁拉力与电磁转矩，仿真结果与数学模型理论计算结果基本一致，验证了数学模型的正确性。同时建立了一种控制电机对称相电流不平衡的控制策略，即将电机等效为两个普通三相电机，转矩电流参考值与悬浮力电流参考值经合成后再调制得到每个三相电机单元所需要的参考电压，从而控制两个三相电机共同提供转矩与悬浮力。由于电机转矩部分可以等效为速度与电流的双闭环控制，悬浮力部分可以等效为位移与电流的双闭环控制，因此转子系统的动、静态响应较为快速。利用Matlab软件对双三相无轴承永磁同步电机的磁场定向控制进行了仿真，其结果表明该电机能够实现稳定的悬浮和获得良好的调速性能。

[1] 成秋良, 朱熀秋, 王成波(Cheng Qiuliang, Zhu Huangqiu, Wang Chengbo). 无轴承永磁同步电机研究现状与发展趋势 (Research status and development trend of bearingless permanent magnet synchronous motors)[J]. 微电机(Micro-motor)，2010，43(3)：76-80.

[2] Hui Li, Huangqiu Zhu. Bearingless motor’s radial suspension force control based on virtual winding current analysis[A]. IEEE 17th International Conference on Electrical Machines and Systems (ICEMS) [C]. 2014. 2141-2146.

[3] W K S Khoo. Bridge configured winding for polyphase self-bearing machines[J]. IEEE Transactions on Magnetics, 2005, 41(4): 1289-1295.

[4] K Nenninger, W Amrhein, S Silber. Bearingless single-phase motor with fractional pitch windings[A]. The 7th International Symposium on Magnetic Bearings[C]. 2000. 371-376.

[5] S Silber, W Amrhein. Power optimal current control scheme for bearingless PM motors[A]. The 7th International Symposium on Magnetic Bearings[C]. 2000.401-406.

[6] H Sugimoto, S Tanaka, A Chiba. Winding arrangement in single-drive bearingless motor with radial gap[A]. IEEE International Power Electronics Conference[C]. 2014. 982-987.

[7] J Asama, Y Hamasaki, T Oiwa. Proposal and analysis of a novel single-drive bearingless motor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(1): 129-138.

[8] A Chiba, K Sotome, Y Iiyama. A novel middle point current injection type bearingless PM synchronous motor for vibration suppression[J]. IEEE Transactions on Industrial Application, 2011, 47(4): 1700-1706.

[9] W K S Khoo, K Kalita, S D Garvey. Practical implementation of the bridge configured winding for producing controllable transverse forces in electrical machines[J]. IEEE Transactions on Magnetics, 2011, 47(6): 1712 -1718.

[10] 黄进, 康敏, 杨家强(Huang Jin, Kang Min, Yang Jiaqiang). 新型单绕组多相无轴承电机(Novel bearingless machine with a single set of multiphase windings)[J]. 浙江大学学报(工学版)(Journal of Zhejiang University (Engineering Science)), 2007, 41(11): 1850-1856.

[11] Min Kang, Jin Huang, Haibo Jiang, et al. Principle and simulation of a 5-phase bearingless permanent magnet-type synchronous motor[A]. The 11th IEEE International Conference on Electrical Machines and Systems[C]. 2008. 1148-1152.

[12] 朱俊, 邓智泉, 王晓琳, 等(Zhu Jun, Deng Zhiquan, Wang Xiaolin, et al.). 单绕组无轴承永磁薄片电机的原理和实现(Principle and implementation of the single winding bearingless permanent magnetic slice motor)[J]. 中国电机工程学报(Proceedings of the CSEE), 2008, 28(33): 68-74.

[13] 朱俊, 邓智泉, 王晓琳(Zhu Jun, Deng Zhiquan, Wang Xiaolin, et al.). 单绕组无轴承薄片电机功率系统的设计(Design and realization of single winding bearingless slice motor power system)[J]. 电机与控制学报(Electric Machines and Control), 2008, 12(1): 5-9.

[14] T Reichert, T Nussbaumer, W Johann. Bearingless 300W PMSM for bioreactor mixing[J]. IEEE Transactions on Industrial Electronics, 2012, 59(3): 1376-1388.

[15] T Reichert, T Nussbaumer, W Gruber, et al. Design of a novel bearingless permanent magnet motor for bioreactor applications[A]. IEEE 35th Annual Conference on Industrial Electronics (IECON) [C]. 2009. 1086-1091.

[16] Stallinger T, Gruber W, Amrhein W. Bearingless segment motor with a consequent pole rotor[A]. IEEE Electric Machines and Drives Conference (IEMDC) [C]. 2009. 1374-1380.

[17] 白左霞(Bai Zuoxia)．双三相永磁同步电机容错性能分析(Analysis of fault tolerance performance of the dual three-phase permanent magnet synchronous motor)[D]. 郑州: 郑州大学(Zhengzhou：Zhengzhou University), 2014.

[18] E F Rodriguez, J A Santisteban. An improved control system for a split winding bearingless induction motor[J]. IEEE Transactions on Industrial Electronics, 2011, 58(8): 3401-3408.

[19] 李发宇, 朱熀秋, 祝苏明, 等(Li Fayu, Zhu Huangqiu, Zhu Suming, et al.). 无轴承永磁薄片电机不同转子结构的对比研究(Comparison study on bearingless permanent magnet slice motor with different rotor structures)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(8): 7-12.

[20] Yikang He, Heng Nian. Analytical model and feedback control of the levitation force for an induction-type bearingless motor[A]. The Fifth IEEE International Conference on Power Electronics and Drive Systems[C]. 2003. 242-246．

[21] 卜文绍, 万山明, 黄声华(Bu Wenshao, Wan Shanming, Huang Shenghua, et al.). 无轴承电机的通用可控磁悬浮力解析模型(General analytical model about controllable magnetic suspension force of bearingless motor)[J]. 中国电机工程学报 (Proceedings of the CSEE), 2009, 29(30): 84-89.

[22] 朱熀秋, 张涛(Zhu Huangqiu, Zhang Tao). 无轴承永磁同步电机有限元分析(Finite element analysis for bearingless permanent magnet-type synchronous motors)[J]. 中国电机工程学报(Proceedings of the CSEE), 2006, 26(3): 136-140.

[23] 刘泽远, 杨艳(Liu Zeyuan, Yang Yan). 计及磁场耦合特性的无轴承开关磁阻电机的电磁设计(Electromagnetic design of bearingless switched reluctance motors considering coupled characteristics of magnetic field)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015, 34(10): 44-50.

[24] 王成波, 朱熀秋, 吉裕晖(Wang Chengbo, Zhu Huangqiu, Ji Yuhui). 基于SVPWM的无轴承永磁同步电机转子磁场定向控制系统研究(Study on rotor field oriented control system of bearingless PMSM based on SVPWM)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2010, 29(2): 48-52.

Structure principle and control of novel dual three-phase bearingless permanent magnet synchronous motor

YUAN Jian-fei, ZHU Huang-qiu, ZHAO Yu-liang, DING Quan

(School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013, China)

In view of the disadvantages of complex structure and low reliability of double winding bearingless motor, a novel bearingless permanent magnet synchronous machine with dual three-phase windings topology is proposed. The structure of this motor with distributed winding is divided into two independent and symmetrical three-phase winding units. Currents of two different sequences are fed at the same time into two winding units by using two three-phase inverters to achieve the operation of bearingless motor. And mathematical models of the torque and radial suspension force are deduced. The gap magnetic flux distribution of motor are studied under two groups of current control using finite element method. The finite element analysis results of radial suspension force, torque and eccentricity magnetic force are compared with theoretical calculation results. In addition, a control strategy of supplying unbalanced phase current for controlling the motor is proposed. The motor coils are equivalent to two ordinary three phase motor, and the signals of SVM are synthesized by the reference values of the torque current and the suspension force current. The simulation model based on Matlab is constructed, and the results showed that the motor can achieve stable suspension and get good drive performance.

bearingless motor; dual three-phase windings topology; structure principle; FEA; control strategy

2016-03-23

国家自然科学基金项目(51675244)、 江苏省重点研发计划项目(BE2016150)、 江苏省“333工程”资助项目(2014年)、 江苏省“青蓝工程”资助项目(2014年)

袁建飞(1990-)， 男， 山东籍， 硕士研究生， 主要从事单绕组无轴承永磁电机的设计及控制等研究； 朱熀秋(1964-)， 男， 江苏籍， 教授， 博导， 主要从事无轴承电机设计及控制， 磁悬浮高速传动系统理论及应用等研究。

TM351

A

1003-3076(2017)01-0016-09