考虑光伏逆变器剩余容量的配电网无功优化

吴 杰， 赵凡凡， 赵丽霞

(河北省电力电子节能与传动控制重点实验室, 燕山大学， 河北 秦皇岛 066004)

考虑光伏逆变器剩余容量的配电网无功优化

吴 杰， 赵凡凡， 赵丽霞

(河北省电力电子节能与传动控制重点实验室, 燕山大学， 河北 秦皇岛 066004)

在保证光伏电源有功出力最大的情况下，将光伏逆变器的剩余容量作为连续可调的无功电源研究了含光伏电源的配电网无功优化问题。在分析光伏发电出力随机性和不确定性的基础上，建立了光伏电源出力的概率分布模型，并以配电网有功网损和总电压偏差之和最小为目标函数，建立了考虑光伏逆变器剩余容量的配电网无功优化模型，采用线性递减权重粒子群算法(LinWPSO)对离散变量进行处理，并寻求无功优化最优解。通过IEEE33节点系统算例仿真，验证了本文所提出的模型和方法更接近实际，可以有效降低配电网总电压偏差，改善配电网电压水平，降低配电网有功网损，验证了本文模型和方法的正确性和有效性。

配电网； 光伏电源； 光伏逆变器剩余容量； 线性递减权重粒子群算法； 无功优化

1 引言

近年来，分布式光伏发电得到了广泛地应用[1]。光伏电源接入配电网可以降低配电网的总容量，调节配电网的峰谷性能，降低发电成本。随着光伏渗透率的提高，光伏并网对配电网电压和有功网损的影响越来越大，给配电网的规划调度带来影响[2，3]。研究含光伏电源的配电网无功优化问题可以改善配电网电压质量，降低配电网有功网损，使配电网能够更加经济稳定的运行，具有重要意义。

传统的配电网无功优化主要通过调节有载调压变压器分接头档位和无功补偿装置实现。文献[4]指出通过逆变器控制的分布式电源在输出有功功率的同时，也可以输出一定的无功功率，可以作为连续可调的无功电源参与到配电网的无功优化中。文献[5]和文献[6]分别提出了一种具有无功补偿功能的单级式和两级式三相光伏并网系统，实现了光伏发电系统并网发电和无功补偿相结合的控制方案，在向电网提供有功功率的同时，还能够提供电网所需的无功功率，为光伏逆变器参与配电网无功优化提供了技术支持。

如今已有文献对含分布式电源配电网进行无功优化的研究。文献[7]将分布式电源无功出力与传统的电压调节手段相结合，建立了无功优化的多智能体免疫模型，利用多智能体免疫算法实现无功优化；文献[8]以配电网有功网损最小为目标函数建立无功优化数学模型，但模型中没有考虑分布式电源的无功出力；文献[9]建立了以配电网有功网损最小为目标函数，电压越限作为惩罚项的无功优化数学模型，优化对象为小型水电站；文献[10]针对间歇性风电使得基于实时无功优化的电压控制效果劣化问题，基于电压越限概率建立了无功优化控制模型；文献[11]建立了以系统有功网损与节点电压偏差之和最小为目标函数的含风电场配电网的无功优化模型，采用粒子群优化算法进行求解。

上述文献均在分布式电源有功和无功出力恒定的前提下进行无功优化的研究，未考虑分布式电源出力的随机性和不确定性，因此优化结果较片面。本文在分析了光伏发电有功和无功出力随机性和不确定性的基础上，建立光伏发电输出功率的概率分布模型，以配电网有功网损和总电压偏差之和最小为目标函数，在保证光伏电源有功出力最大的情况下，以光伏逆变器的剩余容量、有载调压变压器分接头档位和无功补偿电容器组出力为控制变量，建立无功优化数学模型，采用线性递减权重粒子群算法对控制变量中的离散变量进行处理，以IEEE33节点系统为算例进行仿真，取得了良好结果。

2 含光伏电源的配电网无功优化模型

2.1 光伏逆变器剩余容量的无功调节能力分析

目前广泛使用的光伏逆变器的功率因数一般在-0.98(滞后)～0.98(超前)之间连续可调，因此光伏逆变器具有一定的剩余容量，可以合理利用这部分剩余容量对配电网进行无功补偿，参与配电网无功优化。光伏并网逆变器拓扑结构如图1所示。

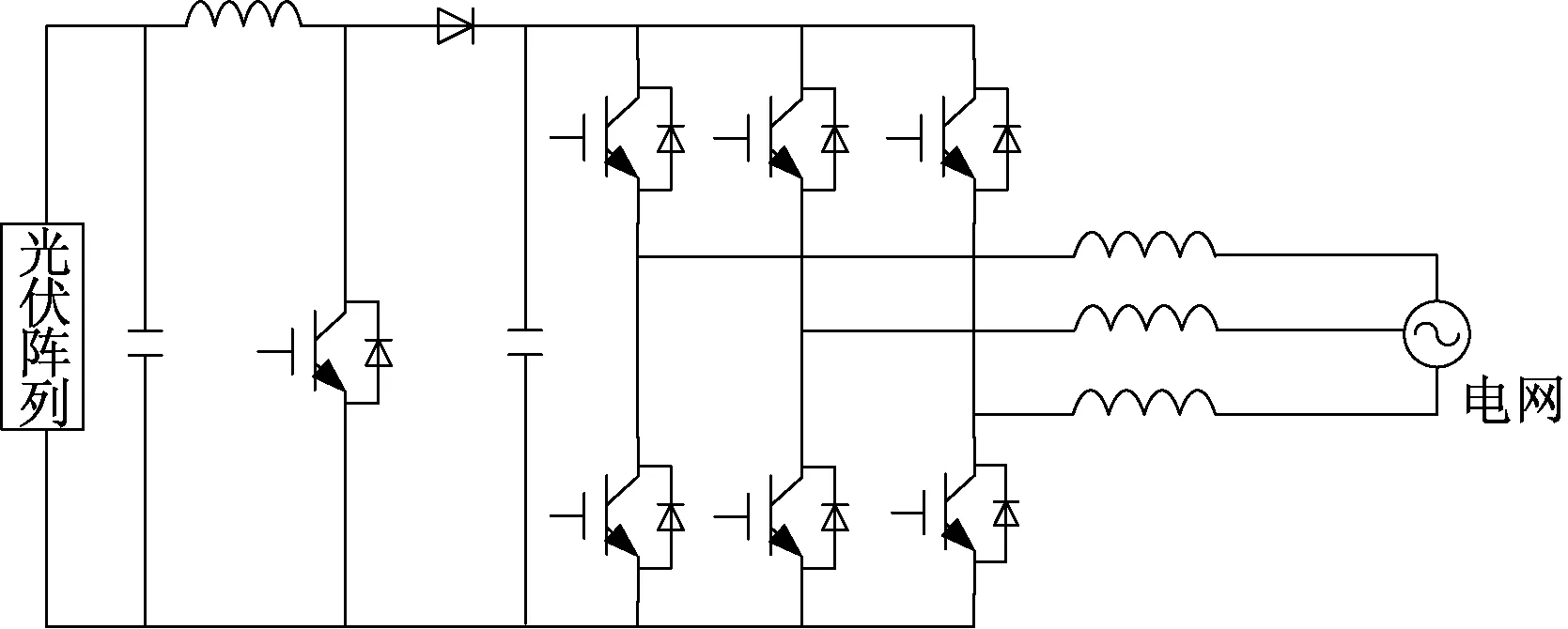
图1 光伏并网逆变器示意图Fig.1 Schematic diagram of photovoltaic grid connected inverter

光伏逆变器的剩余容量由光伏逆变器的运行容量和光伏电源输出的有功功率决定，如式(1)所示。

(1)

式中，S为光伏逆变器的运行容量；PPV为光伏电源输出的有功功率；|QPV|max为光伏逆变器的剩余容量，表征光伏逆变器的最大无功调节能力。

光伏电源输出的有功功率主要取决于日照强度和温度等条件。当日照强度或者温度过低使光伏电源输出功率低于设定的最低值而停止输出有功功率时，光伏逆变器仍可以向电网提供无功功率。因此，可以将传统无功优化方法与光伏逆变器剩余容量的无功调节能力相结合，对配电网进行无功优化，不仅可以节省无功补偿设备投资，还可以改善配电网电压质量，降低系统网损。

2.2 光伏发电系统出力的概率分布模型

光伏发电输出的有功功率受日照强度和温度等自然条件的影响，具有一定的随机性和不确定性。典型晴好天气下光伏发电功率输出曲线如图2所示。

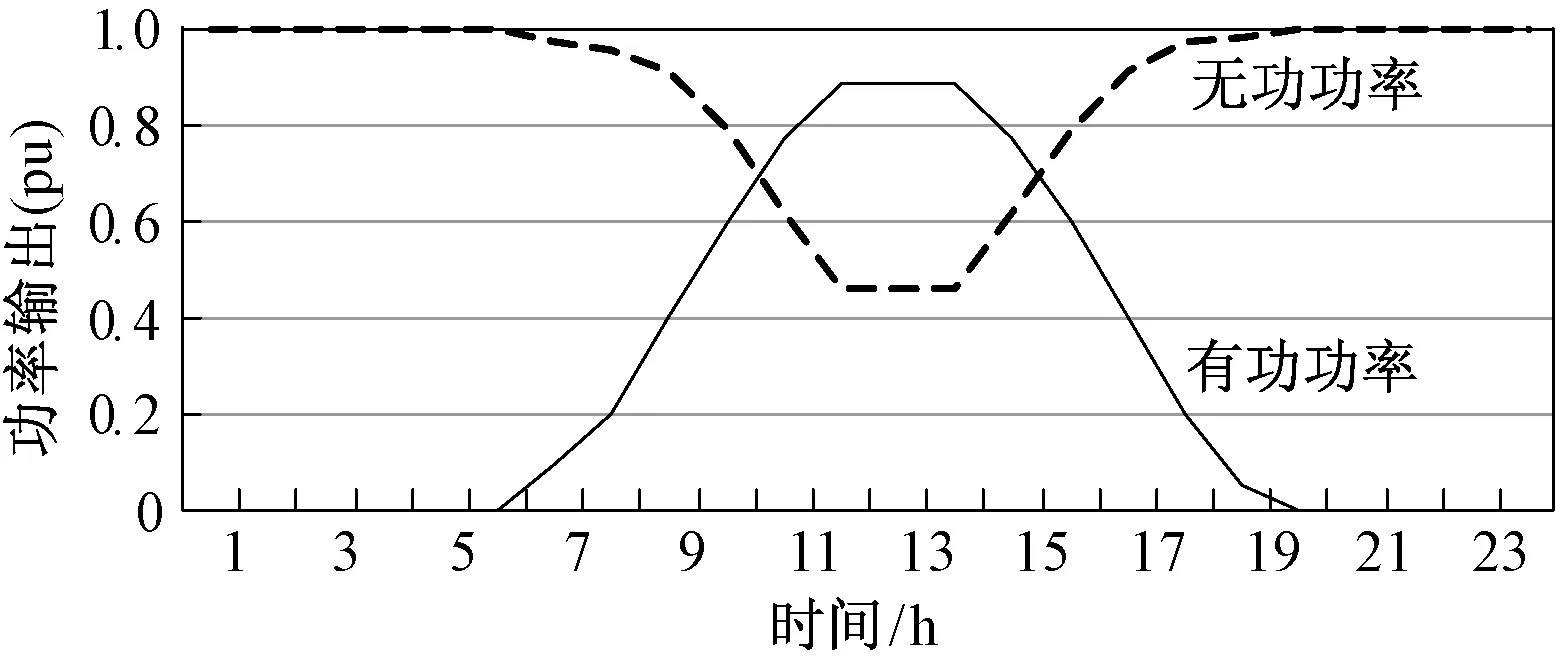
图2 光伏发电系统功率输出曲线Fig.2 Power output curve of PV power generation system

考虑光伏发电出力的随机性和不确定性，建立光伏发电输出功率的概率分布模型。建模思路为：

(1)将图2所示的晴好天气下光伏发电系统输出功率的连续变化曲线分为24时段，将动态功率输出转化为各时段上的静态功率输出，结果见表1。

(2)采用小时晴空指数时间序列的方法[12]对光伏发电输出功率进行间歇性处理。小时晴空指数取 0.54，计算得出每个时段光伏发电输出功率的概率分布。

选取1MW光伏电源为例，根据上述方法，得到光伏发电系统每个状态出力的概率分布，见表1。

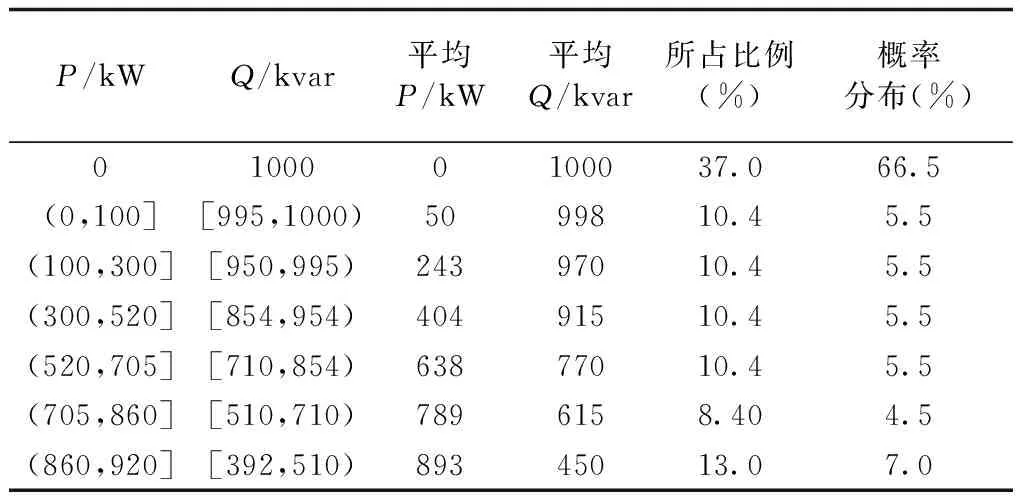
表1 光伏发电系统出力的概率分布Tab.1 Probability distribution of output of photovoltaic power generation system

2.3 含光伏电源的配电网无功优化模型

本文建立了将光伏电源剩余容量、补偿电容器组无功出力和有载调压变压器分接头档位协调控制的无功优化模型，考虑分布式光伏发电出力的随机性和不确定性，在满足配电网安全运行的约束条件下使配电网有功网损和各节点总电压偏差之和最小。

2.3.1 目标函数

考虑系统运行的安全性和经济性，以配电网有功网损和总电压偏差之和最小为目标函数，电压越限情况以惩罚项的形式表示，目标函数如式(2)所示。

(2)

式中

x为控制变量，x=[Qpv，Ttk，LC];Qpv为光伏逆变器剩余容量的无功出力向量;Ttk为有载调压变压器分接头档位向量，Ttk=[Ttk1，Ttk2，…，TtkNt];Nt有载调压变压器台数;LC为无功补偿电容器组投切组数向量，LC=[LC1，LC2，…，LCNC];NC为无功补偿电容器组投切组数；PLoss为系统有功网损；M 为光伏电源出力状态数；PiLoss为在第i种出力状态时，配电网无功优化前后有功损耗；a为第i种出力状态的概率分布(见表1最后一列)；Ui为除平衡节点以外配电网各节点的电压；Uspec为各节点电压期望值；Uimax、Uimin分别为节点电压的上下限取值；λ1、λ2分别为有功网损最小和电压偏差最小的权重系数；λ为节点电压越限惩罚系数；n为除平衡节点外系统的节点数。

2.3.2 约束条件

(1)等式约束条件

等式约束条件即为潮流方程：

(3)

式中，PGi、QGi分别为电网向节点i注入的有功功率和无功功率；PPVi为光伏电源向节点i注入的有功功率;QPVi为光伏逆变器向节点i注入的无功功率；PLi、QLi分别为节点i处负荷的有功功率和无功功率；QCi为节点i所接无功补偿电容器组的无功出力值；Gij、Bij和θij分别为节点i、j 之间的电导、电纳和电压相角差。

第i台光伏逆变器运行约束

(4)

式中，SPVi为第i台光伏逆变器的运行容量；PPVi为光伏电源输出的有功功率；QPVi为光伏逆变器的剩余容量。

(2)不等式约束条件

不等式约束条件分为控制变量约束条件和状态变量约束条件。本文以光伏逆变器剩余容量、有载调压变压器分接头档位和无功补偿电容器组出力作为控制变量，将配电网各节点电压幅值作为状态变量。

控制变量约束条件为：

(5)

(6)

(7)

式中，QPVi.min、QPVi.max为第i个光伏逆变器输出无功功率的最大值和最小值；Ttk.min、Ttk.max分别为第k台有载调压变压器的分接头位置的上下限值；QCj.min、QCj.max为第j组无功补偿电容器输出无功功率的最大值和最小值。

状态变量约束条件为

(8)

式中，Ui.min、Ui.max分别为第i个节点的电压上下限值。

3 基于线性递减权重粒子群算法的考虑光伏逆变器剩余容量的配电网无功优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)是近年来发展起来的一种新型进化算法。这种算法以其实现容易、精度高和收敛快等优点[13]引起了学术界的重视，并且在电力系统无功优化方面得到了广泛地应用。其中，线性递减权重粒子群算法(LinWPSO)在基本PSO的基础上，采用线性变化的权重，克服了基本粒子群算法容易早熟以及算法后期易在全局最优解附近产生振荡现象，因此本文采用线性递减权重粒子群算法对考虑光伏逆变器剩余容量的配电网进行无功优化。在保证光伏电源有功输出最大的同时，充分发挥光伏逆变器剩余容量的无功调节能力，参与配电网的无功优化。控制变量包括光伏逆变器剩余容量、有载调压变压器分接头档位和无功补偿电容器投运组数，其中，光伏逆变器剩余容量为连续变量，有载调压变压器分接头档位和无功补偿电容器组投切组数为离散变量，因此在计算粒子的函数适应度之前要将其离散化。本文方法是采用LinWPSO算法对粒子位置进行近似取整，算法的其余部分则按照连续粒子群算法求解。虽然这种方法可能会使不同的连续解对应同一个整数解，但文献[14]指出在解决优化问题时，这种算法稳定性较高，可以取得良好结果。

考虑光伏逆变器剩余容量的配电网无功优化步骤如下：

(1)输入配电网相关参数、负荷参数和节点电压上下限值，每个光伏电源的最大有功输出值，每台光伏逆变器的运行容量等。

(2)不考虑光伏逆变器剩余容量的无功调节能力，将光伏电源作为PQ节点参与配电网的潮流计算，得到各节点总电压偏差值及网损值。

(3)保证光伏电源有功输出最大，根据式(1)计算光伏逆变器无功输出的上下限值。

(4)初始化线性递减权重粒子群算法参数，包括种群规模N，惯性权重的最大值ωmax和最小值ωmin，学习因子c1和c2，最大速度Vmax，迭代次数T等，将光伏逆变器剩余容量无功出力、有载调压变压器分接头档位和无功补偿电容器组投运组数作为控制变量进行编码。

(5)随机初始化种群速度和位置，调用潮流计算程序，计算各个粒子的适应度值，找出各个粒子个体最优值pibest和全局最优值gibest。

(6)更新每个粒子的速度和位置，更新惯性权重，再次调用潮流计算程序，重新计算每个粒子的适应度值，如果粒子i的适应值优于此前的个体极值则将其值设为pibest，如果最优pibest优于此前的全局极值gibest，则将其值设为gibest。

(7)判断是否达到最大迭代次数，若满足条件，则停止搜索，否则返回步骤(5)。

本文线性递减权重粒子群算法相应的程序执行流程图如图3所示。

图3 线性递减权重粒子群算法流程图Fig.3 Flow chart of LinWPSO

4 算例分析

为验证本文模型和算法的正确性和有效性，以IEEE33节点配电网系统为算例，在此系统中增加一台有载调压变压器，两个光伏电源和两组无功补偿电容器组，系统拓扑结构如图4所示，系统线路参数参考文献[15]。以节点0为平衡节点，其余节点为PQ节点，基准电压10kV，基准容量10MV·A。有载调压变压器的变比范围为0.95～1.05，分为9档，步进量为1.25%；在节点1和节点12分别接入一个光伏电源，每个光伏电源出力概率分布见表1；在节点17和节点32分别接入一组无功补偿电容器组，两组补偿电容器组的容量分别为150kVar×4和150kVar×7，电压越限惩罚系数λ=3000，本文设定有功网损和总电压偏差两个目标函数的优先级相同，因此λ1=λ2=1。

图4 IEEE33节点系统结构图Fig.4 IEEE33 node system structure diagram

粒子群算法参数设置：种群规模N=40，学习因子c1=c2=2.0，维数D=5，惯性权重ω=0.8，ωmax=0.9，ωmin=0.4，最大迭代次数T为60，最大速度Vmax=2，最小速度Vmin=-2。

为验证本文模型和算法的正确性，对以下三种情况进行对比：①初始潮流；②不考虑光伏逆变器剩余容量，仅以有载调压变压器分接头档位和无功补偿电容器组出力为优化变量，对配电网进行无功优化；③考虑光伏逆变器剩余容量，对配电网进行无功优化。无功优化结果对比见表2，各节点电压幅值情况如图5所示。

从上述优化结果可以看出：

(1)优化前，系统有功网损为237kW，损耗较大，且总电压偏差为1.3695pu，各节点电压波动较大，有多个节点电压越限。

表2 优化结果对比Tab.2 Comparison of optimization results

注：C1和C2分别为节点17和节点32投入的无功补偿电容器组数。

图5 节点电压对比图Fig.5 Node voltage contrast diagram

(2)光伏发电系统具有较强的无功输出能力，充分利用光伏逆变器的剩余容量，参与配电网无功优化，能显著减少配电网的有功损耗，算例中配电网有功损耗从不利用光伏电源无功出力时的237kW降低到利用光伏电源无功出力时的87kW；各节点电压值均在0.95pu以上，较之于传统无功优化，各节点电压更接近期望值，节点电压波动减小，有效发挥了光伏电源对配电网的无功及电压的支撑作用。

(3)考虑光伏逆变器的剩余容量后，无功补偿电容器组投切组数减少，能显著减少配电网无功补偿设备投资，增强配电网运行的经济性。

5 结论

本文在分析光伏发电系统出力随机性和不确定性的基础上，建立光伏发电出力概率分布模型，并以配电网有功网损和总电压偏差之和最小为目标函数建立无功优化模型，运用线性递减权重粒子群算法对算例进行优化求解。算例结果表明，光伏电源具有较强的无功输出能力，考虑并网光伏电源出力随机性和不确定性的出力模型使配电网无功优化结果更接近实际；本文所提出的无功优化模型及方法可以协调控制光伏逆变器剩余容量、有载调压变压器变比和无功补偿电容器组出力，有效发挥光伏电源的无功及电压支撑作用，有效降低系统总电压偏差和系统网损，提高配电网电压合格率，减少无功补偿设备投资，保证配电网系统安全经济运行。

[1] 艾欣，韩晓男，孙英云(Ai Xin，Han Xiaonan，Sun Yingyun).光伏发电并网及其相关技术发展现状与展望(The development status and prospect of grid-connected photovoltaic generation and its related technologies)[J].现代电力(Modern Electric Power)，2013，30(1):1-7.

[2] 丁明，王伟胜，王秀丽，等(Ding Ming，Wang Weisheng，Wang Xiuli，et al.).大规模光伏发电对电力系统影响综述(A review on the effect of large-scale PV generation on power systems)[J].中国电机工程学报(Proceedings of the CSEE)，2014，34(1)：1-14.

[3] 沈鑫，曹敏(Shen Xin，Cao Min).分布式电源并网对于配电网的影响研究(Research on the influence of distributed power grid for distribution network)[J].电工技术学报(Transactions of China Electrotechnical Society)，2015，30(S1)：36-351.

[4]M Braun. Reactive power supply by distributed generators[A]. IEEE Power and Energy Society General Meeting: Conversion and Delivery of Electrical Energy in the 21st Century[C].Pittsburgh, PA, USA，2008.1-8．

[5] 吴理博，赵争鸣，刘建政(Wu Libo，Zhao Zhengming，Liu Jianzheng).具有无功补偿功能的单级式三相光伏并网系统(Implementation of a single-stage three-phase grid-connected photovoltaic system with reactive power compensation)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2006，21(1)：28-32.

[6] 张浙波，刘建政，梅红明(Zhang Zhebo，Liu Jianzheng，Mei Hongming).两级式三相光伏并网发电系统无功补偿特性(Study of reactive power compensation characteristics on a three-phase double-stage grid-connected photovoltaic power system)[J]. 电工技术学报(Transactions of China Electrotechnical Society)，2011，26(S1)：242-246.

[7] 张丽，徐玉琴，王增平，等(Zhang Li，Xu Yuqin，Wang Zengping，et al.).包含分布式电源的配电网无功优化(Reactive power optimization for distribution system with distributed generators)[J].电工技术学报(Transactions of China Electrotechnical Society)，2011，26(3)：168-174

[8] 吕忠，周强，蔡雨昌(Lv Zhong，Zhou Qiang，Cai Yuchang). 含分布式电源的DEIWO算法配电网无功优化(Reactive power optimization in distribution network with distributed generation on DEIWO algorithm)[J].电力系统保护与控制(Power System Protection and Control)，2015，43(4)：69-73.

[9] 王卫平，王主丁，张 昀，等(Wang Weiping，Wang Zhuding，Zhang Yun，et al.).含分布式电源的配网无功优化混合算法(Hybird algorithm for reactive power optimization in distribution networks with distributed generations)[J]. 电力系统及其自动化学报(Proceeding of the CSU-EPSA)，2013,25(6)：93-100.

[10] 原蔚鹏，王孟邻，张勇军，等(Yuan Weipeng，Wang Menglin, Zhang Yongjun，et al.).电压越限概率指标及其在含风电场电网无功优化控制的应用(Reactive power optimization for distribution system with distributed generators)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2016，35(2):62-68,80.

[11] 赵晶晶，符杨，李东东(Zhao Jingjing，Fu Yang，Li Dongdong). 考虑双馈电机风电场无功调节能力的配电网无功优化(Reactive power optimization in distribution network considering reactive power regulation capability of DFIG wind farm)[J].电力系统自动化(Automation of Electric Power Systems)，2011，35(11)：33-38.

[12] 王一波，许洪华(Wang Yibo，Xu Honghua).基于机会约束规划的并网光伏电站极限容量研究(Research of capacity limit of grid-connected photovoltaic power station on the basis of chance-constrained programming)[J].中国电机工程学报(Proceedings of the CSEE)，2010，30(22): 22-28.

[13] 张燕，许伟伟(Zhang Yan，Xu Weiwei). 基于粒子群-差异进化混合算法的电力系统无功优化(Reactive power optimization based on improved particle swarm optimization algorithm)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2014，33(9):48-51,67.

[14] 郭文忠，陈国龙，陈振(Guo Wenzhong，Chen Guolong，Chen Zhen).离散粒子群优化算法研究综述(Survey on discrete particle swarm optimization algorithm)[J].福州大学学报(自然科学版)(Journal of Fuzhou University(Natural Science Edition))，2011，39(5):631-638.

[15] M E Baran， F F Wu. Network reconfiguration in distribution systems for loss reduction and load balancing [J]. IEEE Transactions on Power Delivery, 1989, 4(2): 1401-1407.

Reactive power optimization in distribution network considering residual capacity of photovoltaic inverter

WU Jie， ZHAO Fan-fan， ZHAO Li-xia

(Key Lab of Power Electronics for Energy Conservation and Motor Drive of Hebei Province,Yanshan University, Qinhuangdao 066004, China)

To ensure the maximum active power output of photovoltaic power，the reactive power optimization problem in distribution power system with photovoltaic power is discussed considering the residual capacity of photovoltaic inverter as continuously adjustable reactive power. Based on the analysis of the randomness and uncertainty of PV generation, the probability distribution model of PV power output is established. The objective function is to minimize the sum of active power loss and total voltage deviation in the distribution network, and a reactive power optimization model of distribution network with photovoltaic power is established. The linear decreasing weight particle swarm optimization algorithm (LinWPSO) is adopted to deal with the discrete variables and the reactive power optimization optimal solution is found. The example of IEEE33 node system shows that the model and method proposed in this paper are more close to the real condition, and can effectively reduce the total voltage deviation of distribution network. The distribution network voltage level is improved, and the active power loss of the distribution network is reduced. The correctness and validity of the model and method are verified.

distribution network; photovoltaic power; residual capacity of photovoltaic inverter; linear decreasing weight particle swarm optimization(LinWPSO); reactive power optimization

2016-04-07

吴 杰 (1959-)， 男， 山东籍， 教授， 研究方向为电能质量分析与控制； 赵凡凡 (1992-)， 女， 河北籍， 硕士研究生， 研究方向为含光伏电源配电网的无功优化运行。

TM715

A

1003-3076(2017)01-0038-06