双馈风电场联络线单相接地故障单端测距分析

徐晓宾， 李凤婷， 袁 冰， 刘锦英， 刘宗杰， 周伟绩

(1. 新疆大学电气工程学院， 新疆 乌鲁木齐 830047；2. 国网山东省电力公司济宁供电公司， 山东 济宁 272023)

双馈风电场联络线单相接地故障单端测距分析

徐晓宾1， 李凤婷1， 袁 冰2， 刘锦英2， 刘宗杰2， 周伟绩1

(1. 新疆大学电气工程学院， 新疆 乌鲁木齐 830047；2. 国网山东省电力公司济宁供电公司， 山东 济宁 272023)

针对单相接地故障，风电场联络线故障特性受风电场运行方式、低电压穿越策略等因素影响较大，传统故障测距方法已不能很好地适用于风电场联络线故障测距。为此，本文基于传统单相接地短路解复数方程故障测距方法，研究了双馈风电场序阻抗特性，建模分析了双馈风电场联络线短路电流、电压特性。基于零序网络，指出了该方法在风电场联络线故障测距中产生误差的关键因素，并仿真研究了风电场不同风速和投运机组数对这种因素产生的影响，最后经过迭代补偿故障支路零序电流相位有效提高了测距精度。

双馈风电场； 单相接地； 零序网络； 故障测距

1 引言

随着风电技术越来越成熟，风电场联络线的输送容量和电压等级也不断提高，其担负输送电能的任务更加重要。而风电场高压联络线单相接地故障发生概率最大，若能及时准确定位线路故障，意义重大。目前众多国内外学者针对高压输电线路基于单端单相接地故障测距方面已做了大量工作[1-8]。单端法故障测距是通过利用一端的电气量信息或是检测一端的暂态行波量来实现故障定位，方法简单，经济性好[1-3]。然而单端电气量的采集受过渡电阻、系统对端阻抗、线路分布电容等因素影响较大[4]。行波法虽不受故障阻抗、系统运行方式等因素影响，但突变波头的识别一直是研究的难点[5]。文献[6]基于一端负序电流，拟合故障支路负序电流相位信息，并在故障点电压瞬时过零点时得到测量阻抗，避免了过渡电阻的影响，在常规输电线路中该方法能够精确测距。文献[7,8]则结合阻抗法与行波法测距的各自优点，提出基于两种方法的综合单端测距方法，同样达到了精确的测距效果。文献[9]基于文献[6]测距原理，立足于含风电并网的双端输电系统零序网络，分别从风电场侧与系统侧补偿零序电流相位，减小了对故障点电压相位的拟合误差，使得所提出的改进单端故障测距算法有效提高了测距精度。以上研究内容大都是以常规电源为背景，针对高压输电线路故障测距出现的各种问题提出解决方法，实现故障点精确定位，少有考虑风电接入的影响。然而不同于常规电源，针对单相接地故障，风电场联络线故障特性因风电场运行方式、低电压穿越策略等因素的变化而变化，对于含风电并网的双端输电系统，传统故障测距方法在风电场联络线故障测距中的适用性问题有待分析与解决。

本文首先阐述了基于传统单相接地短路解复数方程故障测距方法的基本原理，并通过所搭建的含双馈风电场并网的双端系统，分别从阻抗、短路电流、电压三方面分析了双馈风电场联络线单相接地故障特性；分析研究了传统解复数方程法在风电场联络线中的故障测距适用性问题。针对风电场联络线单相接地故障存在的测距误差，通过迭代补偿故障支路零序电流相位提高了测距精度。

2 传统单相接地短路解复数方程故障测距方法

图1为输电线路单相系统故障示意图。基于单端电气量的单相接地短路解复数方程测距算法[1]的基本原理如下。

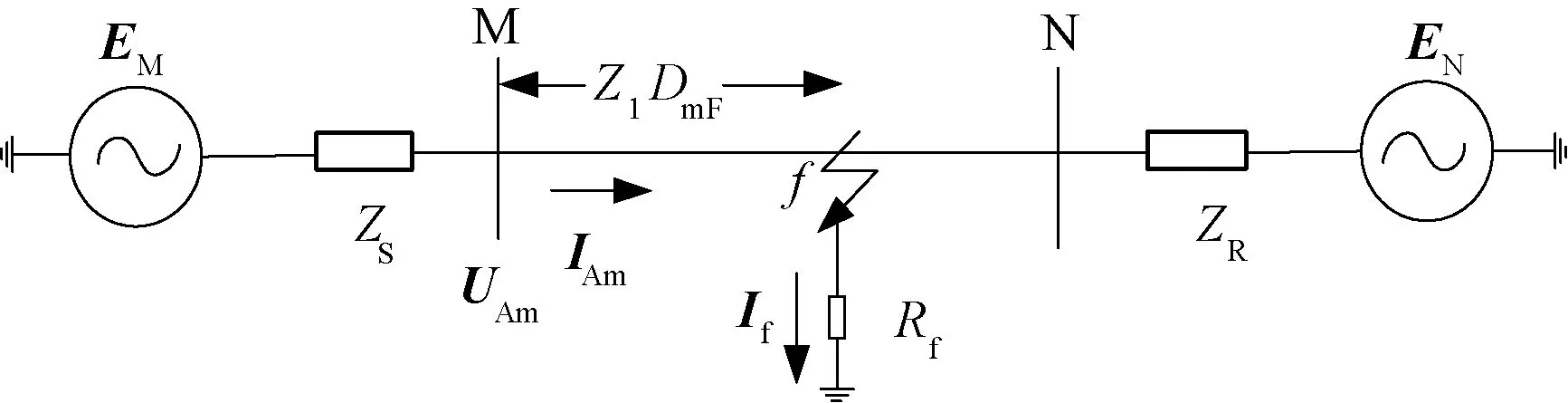
图1 A相线路接地故障Fig.1 Ground fault at A phase line

设M端为测量端，Z1、Cjm、Rf分别为线路单位长度正序阻抗、M端的序电流分布系数(j=0,1,2表示零序、正序、负序)、过渡电阻；Ijmg、IjmH、Ijf、I0m、DmF、k分别为M端序电流故障分量、序电流负荷电流、故障支路序电流、M端零序电流、故障距离、阻抗补偿系数。结合图1，由单相接地故障理论分析可知：

(1)

(2)

(3)

(4)

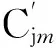
3 双馈风电场联络线单相接地故障特性

3.1 双馈风电场序阻抗特性

图2为含风电并网的双端电源系统。当风电场联络线K点发生单相接地故障时，风电场侧正负零序阻抗等值网络[10,11]如图3所示。图3中,Xm为风电机组励磁电抗；Xb和XT分别为箱变和主变电抗；s为转差率；故障期间，Rr和Rs分别为变化的定、转子电阻，Xr和Xs分别为变化的定、转子漏抗；受风电场变压器接线方式的影响，其零序网络中仅包含主变阻抗。

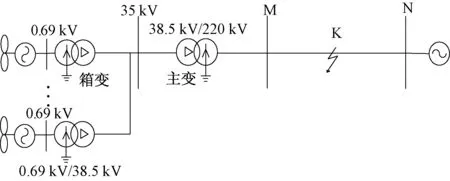
图2 风电场并网系统示意图Fig.2 Schematic diagram of wind farm integration system

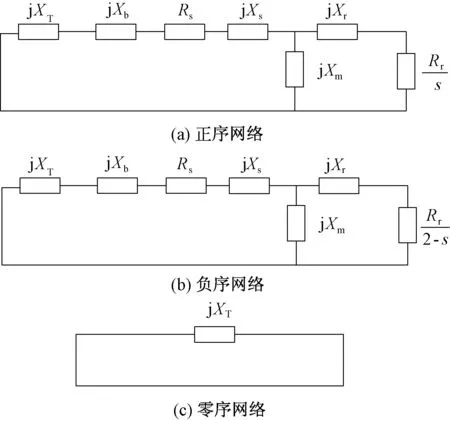
图3 风电场三序阻抗等值网络Fig.3 Equivalent three sequence impedance diagram of wind farm

由风电场侧正负序阻抗等值网络可知，双馈风电场正负序等值阻抗都包含风电场35/220kV主变、风电场内部35kV汇流线路、风电场0.69/35kV箱变与双馈风电机组的阻抗，且两者都受转差率s影响[12]。并且仍与双馈风电机组低电压穿越控制策略等因素有关[13]，同一双馈风电场的正负序等值阻抗随其运行方式变化而变化，正负序电流分布系数幅角γ1m与γ2m相应变化。图3(c)中风电场零序等值阻抗仅取决于主变电抗值，几乎不随风电场状态不同而改变，但风电场等值零序阻抗角与线路阻抗角和系统侧等值阻抗角都相差较大，同样会影响零序电流分布系数幅角γ0m大小。双馈风电场的正、负、零序等值阻抗在幅角和幅值上都不同于常规电源，由于风电场的接入，序电流分布系数幅角大小受到较大影响。若忽略幅角大小，将为测距带来更大误差。

3.2 双馈风电场联络线单相接地电流电压故障特性

根据图2，在PSCAD/EMTDC中搭建一双馈风电场并网的双端输电系统，此风电场装设18台1.5MV双馈风电机组，额定风速运行，经箱变由690V升压至35kV，多台机组汇集到一条长5km的集电线路，送至主升压变38.5kV/220kV,再经60km联络线并入系统。联络线参数为：Z1=0.4248∠85.3°Ω/km，Z0=1.181∠75.2°Ω/km；系统等值阻抗为：ZS1=60∠86.4°Ω,ZS0=30.8∠76.3°Ω，风电场主变参数为：变压器短路电压百分值Uk%=10.5%，额定容量SN=100MV·A。

对该系统进行单相(A相)接地故障特性分析，故障发生于风电场联络线，发生时刻1.5s，持续0.1s，算例采用文献[14]中的DFIG低电压穿越策略，避免了双馈风电场的偏频特性。风电场与系统侧短路电压电流波形如图4所示。

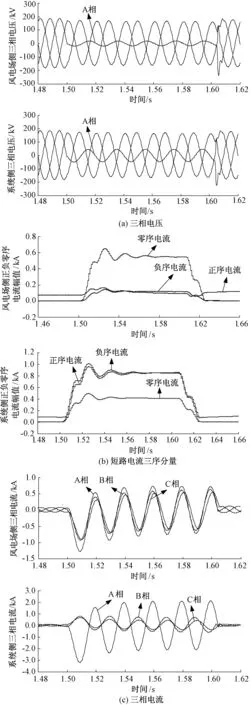
图4 风电场与系统侧短路电压、电流波形Fig.4 Short-circuit voltage and current waveforms of wind farm and system side

故障期间，图4(a)显示风电场侧与系统侧故障电压特性相似，由于发生单相接地故障，均是故障相电压跌落；从序分量角度分析，图4(b)表明与系统侧提供的短路电流三序分量相比，由于风电场等值零序阻抗远小于其等值正负序阻抗，导致风电场侧零序电流分量远大于正负序电流值，也使得图4(c)中风电场侧三相短路电流故障A相与非故障B、C相电流相位幅值相差不大,而系统侧则恰恰相反；相比于系统侧的等值阻抗，风电场侧的正负序等值阻抗要大很多，因此从图4(c)可以看出，风电场提供的短路电流远小于系统侧。而风电场容量又通常远小于被接入系统短路容量，由此可知，风电场表现出较为明显的弱电源性，并通过式(3)影响测距结果。

3）经费保障水平持续提高。2012年以来，国家财政性教育经费连续五年占GDP超过4%，其中一半以上用于义务教育，一半以上用于中西部。至2016年，中央财政累计投入1336亿元，带动地方投入2500亿元，其中52%用于义务教育。农村小学生均公用经费标准从10年前的10元提高到550元，初中由15元提高到750元。

4 双馈风电场联络线单相接地故障测距

4.1 风电场联络线单相接地故障测距分析

基于第2节的单相接地短路解复数方程故障测距原理，考虑到双馈风电场正负序等值阻抗在故障期间受多种因素影响表现不稳定，而零序等值阻抗较为固定，所以从风电场并网系统故障零序网(如图5所示)入手，进行风电场联络线单相接地故障测距分析。

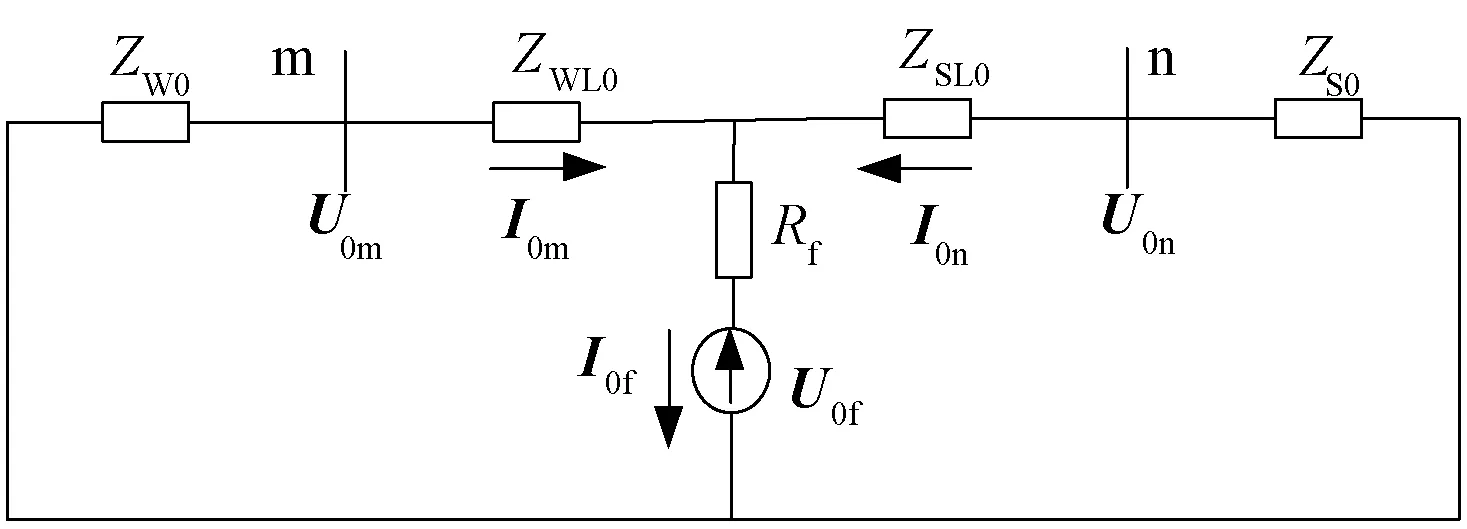
图5 风电场并网系统零序网络Fig.5 Zero sequence network of wind farm integration system

图5中，ZW0=RW0+jXW0,ZS0=RS0+jXS0，分别为风电场与系统零序等值阻抗；ZWL0,ZSL0为故障点距风电场侧与系统侧阻抗，且ZSL0=Z0DnF,ZWL0=Z0(DL-DnF),其中DL为两端系统间输电线路总长，DnF为故障点到系统侧的故障距离。以系统侧为测量端，测距公式为：

(5)

(6)

(7)

式中，C0n为系统侧测量端电流分布系数；γ0n为C0n幅角。

针对含双馈风电接入的双端输电系统，在风电场联络线发生单相接地故障期间，双馈风电场侧系统零序等值阻抗在幅角和幅值上与常规电源系统侧存在较大差异，这将严重影响序电流分布系数幅角大小。而这种影响则体现在系统侧零序电流与故障支路零序电流相位差和两端系统零序电流相位差变化上。若忽略幅角，测距精度将受到较大影响。

高压输电线路通常高电阻接地短路发生的概率较小[15]，本文针对低电阻接地情况展开研究，算例中Rf取10Ω，按常规线路测距方式视C0n为实数，则测量端分别在风电场侧与系统侧的测距结果如表1所示。

对高压输电线路一般相对误差要求不大于1%[1,4]。对表1分析可知，针对单相接地故障，在风电场联络线故障定位中忽视γ0n大小，风电场侧测距误差明显较大，远不符合工程要求；系统侧虽测距结果较好于风电场侧，但随着故障点越靠近风电场侧，由于受风电场联络线单相接地短路故障特性的影响，系统侧测距精度也显著下降。

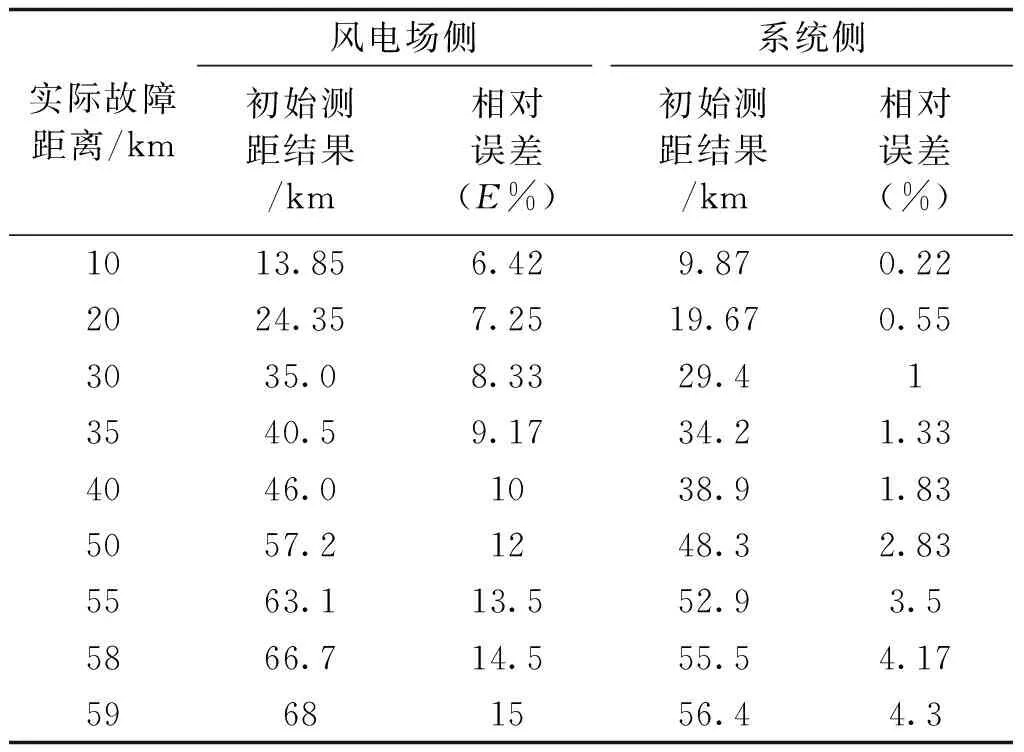
表1 双馈风电场联络线故障测距结果Tab.1 Fault location simulation results in tie-line with DFIG wind farm connecting

在不同的故障距离下，仿真研究两端系统零序电流相位差和测量端与故障支路零序电流相位差(取绝对值)，结果如图6和图7所示。

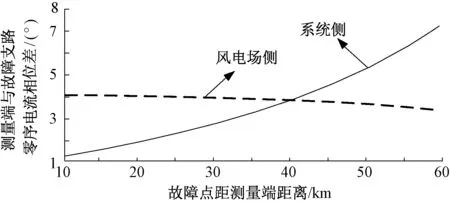
图6 测量端和故障支路零序电流相位差与故障距离关系Fig.6 Relation of fault distance and phase difference between zero sequence current of measuring end and fault branch

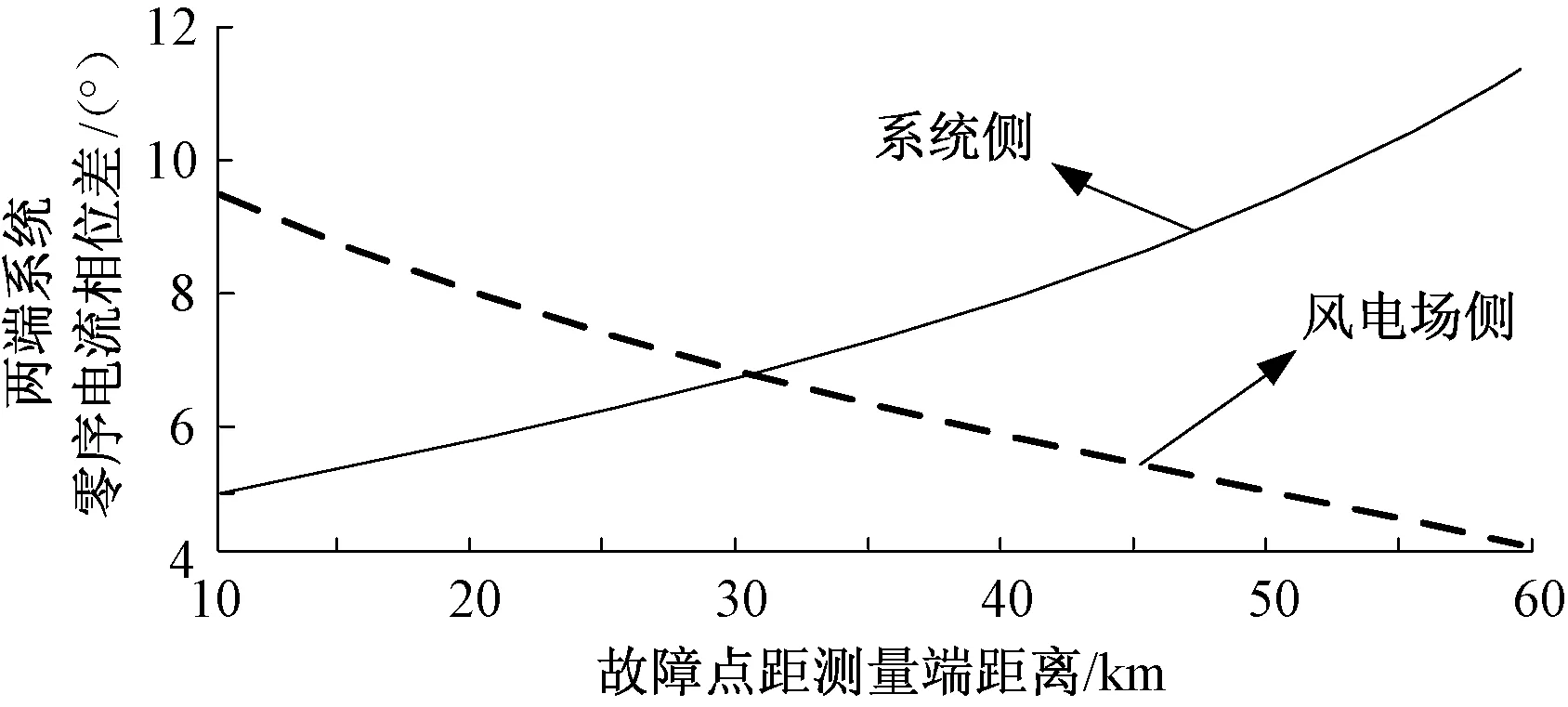
图7 两端系统零序电流相位差与故障距离关系Fig.7 Relationship between zero sequence phase difference of two sides system and fault distance

由图6和图7可以看出，无论是测量端在风电场侧还是系统侧，测量端和故障支路零序电流相位差与两端系统零序电流相位差整体都较大，并随着故障点越靠近风电场，两者数值成增长趋势。由于风电场侧等值零序阻抗角与线路阻抗角相差较大，故障点越接近风电场，由式(7)可知，这种差值对γ0n影响就越大，即对系统侧所测零序电流与故障支路零序电流相位差影响就越大，故障点越接近系统侧，这种影响就越小；由于系统侧等值阻抗角与线路阻抗角相差较小，风电场侧所测零序电流与故障支路零序电流相位差受故障距离的影响不大。

结合表1的测距结果可知，系统侧为测量端、故障距离小于30km时，系统侧零序电流与故障支路零序电流相位差较小，相对测距误差未达到1%，当故障距离再增大时相位差变大，测距误差也相应变大；在风电场侧为测量端时，所测零序电流与故障支路零序电流相位差都较大，测距误差都无法满足工程要求。显然不同于传统的两端电源系统，应用这种解复数方程测距原理已不能忽视C0n的幅角来近似测距。

另一方面，风电场因风速与投运机组数的变化，其输出的短路电流也会不同。为此同样以系统侧为测量端，研究风电场在不同风速和投运机组数的运行工况下，对测量端与故障支路零序电流相位差产生的影响，结果如图8和图9所示。

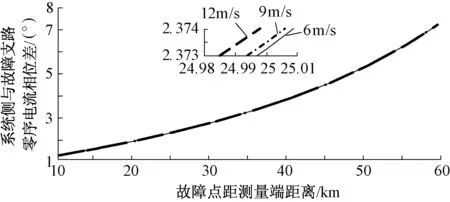
图8 测量端和故障支路零序电流相位差与风速关系Fig.8 Relation of wind speed and phase difference between zero sequence current of measuring terminal and fault branch

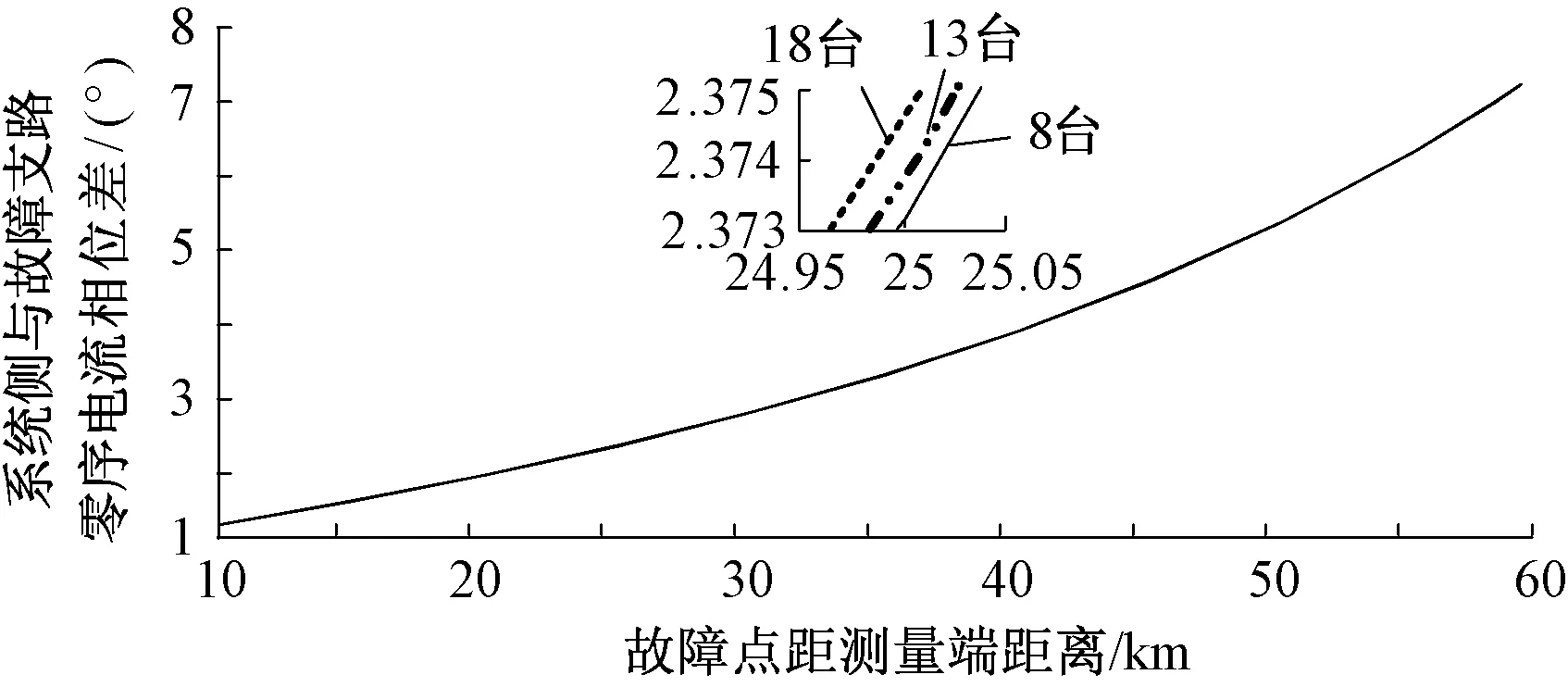
图9 测量端和故障支路零序电流相位差 与投运机组数关系Fig.9 Relation of number of DFIG in operation and phase difference between zero sequence current of measuring terminal and fault branch

仿真结果表明，风电场在不同运行方式下风速和投运机组数对测量端与故障支路零序电流相位差的影响很小。表明这种相位差更多取决于风电场联络线单相接地零序阻抗特性。

4.2 风电场联络线故障测距迭代补偿

基于4.1节分析可知，在双馈风电场并网的双端输电系统中，通过零序电流分配系数幅角补偿故障支路零序电流相位，可以优化测距结果。这里考虑到风电场联络线故障特性的特殊性，选用故障特征更为符合常规电源的系统侧作为测量端,采用4.1节的风电场并网算例。由式(7)可得，幅角γn0与故障距离DnF函数关系为：

(8)

在零序网络中，由于XS0R-XRS0>0，幅角γn0与故障距离DnF成增函数关系[1]。为此在计算故障距离时以Cn0为实数，计算出误差结果DnF0，代入式(8)，所得γn01用于补偿故障支路零序电流相位，并由式(5)求得DnF1，再代入式(8)，不断迭代补偿故障支路零序电流相位，而所测距离DnFn会不断向真实距离逼近，最终满足DnFn-DnF(n-1)<ε，迭代过程结束，从而提高了测距精度。表2为风电场联络线单相故障时对系统侧迭代补偿后的测距结果。相比表1，该方法减小了测距误差。

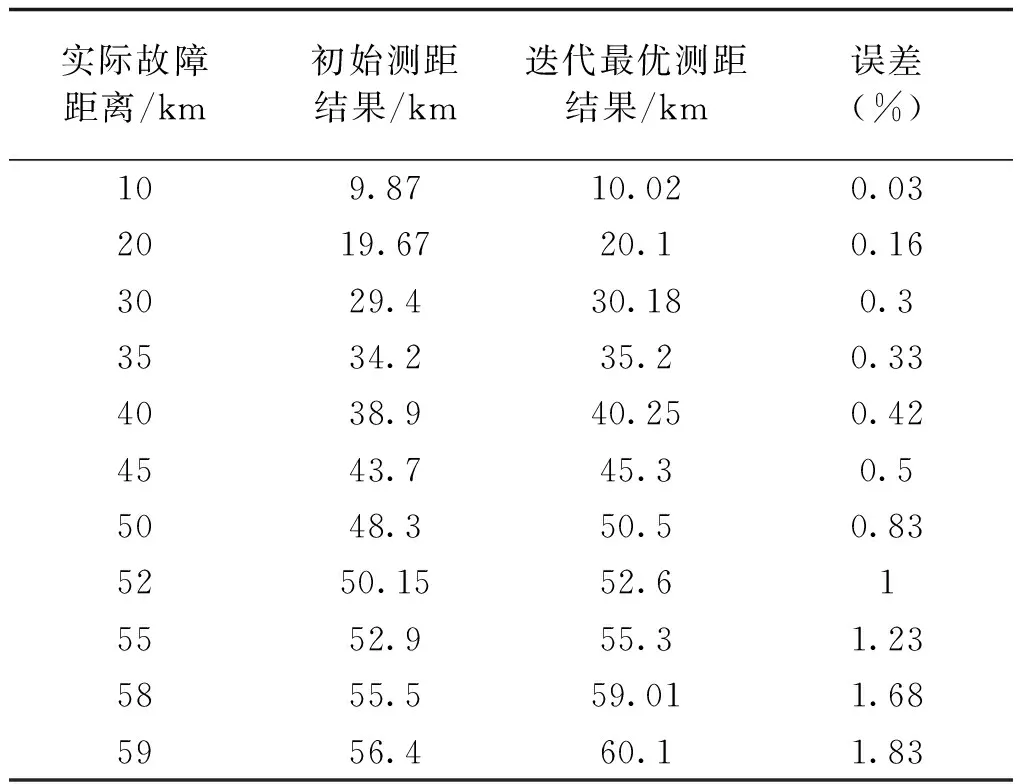
表2 系统侧迭代补偿后的测距结果Tab.2 Fault location final results after iterative compensation to initial results in system side

图10为通过迭代得到最终逼近真实值的故障距离所得的零序电流分布系数幅角，用于补偿故障支路零序电流相位。其中虚线为经迭代后故障距离为52km、测距误差达到1%时的分界线，在故障距离大于52km时，测距误差略大于1%，可见虽然整体上通过迭代补偿故障支路零序电流相位可有效提高测距精度，但故障点越接近于风电场这种迭代效果越有限。

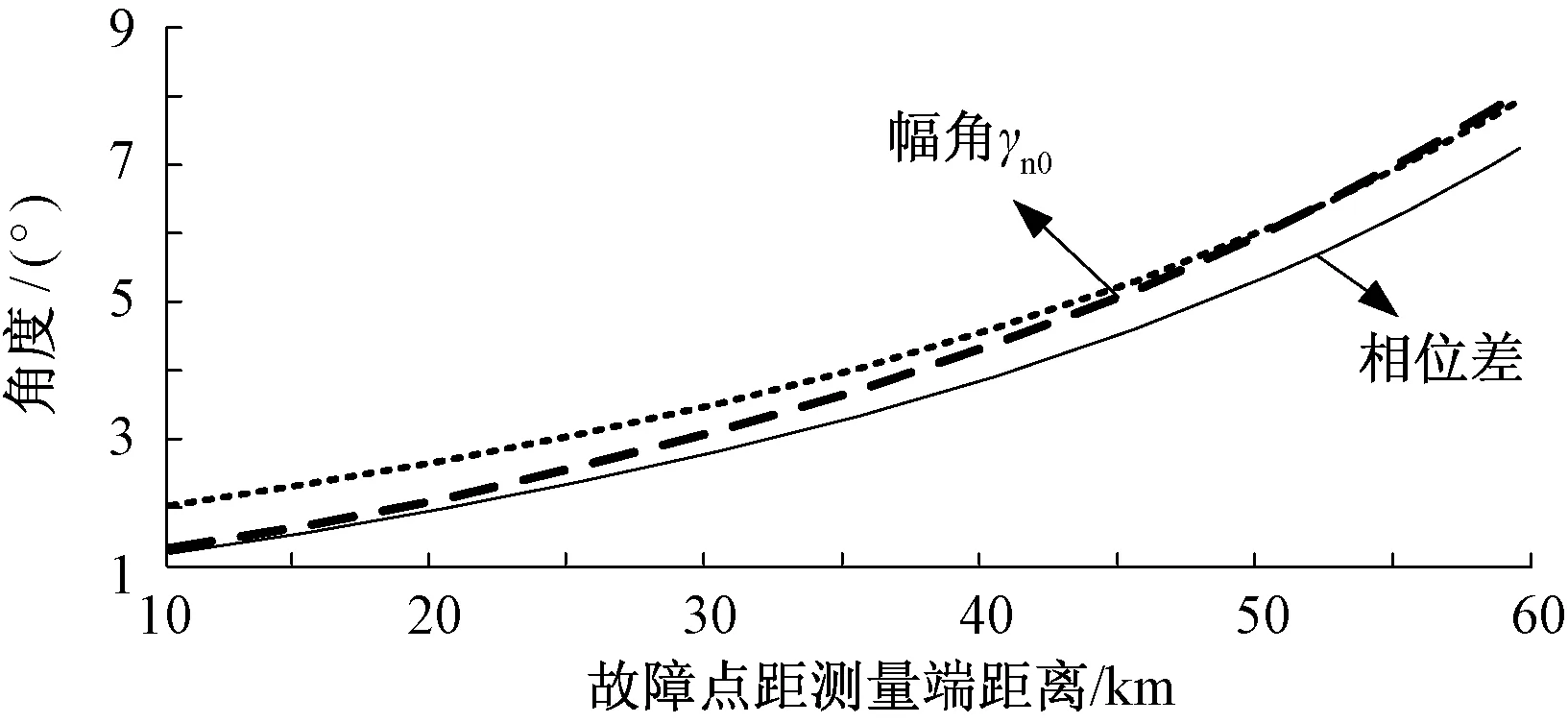
图10 γn0与测量端和故障支路零序 电流相位差的对比关系Fig.10 Comparison of γn0 and phase difference between zero sequence current of measuring terminal and the fault branch

5 结论

本文通过建模仿真研究了双馈风电场联络线单相接地故障时，风电场在序阻抗、短路电流、电压三方面的故障特性。基于零序网络，将传统解复数方程测距方法应用于双馈风电场联络线单相接地故障测距中，结果证明测量端无论在风电场侧还是系统侧测距误差都难以满足精度要求。进而结合风电场故障特性分析出导致测距误差的关键因素在于测量端与故障支路零序电流相位差。以故障特征更为接近常规电源的系统侧为测量端，证实了风电场运行风速和投入机组数对测量端与故障支路零序电流相位差值影响不大，并利用零序电流分布系数幅角γn0与故障距离DnF成增函数关系,通过迭代补偿故障支路零序电流相位，有效提高了测距精度。同时指出故障点越接近于风电场，这种迭代效果越有限。

[1] 葛耀中(Ge Yaozhong). 新型继电保护与故障测距原理与技术(The principle and technology of advanced relay protection and fault location)[M]. 西安:西安交通大学出版社(Xi’an: Xi’an Jiaotong University Press), 2007. 260-285．

[2] 哈恒旭, 王婧, 谭雨珍, 等(Ha Hengxu, Wang Jing, Tan Yuzhen, et al.). 基于微分算子逼近的单端故障测距新原理(New single-ended fault locating principle based on differential operator approach)[J].电力系统自动化(Automation of Electric Power Systems), 2009, 33(3): 69-73.

[3] 哈恒旭, 张保会, 吕志来(Ha Hengxu, Zhang Baohui, Lv Zhilai). 高压输电线路单端测距新原理探讨(A novel principle of single-ended line fault location technique for EHV transmission system)[J]. 中国电机工程学报(Proceedings of the CSEE), 2003, 23(2): 42-45.

[4] 黄小波(Huang Xiaobo). 基于分布参数模型的高压输电线路故障测距新算法研究(The research of fault location new algorithms based on the distributed parameter model for high voltage transmission line)[D]. 武汉：华中科技大学(Wuhan: Huazhong University of Science & Technology), 2007.

[5] 梁睿, 孙式想(Liang Ri, Sun Shixiang). 单端行波故障测距的组合方法研究(A combined method for single-ended traveling wave fault location)[J]. 电网技术(Power System Technology), 2013, 37(3): 699-706.

[6] 王宾, 董新洲, 薄志谦, 等(Wang Bin, Dong Xinzhou, Bo Zhiqian, et al.). 特高压长线路单端阻抗法单相接地故障测距(An impedance fault location algorithm for UHV long transmission lines with single-line-to-ground faults)[J]. 电力系统自动化(Automation of Electric Power Systems), 2008, 32(14): 25-29.

[7] 王茂清(Wang Maoqing). 基于阻抗法与行波法相结合的输电线路单端故障测距研究(Research on single-ended fault location based on combination of impedance method and traveling wave method)[D]. 北京：中国电力科学研究院(Beijing: China Electric Power Research Institute), 2010.

[8] 卢继平, 黎颖, 李健, 等(Lu Jiping, Li Ying, Li Jian, et al.). 行波法与阻抗法结合的综合单端故障测距新方法(Non-communication fault locating of transmission line based on traveling wave and impedance method)[J]. 电力系统自动化(Automation of Electric Power Systems), 2007, 31(23): 65-69.

[9] 王宾, 陆元园, 袁冰, 等(Wang Bin, Lu Yuanyuan, Yuan Bing, et al.). 双馈型风电场并网线路单端故障测距性能分析及改进(Performance analysis and improvement of single-terminal fault location in transmission lines with DFIG wind farm connecting)[J]. 电力科学与技术学报(Journal of Electric Power Science and Technology), 2015, 30(3): 4-10.

[10] 黄涛, 陆于平, 凌启程, 等(Huang Tao, Lu Yuping, Ling Qicheng, et al.). 撬棒电路对风电场侧联络线距离保护的影响及对策(Impact of crowbar on wind farm side interconnection line distance protection and mitigation method)[J].电力系统自动化(Automation of Electric Power Systems), 2013, 37(17): 30-36.

[11] F Sulla, J Svensson, O Samuelsson. Symmetrical and unsymmetrical short-circuit current of squirrel-cage and doubly-fed induction generations[J]. Electric Power Systems Research, 2011, 81(7): 1610-1618.

[12] 何倩(He Qian). 双馈风电场并网对联络线继电保护的影响及改善措施(Impact of doubly-fed wind power grid integration on transmission line relay protection and improvement measures)[D]. 北京：华北电力大学(Beijing: North China Electric Power University), 2014.

[13] 岳涵, 郑宽, 于洋, 等(Yue Han, Zheng Kuan, YuYang, et al.). 大规模双馈风电接入对东北电网稳定性的影响(Impact of large-scale DFIG based wind power on stability of northeast power grid)[J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2013, 32(4): 1-6, 20.

[14] 李凤婷, 陈伟伟, 樊艳芳, 等(Li Fengting, Chen Weiwei, Fan Yanfang, et al.). 基于电压跌落程度及变阻值的DFIG低电压穿越综合策略(A integrated control strategy for LVRT of DFIG based on voltage dip levels and dynamic resistance)[J]. 电网技术(Power System Technology), 2015, 39(12): 3408-3413.

[15] 王召磊(Wang Zhaolei). T型输电线路精确故障定位算法研究(Research on accurate fault location algorithm for T-type transmission lines)[D]. 北京: 北京交通大学(Beijing: Beijing Jiaotong University), 2015.

Analysis of single-terminal fault location in DFIG wind farm tie-line

XU Xiao-bin1, LI Feng-ting1, YUAN Bing2, LIU Jin-ying2,LIU Zong-jie2, ZHOU Wei-ji1

(1. Electrical Engineering College, Xinjiang University, Urumqi 830047, China;2. Jining Power Supply Company, State Grid Shandong Electric Power Company, Jining 272023,China)

The single phase to ground fault characteristics of wind farm tie line are affected strongly by wind farm operation mode, low voltage ride through (LVRT) strategy, and so on, so that traditional fault location methods cannot be applied to the wind farm tie line. According to a traditional fault location method of solving complex equation, impedance characteristics of doubly fed wind farm tie line was studied. Based on PSCAD/EMTDC, a simulation mode of doubly fed wind farm tie line were established, and its short circuit current and voltage characteristics were analyzed through simulation. Based on the zero sequence network of the doubly fed wind farm tie line, the key factor of introducing error when adopting the proposed method was indicated, the influences on the factor under different wind speed and different number of operating wind turbines were studied through simulation, and the accuracy of fault location was effectively improved by iterative compensating zero sequence current of the fault branch.

DFIG wind farm; single-phase earth fault; zero sequence network; fault location

2016-04-01

国家自然科学基金项目(51267019)

徐晓宾(1990-)， 男， 河北籍， 硕士研究生， 研究方向为可再生能源并网技术与电力系统继电保护； 李凤婷(1965-)， 女， 河北籍， 教授， 博导， 博士， 研究方向为间歇性源荷接入系统的运行控制与保护。

TM773

A

1003-3076(2017)01-0066-07