基于局域均值分解和支持向量数据描述的高压断路器机械状态监测

黄南天， 方立华， 王玉强， 赵振峰

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网冀北电力有限公司检修分公司， 北京 102488)

基于局域均值分解和支持向量数据描述的高压断路器机械状态监测

黄南天1， 方立华1， 王玉强2， 赵振峰2

(1. 东北电力大学电气工程学院， 吉林省 吉林市 132012； 2. 国网冀北电力有限公司检修分公司， 北京 102488)

为满足断路器机械状态监测的高可靠性要求，弥补现有方法易将轻微故障及无训练故障样本类型误识别为正常状态的不足，提出一种基于局域均值分解(LMD)能量熵和支持向量数据描述(SVDD)的高压断路器机械状态监测新方法。首先，利用LMD方法将断路器振动信号分解为一系列的PF(Product Function)分量，将各PF分量的包络按时间等间隔分段，并提取各PF分量包络的能量熵构成特征向量；然后，采用正常状态断路器振动信号的LMD能量熵向量训练SVDD分类器；最后，通过SVDD分类器对断路器的机械状态进行判断。实测信号实验证明，新方法比支持向量机(SVM)、BP神经网络(BPNN)等传统多类分类方法有更好的状态监测效果。

高压断路器； 机械状态监测； 局域均值分解； 能量熵； 支持向量数据描述

1 引言

高压断路器在保证电能质量和供电可靠性方面发挥着重要的作用，机械故障是影响断路器可靠性的最主要原因[1-3]，对断路器开展状态监测及故障诊断的研究具有十分重要的意义。而状态监测作为故障诊断的基础，可以提高断路器故障诊断结果的可靠性。因此，必须对状态监测给予足够的重视。

高压断路器在分合闸过程中产生的振动信号蕴含着丰富的机械故障信息，基于振动信号的状态监测是高压断路器机械状态监测最有效的方法之一[3-7]。文献[5]利用因子分析法对特征向量进行降维后输入支持向量机(Support Vector Machine, SVM)进行故障分类; 文献[6]对振动信号进行经验模态分解(Empirical Mode Decomposition, EMD)，并将本征模态函数分量(IMF)能量比作为特征向量输入神经网络开展分类；文献[7]提出利用小波包和改进特征熵处理振动信号，并将提取的特征熵向量输入BP神经网络(BP Neural Network, BPNN)实现故障分类，取得较好的效果。这些故障诊断方法能准确地判别有训练样本的故障类型，但未考虑到轻微故障类型和无训练样本的新类型故障对故障诊断结果的影响，仅将正常样本和3至4种常见故障类型样本作为训练样本，输入到多类分类器进行训练，之后开展故障分类。然而，传统多类分类器对训练样本表现出较大依赖性，需要大量故障样本作为支撑。高压断路器机械故障种类繁多，且高压断路器动作次数稀少，不可能通过实验得到全部故障类型，并且很多类型的故障样本获取成本较高，因而很难获得包含所有故障类型的训练样本，现有研究中均未将无训练故障类型作为分析对象[5-7]。由于缺乏训练样本，传统多类分类器很容易将一些训练样本中不包含的故障类型误识别为正常样本; 另外，传统多类分类方法的识别目标是实现正常样本与所有故障类型样本的综合识别准确率最高，而把任何一个新样本(无训练样本)预测为大类就可以获得很高的分类准确率，从而容易将无训练样本和轻微故障类型误识别为正常状态[4]。

传统多类分类器对训练样本的过度依赖，导致其状态监测能力有限。单类分类器只采用相对容易获得的正常状态样本即可完成训练[8,9]，克服了传统多类分类器对训练样本过度依赖的缺陷，因此非常适合用来对断路器进行状态监测，即判断断路器工作状态是否正常。现有的单分类方法中，由David M. J. Tax[9]提出的支持向量数据描述(Support Vector Data Description, SVDD)具有算法复杂性低，适合对高维度、小样本数据进行处理的优点，已经成功应用到状态监测领域[8]。

准确的特征描述是断路器机械状态监测的基础。现有时-频分析方法中，小波变换(Wavelet Packet Transform， WPT)和EMD等方法常被用来提取故障特征向量。这两种方法虽取得了不错的效果，但仍存在不足之处。小波分解不是自适应的信号处理方法，且在小波基和分解尺度的选定上需要做进一步的研究，分解过程中还会造成能量泄漏，影响分解结果[6]。EMD虽具有自适应性，但易出现过包络、欠包络以及模态混叠等问题[10-14]，且通过Hilbert变换来获取各IMF分量包络时会出现加窗效应，使解调结果出现较大误差；过多的“筛分”次数会导致端点效应，从而对整个数据段造成较大程度的污染[13]。这都会对特征提取产生严重的影响。

局域均值分解(Local Mean Decomposition，LMD)是J. S. Smith提出的一种自适应信号分解方法，可将非平稳信号自适应地分解为若干单分量纯调幅-调频信号(即PF分量)之和[11-13]。LMD与EMD方法相比，具有迭代次数更少、抑制端点效应、更加完整地保留信号信息等优点。不同类型振动信号的PF分量能量值具有显著差异，而能量熵可对振动信号的时-频能量分布进行定量描述，因此可以将LMD能量熵作为特征向量。

本文将LMD能量熵和SVDD理论相结合，提出一种高压断路器机械状态监测新方法。首先，用LMD方法将每一个原始信号分解为一系列的PF分量；之后，选取包含最有效故障信息的前5个PF分量，将各分量包络按时间等间隔分成M段并计算LMD能量熵；最后，用正常状态断路器振动信号的LMD能量熵作为训练样本训练SVDD，并实现状态监测。通过实测信号实验，并与SVM和BPNN作对比来验证新方法的有效性。

2 LMD分解原理

LMD方法的实质是将复杂的非平稳信号由高频到低频自适应分解成多个纯调频信号和包络信号的乘积，即PF分量[11-13]，通过多次迭代，得到该非平稳信号完整的时-频分布。其分解过程如下[13]：

(1)找出待分解信号x(t)的所有极值点pi，并对任意两相邻极值点pi和pi+1取平均值，因此，第i段的平均值即局域均值可以表示为：

(1)

用直线将式(1)求得的第i段和第i+1段的局域均值连接起来，并通过滑动平均法对其进行平滑处理，从而获得第一个局域均值函数m11(t)。

(2)第i段的包络估计值可以表示为：

(2)

用与步骤(1)同样的方法对获得的包络估计值进行处理，得到第一个包络估计函数a11(t)。

(3)把m11(t)从待分解信号x(t)中剔除，得到信号h11(t)：

(3)

(4)用h11(t)除以a11(t)，实现对h11(t)的解调，从而得到一个调频信号s11(t)，即

(4)

重复步骤(1)和步骤(2)，对获得的解调信号s11(t)求包络估计函数a12(t)。如果a12(t)等于1，则说明解调信号s11(t)是一个纯调频信号；否则，需要把解调s11(t)作为待分解数据迭代步骤(1)～步骤(4)q次，直到获得一个纯调频信号s1q(t)时迭代终止，此时包络估计函数a1(q+1)(t)等于1。因此，有

(5)

式中

(6)

迭代终止条件为：

(7)

但在实际分解过程中，要完全满足该迭代终止条件是不容易的，因此可设一个正增减量Δe，并使得a1q∈[1-Δe,1+Δe]时迭代终止。基于此判据，在保证分解精度的前提下，不仅使迭代次数减少，从而减轻端点效应的影响，而且缩短了运算时间。

(5)计算第一个PF分量的包络信号a1(t)，也即PF分量的瞬时幅值：

(8)

将式(8)得到的包络信号a1(t)与得到的纯调频信号s1q(t)相乘即可获得待分解信号x(t)的第一个PF分量，即

(9)

PF1(t)是待分解信号频率最高的单分量成分，它的瞬时频率f1(t)可以通过式(10)求得：

(10)

(6)将PF1(t)从待分解信号x(t)中剔除，从而获得一个新的信号u1(t)，将u1(t)作为待分解信号重复步骤(1)～步骤(4)分解过程，进行d次循环，直到ud(t)的极值点不超过1个时循环终止，此时ud(t)称为残余量。这样，待分解信号x(t)就被分解为d个PF分量和1个残余量ud(t)，即

(11)

从LMD的分解结果可以看出，该方法未丢失信号的任何信息，可以将多分量的断路器故障信号最终分解为若干单分量的调制信号，更加清晰地反映信号的内在信息和局部特征，有助于通过分析振动信号来实现高压断路器机械状态监测。

3 SVDD

SVDD作为一种单类分类方法，只用相对容易获得的正常样本即可完成分类器训练，判定是否发生故障。假设{xl,l=1,2,…,n}为输入空间的训练样本集，n为样本个数，SVDD的基本原理是在高维特征空间寻找一个球心为μ、半径为R的超球体，并使该超球体包含尽可能多的目标样本(正常样本)且体积最小[8,9]，如图1所示。

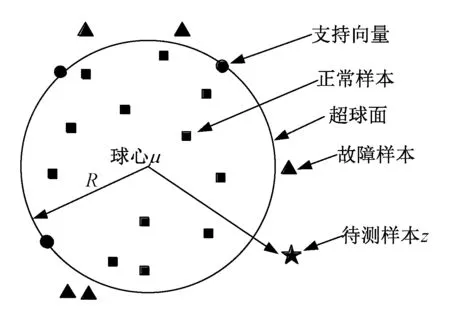
图1 SVDD原理图Fig.1 Sketch of SVDD algorithm

为了允许训练样本中存在异常值，引入变量ξl来惩罚背离超平面的异常点。SVDD可由式(12)来描述[8,9]：

(12)

式中，C用来实现错分样本数量与超球体体积之间的平衡；φ为非线性映射，将输入空间的样本xl映射为高维特征空间的φ(xl)。

对式(12)求对偶形式得到最优解，其形式为：

(13)

求解式(13)，对应拉格朗日乘子αl>0的样本xl即为支持向量。核函数K(xl,xk)=〈φ(xl),φ(xk)〉，表示特征空间中两个向量的内积。新方法采用径向基高斯核函数，其形式为：

(14)

式中，σ为径向基高斯核函数的宽度参数。

超球体的半径R可由超球体球心μ到任意位于超球面上的样本xs的距离来表示：

(15)

对任意待测断路器样本z(可能是已知类型，也可能是未知类型)，通过比较特征空间中球心到φ(z)的距离与半径R的大小，即可判断该样本是否为正常样本。决策公式为：

(16)

如果f(z)≤0，则说明该样本落在超球体内，为正常样本，否则为故障样本。

SVDD只用单类样本(正常样本)开展训练即可判定断路器状态，不受故障训练样本缺失问题的影响。因此，SVDD更适用于开展断路器状态监测。

4 特征提取与故障诊断流程

4.1 LMD能量熵

断路器振动信号的能量分布会随着频率的变化而发生变化。当断路器发生机械故障时，各PF分量中信号时-频能量分布相较正常状态振动信号能量分布产生明显变化。而能量熵可对振动信号的时-频能量分布进行定量描述，因此可以将LMD能量熵作为特征向量。

首先将分解得到的PF分量的包络按其时间特征平均分为M段，以刻画延时类故障能量的微弱变化，并计算每段包络的能量：

(17)

式中，a(t)为PF分量的包络；i=1,2,…,M。对每段包络信号的能量做归一化处理得到：

(18)

根据能量熵的基本原理，定义第j个PF分量包络的能量熵为：

(19)

4.2 故障诊断流程

(1)将采集到的振动信号进行LMD分解，获得一系列的PF分量。

(2)选取包含故障状态信息最多的前5个PF分量，将PF分量的包络按等时间间隔分为M段；计算所选取的PF分量包络的能量熵，获得信号的LMD能量熵特征向量为F=[H1,H2,H3,H4,H5]。

(3)采集断路器振动信号作为待测样本，按照步骤(1)和步骤(2)提取待测样本的特征向量，并通过训练好的SVDD分类器判断该待测样本是否为故障样本，从而实现状态监测。

5 实验数据来源与分析

本文将LW9-72.5型SF6高压断路器作为研究对象。采用CA-YD-182A型压电式加速度传感器和美国国家仪器(NI)公司的NI9234数据采集卡搭建振动信号采集系统，信号采样频率为25.6kS/s。振动信号采集系统如图2所示。

图2 振动信号采集系统Fig.2 Vibration signal acquisition system

实验模拟合闸线圈铁心卡涩(故障I)、拐臂润滑不足(故障II)和断路器基座螺丝松动(故障III)3种断路器故障类型。其中，故障I和故障III为中等程度故障类型，故障II为轻微故障类型。正常状态及3种故障状态信号的振动波形如图3所示。

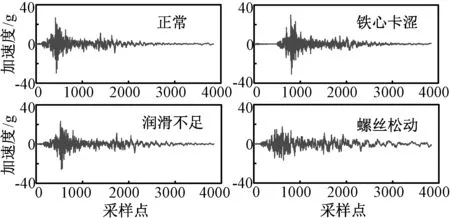
图3 实测信号振动波形Fig.3 Measured vibration signals waveform

5.1 基于LMD的信号分解方法

为了验证LMD分解方法的性能，取正常状态振动信号分别进行EMD和LMD分解，两种方法的分解结果如图4所示。

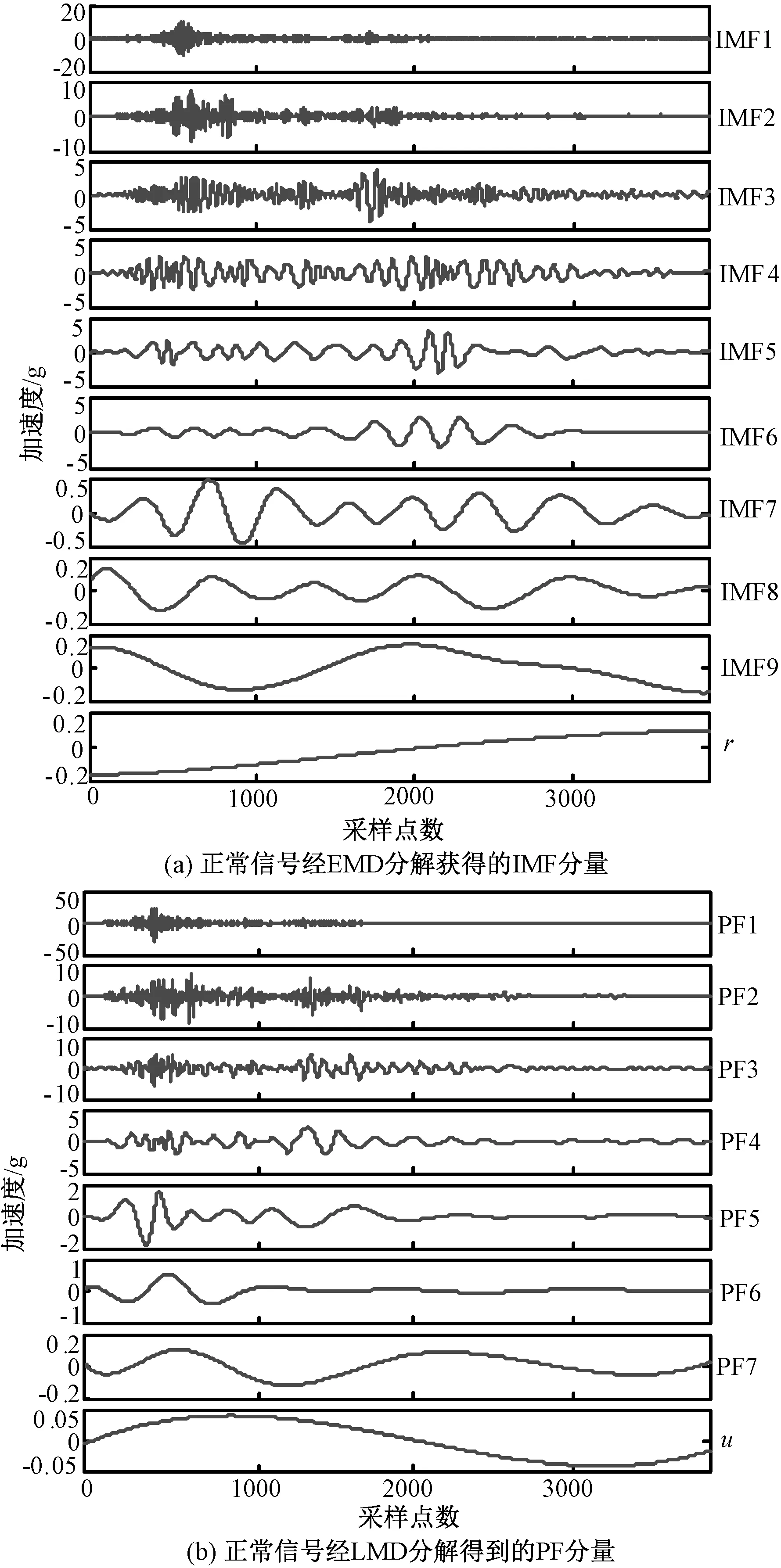
图4 LMD和EMD分解结果对比Fig.4 Comparison between decomposition results of LMD and EMD

从图4的分解结果可以看出，LMD分解所得到的分量个数要少于EMD，从而避免出现若干个分解水平相近、含有类似特征信息的分量，保证分解的效率和精度。为了对LMD方法的分解效果进行定量评定，以LMD和EMD分解同一振动信号前后的能量变化(即分解前后信号的均方根有效值与原始信号的均方根有效值的关系)作为评价指标评定两种方法的分解效果[12]。评价指标的公式为：

(20)

式中，θ表示分解前后原始信号的能量变化量，在此作为分解效果的评价指标；RMSPFm、RMSu、RMSx分别表示PF分量、残余分量ud以及原始信号x(t)的均方根有效值。其中原始信号x(t)的均方根有效值可以表示为：

(21)

式中，f表示采样点数，f=1,2,…,T。

根据定义可知θ≥0，θ值越大，表明分解前后信号能量变化越大，分解结果受端点效应的影响越大，分解精度也就越低。

取5组正常信号测试LMD和EMD的分解性能。表1给出了5组测试信号经过LMD和EMD分解后所得分量个数、分解时间和评价指标的平均值。

表1 LMD和EMD方法分解结果对比Tab.1 Contrast of LMD and EMD decomposition result

由表1可知，LMD方法分解得到的分量个数少于EMD，从而LMD方法分解的效率及精度高于EMD。从分解所需时间来看，LMD方法所需分解时间要少于EMD方法，这是由于EMD分解过程中每次迭代都通过三次样条函数插值来拟合形成上下包络线[10]，从而大大增加了时间开销。从评价指标来分析，LMD方法得到的θ值更小，即LMD分解前后信号的能量值变化更小，说明LMD方法可在一定程度上减轻端点效应的影响。

5.2 LMD能量熵特征向量提取

首先对图3的4种信号进行LMD分解，得到一系列的PF分量，通常LMD方法分解得到的前几个PF分量几乎包含了原始信号的全部能量。故障时-频特征主要体现在含有主要能量成分的PF，为此，本文以PF分量所含能量占原始信号能量的百分比(即能量比)为标准选取PF分量[11]。为增强实验结果的说服力，每种信号选择5组，并计算各PF能量比的平均值。4种信号各PF的能量比分布如图5所示。

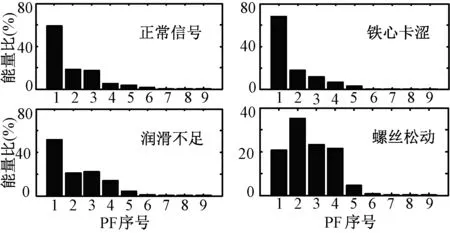
图5 4种信号各PF分量能量分布图Fig.5 Energy distribution of PFs obtained from four types of signals

由图5可以看出，4种断路器振动信号的前5个PF分量所含能量占原始信号能量的90%以上，因此选取每种信号的前5个PF分量；然后，根据实验分析，将各个PF分量的包络信号按时间等间隔分成20段；最后通过式(17)～式(19)计算各PF分量包络的能量熵，从而构成能量熵特征向量。表2中仅列出对每种信号所提取的3组LMD能量熵特征。

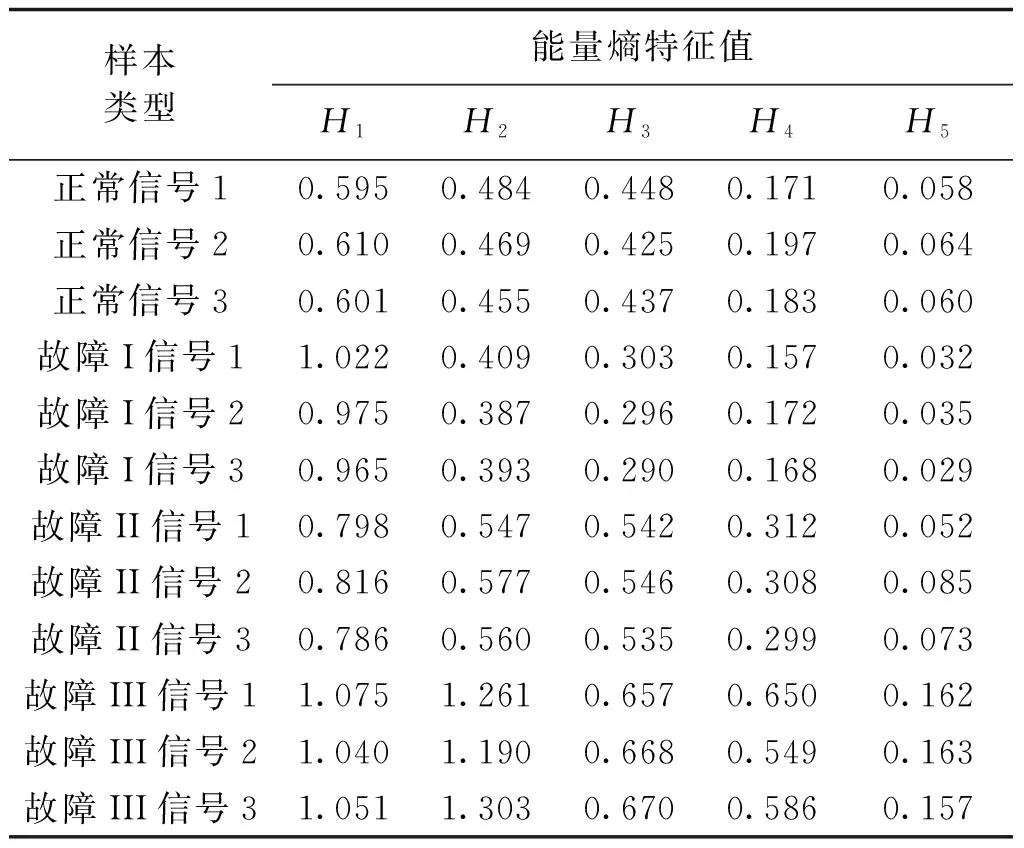
表2 LMD能量熵向量Tab.2 Vectors of LMD energy entropy

从表2可以看出，同类样本之间的熵值分布比较接近，而不同类样本之间的熵值分布差别较大；正常状态信号各PF分量的能量熵值分布比故障信号熵值分布均匀，这是因为断路器出现故障时，各机械结构的振动频率会发生变化，故障信号在各频带的能量分布也会出现较大差异。因此，可以根据该LMD能量熵向量来判断断路器是否发生机械故障。

5.3 基于SVDD的机械状态监测

为验证本文所提出状态监测方法的有效性，将SVDD与常用的SVM、BPNN分类器的状态监测结果作对比，用状态判别准确率来反映3种方法区分正常与故障样本的能力。实验中，采用20组正常状态信号作为SVDD分类器的训练样本，采用20组正常状态信号以及铁心卡涩(故障I)、基座螺丝松动(故障III)故障样本各20组作为SVM和BPNN分类器的训练样本。为比较3种分类方法对无训练样本类型的判别准确率，机械润滑不足(故障II)故障样本仅作为测试样本测试分类器性能而不用于训练分类器。另采集正常状态和3种故障状态样本各10组作为测试样本。3种方法的状态监测结果如表3和表4所示。

由表3和表4可以看出，对于有训练样本类型和无训练样本类型，SVDD的状态判别准确率都要高于SVM和BPNN。这是因为SVDD仅仅以正常样本为训练样本，相较于传统多分类器，SVDD状态监测结果不受无训练样本的新故障类型影响，能准确地将轻微故障类型和无训练故障样本类型判别为故障状态，可以满足断路器状态监测领域的高可靠性要求。但是，SVM、BPNN等传统多类分类器虽然可以准确识别有训练样本的具体故障类型，但在识别无训练样本的新故障类型方面具有明显劣势。因此，本文新方法更加适用于难以获得全部故障类型训练样本的实际电力系统断路器状态监测领域。

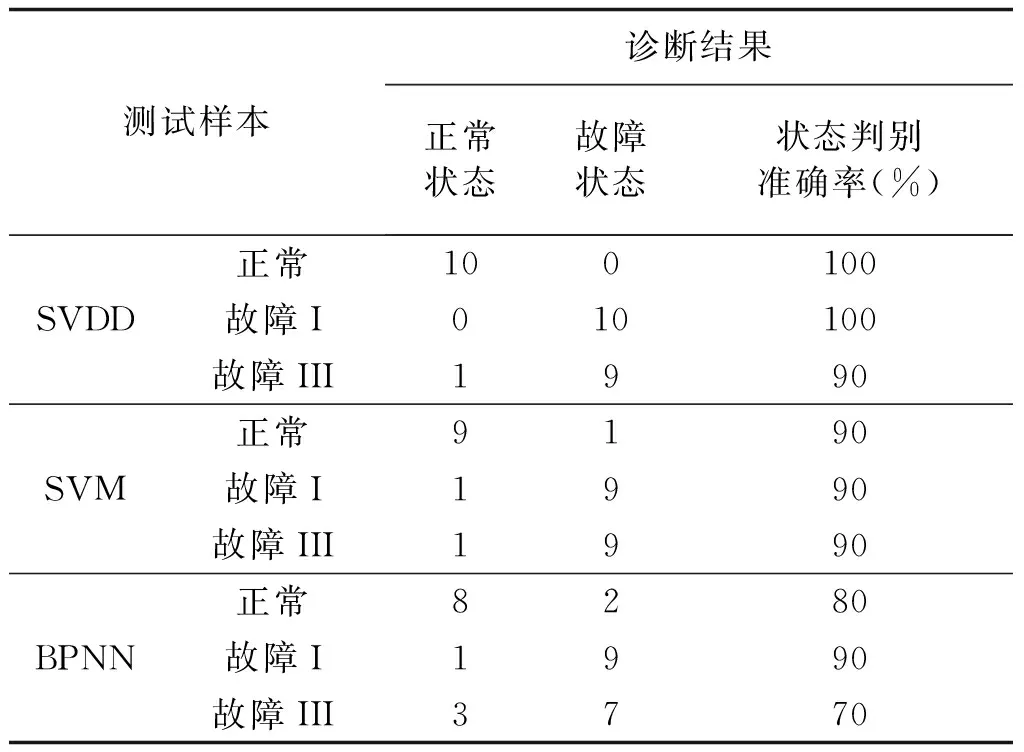
表3 有训练样本类型判别结果Tab.3 Discriminant results of patterns contained in training samples

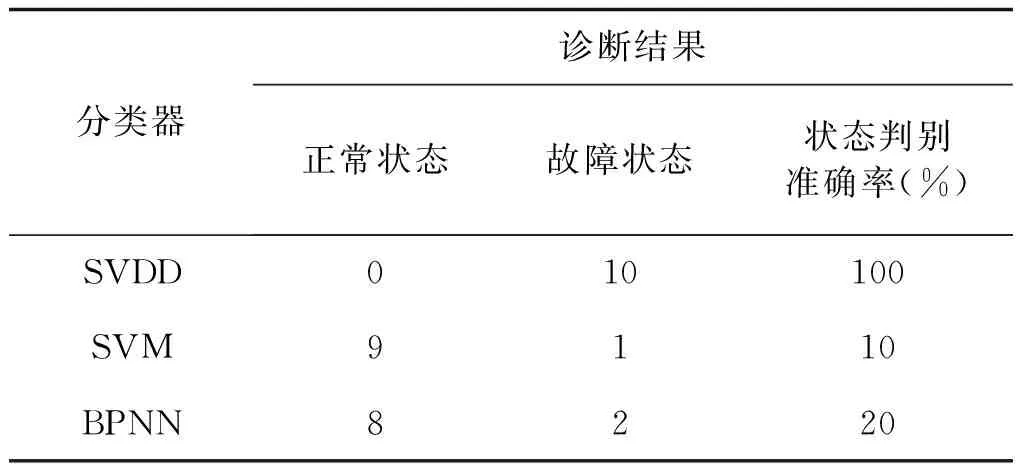
表4 无训练样本类型判别结果Tab.4 Discriminant results of patterns not contained in training samples

6 结论

本文提出一种基于LMD能量熵和SVDD的断路器机械状态监测新方法。首先对断路器振动信号进行LMD分解得到一系列PF分量，然后计算各PF分量包络的能量熵，并以此作为特征向量训练SVDD，并用训练好的SVDD判断设备状态。通过实测信号实验证明，新方法具有以下优点：

(1)新方法采用的LMD方法比EMD方法得到的模态数量少，分解速度快，并以分解前后信号的能量变化作为评价指标，证明LMD方法的分解效率及分解精度更高，并能在一定程度上抑制端点效应的影响。

(2)SVDD分类器克服了传统多类分类器易将轻微故障样本和无训练样本误识别为正常样本以及对训练样本要求高的缺陷，满足断路器机械状态监测的需要。

未来工作将集中于积累更多的实测振动信号和SVDD参数改进，以便进一步提升新方法的状态监测能力，并为未来开展故障诊断积累数据。

[1] M Landry, F Léonard, C Landry, et al. An improved vibration analysis algorithm as a diagnostic tool for detecting mechanical anomalies on power circuit breakers [J]. IEEE Transactions on Power Delivery, 2008, 23 (4): 1986-1994.

[2] A A Razi-Kazemi, M Vakilian, K Niayesh, et al. Circuit-breaker automated failure tracking based on coil current signature [J]. IEEE Transactions on Power Delivery, 2014, 29 (1): 283-290.

[3] 常广,王毅,王玮 (Chang Guang, Wang Yi, Wang Wei). 采用振动信号零相位滤波时频熵的高压断路器机械故障诊断 (Mechanical fault diagnosis of high voltage circuit breakers utilizing zero-phase filter time-frequency entropy of vibration signal) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2013, 33 (3): 155-162.

[4] 黄南天,张书鑫,蔡国伟, 等 (Huang Nantian, Zhang Shuxin, Cai Guowei, et al.). 采用EWT和OCSVM的高压断路器机械故障诊断 (Mechanical fault diagnosis of high voltage circuit breakers utilizing empirial wavelet transform and one-class support vector machine) [J]. 仪器仪表学报 (Chinese Journal of Scientific Instrument), 2015, 36 (12): 2773-2781.

[5] 程序, 关永刚, 张文鹏, 等 (Cheng Xu, Guan Yonggang, Zhang Wenpeng, et al.). 基于因子分析和支持向量机算法的高压断路器机械故障诊断方法 (Diagnosis method on the mechanical failure of high voltage circuit breakers based on factor analysis and SVM) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2014, 29 (7): 209-215.

[6] 缪希仁, 吴晓梅, 石敦义, 等 (Miao Xiren, Wu Xiaomei, Shi Dunyi, et al.). 采用HHT振动分析的低压断路器合闸同期辨识 (Switching synchronism identification of low voltage circuit breaker utilizing HHT analysis to vibration signal) [J]. 电工技术学报 (Transactions of China Electrotechnical Society), 2014, 29 (11): 154-161.

[7] 孙来军, 胡晓光, 纪延超 (Sun Laijun, Hu Xiaoguang, Ji Yanchao, et al.). 改进的小波包-特征熵在高压断路器故障诊断中的应用 (Fault diagnosis for high voltage circuit breakers with improved characteristic entropy of wavelet packet) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2007, 27 (12): 103-108.

[8] G N Li, Y P Hu, H X Chen, et al. An improved fault detection method for incipient centrifugal chiller faults using the PCA-R-SVDD algorithm[J]. Energy and Buildings, 2016, 116: 104-113.

[9] D M J Tax, R P W Duin. Support vector domain description [J]. Pattern Recognition Letters, 1999, 20 (11-13): 1191-1199.

[10] 游子跃,王宁,李明明, 等 (You Ziyue, Wang Ning, Li Mingming, et al.). 基于EEMD和BP神经网络的风机齿轮箱故障诊断方法 (Method offan fault diagnosis of gearbox based on EEMD and BP neural network) [J]. 东北电力大学学报 (Journal of Northeast Dianli university), 2015, 35(1): 64-72.

[11] H H Liu, M H Han. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings [J]. Mechanism and Machine Theory. 2014, 75 (5): 67-78.

[12] 韩晓慧, 杜松怀, 苏娟, 等 (Han Xiaohui, Du Songhuai, Su Juan, et al.). 基于局部均值分解的触电故障信号瞬时参数提取 (Extraction of biological electric shock signal instantaneous amplitude and frequency based on local mean decomposition) [J]. 农业工程学报 (Transactions of the Chinese Society of Agricultural Engineering), 2015, 31 (17): 221-227.

[13] 李纯子, 陈峰, 刘书成, 等 (Li Chunzi, Chen Feng, Liu Shucheng, et al.). 基于小波变换和LMD算法的变压器振动信号分析 (Analysis of transformer vibration signal based on wavelet transform and LMD algorithm) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2013, 32 (4): 69-73.

[14] Y Li, M Xu, R Wang, et al. A fault diagnosis scheme for rolling bearing based on local mean decomposition and improved multi-scale fuzzy entropy [J]. Journal of Sound & Vibration, 2016, 360: 277-299.

Machinery condition monitoring of high voltage circuit breakers based on local mean decomposition and support vector data description

HUANG Nan-tian1, FANG Li-hua1, WANG Yu-qiang2, ZHAO Zhen-feng2

(1. School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China;2. Maintenance Branch, State Grid Jibei Electric Power Co. Ltd., Beijing 102488, China)

In order to overcome the existing shortage of misidentification for the minor fault states and the fault patterns without training samples, a new method based on local mean decomposition (LMD) energy entropy and support vector data description (SVDD) was proposed to satisfy the high reliability of the machinery condition monitoring of high voltage circuit breakers. Firstly, the vibration signal of high voltage circuit breaker was decomposed into a set of product functions (PFs) by LMD. The segmental envelop energy entropy of PF based on the method of equal time interval was extracted to form feature vectors. Secondly, the LMD energy entropy vector of normal state signal was used to train SVDD classifier. Finally, SVDD was used to judge the machinery condition of high voltage circuit breaker. The experimental results show that the new method achieved better effect of condition monitoring in comparison with traditional multi-class classifiers such as support vector machine and BP neural network.

high voltage circuit breaker; machinery condition monitoring; LMD; energy entropy; SVDD

2016-03-22

国家自然科学基金项目(51307020)、 吉林省科技发展计划项目(20150520114JH)

黄南天(1980-)， 男， 吉林籍， 副教授， 硕导， 博士， 研究方向主要为电能质量分析、 新能源并网技术及电力设备状态监测等； 方立华(1992-)， 男， 山东籍， 硕士研究生， 研究方向为电力设备状态监测及故障诊断。

TM744

A

1003-3076(2017)01-0073-08