变论域模糊PID控制在改善DC-DC变换器非线性非最小相位系统的性能研究

杨 超， 苑 红， 余岱玲， 丁新平

(青岛理工大学自动化工程学院， 山东 青岛 266520)

变论域模糊PID控制在改善DC-DC变换器非线性非最小相位系统的性能研究

杨 超， 苑 红， 余岱玲， 丁新平

(青岛理工大学自动化工程学院， 山东 青岛 266520)

除Buck电路外的传统DC-DC电路的动态模型是非线性非最小相位系统，其动态特性受电路参数和动态模型的影响较大。PID控制必须建立在精确的数学模型上，而DC-DC变换器的非线性决定了PID调节很难达到更优的效果。模糊PID控制不需要精确的数学模型，而且消除了模糊控制存在的静差。但该控制方式的自适应能力较低，在输入量变化较大时，其控制精度变差。变论域模糊PID控制利用伸缩因子使系统的自适应能力提高，并增加模糊规则的利用率，使控制精度提高。本文研究了变论域模糊PID控制在非线性非最小相位系统的DC-DC变换器闭环控制中的性能，以DC-DC变换器中的典型非线性非最小相位系统的Sepic电路和Boost电路为例进行了仿真和实验,结果表明变论域模糊PID控制比前两种控制方式具有更优的控制性能。

变论域模糊PID控制； 非最小相位系统； DC-DC变换器； 伸缩因子

1 引言

DC-DC变换器具有高效率、高功率密度和高可靠性等优点，广泛应用于光伏发电、新能源应用和工业设备等领域，研究其性能改善和控制策略优化是一个热点。DC-DC转换器是一个非线性的时变复杂系统，难以精确地控制DC-DC转换器的转换[1]。而且DC-DC开关变换器中除Buck变换器及其衍生拓扑外，其余的如Boost、Buck-Boost、Cuk、Sepic、Zeta及其衍生拓扑都是非最小相位系统[2]。即当采用电容电压作为输出反馈控制时，变换器的数学模型是一个非最小相位系统，表现为小信号数学模型中存在复平面右半平面的一个零点[3]，该零点使得系统的动态品质变差，降低系统的稳态性能。

DC-DC变换器的闭环控制中常采用PID控制方式，该控制方式依赖于被控对象的精确数学模型[4]，技术成熟，控制效果好，但DC-DC变换器的非线性特性以及电路寄生参数影响了PID控制的精度和鲁棒性。而模糊PID控制解决了对被控对象数学模型的严苛依赖，通过模糊控制规则库对PID的参数进行在线调整，使被控系统的控制精度提高、鲁棒性增强、动态品质更好[5]。但对于复杂非线性系统，获取完整的控制规则库比较困难，致使模糊控制器难以满足高精度控制要求[6]。而且控制系统的模糊规则一旦确定，其结构就不能在线修改，因而自适应能力有限[7]。

文献[8]首次提出了变论域模糊控制的思想，即模糊规则一定的条件下，通过伸缩因子实现模糊论域的伸缩变化，间接地增加了模糊规则，提高了控制系统的动态品质和控制精度。因此可以将变论域的控制方式引入模糊PID控制中，通过在模糊部分增加变论域伸缩因子构成变论域模糊PID控制[9]，以提高控制系统对扰动的自适应能力，并改善被控系统的动态品质。

本文研究了非线性非最小相位系统的DC-DC变换器的变论域模糊PID控制，为了使研究更具有针对性和定量化，以应用较广泛的升降压型Sepic变换器和升压型Boost变换器为例进行研究。经仿真和实验验证，该控制方式比PID控制和模糊PID控制表现出更强的抗干扰能力和自适应能力，被控系统的动态品质和稳态精度更高。

2 变论域模糊控制器

2.1 模糊控制器设计

模糊控制器设计成两输入三输出的模式，模糊输入是误差(x)和误差变化率(y)，而输出是PID三个参数的调整值，即比例(ΔKp)、积分(ΔKi)和微分(ΔKd)。误差和误差变化率的模糊论域划分分别为：{-3,-2,-1,0,1,2,3}，{-8,-5,-2,0,2,5,8}，输出论域划分相同为：{-1,-0.6,-0.3,0,0.3,0.6,1}。模糊控制器的模糊规则见表1，其中的E和EC分别为误差和误差变化率的模糊论域值。

表1 模糊规则Tab.1 Fuzzy rules

2.2 变论域模糊PID控制器设计

在模糊PID控制器模糊部分，加上论域伸缩因子构成变论域模糊PID控制器，变论域模糊PID控制的结构框图如图1所示。式(1)和(2)分别为本文使用的输入论域伸缩因子α(x)和输出论域伸缩因子β(x)，其中E为误差论域值，EC为误差变化率的论域大小，x和y分别为误差和误差变化率，τ、τ1和τ2都为0到1之间的常数，ε为充分小的正数：

(1)

(2)

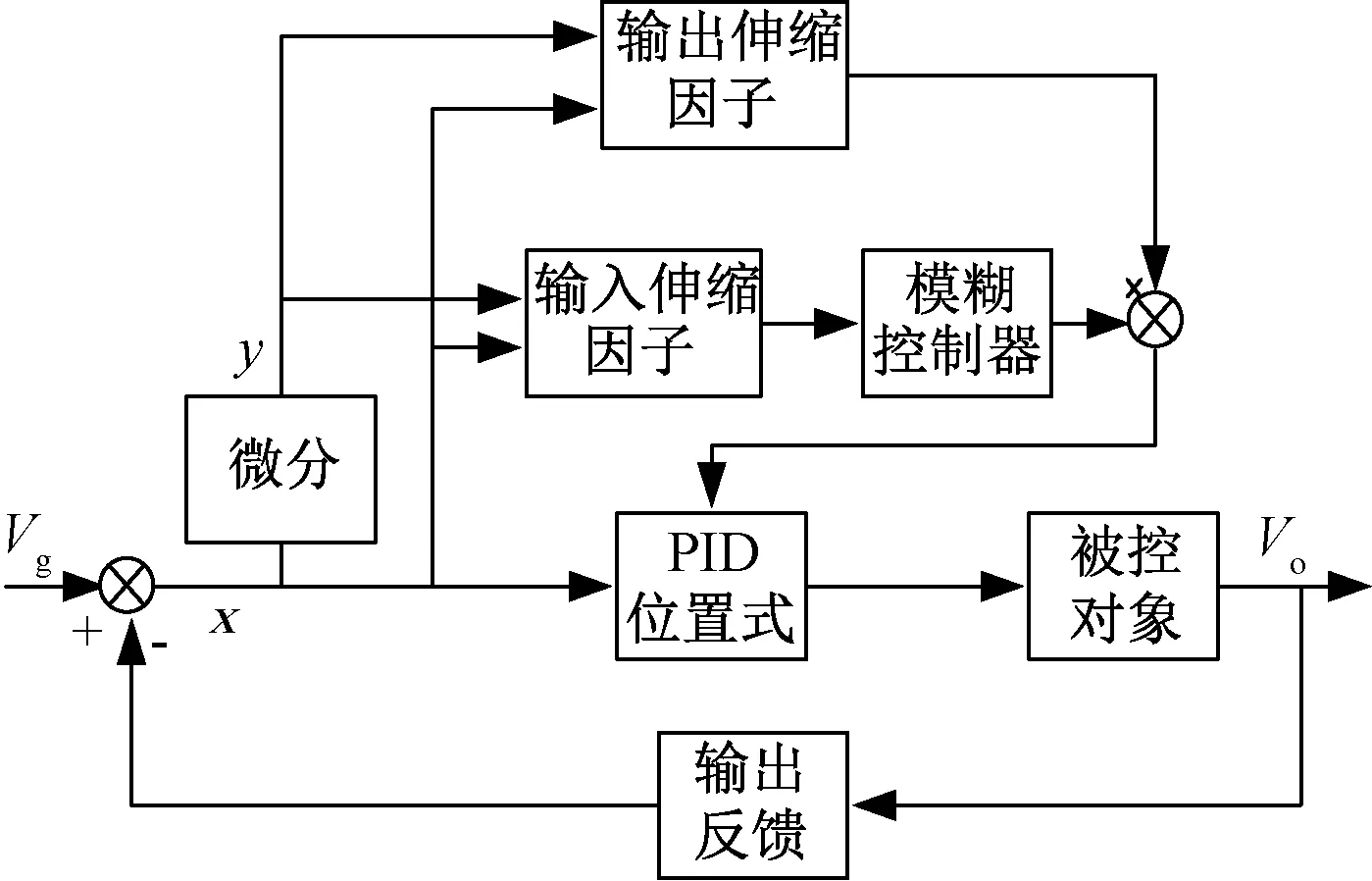
图1 变论域模糊PID控制的结构图Fig.1 Variable universe fuzzy PID control structure

2.3 变论域原理与伸缩因子

变论域模糊控制就是在模糊控制器的输入和输出部分添加论域伸缩因子，通过论域伸缩因子的调节，任意大小的输入都能对应到整个输入论域，因此在模糊规则不改变的条件下，变论域模糊控制通过论域伸缩因子实现了模糊规则的增加，并使系统的控制精度提高。变论域的原理如图2所示，E是误差论域值，α1(x)、α2(x)是伸缩因子，x∈[-E，E]，x是输入误差，μ为隶属度。

图2 变论域原理Fig.2 Principle of variable universe

伸缩因子可以定义为根据当前控制指标值对语言控制变量论域的调整[10]。对于伸缩因子α(x)函数的构造，应满足一些条件[11]，其中论域值X∈[-E，E]：

(1)对偶性：(∀x∈X)，有α(x)=-α(-x)成立。

(2)避零性：α(0)=ε，ε为充分小的正数。

(3)单调性：α(x)在[0，E]上严格单调递增。

(4)协调性：∀x∈X，x≤α(x)E。

(5)正规性：α(±E)=1。

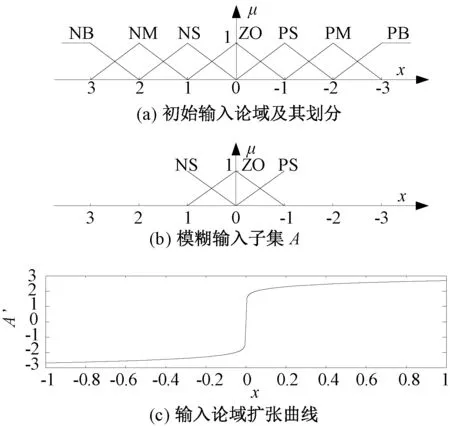
图3 输入论域变化曲线Fig.3 Changing curve of input universe

3 Sepic电路和Boost电路小信号模型及PID校正

3.1 Sepic电路

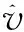
(3)

式中

k1=(rC1-rgs)IL1+rgsIL2+VC1+VC2+Vd

k2=rgsIL1-(rgs+rC1)IL2-VC1-VC2-Vd

k3=IL2-IL1

k4=rL1+Drgs+(1-D)rC1

k5=rL2+(rgs+rC1)D

k6=R{k3D[k4+(1-D)rgs]- [k2(1-D)+k1D](1-D)}

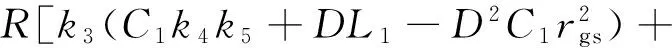
k8=RC1[k3(L1k5+L2k4)+ (k1L2-k2L1)(1-D)]

k9=(R+k5)(1-D)2+D2k4+2D2(1-D)rgs

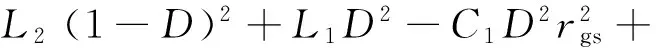
k12=C1(L1L2+C2L1Rk5)+C2L2Rk4

建立Sepic电路的闭环控制系统，系统的开环回路增益函数Go(s)为：

(4)

式中，H(s)、Gm(s)分别为系统反馈网络和PWM脉冲调制器的传递函数；Vm为PWM调制器中锯齿波的幅值；R1和R2分别为系统反馈网络的分压电阻值。

将表2中的电路参数代入式(4)，经过化简可得：

(5) 表2 Sepic电路系统额定工作参数Tab.2 System rated parameters of Sepic circuit

根据式(5)画出Go(s)的伯德图，如图4所示。由图4知Go(s)的相角裕度偏小且在截止频率处斜率约为-40dB/dec，此时系统的超调量和调节时间较大，导致较差的动态性与稳定性。为满足Sepic闭环系统对稳定性的要求，应对系统校正以使其相角裕度在45°左右，而幅值裕度在10dB左右，截止频率处的幅频曲线斜率升高至-20dB/dec[9]。

图4 开环回路增益函数伯德图Fig.4 Bode diagram of open loop gain function

对图4采用PID补偿网络进行校正，而PID补

偿网络的传递函数Gc(s)为：

(6)

式中，r1、r2、c1和c2分别是PID补偿网络上的电阻和电容；ωz1为积分转折频率；ωz2为滞后环节的转折频率；K为传递函数Gc(s)的增益。

由于系统的开关频率fs=50kHz(ωs=2πfs)，所以补偿后系统幅频曲线的截止频率ωp≈ωs/10=3.14×104rad/s，此频率下的相位裕量约为-40°，故而Gc(s)于ωp处的相位补偿裕量θ可设成80°，令积分转折频率ωz1=100rad/s，由式(7)得到滞后环节的转折频率ωz2=3.39×103rad/s。

(7)

根据式(5)和式(6)得校正后系统的闭环传递函数：

(8)

代入表2中的电路参数并化简得到式(9)，再由式(9)得到Gc(s)Go(s)/K的伯德图，如图5中虚线所示。根据图5中虚线可以测得Gc(s)Go(s)/K的幅频增益在ωp处的值为-52dB，因此需要对系统添加增益，使系统的幅频特性曲线穿越0dB线时，并恰好落在ωp处。

(10)

要使系统的幅频特性曲线在ωp处穿越0dB线，则应该使系统的幅频增益20lgK为52dB，所以根据式(10)得K=398，并由式(6)得PID的参数Kp=4.098，Ki=398，Kd=0.001175。把K值代入式(8)，得到校正后Gc(s)Go(s)的伯德图，如图5中实线所示。

图5 闭环网络传递函数的伯德图Fig.5 Bode diagram of closed-loop transfer function network

由图5中实线知校正后系统的相角裕度r=44.3°，截止频率ωc=3.14×104rad/s，幅值裕度A(w)=3.82dB，符合控制系统的静、动态特性要求。

3.2 Boost电路

采用与Sepic电路相同的PID校正方法，根据表3中电路系统额定工作参数得到Boost电路的PID补偿网络的参数Kp=9.797，Ki=944，Kd=0.003567。

表3 Boost电路系统额定工作参数Tab.3 System rated parameters of Boost circuit

4 仿真和实验

4.1 Sepic电路

在MATLAB的Simulink中搭建Sepic电路闭环仿真模型[12]，其中设置仿真时间为0.4s。在0.2s时输入电压由12V突变至24V，仿真得到三种控制方式对Sepic电路输出电压的控制波形，如图6所示。

图6(a)为PID控制的闭环输入和输出电压仿真波形，其参数为Kp=4.098，Ki=398，Kd=0.001175。

图6(b)为模糊PID控制的闭环输入和输出电压仿真波形，其中Ke=3，Kec=8，Kup=2，Kui=1，Kud=0.1。

图6(c)为变论域模糊自适应PID控制的闭环输入和输出电压仿真波形，其中误差和误差变化率的输入伸缩因子分别为αe(x)、αec(x)：

(11)

(12)

模糊输出修正量的输出伸缩因子：

(13)

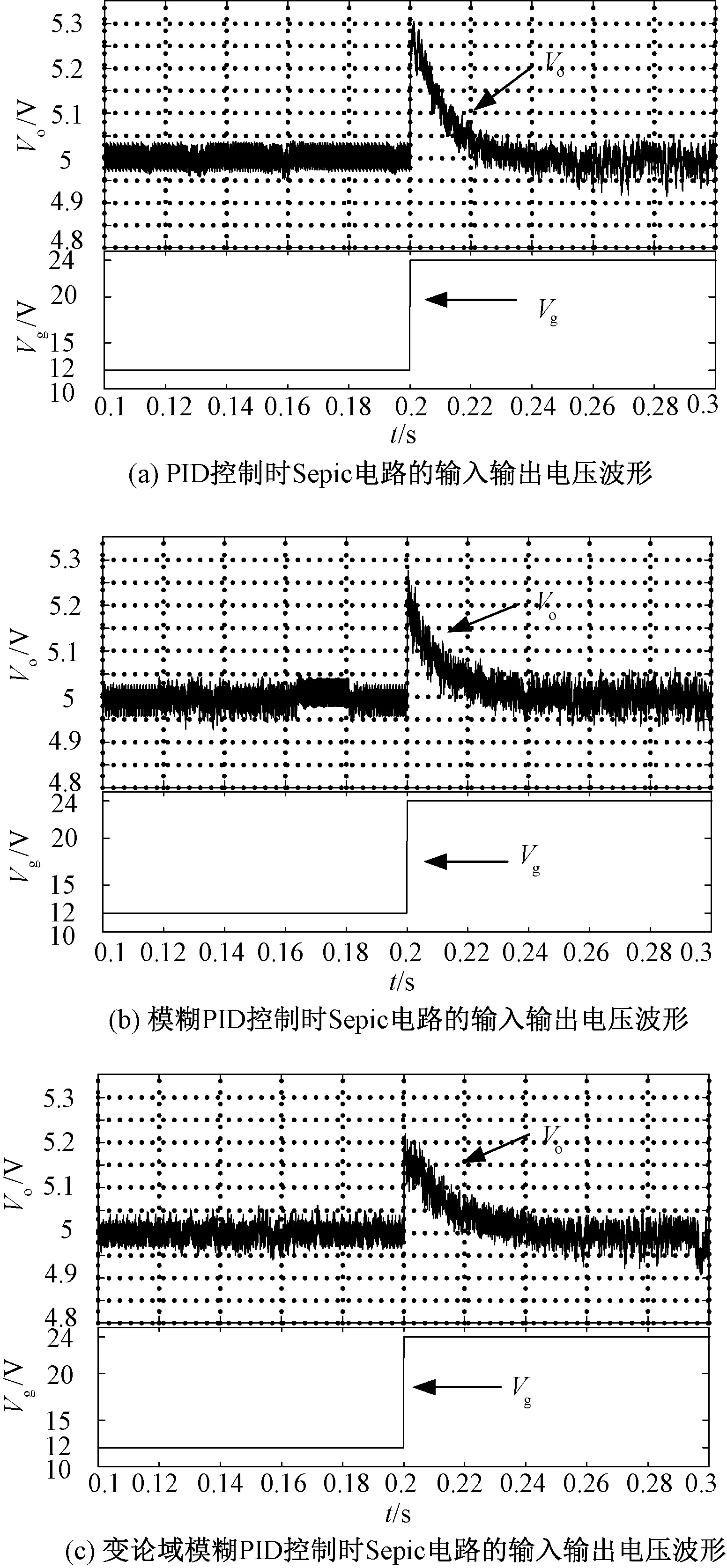
图6 Sepic电路仿真波形Fig.6 Simulation waveforms of Sepic circuit

通过对比图6(a)、图6(b)和图6(c)可知，变论域模糊PID控制与模糊PID控制和PID控制相比，其抗扰能力更强，动态性能更高。

为进一步确定所持理论的正确性，在实验室搭建了Sepic试验样机，采用STM32作为主控芯片，Sepic电路的输入输出电压实验结果如图7所示。为了使实验与仿真保持一致性，实验样机中的电路参数如表2所示。样机由Sepic主电路拓扑、5532采样保持电路、STM32单片机和IR2101驱动电路构成。电路额定工作时，输入电压为12V，输出电压为5V，电路工作频率为50kHz。

图7 Sepic电路实验波形Fig.7 Experimental waveforms of Sepic circuit

由图7知，变论域模糊PID控制对Sepic电路的闭环控制性能优于模糊PID控制和PID控制。在输入电压从12V突变到24V后，三种控制方法都能使输出快速地稳定在5V，但变论域模糊PID控制的动态性能(240ms)远优于PID控制(330ms)和模糊PID(295ms)。

4.2 Boost电路

在MATLAB的Simulink中搭建Boost电路闭环模型，设置仿真时间为0.4s，当输入电压从12V突变到18V时，仿真得到三种控制方式对Boost电路输出电压的控制波形，如图8所示。

图8(a)为PID控制的闭环输入和输出电压仿真波形，其参数为Kp=9.797，Ki=944，Kd=0.003567，仿真和实验使用位置式PID控制。

图8(b)为模糊PID控制的闭环输入和输出电压仿真波形，其中Ke=3，Kec=8，Kup=2，Kui=1，Kud=0.1。

图8(c)为变论域模糊PID控制的闭环输入和输出电压仿真波形，其中误差和误差变化率的输入伸缩因子为式(11)和式(12)，模糊输出修正量的输出伸缩因子为式(13)。

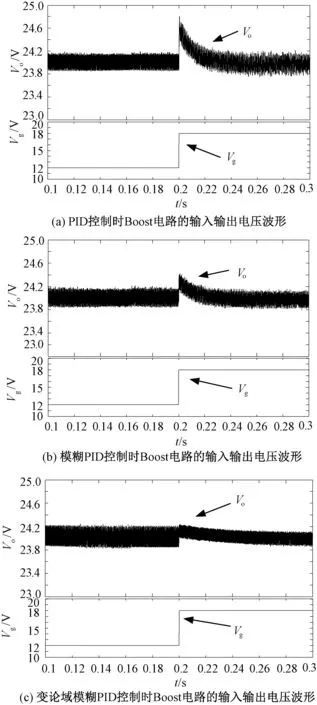
图8 Boost电路仿真波形Fig.8 Simulation waveforms of Boost circuit

为进一步确定所持理论的正确性，在实验室搭建了Boost试验样机，采用STM32作为主控芯片，Boost电路的输入输出电压实验结果如图9所示。为了使实验与仿真保持一致性，实验样机中的电路参数如表3所示。样机由Boost主电路拓扑、5532采样保持电路、STM32单片机和IR2101驱动电路构成。电路额定工作时，输入电压为12V，输出电压为24V，电路工作频率为50kHz。

图9 Boost电路实验波形Fig.9 Experimental waveforms of Boost circuit

对比图9(a)、图9(b)和图9(c)可知，实验结果验证了本文所提方法的有效性，变论域模糊PID控制在Boost电路中的闭环控制上性能优于另外两种控制方式，其抑制扰动能力更强，动态响应更快。在输入电压从12V突变到18V后，三种控制方法都能快速使输出稳定在24V，但是变论域模糊PID控制的动态性能(230ms)远优于PID控制(360ms)和模糊PID控制(305ms)。Sepic电路试验样机如图10(a)所示，Boost电路试验样机如图10(b)所示。

图10 试验样机Fig.10 Experimental prototype

5 结论

变论域模糊PID控制通过在模糊PID控制的模糊部分引入模糊论域伸缩因子，实现模糊论域随输入的变化而变化，既充分利用了控制系统的模糊规则，又提高了控制器的自适应能力，并使系统具有更高的控制精度、更快的反应速度和更强的抗干扰能力。根据文中的仿真和实验，可以得到如下结论：

(1)变论域模糊PID控制对Sepic变换器和Boost变换器的闭环控制，其控制效果与模糊PID控制和PID控制相比，控制系统动态响应快，电源输入发生突变时其自适应能力和抗干扰能力明显更强。

(2)相比于模糊PID控制和PID控制，变论域模糊PID控制更适合于开关电源的闭环系统的控制，如非线性非最小相位系统的DC-DC变换器。

[1] 甘家梁，王光伟，徐翠琴，等(Gan Jialiang，Wang Guangwei，Xu Cuiqin，et al.).模糊PID控制DC-DC转换器设计与仿真(Design and simulation of fuzzy PID control for DC-DC converter)[J].计算机仿真(Computer Simulation)，2014,31(10):386-418.

[2] H Elliott．Direct adaptive pole placement with application to non-minimum phase systems[J]．IEEE Transactions on Automatic Control，1982，27(3): 720-722.

[3] 皇金峰，刘树林(Huang Jinfeng，Liu Shulin). Boost变换器的参数选择与非最小相位分析(Parameter selection and analysis of non-minimum phase for Boost converter)[J].电机与控制学报(Electric Machines and Control),2014,18(7):51-59.

[4] 杨晓峰，吴敬兵(Yang Xiaofeng，Wu Jingbing).一种改进的非线性神经元PID控制方法在高压SVC中的应用(Improved non-linear neuron PID control method for application of high-voltage SVC)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2013，32(2):107-120.

[5] 李萍(Li Ping).模糊自整定PID控制器的设计和仿真(The design and simulation of fuzzy self-tuning PID controller)[J].仪器与仪表学报(Chinese Journal of Scientific Instrument)，2004，25(4)：264-267．

[6] 刘胜，刘江华(Liu Sheng，Liu Jianghua).变论域模糊PI在全范围调速系统中的应用设计(Application design for full range speed control system using variable universe fuzzy PI control)[J].电气传动(Electric Drive)，2015，45(12):50-54.

[7] 李红伟(Li Hongwei).变论域模糊控制的无刷直流电机控制系统(Brushless DC motor control system based on variable universe fuzzy control)[J].控制工程(Control Engineering of China)，2010，17(5)：599-602.

[8] 李洪兴(Li Hongxing).变论域自适应模糊控制器(Variable universe adaptive fuzzy controller)[J].中国科学E辑(Science in China(E)),1999,29(1)：32-42．

[9] 崔家瑞，李擎，张波，等(Cui Jiarui，Li Qing, Zhang Bo，et al.).永磁同步电机变论域自适应模糊PID控制(Permanent magnet synchronous motor of variable universe adaptive fuzzy PID control)[J].中国电机工程学报(Proceedings of the CSEE)，2013,33(S1)：190-194.

[10] 古超(Gu Chao).基于变论域模糊控制的温控器的研究(Research on temperture controller based on variable universe fuzzy control)[D].哈尔滨：哈尔滨工业大学(Harbin：Harbin Institute of Technology)，2008.

[11] 李洪兴(Li Hongxing).非线性系统的变论域稳定自适应模糊控制(Variable universe stable adaptive fuzzy control of non-linear system)[J].中国科学E辑(Science in China(E))，2002，32(2)：211-223．

[12] 杨玉岗，甘汶桦(Yang Yugang，Gan Wenhua).DC-DC Boost变换器控制算法的研究(Research on control algorithm of DC-DC Boost converters)[J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(3)：72-75.

Research on performance of variable universe fuzzy PID control in improving nonlinear non-minimum phase system for DC-DC converter

YANG Chao, YUAN Hong, YU Dai-ling, DING Xin-ping

(School of Automation Engineering, Qingdao University of Technology, Qingdao 266520, China)

Apart from Buck circuit, the dynamic model of traditional DC-DC circuit is a non-linear and non-minimum phase system, which is greatly influenced by the dynamic characteristics of the circuit parameters and dynamic model. PID control must be based on accurate mathematical model, but the non-linearity of DC-DC converter determines that the PID regulator is difficult to achieve better results. Fuzzy PID control does not require a precise mathematical model, and eliminates the static error of Fuzzy control. However, the adaptive capacity of the control is low, and when the input amount changes heavily, the control precision is deteriorated. Using the stretching factor, variable universe fuzzy PID control improves the adaptive capacity of system and increases the utilization rate of the fuzzy rules, improving the control accuracy. This paper studies the performance of variable universe fuzzy PID control in the non-linear and non-minimum phase system of DC-DC converter closed-loop control. Taking sepic circuit and Boost circuit as examples, these circuits belong to the typical non-linear and non-minimum phase system of DC-DC converter, and simulation and experiment have been carried out, which show that the proposed control method has better control performance than two other control methods.

variable universe fuzzy PID control; non-minimum phase system; DC-DC converter; stretching factor

2016-03-23

国家自然科学基金项目(51477079)、 山东省自然科学基金项目(ZR2013EEM020)、 中国博士后科学基金项目(2013M531598)。

杨 超(1990-)， 男， 安徽籍， 硕士研究生， 研究方向为新能源发电系统； 苑 红(1990-)， 男， 山东籍， 硕士研究生， 研究方向为新能源发电系统。

TM762

A

1003-3076(2017)01-0030-08