手脑并用“话”路径
周豪敏


[摘 要] 探索动点路径的形状和计算路径的长是学生解决的难点,要求学生具有较高的空间想象能力和分析问题的能力. 本文旨在通过学生自主的“手脑”活动,初步探究解决动点路径问题的基本方法.
[关键词] 动点;路径;解析法;数学活动经验
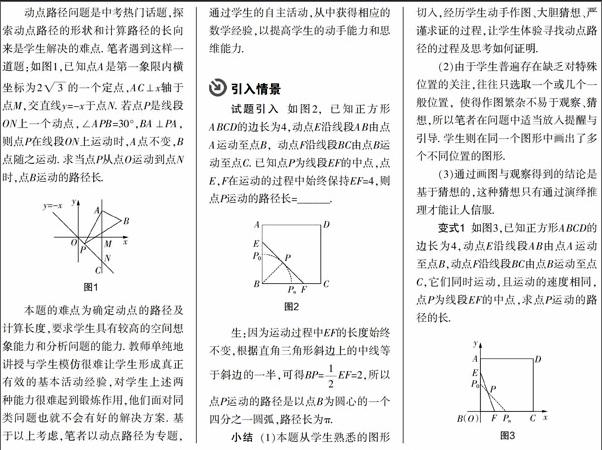
本题的难点为确定动点的路径及计算长度,要求学生具有较高的空间想象能力和分析问题的能力. 教师单纯地讲授与学生模仿很难让学生形成真正有效的基本活动经验,对学生上述两种能力很难起到锻炼作用,他们面对同类问题也就不会有好的解决方案. 基于以上考虑,笔者以动点路径为专题,通过学生的自主活动,从中获得相应的数学经验,以提高学生的动手能力和思维能力.
引入情景
试题引入 如图2,已知正方形ABCD的边长为4,动点E沿线段AB由点A运动至点B,动点F沿线段BC由點B运动至点C. 已知点P为线段EF的中点,点E,F在运动的过程中始终保持EF=4,则点P运动的路径长=______.
小结 (1)本题从学生熟悉的图形切入,经历学生动手作图、大胆猜想、严谨求证的过程,让学生体验寻找动点路径的过程及思考如何证明.
(2)由于学生普遍存在缺乏对特殊位置的关注,往往只选取一个或几个一般位置,使得作图繁杂不易于观察、猜想,所以笔者在问题中适当放入提醒与引导. 学生则在同一个图形中画出了多个不同位置的图形.
(3)通过画图与观察得到的结论是基于猜想的,这种猜想只有通过演绎推理才能让人信服.
变式1 如图3,已知正方形ABCD的边长为4,动点E沿线段AB由点A运动至点B,动点F沿线段BC由点B运动至点C,它们同时运动,且运动的速度相同,点P为线段EF的中点,求点P运动的路径的长.
小结 (1)在试题引入的经验基础上,笔者趁热打铁,通过改变条件,让学生自主探索,经历一次路径形状和计算的过程. 一方面巩固探究的方法,另一方面也给学生呈现一种不同的路径形状,激发学生的学习热情.
(2)通过建立合适的平面直角坐标系,借助一次函数知识,利用解析法巧妙地证明三点共线问题,体现了数形结合的数学思想,开阔了学生的视野.
(3)适时总结有助于学生巩固已有的活动经验.
变式2 在变式1的条件下,如图4,连接AF,ED交于点Q,求点E,F在运动过程中点Q运动的路径长.
生:运动过程中始终有∠AQD=90°,所以我认为点Q的运动路径为圆弧,圆心为AD的中点,半径为2,路径长为π.
变式3 如图5,等边三角形ABC的边长为4,在AB,BC边上各取一点E,F,连接AF,CE交于点P,若AE=BF,当点E从点A运动到点B时,点P经过的路径是什么形状?
生:同变式2,有△ABF≌△CAE. 在运动的过程中始终有∠APC=120°,所以我认为此时AC不是直径而是一条弦,圆心在三角形外面,点P经过的路径是一条弧线,是以AC为弦,∠APC=120°的圆中的弧AC.
师:若AE=CF,当点E从点A运动到点B时,点P经过的路径是什么形状?
生:因为AE=CF,所以易得△AEC≌△CFA,所以点P始终在AC边的高上.
小结 (1)经历试题引入及变式1,学生已有部分经验和积累,能对条件进行分析,从而给出相应的猜想和证明. 在变式2的探究过程中,有一部分学生通过分析获得结论,说明空间想象能力和分析问题的能力有一定的提升.
(2)变式2、变式3中条件的改变获得不同的路径形状,能让学生体验到数学的变化和魅力.
解决问题,巩固升华
下面我们解决开篇所提的问题(图1).
师:课后小作业为思考本题是否可用解析法证明三点共线.
课后思考及延伸
思路 运用解析法:点在直线上,则点的坐标满足所在直线的函数解析式.
常规想法 求出直线B0Bn的函数解析式,继而求得交点坐标B,将点B的坐标代入直线B0Bn的函数解析式的两边,验证相等.
困惑 运算量大.
调整后的想法一 如图7,利用△ADP∽△BEA,可获得点B的坐标,观察横坐标和纵坐标之间的联系,发现点B的纵坐标减去横坐标为一定值,即yB-xB为定值,继而可获得点B在直线上运动的结论.
回顾和总结
教师需要认识到学生在掌握“双基”的同时,还要增强数学基本活动经验. 比如动手作图、大胆猜想、严谨求证. 教师在平时的数学教学过程中,要有意识地通过一类数学问题及其变式,加强学生的数学基本活动经验,提高其分析问题和解决问题的能力.
必要的反思有助于增强学生的数学活动经验. 作为教师,应在实际教学过程中让学生多经历相应的反思活动. 例如对活动过程的反思;对某一解法的总结和比较;课后的思考和延伸.
教师要善于利用基本图形,能进行适当变式. 学生面对教师的一讲到底,被动地接受,做大量的类似题,效率往往大打折扣. 如能经常进行变式和拓展,就能调动学生学习的积极性、探索的自主性,从而提高上课效率. 正是老教师所说:做题不在于多,而在于精!

