一种新的区间二型模糊集排序方法

周 林 涛， 李 洪 兴

( 大连理工大学 控制科学与工程学院, 辽宁 大连 116024 )

一种新的区间二型模糊集排序方法

周 林 涛， 李 洪 兴*

( 大连理工大学 控制科学与工程学院, 辽宁 大连 116024 )

区间二型模糊集排序是模糊决策领域中的一个重要内容，然而文献中排序方法在某些情形下无法区分区间二型模糊集的排序顺序．针对这一问题，给出了一种新的基于模糊集内心的排序方法，依据排序值的大小来确定区间二型模糊集的排序顺序．与已有排序方法相比较，所给方法能够有效区分区间二型模糊集的排序顺序．

区间二型模糊集；模糊集内心；排序方法

0 引 言

作为一型模糊集的扩展[1]，二型模糊集的隶属度为区间[0,1]上的一型模糊集．二型模糊集隶属度上多出的一维使得它在表示模糊性时，具有了比一型模糊集更多的灵活性[2]．因此，有关二型模糊集的研究越来越受到人们的重视[3-4]．二型模糊集已经被大量地应用到人工智能、控制工程、优化与决策等各个领域[5-7]．

然而，计算的复杂性制约了二型模糊集在更多实际问题中的应用．为了解决这个瓶颈问题，很多研究者对涉及二型模糊集的规则约简、表示方法等问题进行了大量的研究[3-4,8-9]．Zhou等[8]提出了一种构造简约二型模糊系统的规则约简方法，并给出了4条衡量二型模糊规则贡献大小的评价指标．随后，Zhou等[9]还给出了一个新的二型模糊有序加权平均算子，并用该算子来聚合基于二型模糊集的决策变量及偏好信息．Mendel等[3]则提出了区间二型模糊集的概念，它将二型模糊集的隶属函数定义为区间值函数，简化了二型模糊集的表示，从而使计算变得简单．因此，区间二型模糊集在理论研究和计算方面具有了其他高阶模糊集所不可比拟的优势[4]．在模糊决策等应用问题中，经常会用到区间二型模糊集的排序，因而产生了大量的区间二型模糊集排序方法[10-19]，如 Chen和Lee提出了基于可能度的梯形区间二型模糊集排序方法[10]，并给出了梯形区间二型模糊集的运算规则．Hu等[14]则对Chen 和 Lee的方法进行改进，给出了基于可能度的梯形区间二型模糊集排序新方法．Wang等将期望值法解模糊化方法推广到区间二型模糊集，给出了基于期望值的区间二型模糊集排序方法[15]．Ghorabaee等将三角模糊数重心法解模糊化方法推广到区间二型模糊集，给出了基于模糊集重心的区间二型模糊集排序方法[17]．然而，在某些情况下，上述排序方法无法区分区间二型模糊集的排序顺序．因此，对区间二型模糊集的排序方法进行研究仍然有必要．

本文首先重新定义梯形区间二型模糊集的运算规则，克服Chen和Lee所给定义[10]中存在的不足．然后，给出一种基于模糊集内心的梯形区间二型模糊集排序方法．最后，将本文方法同文献中方法进行比较，以验证本文方法的实用性．

1 基本概念

Mendel等[3]最先给出区间二型模糊集的概念，随后Chen和 Lee在应用中给出了区间二型模糊集的运算定义[10]．

其中Jx⊆[0,1]．

其中Jx⊆[0,1]．

(1)

图1 梯形区间二型模糊集

在区间二型模糊集的排序方法中,常利用表示上隶属函数和下隶属函数的一型模糊集来确定其排序顺序．如在文献[10]中,Chen 和 Lee将基于可能度的一型模糊集排序方法推广到区间二型模糊集, 给出了基于可能度的区间二型模糊集排序方法，依据区间二型模糊集的排序值大小来确定排序顺序．

其中

2 区间二型模糊集的运算

Chen和Lee给出了区间二型模糊集的运算规则，然而该运算规则忽略了区间顶点隶属度的作用，并且隶属函数的定义域取值必须为正值．结合直觉模糊集定义[20-22]，本文重新定义梯形区间二型模糊集的运算，以改进原有定义中存在的不足．

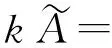
其中k∈R+．

显然，相比Chen 和 Lee在文献[10]中所给的运算规则，本文在定义梯形区间二型模糊集的运算时，考虑了隶属值Hi(AT)，i∈{1,2}，T∈{U,L}对运算的影响，并且克服了隶属函数在定义域内取值必须非负的不足．

3 基于模糊集内心的排序方法

三角形内心具有唯一性，且到三角形三边距离相等，基于此特性，Rouhparvar[23]给出了基于三角模糊数内心的解模糊化方法，并验证了用解模糊化值来确定模糊集排序顺序的合理性和有效性．结合三角模糊数内心法解模糊化方法，本文给出基于模糊集内心的梯形区间二型模糊集排序方法．

(2)

(3)

(4)

图2 三角模糊集

图3 梯形模糊集

(5)

实验组机械通气时间(7.47±3.34)天和呼吸机相关性肺炎发生率(4.00%)均显著低于对照组(12.31±4.47)天和(22.00%),P<0.01,差异具有统计学意义。结果见表1。

(6)

(7)

在排序区间二型模糊集时，依据排序值的大小来确定其排序顺序．当排序值相等时，认为两个区间二型模糊集等价．

4 数值分析

Bortolan和Degani在文献[24]中给出了13个具有代表性的模糊集，这13个模糊集常用来检验各种排序方法的效果，如表1所示．

表1 13个模糊集

按照文献和本文所给的排序方法计算表1中的13个模糊集，所得计算结果如表2所示．

表2 不同方法的排序结果

4.1 计算结果比较

(1)根据表2中Set1的比较结果可知，文献[10,17-18]和本文方法的排序结果一致；

(2)根据表2中Set2～Set6、Set8、Set9和Set11的比较结果可以看出，文献[10,13-14,16-18]和本文方法的排序结果一致；

(3)根据表2中Set7的比较结果可以看出，只有本文和文献[16]中的方法能区分两个模糊集的排序顺序；

(4)根据表2中Set10的比较结果可知，文献[10,13,16-18]和本文方法的排序结果一致；

(5)根据表2中Set12的比较结果可知，文献[10,14,16]和本文方法的排序结果一致，文献[13,17-18]不能区分两个模糊集的大小；

(6)根据表2中Set13的比较结果可知，文献[13,17-18]和本文方法的排序结果一致．

4.2 排序方法比较

将本文方法与文献[10-18]中的排序方法相比较可以发现：

(1)除了文献[15]以外，只有本文方法在运算中考虑了模糊集的区间顶点隶属度，从而保留了更多的计算信息．

(2)本文方法不仅能够区分模糊集的大小，而且比大多数排序方法要简便．

在算法的复杂性对比中，常以空间复杂度和时间复杂度来衡量一种计算方法的优劣．假设以时间复杂度作为衡量标准，要确定一组n个模糊集的排序顺序，用计算中出现乘法运算的次数来表示算法复杂度，对比几种排序方法的算法复杂度：

①在文献[10]中，计算一个模糊集的排序值需要进行2(n-1)次乘法运算，共有n个模糊集，确定全部排序时运行乘法的次数T′n=2n(n-1)+4n+1，因此时间复杂度为O(n2)；

②在文献[14]中，确定一个模糊集的排序值需要计算n次乘法，排序n个模糊集需要运行的乘法次数T″n=n2，因此时间复杂度为O(n2)；

③在文献[17]中，计算n个模糊集的排序值共需要进行的乘法次数T‴n=12n2，因此时间复杂度也为O(n2)；

④在文献[18]中，采用概率分布函数法计算模糊集的排序值，需要进行积分运算；

⑤在文献[13,16]和本文方法中，计算一个区间二型模糊集的符号距离、自适应二维优势度以及内心时，需要进行K次乘法运算(K为常数)，共有n个模糊集排序，共需要进行Kn次乘法运算，因此时间复杂度均为O(n)．

可见本文方法的时间复杂度要比大多数排序方法的时间复杂度低，计算更简便．

(3)在某些情形下，其他一些排序方法失效，不能区分两个模糊集的排序顺序，而本文方法却仍然能够区分，如Set7和Set12的排序．

5 结 语

本文定义了梯形区间二型模糊集的运算，并基于模糊集内心给出了一种新的梯形区间二型模糊集排序方法．文中在定义梯形区间二型模糊集运算规则时，考虑了区间顶点隶属度对计算的影响，保留了更多的模糊性，减少了因计算而造成的信息丢失．结合三角模糊数内心法解模糊化方法，给出了基于模糊集内心的梯形区间二型模糊集排序方法．以经典的13个模糊集为例，将本文方法与其他排序方法做对比分析，结果表明，文中所给的区间二型模糊集排序方法较大多数排序方法简便、有效，而且能区分其他排序方法不能区分的区间二型模糊集．对区间二型模糊集排序方法进行研究，促进了其在实际问题中的应用，一个准确、有效的排序方法在实际应用中是必要的．

[1] ZADEH L A. The concept of a linguistic variable and its application to approximate reasoning [J]. Information Sciences, 1975, 8:199-249.

[2] WU Dongrui, MENDEL J M. Aggregation using the linguistic weighted average and interval type-2 fuzzy sets [J]. IEEE Transactions on Fuzzy Systems, 2007, 15(6):1145-1161.

[3] MENDEL J M, JOHN R I, LIU Feilong. Interval type-2 fuzzy logic systems made simple [J]. IEEE Transactions on Fuzzy Systems, 2006, 14(6):808-821.

[4] MENDEL J M. General type-2 fuzzy logic systems made simple:A tutorial [J]. IEEE Transactions on Fuzzy Systems, 2014, 22(5):1162-1182.

[5] GANJEFAR S, SOLGI Y. A Lyapunov stable type-2 fuzzy wavelet network controller design for a bilateral teleoperation system [J]. Information Sciences, 2015, 311:1-17.

[6] ZHOU Shangming, CHICLANA F, JOHN R I,etal. Type-1 OWA operators for aggregating uncertain information with uncertain weights induced by type-2 linguistic quantifiers [J]. Fuzzy Sets and Systems, 2008, 159(24):3281-3296.

[7] CHICLANA F, ZHOU Shangming. Type-reduction of general type-2 fuzzy sets:The type-1 OWA approach [J]. International Journal of Intelligent Systems, 2013, 28(5):505-522.

[8] ZHOU Shangming, GARIBALDI J M, JOHN R I,etal. On constructing parsimonious type-2 fuzzy logic systems via influential rule selection [J]. IEEE Transactions on Fuzzy Systems, 2009, 17(3):654-667.

[9] ZHOU Shangming, JOHN R I, CHICLANA F,etal. On aggregating uncertain information by type-2 OWA operators for soft decision making [J]. International Journal of Intelligent Systems, 2010, 25(6):540-558.

[10] CHEN Shyiming, LEE Liwei. Fuzzy multiple attributes group decision-making based on the ranking values and the arithmetic operations of interval type-2 fuzzy sets [J]. Expert Systems with Applications, 2010, 37(1):824-833.

[11] CHEN Shyiming, LEE Liwei. Fuzzy multiple attributes group decision-making based on the interval type-2 TOPSIS method [J]. Expert Systems with Applications, 2010, 37(4):2790-2798.

[12] CHEN Shyiming, YANG Mingwey, LEE Liwei,etal. Fuzzy multiple attributes group decision-making based on ranking interval type-2 fuzzy sets [J]. Expert Systems with Applications, 2012, 39(5):5295-5308.

[13] CHEN Tingyu. A linear assignment method for multiple-criteria decision analysis with interval type-2 fuzzy sets [J]. Applied Soft Computing Journal, 2013, 13(5):2735-2748.

[14] HU Junhua, ZHANG Yan, CHEN Xiaohong,etal. Multi-criteria decision making method based on possibility degree of interval type-2 fuzzy number [J]. Knowledge-Based Systems, 2013, 43:21-29.

[15] WANG Jianqiang, YU Sumin, WANG Jing,etal. An interval type-2 fuzzy number based approach for multi-criteria group decision-making problems [J]. International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, 2015, 23(4):565-588.

[16] CHANG Jingrong, CHENG Chinghsue, KUO Chenyi. Conceptual procedure for ranking fuzzy numbers based on adaptive two-dimensions dominance [J]. Soft Computing, 2006, 10(2):94-103.

[17] GHORABAEE M K, AMIRI M, SADAGHIANI J S,etal. Multiple criteria group decision-making for supplier selection based on COPRAS method with interval type-2 fuzzy sets [J]. The International Journal of Advanced Manufacturing Technology, 2014, 75(5):1115-1130.

[18] LEE E S, LI R J. Comparison of fuzzy numbers based on the probability measure of fuzzy events [J]. Computers & Mathematics with Applications, 1988, 15(10):887-896.

[19] 李荣钧. 模糊决策的基础——模糊集比较与排序[J]. 控制与决策, 2003, 18(2):221-224.

LI Rongjun. Basis of fuzzy decision — Comparison and ranking of fuzzy sets [J]. Control and Decision, 2003, 18(2):221-224. (in Chinese)

[20] WANG Jianqiang, NIE Rongrong, ZHANG Hongyu,etal. New operators on triangular intuitionistic fuzzy numbers and their applications in system fault analysis [J]. Information Sciences, 2013, 251:79-95.

[21] WANG Jianqiang, NIE Rongrong, ZHANG Hongyu,etal. Intuitionistic fuzzy multi-criteria decision-making method based on evidential reasoning [J]. Applied Soft Computing Journal, 2013, 13(4):1823-1831.

[22] 张英俊,马培军,苏小红,等. 属性权重不确定条件下的区间直觉模糊多属性决策[J]. 自动化学报, 2012, 38(2):220-228.

ZHANG Yingjun, MA Peijun, SU Xiaohong,etal. Multi-attribute decision making with uncertain attribute weight information in the framework of interval-valued intuitionistic fuzzy set [J]. Acta Automatica Sinica, 2012, 38(2):220-228. (in Chinese)

[23] ROUHPARVAR H. A new definition for defuzzification of generalized fuzzy numbers and its application [J]. Applied Soft Computing Journal, 2015, 30:577-584.

[24] BORTOLAN G, DEGANI R. A review of some methods for ranking fuzzy subsets [J]. Fuzzy Sets and Systems, 1985, 15(1):1-19.

A new ranking method of interval type-2 fuzzy sets

ZHOU Lintao, LI Hongxing*

( School of Control Science and Engineering, Dalian University of Technology, Dalian 116024, China )

The ranking for interval type-2 fuzzy sets is one of the most critical issues in the fuzzy decision-making domain. The existing methods, however,cannot distinguish the ranking order of interval type-2 fuzzy sets in some cases.To solve this problem, a new ranking method of interval type-2 fuzzy sets is proposed based on incentre point of fuzzy sets; and then, a ranking order is defined according to the ranking value. Compared with the existing methods, the proposed method can effectively distinguish the ranking order of interval type-2 fuzzy sets.

interval type-2 fuzzy sets; incentre point of fuzzy sets; ranking method

2016-08-30；

2017-01-10．

国家自然科学基金资助项目(61374118).

周林涛(1981-)，男，博士生，E-mail:zltao@foxmail.com；李洪兴*(1953-)，男，教授，E-mail:lihx@dlut.edu.cn.

1000-8608(2017)02-0195-07

O159

A

10.7511/dllgxb201702013