三角模糊数去模糊化对VIKOR妥协解的影响研究
糜万俊, 江文奇, 戴跃伟
(1.南京理工大学 自动化学院,江苏 南京 210094; 2.南京理工大学 经济管理学院,江苏,南京 210094)
0 引言
VIKOR法(VlseKriterijumska Optimizacija I Kompromisno Resenje)是一种重要的多准则决策方法[1],主要利用各个备选方案的评价值与理想方案的接近程度来排列方案的顺序,比理想点法具有更高的排序稳定性、可信度,在质量部件的改善[2]、装备器材供应商选择[3]、供应商选择[4,5]等等多个领域。
模糊VIKOR法是近年来的研究热点问题之一。文[6]提出了一种基于直觉模糊值的新评分函数和VIKOR方法,克服了现有评分函数、现有的准确度函数和现有的IFV排序方法的缺点。文[7]研究了含有犹豫区间型Pythagorean模型信息的多属性决策问题,提出了一种多阶段的VIKOR方法来解决多属性决策问题。文[8]针对属性值为Pythagorean 不确定语言变量, 属性权重和专家权重完全未知的群决策问题, 提出一种扩展VIKOR多属性群决策方法。文[9]提出相对VIKOR方法,旨在通过相对群体效用及相对个体遗憾确定一个相对最佳妥协解。文[10]针对属性值为直觉梯形模糊数,决策者间和属性间存在相互关联的多属性群决策问题,引入模糊测度和Choquet积分的概念,提出了基于诱导型广义直觉梯形模糊Choquet积分算子和多准则妥协优化解的直觉梯形模糊多属性群决策方法。文[11]将一种利用最小叉熵准则集成组合权重的思想运用到黑启动方案评估上,将原始属性评价矩阵转换为带有决策者主观偏好的判断矩阵,利用VIKOR法对方案间关系进行细致分析。文[12]针对群推荐系统中被推荐项目具有多粒度性、犹豫性、模糊性的特点, 提出多粒度犹豫模糊语言熵的概念及计算公式,将传统的多准则妥协解排序法VIKOR拓展到多粒度犹豫模糊领域。文[13]针对备选方案的属性值为三角直觉模糊数且权重为实数的多属性决策问题,研究了三角直觉模糊数型VIKOR方法。文[14]针对权重未知的模糊多属性大群体决策问题,提出基于Humming距离构建决策者权重优化模型,基于VIKOR框架,采用区间直觉模糊均衡交叉熵计算各方案、临界解与理想解的空间测度并实现方案排序。
在模糊VIKOR方法中,群体效用值、个体遗憾值和其合成值均需要进行模糊数的数学运算。在准则值和准则权重均为三角模糊数的多准则决策中,可能存在某些运算结果并不符合三角模糊数特征,进而需要进行去模糊化处理。论文将深入研究去模糊化的前提条件,不同的去模糊化方法获得的清晰数值比较,提出一种基于拓展的模糊VIKOR方法并加以应用。
1 三角模糊数去模糊化
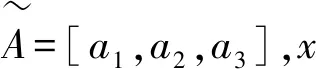
(1)
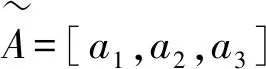

(2)
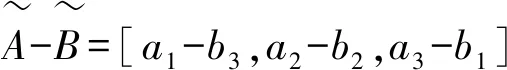
(3)

当a1或者b1至少一个大于零
(4)
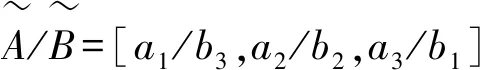
(5)
常数可以看成三个端点均相等的三角模糊数,采用定义2设定的规则计算即可。如果将三角模糊数转化为清晰数,则主要有如下几种去模糊化方法:
(6)
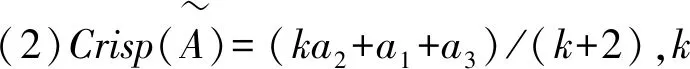
(7)
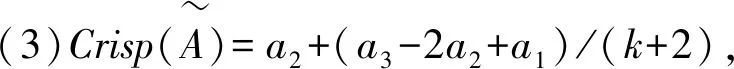
(8)
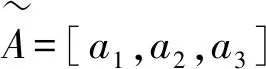
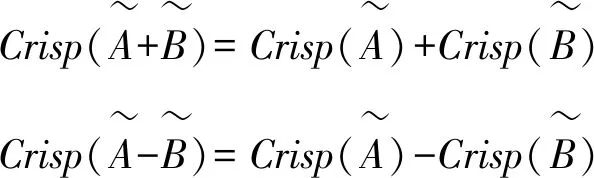
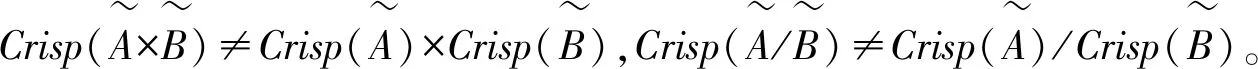
(2)如果采用公式(7)去模糊化(式(6)去模糊化值是式(7)的特例),则:
数学运算结果与上述相同。
(3)如果采用公式(8)进行去模糊化,则:
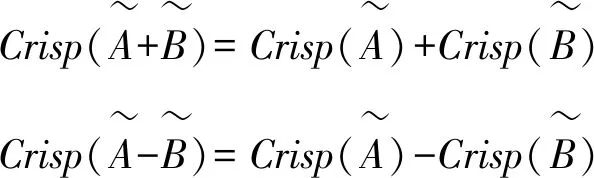
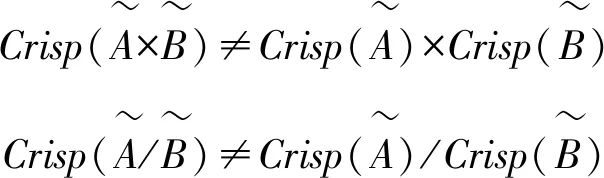
尽管采用式(7)和(8)得到的数学运算结果与式(6)相类似,但是参数k对最终的结果产生影响。随着k值的增加,三角模糊数中间值对去模糊化值影响将会越来越大。同时,在三种去模糊化方法下乘法和除法运算规则得到的合成去模糊化结果,均不等于两者分别去模糊化的合成值,说明在运算中不应该分别进行去模糊化。
2 VIKOR法中三角模糊数去模糊化必要性
VIKOR方法是一种对复杂系统进行多准则决策的折衷排序方法,折衷解是所有解中最为接近理想解的可行解,是属性间彼此让步的结果,也是理想点法改进的结果。
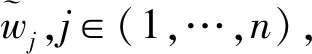
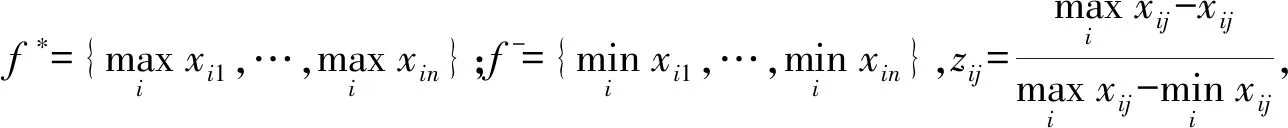
令v为大多数准则策略的决策机制系数,v>0.5表明根据大多数人的意见决策,v=0.5表明根据赞同情况决策,v<0.5表明根据拒绝情况进行决策。有:

不是一般性,假定依据Qi值得到排序第一和第二的方案分别为a1和a2[8]。
条件1可接受度优势。Q2-Q1≥1/(m-1),m为方案数目。
条件2决策过程中可以接受的稳定性,a1同样是Si或Ri中排序第一的方案。
如果条件1和2均满足,则a1为排序第一的方案。如果上述条件有1个不满足,有:如不满足条件2,则a1和a2均为折衷解;如果不满足条件1,则通过Q2-Q1<1/(m-1)得到最大的M,a1,…,aM,均贴近理想方案。
从VIKOR方法步骤来看,主要有以下环节可能需要进行去模糊化。
(1)zij值的计算。zij值的分母是准则cj下每个准则值的最大值与最小值的差值。尽管两者去模糊化之后的差值一定为正数,但依据减法运算规则,仍可能存在差值(三角模糊数)中存在负数的情形。例如:针对某个准则,其最大和最小的准则值分别为(0.5,0.8,0.9)和(0.4,0.6,0.7),则两者的差值为(-0.2,0.2,0.5)。如果直接采用式(5)的除法规则,会导致得到的三角数的右端点值小于左端点的值,不符合三角模糊数的本质特征(三个端点值逐步增加)。
(2)Qi值的计算。按照判断妥协解的条件1要求,需计算排序第一位和第二位方案Qi值的差值,故需要对每个模糊Qi值进行去模糊化,才能获得差值并判断是否满足条件1。
3 去模糊化对VIKOR妥协解的影响
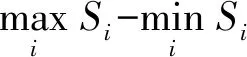
对zij值而言,如其分母(三角模糊数)的值均为正数,令:zij=(a,b,c)/(d,e,f)。
如果采用式(6)进行去模糊化,去模糊化的值分别为:
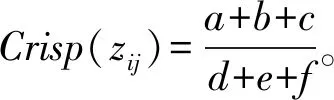
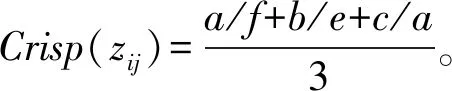
如果采用式(7)和式(8)进行去模糊化,上述两种情形下的计算结果均分别为:
采用三种去模糊化方法对两种情形下的zij值进行去模糊化的结果表明:
(1)在两种情形下,采用不同的去模糊化方法得到的结果是不同的。第二种和第三种方法更加注重三角模糊数中间值对去模糊化的值影响,随着k值的增加,影响越来越大。情形1下如果a,b,c且d,e,f接近,情形2下如果a/f,b/e,c/a接近,则采取三种方法得到的清晰数接近,可以采取任何一种方法去模糊化。
(2)针对同一种去模糊化方法,两种情形下得到的清晰数存在一定的差异,如果差异较大,则可能对群体效用值和个体遗憾值产生影响。即如果仅仅对部分准则下zij的分母去模糊化,则该准则下zij的值发生变化,进而造成合成值(群体效用值和个体遗憾值)发生变化,间接对Qi值产生影响,造成妥协解的改变。
于是,基于VIKOR方法的多准则决策过程可以描述为:
步骤1针对第三节的模糊多准则决策矩阵,由于量纲不同,需要进行无量纲化处理。
对权重归一化,有

步骤2确定正负理想方案。依据三角模糊数可能度公式,即:
(9)
分别比较各个准则下准则值之间的可能度,确定f*,f-。



步骤5按照第三节提供的Qi值计算公式计算Qi。如果计算Qi过程中遇见和zij值计算相同的情形,则按照步骤3 的方式进行计算。
步骤6基于第三节提出的两个条件和Qi值确定妥协解。
4 实例分析
某风险投资企业致力于寻求合适的设备风险投资项目,现有4个备选方案,考虑的准则主要有环境影响c1、预期收益c2、成长性c3、社会效益c4,第一个准则为成本型准则,其他均为效益型准则。决策矩阵分别见表1。

表1 多准则决策矩阵
步骤1对上述三个决策矩阵进行无量纲化处理,见表2。

表2 多准则决策矩阵无量纲化表
假定四个准则的权重分别为(0.2,0.3,0.4),(0.6,0.7,0.8),(0.3,0.4,0.5)和(0.4,0.5,0.6)。归一化值分为(0.087,0.158,0.267),(0.261,0.368,0.533),(0.130,0.211,0.333)和(0.174,0.263,0.400)。
步骤2按照可能度公式,选出正负理想解,分别为:
正理想解(0.738,0.951,1.000),(0.968,1.000,1.000),(0.768,1.000,1.000),(0.750,1.000,1.000)
负理想解(0.660,0.848,0.977),(0.894,-0.935,0.989),(0.549,0.691,1.000),(0.250,0.500,0.667)

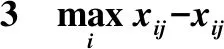
表表
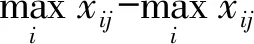

表4 zij值
采用式(6)对其进行去模糊化的值见表5。

表5 zij值的去模糊化结果

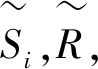
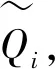

表6 VIKOR中
步骤6采用式(6)方式去模糊化,得到a3,a2均为妥协解。如果采取式(7)进行去模糊化,则从k=1开始,Q2-Q1值分别为0.128,0.38,0518,0.616等,逐步增加,此时妥协解为a2。如果采取式(8)的方法,则从k=2开始,Q2-Q1值分别为0.216,0.438,0.576,0.66等,值仍然逐步增加,妥协解为a2。
5 结论
VIKOR方法中的三角模糊数运算是核心,是获得群体效用值和个体遗憾值以及妥协解的必须环节。由于三角模糊数的合成运算并非满足运算规则,因此论文重点分析了三角模糊数去模糊化的前提条件和如何选择合适的去模糊化方法,并给出了一种拓展的VIKOR方法解决含有三角模糊数的多准则决策问题,案例验证了本文的分析结果。

