跳扩散条件下波动率风险溢价及影响因素研究——基于上证50 ETF期权市场的实证

王苏生， 胡明柱， 李梓龙

(哈尔滨工业大学(深圳) 经济管理学院，广东 深圳 518055)

0 引言

2015年2月9日，经证监会批准，上证50 ETF期权在上海证券交易所正式推出，标志着中国内地金融市场迈入多元投资新时期[1]，但同时也伴随着新的风险源及溢价，准确认识金融市场中的风险源对金融市场监管者、投资者及金融中介机构等是至关重要的。近些年来随着衍生品的发展，股权风险溢价等一阶矩风险源的研究已经不能满足金融市场的需求，人们对风险源的研究更为深入，开始关注波动率风险、相关性风险、偏度风险及峰度风险等高阶矩风险，以适应金融市场发展的需要，而波动率风险是高阶矩风险的代表之一，也是目前金融研究的热点(如：Chen等[2]、Della等[3]、Johnson等[4]、Londono等[5])。

波动率风险是市场风险的重要来源且是资产价格随机过程在风险中性概率测度和已实现概率测度之间转换的重要纽带，被认为是传统CAPM定价模型及期权定价模型等经典估值模型与实际市场定价产生偏误的重要原因之一；资产定价理论表明，只要市场中存在风险源，投资者必然寻求对应的风险溢价，但是传统的CAPM理论仅考虑系统性市场的收益风险，这样单一的考虑远远不能适应复杂多变的资本市场(陈蓉等[6])；多年来研究者们也纷纷寻找新的风险源及风险溢价，希望拓展传统CAPM理论以便更好地认识市场(王茵田等)[7]、Dew-Becker等[8])，因此，波动率风险溢价的研究是对CAPM理论的有益补充。另外，波动率风险溢价不仅在股票市场、外汇市场等中具有显著的预测作用(Della等[3]、Feunou B等[9]、Bollerslev T等[10])，而且具有风险预警作用(Bekaert等[11])。因此本文的研究对认识中国内地投资者波动风险态度、资产定价[12]、投资组合管理、风险管理及中国内地金融衍生品市场的建设与完善等具有重要的理论意义和实践意义。

传统的Black-Scholes模型假设股票价格服从几何布朗运动且波动率是常数，然而这些严格假设偏离了市场的实际情况，造成期权定价误差较大，后续学者们为了更好地拟合实际市场对Black-Scholes模型进行拓展，认识到波动率是随机的并非常数，而且具有时变特征；Heston[13]提出了随机波动率模型(Stochastic Volatility, SV)；由于突发的重大经济、政治、社会事件等会引起股指收益超常规的波动，虽然发生的概率较小，但是幅度却很大，因此，Bates[14]提出了收益跳跃随机波动率模型(Stochastic Volatility with Jumps in returns, SVJ)；接着，Duffie等[15]又提出了收益与波动均具有跳跃特征的随机波动率模型(Stochastic Volatility with Contemporaneous Jumps in returns and volatility, SVCJ)；由于波动率是随机的、是市场中存在的风险源，必然和相应的风险溢价对应，但由于随机波动率期权定价模型的公式复杂，模型往往没有解析解，想要从期权价格中剥离出波动率风险溢价是有一定难度的，这使得相关研究直到近些年才有所突破。Eraker等[16]使用马尔科夫蒙特卡洛方法(MCMC)对SVCJ模型的参数进行了估计；Broadie等[17]、Neumann等[18]使用MCMC等估计方法和期权市场的交易数据估计波动率风险溢价，但由于SVCJ模型复杂、涉及的期权合约众多，因此，计算时间冗长，存在明显的“计算负担(computational burden)”问题。Duan等[19]推导出SVJ模型与VIX指数之间的近似关系，使用最大似然估计法提取S&P500期权市场的波动率风险溢价，避开了“计算负担”问题；周林海等[20]、Xinyu等[21]和Papantonis等[22]等也使用这种近似关系估计溢价，尽管这种估计方法相对简单，但是VIX指数并不能反应具体期权合约的定价情况，近似推导必然产生误差问题，直接利用在学界也缺乏统一的认可度；因此，本文参照Broadie等[17]、Neumann等[18]等的做法直接使用期权市场的交易数据来估计波动率风险溢价。

目前中国内地学者针对波动率风险溢价的研究还较少，实证市场基本以中国香港、美国等为主，由于SVCJ模型结构复杂、计算难度大，因此主要聚焦相对简单的SV模型，如：陈蓉等[6]、吴鑫育等[23]等；但SV模型为资产收益和波动均非跳跃模型，因此或多或少忽略了市场的跳跃情况；而Brodie等[17]等研究表明SVCJ模型相较于SV、SVJ模型能够更好地吻合真实市场情形。Neumann等[18]研究也表明SVCJ模型在估计S&P500期权市场波动率风险溢价时相较于SV模型、SVCJ模型具有更好的拟合优度。另外，波动率风险溢价具有明显的时变性，为了更深入地研究波动率风险溢价的时变特征，学者们选取了多种合适的影响因子，研究波动率风险溢价随之变化的一般规律。陈蓉[6]使用恒生指数波动率、对数收益率作为影响因素来考察香港市场波动率风险溢价；郑振龙等[24]研究了中国台湾期权市场波动率、收益率、换手率对波动率风险溢价的影响。

中国内地金融衍生品市场起步较晚、期权推出的时间短，鲜有学者使用跳扩散随机波动率模型(SVCJ模型)从期权定价视角来研究上证50 ETF期权市场的波动率风险溢价。有别于大多数研究主要聚焦于美国等成熟金融市场，本文主要考察上证50 ETF期权市场波动率风险溢价的研究，相信对中国内地新兴期权市场的新特点的论述将是现有研究的重要补充，同时也为中国内地衍生品市场的进一步扩展提供借鉴。

通过实证研究表明SVCJ模型相较于SV模型及SVJ模型具有更好的市场拟合优度；本文较早的使用SVCJ模型、MCMC及傅里叶变换法等估计上证50 ETF期权市场的波动率风险溢价，对研究中国内地期权市场的波动率风险溢价方法是一个有效参考；本文使用傅里叶变换方法能有效提高溢价的估计效率，有效解决Neumann等[18]等提出的使用SVCJ模型提取波动率风险溢价时存在的“时间负担”(computational burden)问题；Bakshi G等[25]、Carr和Wu[26]、Duan等[19]、Tim Bollerslev等[27]及Bekaert等[11]等研究表明美国S&P500期权的波动率风险溢价为负，投资者是厌恶波动风险的；上证50ETF期权市场是否如美国S&P500期权市场一样为负的波动率风险溢价？波动率风险溢价蕴含的投资者的波动风险态度是厌恶型还是偏好型、如何对波动率风险溢价进行经济学解释等等，这都是学术界及实务界共同关注的重要问题，本文的研究是对现有研究的有益补充。

1 模型与理论分析

1.1 随机波动率模型

SVCJ模型的基本假设是资产的收益及波动均存在跳跃，模型在已实现概率测度(Physical measure，“P测度”)下的基本形式如式(1)和式(2)：

(1)

(2)

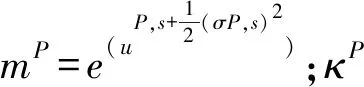
风险中性概率测度(Risk-neutral measure，“Q测度”)下方程的表达式为：

(3)

(4)

Q测度中各参数的定义与P测度中参数的定义类似，将P测度参数替换成Q测度下的参数即可。

SV模型及SVJ模型：SVJ模型和SV模型是SVCJ模型的特殊情况(Karl Larsson等[28])，当资产收益发生跳跃，而波动不发生跳跃，令uP,v=0，则为SVJ模型，当资产收益及波动均不发生跳跃，令uP,v=0及λP=0，则为SV模型，Q测度下类似；由于SV模型及SVJ模型为SVCJ模型的特殊形式，因此，接下来主要介绍SVCJ模型的参数估计方法。

1.2 参数估计方法

(1)P测度

本文使用MCMC估计方法和上证50 ETF时间序列数据估计P测度下的参数。MCMC估计方法是将马尔科夫过程引入蒙特卡洛模拟中，借以实现抽样分布随模拟进而改变的一种动态模拟方法，其广泛应用于经济金融参数估计领域。在应用MCMC方法来估计SVCJ模型中的参数时，需要使用Euler法对式(1)和(2)进行离散，离散后的SVCJ模型如：

(5)

(6)

其中，Yt+1=ln(St+1/St)，α=(rt+γt-λPmP)；εs,t+1和εv,t+1服从标准正态分布，且相关系数为ρP；Jt控制了跳跃的发生，当Jt=1时则发生跳跃，反之Jt=0时则不发生跳跃。待估计的变量如：

{Vt,Jt,ξt,ΘP=(κP,θP,σP,s,ρP,μP,s,σP,v,μP,v,λP)}

(7)

其中，ξt代表跳跃幅度，ΘP为待估参数向量，参照Neumann[18]中估计波动率风险溢价的做法，P测度下得到的瞬时波动率Vt将作为变量并结合期权交易数据估计Q测度下的变量。关于MCMC估计方法在此就不再赘述，详细介绍见Broadie等[17]、Neumann[18]等。

(2)Q测度

使用实际期权市场交易合约估计Q测度下SVCJ模型的参数，但在交易所每日交易的期权合约较多，长年累月的交易合约数量繁多；Neumann等[18]在使用Duffie[15]中的期权定价方法及(18)中的最小化方法模型来估计Q测度下SVCJ模型的参数时存在参数估计效率慢，即“时间负担”问题，为便于后续讨论，本文将这类方法称为“Duffie法”；为了提高参数的估计效率，本文根据Karl Larsson等[28]中的傅里叶变换期权定价方法及式(18)中的最小化方法来估计Q测度中SVCJ模型的参数，本文将这类方法称为“FFT法”。SVCJ模型特征函数的一般表达式：

q(z)=E[ezlog(St)],z∈C

(8)

(9)

(10)

logq(z)=A(T,z)+B(T,z)Vt+zlog(St)

(11)

(12)

A0(T,z)+λQA1(T,z)

(13)

(14)

(15)

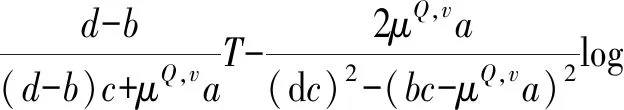
(16)

根据Karl Larsson等[28]的研究，只要得到Q测度下资产对数价格分布的特征函数，就可以利用傅里叶变换法求得欧式期权的定价公式，而应用傅里叶变换法可以提高参数的估计效率；根据上述原理，到期期限为T、执行价格为K的SVCJ模型的欧式看涨期权的定价表达式:

(17)

Broadie等[17]、Neumann等[18]等在使用SVCJ模型估计波动率风险溢价时对两概率测度下的参数做了适当限制，即λP=λQ；σP,s=σQ,s，σP,v=σQ,v；ρP=ρQ；κPθP=κQθQ，文本参照他们的做法设定这几个参数在两概率测度下的值相同，这样在Q测度下需要估计的参数包括：ΘQ={κQ、μQ,v、μQ,s}；使用期权交易数据及SVCJ模型的欧式期权定价公式，通过求解式(18)中的最小化问题来估计Q测度中模型的参数:

Pt(ΘQ/ΘP,K,τ,St,rt,Vt)]2

(18)

式(18)中，Pt(K,τ,St,rt,Vt)是上证50 ETF期权价格；K表示期权的执行价格；τ表示期权的剩余期限；Nt表示t时刻期权的数量；Pt(ΘQ/ΘP,K,τ,St,rt,Vt)通过随机波动模型计算得到的期权价格；rt表示无风险利率；在许多研究中，研究者们为了便于计算及程序设计，又由于无风险利率的变化不大，因此往往假设为定值，但本文为了更符合实际市场情况选用1年期上海银行间同业拆借利率(SHIBOR)数据作为无风险利率。

1.3 波动率风险溢价

Carr和Wu等[26]、Bollerslev等[10]和Londono等[5]等将波动率风险溢价(Volatility Risk Premium, VRP)定义为P测度下的已实现方差(Realized variance)与Q测度下的隐含方差(Implied risk-neutral variance)的期望之差，而方差在数值上为波动率的平方，因此，波动率风险溢价度量了标的资产的波动率在两种概率测度下的溢价水平，其表达形式为：

(19)

本文将波动率风险溢价定义为：

(20)

Lin Y N推导出SVCJ模型的方差期望在P测度与Q测度中的表达式：

(21)

(22)

由式(21)及(22)可知，波动率风险大致由扩散风险和跳跃风险两部分组成，它们分别反应了资产波动中的跳跃及扩散风险及资产价格跳跃而产生的波动风险；另外，T-t=τ，本文采用的是日频期权交易数据(τ=1)。

2 数据筛选与模型评价

2.1 数据筛选

本文选取上证50 ETF期权起始交易日2015.02.09至2018.06.30的日频交易数据。

数据来源：本文使用1年期上海银行间同业拆借利率(SHIBOR)数据作为无风险利率，数据来源于东方财富Choice金融终端；上证50 ETF期权交易的日频数据来源于上海证券交易所。

数据处理：在实证研究之前，根据以下原则对数据进行了筛选(陈蓉等[6])：

1)由于在临近交易日时，期权的价格波动较为剧烈，因此容易存在较大的定价误差，因此本文剔除剩余期限小于等于5日的期权数据；剩余期限太长，也受到随机利率等因素的影响，因此本文进一步剔除剩余期限大于60日的期权数据。

2)流动性较差的期权往往也存在较大的定价误差且容易受流动性风险影响，因此剔除每日交易量少于500手的期权数据。

3)剔除隐含波动率不存在或者为0的看涨看跌期权数据。

筛选后共有10900个期权合约；使用MATLAB软件等构建数理模型并进行统计分析。本文采用自然对数形式来计算上证50 ETF的每日收益率。

2.2 模型评价

许多学者采用SV模型来研究波动率风险溢价，这可能是SV模型的结构及计算相较于SVCJ模型简便；本文将检验SV模型、SVJ模型及SVCJ模型在上证50 ETF市场中的拟合优度问题，从而选择最优模型。

Neumann等[18]使用DIC准则作为评价SVCJ模型、SVJ及SV模型拟合市场优劣程度的方法。DIC准则提供了模型复杂程度与拟合优度之间的一个权衡，DIC的值越小也就意味着模型的拟合优度更好。

接下来，将通过DIC准则从数值上来判断三者的拟合效果；通过计算，DICSV=2846，DICSVJ=2735，DICSVCJ=2676，SV模型的DIC值最大，SVJ模型其次，SVCJ模型的DIC值最小；因此，SVCJ模型相较于SV模型及SVJ模型具有更好的市场拟合优度。

3 实证研究

3.1 参数估计

如表1所示，SVCJ模型在P测度和Q测度下估计的参数。

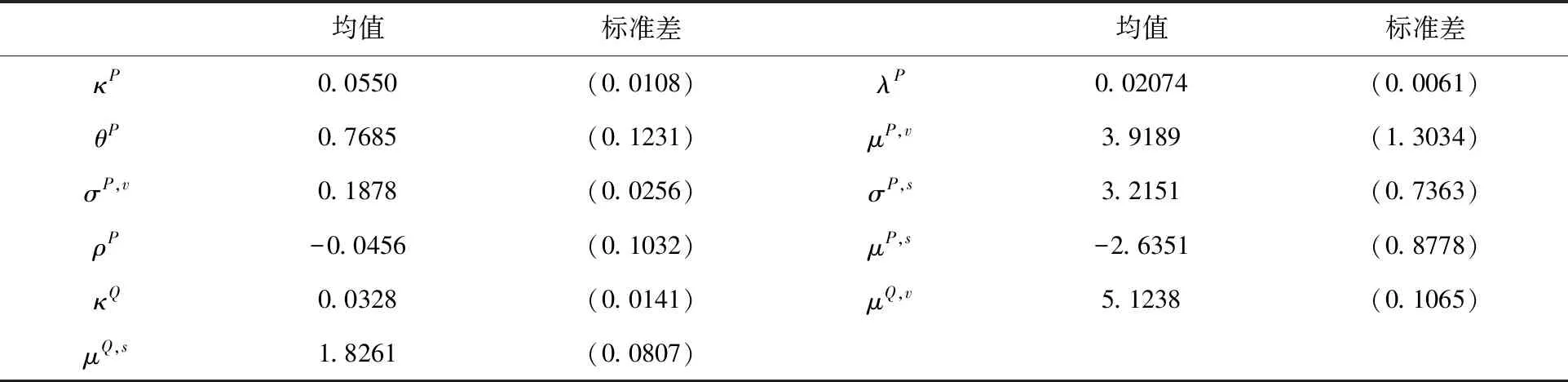
表1 参数估计

表1中的参数蕴含了一些市场特征；上证50 ETF波动具有均值回归特征，其均值回归速度κP=0.0550，ρ<0表明资产收益与波动之间存在“杠杆效应”，即资产价格下降时，常常伴随着较大的波动；λP=0.02074，说明资产收益发生跳跃并非常发生的事件；比较P测度与Q测度的模型中的参数，两者存在差异，说明资产收益及波动在两概率测度下呈现出不同的特性。

接下来，讨论SVCJ模型中波动率风险参数的估计效率问题。在前文的参数估计方法介绍中已将Q测度下波动率风险溢价的参数估计方法分为“Duffie法”和“FFT法”两类方法；参数估计在AMD Ryzen7 1700、Nvidia GeForce GTX1060 6G、8G ARM计算机上实现；从参数估计效率来说，采用“FFT法”需大约0.5 hours，而采用“Duffie法”需大约16 hours，显然“FFT法”具有更高的参数估计效率；从期权定价精度来说，先将两类方法估计的参数分别代入SVCJ模型中计算样本中每个期权合约的价格，再将计算得到的期权价格与实际期权交易价格对比(式(23))，RMSEFFT=3.61%，RMSEduffie=3.69%，两者的定价精度接近；总而言之，本文使用“FFT法”能显著提高波动率风险溢价的估计效率。

均方根误差(RMSE)公式:

(23)

其中，均方根误差(RMSE)反应了模型计算的期权价格与实际市场价格的偏离程度，误差值越小越好，其广泛应用于模型评价；n代表参与计算的期权合约个数，n=10900；Pmodel代表使用“FFT法”或者“Duffie法”计算的期权价格；Pmarket代表期权市场的实际价格。

3.2 波动率风险溢价的时变特征

在讨论波动率风险溢价的时变特征之前，先讨论样本区间内中国内地证券市场的基本情况。上海证券交易所推出上证50 ETF期权不久之后，中国内地市场经历了“千股跌停，千股停牌，千股复牌，千股涨停”的动荡时期，因此，本文将总样本区间划分为市场急剧动荡时期(2015.3.01～2016.3.30)和市场非急剧动荡时期(2016.4.1～2018.6.30)两个区间来讨论；首先，讨论上证50 ETF价格和收益率、收益跳跃和波动跳跃、GARCH波动率在两区间的基本情况；然后，再讨论对应区间的波动率风险溢价情况。

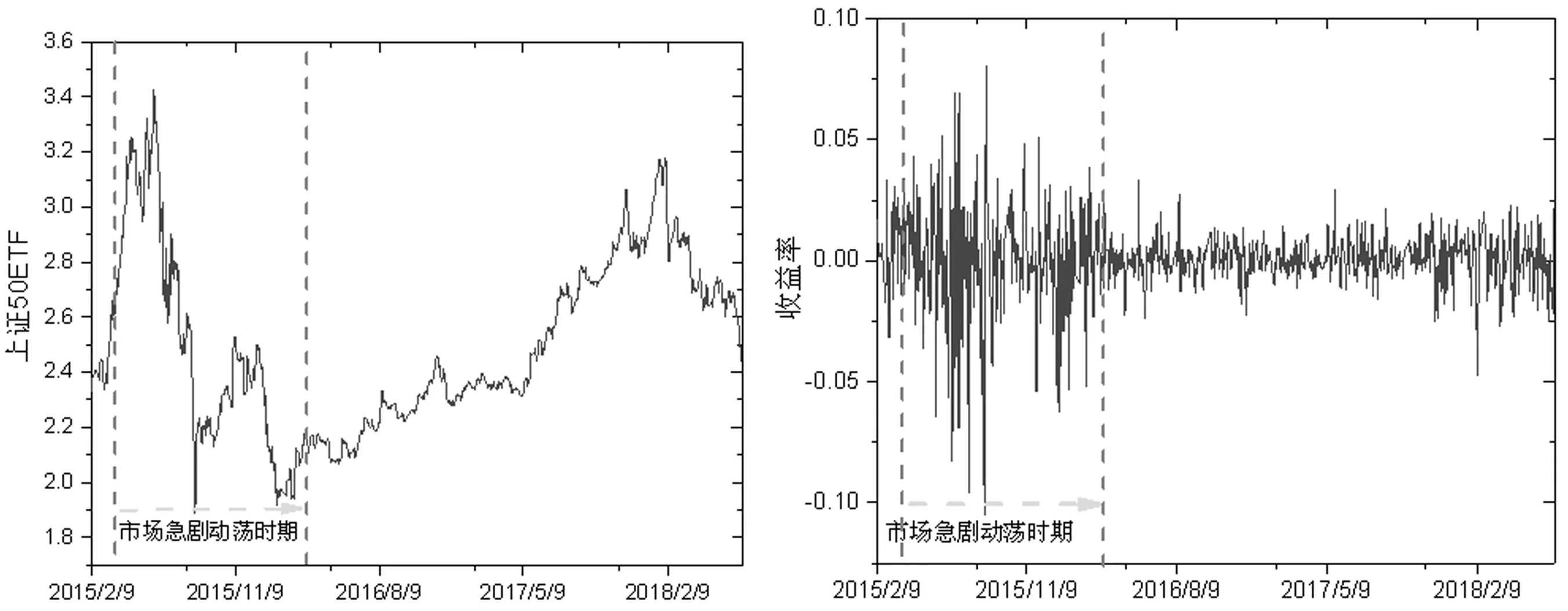
图1 上证50 ETF价格(左)及收益率(右)

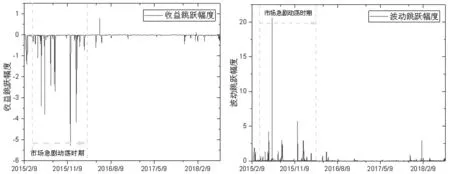
图2 上证50 ETF收益及波动跳跃幅度

如图1所示，在市场急剧动荡时期，ETF价格经历了“过山车”式的急剧动荡情况，此时的ETF收益率同样震荡明显，此后，上证50 ETF基本处于慢牛或盘整的非急剧动荡时期。如图2所示，在市场急剧动荡时期，上证50 ETF收益及波动均发生明显的跳跃而且跳跃幅度较大，而在市场趋于平稳的时期，ETF跳跃幅度也相对较小，这与国外学者研究其他市场的情况基本类似(Larsson K[28])。如图3(左)GARCH波动率所示，其中波动率构建采用GARCH(1,1)模型求得，通过实证分析表明GARCH(1,1)中各参数均在1%显著性水平下显著，与图1及图2走势图对应，在市场急剧动荡时期，波动率呈现大起大落的动荡特征，之后，市场波动率相对较小，整体相对平稳。接下来，将讨论市场急剧动荡时期和市场非急剧动荡时期的波动率风险溢价。

吴鑫育等[23]研究表明当波动率风险溢价为正时，投资者是偏好波动风险的，当波动率风险溢价为负时，投资者是厌恶波动风险的。Carr和Wu等[26]、Duan等[19]、Tim Bollerslev等[27]及Bekaert等[11]等研究表明S&P500期权市场的波动率风险溢价为负，投资者是厌恶波动风险的。上证50 ETF期权市场的波动率风险溢价是否同样如此呢？接下来，本文将讨论上证50 ETF期权的波动率风险溢价的时变特征及其蕴含的经济学解释。

第一，在市场急剧动荡时期(图3(左))，波动率风险溢价基本为负数；这是由于期权价格与波动率是同向变动的，在证券市场急剧动荡时期，投资者对期权的需求较大，期权价格上涨，而根据波动率风险溢价的定义可知，标的资产在P测度下的已实现波动率期望小于Q测度下的隐含波动率期望，投资者对标的资产未来的波动预期较高，而期权定价是在Q测度下进行的，因此，期权价格偏高，即投资者购买期权对冲波动风险而愿意支付的风险价格偏高，更直白地说，当市场急剧波动时，购买期权是一种有效的对冲手段，可用于规避市场波动风险，投资者也愿意为此支付偏高的风险价格，因此波动率风险溢价是负的，负的波动率风险溢价体现了中国内地金融市场投资者在市场急剧动荡时期总体上是厌恶波动风险的；而且市场越动荡，投资者对波动风险的厌恶程度越高，其更愿意为规避波动风险而支付的风险价格越偏高，波动率风险溢价在数值上也越小(波动率风险溢价“负”的越多)。

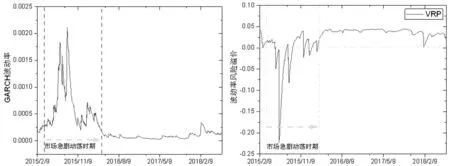
图3 GARCH(1,1)波动率(左)和波动率风险溢价(右)

第二，在非市场急剧动荡时期(图3(左))，波动率风险溢价基本为正，这与Tim Bollerslev等[27]及Bekaert等[11]等研究的美国成熟资本市场有所不同。为什么会出现这种情况呢？其实也不难解释：中国内地证券市场起步相对较晚、发展尚不完善、散户比例高且缺乏理性的投资理念(乔柯南等[29])，因此，在非急剧动荡时期，投资者愿意承受标的资产的波动，少量或者不购买期权对冲市场波动风险，因此，标的资产在P测度下的已实现波动率期望大于Q测度下的隐含波动率期望，投资者对未来标的资产的波动预期较低，此时期权定价偏低，即投资者购买期权对冲波动风险而愿意支付的风险价格偏低，即波动率风险溢价为正，投资者总体呈偏好波动风险的态度。

综上可知：1)上证50 ETF期权的波动率风险溢价具有明显的时变特征且不恒为零。2)从波动率风险溢价的数值上来说，波动率风险溢价在数值上越小，则表示投资者对冲市场波动风险的意愿越高；波动率风险溢价在数值上越大，则表示投资者对冲市场波动风险的意愿越低。3)从波动率风险溢价的“正”“负”及蕴含的投资者态度来说，在市场急剧动荡时期，波动率风险溢价基本为负，投资者是厌恶波动风险的；而在市场非急剧动荡时期，波动率风险溢价基本为正，投资者是偏好波动风险的；波动率风险溢价能够监测到中国内地证券市场的投资者波动风险态度的改变，另外也说明投资者的波动风险态度也具有时变特征，即投资者的波动风险态度并非总是偏好或厌恶的。

3.3 波动率风险溢价的影响因素

通过前面的研究发现，波动率风险溢价具有明显的时变性，而波动率风险溢价的变化可能是由多种因素作用的结果。目前关于波动率风险溢价的研究大多集中于波动率风险溢价的估计上，影响因素的研究相对较少；陈蓉等[6]研究表明恒生指数收益率与波动率风险溢价显著负相关，波动率与波动率风险溢价显著负相关；郑振龙[24]认为换手率可作为投资者异质信念的代表，异质信念越高，意味着市场暴跌等极端风险出现的可能性增大，研究表明换手率与波动率风险溢价显著负相关；Chen等[2]和郑振龙等[24]讨论了投资者情绪与波动率风险溢价的关系，研究表明恐慌情绪与波动率风险溢价显著负相关。

根据上述研究，本文主要从市场波动率、收益率、投资者情绪等市场微观结构分析其对波动率风险溢价的影响。收益率、波动率及换手率均来自上证50 ETF市场；本文选取上海证券交易所基于上证50 ETF期权推出的iVIX指数(又称“恐慌指数”)作为投资者情绪指标，其蕴含着投资者的情绪，当iVIX指数上涨时，市场中的恐慌情绪上涨。

基于上述分析，本文提出基本假设：

H1收益率与波动率风险溢价正相关，即收益率越高，波动率风险溢价越高。

H2波动率与波动率风险溢价负相关，即波动率越高，波动率风险溢价越低。

H3换手率与波动率风险溢价负相关，即换手率越高，波动率风险溢价越低。

H4投资者情绪与波动率风险溢价负相关，即投资者情绪越高，波动率风险溢价越低。

表2 描述性统计

注：*表示10%的显著性水平下显著、**表示5%的显著性水平下显著、***表示1%的显著水平下显著。

首先，本文采用ADF单位根检验变量的平稳性，表2中表明所选变量是平稳的。

表3 相关性及多重共线性检验

接着，讨论自变量之间的多重共线性问题，由表3可知，各自变量之间也存在一定的相关性，为了避免多重共线性问题，本文还使用方差膨胀因子来检验回归变量的多重共线性问题，由表3 VIF检验可知，各变量的方差膨胀因子值(VIF)均小于10，因此各变量之间不存在多重共线性问题；最后，构建线性回归模型，建立模型如下：

VRPt=c+α1returnt-1+α2Volatilityt-1+

α3Turnovert-1+α4iVLXt-1+εt

(24)

式(24)中α1-4为变量系数、εt为误差项、returnt-1为上证50 ETF前一期收益率、Volatilityt-1为使用GARCH(1,1)构建的前一期波动率(陈蓉等[6])，为了避免变量大小引起失衡，将波动率放大100倍；Turnovert-1为上证50 ETF前一期换手率；iVIXt-1为前一期投资者情绪，为了避免变量大小引起失衡，将iVIXt-1的值缩小100倍。

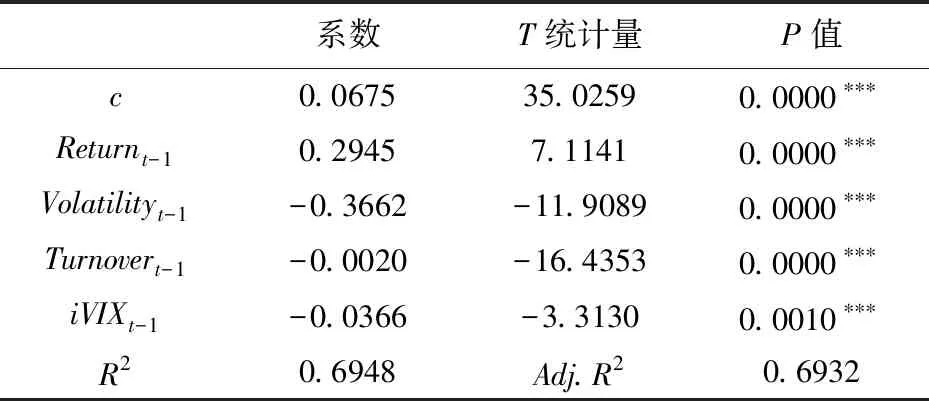
表4 回归结果

注：*表示10%的显著性水平下显著、**表示5%的显著性水平下显著、***表示1%的显著水平下显著。

收益率对波动率风险溢价的影响在1%的水平上显著为正，与假设H1一致。当市场收益率上涨时，波动率风险溢价在数值上变大，投资者购买期权对冲波动风险的意愿变低；当市场收益率下跌时，波动率风险溢价在数值上变小，投资者购买期权对冲波动风险的意愿变高。

波动率对波动率风险溢价的影响在1%的水平上显著为负，与假设H2一致。当市场波动剧烈时，市场中的不稳定性也相应增加，波动率风险溢价在数值上变小，投资者更愿意购买期权对冲波动风险。

换手率与波动率风险溢价的影响在1%的水平上显著为负，与假设H3一致；当市场换手率越高，投资者异质信念程度越高，意味着市场暴跌等极端波动风险出现的可能性增大，波动率风险溢价在数值上变小，投资者更愿意购买期权对冲波动风险。

投资者情绪对波动率风险溢价的影响在1%的水平上显著为负，与假设H4一致。这是由于iVIX指数上涨，市场中弥漫着“恐慌情绪”，投资者对未来市场波动预期变大，其避险意识上升，波动率风险溢价在数值上变小，投资者购买期权对冲波动风险的意愿变高；相反，当iVIX指数下跌时，说明投资者对未来市场持有相对乐观的心态，波动率风险溢价在数值上变大，投资者购买期权对冲波动风险的意愿变低。

4 结论

本文运用上证50 ETF及其期权市场日频交易数据，采用SVCJ模型及MCMC、傅里叶变换法等方法，从P测度及Q测度中提取波动率风险溢价，研究结果如下：

首先，SVCJ模型相较于SV模型、SVJ模型具有更好的市场拟合优度；采用傅里叶变换法能提高波动率风险溢价的估计效率；

其次，波动率风险溢价具有时变特征。在市场急剧动荡时期，投资者购买期权对冲波动风险意愿较高，期权价格大幅上涨，期权定价偏高，因此，波动率风险溢价是负的，负的波动率风险溢价体现了投资者在市场急剧动荡时期总体上是厌恶波动风险的。在市场非急剧动荡时期，投资者购买期权对冲波动风险的意愿较低，期权需求较低，期权价格偏低，波动率风险溢价为正，正的波动率风险溢价体现了投资者在市场非急剧动荡时期总体上是偏好波动风险的；

最后，本文研究波动率风险溢价的影响因素。收益率对波动率风险溢价的影响显著为正，当市场收益率上涨时，投资者购买期权的意愿变低；波动率对波动率风险溢价的影响显著为负，当市场波动变大时，投资者购买期权的意愿变高。换手率对波动率风险溢价的影响显著为负，换手率越高，投资者异质信念程度越高，意味着市场暴跌等极端波动风险出现的可能性增大，投资者购买期权的意愿变高。投资者情绪对波动率风险溢价的影响显著为负，当市场中的“恐慌情绪”增大时，购买期权能为投资者提供风险保护，投资者购买期权的意愿变高。

上证50 ETF期权是中国内地主要的场内大型交易的期权，其运行状况及蕴含的信息特征将会为后续推出指数期权、期货期权、个股期权、波动率衍生品等提供重要参考；另外，文本的研究也为投资者构建合理的投资决策、相关部门的风险管理提供参考。