资产剥离对风险溢价的影响研究

陈 佳， 李 强， 曾 勇

(电子科技大学 经济与管理学院，四川 成都 611731)

0 引言

自Boudreaux[1]首次结合股票市场反应考察资产剥离以来，作为母公司处置或出售资产、设施、生产线、附属机构或业务部门的一种决策行为[2]，资产剥离及其对企业的影响一直是学术研究的热点。相关研究可概括为两个方向：一类文献主要利用美国[3,4]、欧洲[5]、韩国[6]等不同市场的数据，实证考察资产剥离的短期市场反应，并一致发现剥离公告对母公司股价具有正向影响的证据。另一类文献主要从剥离冗余资产利于优化治理结构与节约管理成本[7,8]、调整规模便于应对经济技术的外部环境变化[9,10]、剥离所得和管理资源可以重新聚焦新的资产或核心资产[11～13]等多个角度，理论上分析资产剥离改善企业盈利状况和提升企业价值的作用。然而，需要指出的是，无论是关于短期市场反应的实证考察，还是资产剥离影响企业价值的机理研究，都未涉及资产剥离行为如何作用于资产的风险收益特征。

事实上，将企业总资产分解为在位资产和增长期权两个部分，关于资本支出[14～16]和R&D投资[17]影响资产风险溢价的已有研究表明，企业决策行为可以通过改变资产的相对构成而影响资产的风险收益特征。对于资产剥离行为而言，无论是收缩资产规模还是直接出售资产，都会影响或改变在位资产内部的相对构成和总资产中在位资产的相对构成，进而也对资产风险收益特征具有重要影响。仅有的文献Cooper和Priestley[18]、张莹春[19]给出了资产负增长对股票预期收益具有正向影响的证据，但嵌入于在位资产的资产剥离到底如何作用于资产的风险收益特征，目前尚缺乏相关的理论研究。

将资产出售刻画为一种看跌期权，Hackbarth和Johnson[20]理论上指出了收缩和扩张两种运营决策会共同导致资产风险溢价的动态变化。但是，不同于被刻画为看跌期权的资产出售行为[21～23]，现实中企业在资产剥离的同时，通常会考虑如何将剥离所回收的资本、管理资源等重新聚焦于核心资产。从这个意义上讲，已有研究讨论的资产出售只是资产剥离的一种特殊情形，更为一般的资产剥离本质上可看作一种交换期权：标的资产为剥离带来的核心资产价值增量，执行价格为拟剥离的非核心资产价值。相应地，资产剥离行为对风险溢价的动态影响应该由剥离前资产的相对构成和各部分资产风险溢价的相对大小，以及交换期权的灵活性价值共同决定。进一步，由于资产剥离是针对在位资产的一种决策，那么，企业是否拥有剥离决策的灵活性，以及在位资产和增长期权构成比例不同的企业生命周期阶段，都会使得资产剥离对风险溢价的影响表现有所不同。

鉴于已有关于资产剥离影响风险溢价的理论文献尚为缺乏，同时注意到现实中资产剥离并非只是简单地进行资产出售，本文考虑企业通过剥离非核心资产而聚焦核心资产的情形，将资产剥离决策视作一种交换期权，从影响方向和影响程度两个层面理论上剖析资产剥离作用于风险溢价的机理，并利用沪深两市1998～2016年间1342家发生资产处置的非金融类A股上市公司数据，进行实证检验。研究结果表明，资产剥离会提升还是会降低风险溢价，取决于非核心和核心资产风险溢价的相对大小：如果核心资产的风险溢价高于非核心资产，资产剥离将提升风险溢价；反之降低风险溢价。进一步，资产剥离的影响程度由两类资产价值占比的差异和交换期权的价值占比共同决定：两类资产的价值占比差异越大，资产剥离的影响越大；交换期权的价值占比越高，资产剥离的影响越弱。此外，扩展研究的结论表明：延迟等待的剥离决策灵活性会削弱资产剥离的影响；年轻阶段企业进行资产剥离更加可能对风险溢价具有提升作用。

后续结构安排如下：第一节是基本假设；第二节运用实物期权方法求解资产价值；第三节利用定价核技术给出资产风险溢价及其构成的解析表达，并重点分析资产剥离对风险溢价的影响；第四节为模型扩展与讨论；第五节为实证检验；最后是结束语。

1 基本假设

考虑一家代表性企业，资产包括盈利能力不同的1个单位核心资产和1个单位非核心资产，两类资产的现金流过程分别服从：

(1)

(2)

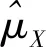
假设企业剥离1个单位非核心资产的同时，会将剥离回收的资本和管理资源等重新投入到核心资产，剥离完成后的核心资产现金流X(t)将提升至原来的1+k倍，参数k的大小可以反映资产剥离提升核心资产盈利能力的效果，现实中由剥离成功的概率、剥离所需付出的成本、以及剥离后企业的整合能力等共同决定。完成非核心资产剥离后，企业价值仅由盈利能力提高了的1个单位核心资产构成，从而资产剥离行为可以视作一个交换期权：标的资产为盈利能力提高所带来的核心资产价值增量，执行价格为被剥离掉的1个单位非核心资产价值。

假设外生的定价核服从：

dΛ(t)=-rΛ(t)dt+φΛ(t)dZ(t)

(3)

dX(t)=μXX(t)dt+σXX(t)dWX(t)

(4)

dY(t)=μYY(t)dt+σYY(t)dWY(t)

(5)

2 企业价值及构成

2.1 在位资产价值

企业进行资产剥离之前，核心资产和拟剥离的非核心资产价值分别为各自现金流X与Y的永续折现值：

2.2 资产剥离的交换期权价值

对于非核心资产，一旦其现金流相对于核心资产现金流低于某个水平，企业将择机进行剥离，而后将剥离所得投资于核心资产。该决策可以视作一种交换期权，其中：标的资产为核心资产的价值增量，执行价格为剥离掉的非核心资产价值。借鉴Dixit和Pindyck[24]的做法，交换期权的价值满足贝尔曼方程:

VD(X,Y)=max{e-rdtEt[VD(X+dX,Y+dY)],

(8)

式中，第一部分表示继续等待时机以执行交换期权的价值，第二部分表示立即执行交换期权的价值。运用伊藤引理展开并化简式(8)可得偏微分方程:

(9)

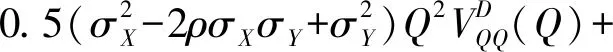
(10)

且满足边界条件:

(11)

(12)

(13)

根据三个边界条件(11)～(13)，方程(10)的交换期权价值为：

(14)

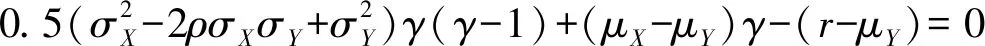
(15)

2.3 企业总价值

至此，进行资产剥离前拥有交换期权的企业价值可以表示为：

V0(X,Y)=VP(X)+VU(Y)+VD(X,Y)

(16)

式中，(Q/Q*)γ1反映企业进行资产剥离的概率，其大小由拟剥离的非核心资产和核心资产的现金流特征共同决定。特别地，在剥离执行临界值点Q*处，容易有∂V0/∂Q|Q=Q*>0，即非核心资产的剥离会导致企业价值的提升，这可以解释已有文献中资产剥离会导致短期市场正向反应的实证证据。

剥离非核心资产之后，企业资产由盈利能力提高为原来1+k倍的1个单位核心资产构成，相应的企业价值为：

(17)

参照Carlson等[15]以及Dixit和Pindyck[24]，设定基本参数为：Y=5，μX=0.02，μY=-0.01，σX=σY=0.2，r=0.05，ρ=0.2，k=1，图1给出了资产剥离前后企业价值及其各部分构成动态变化的数值示例。由图可见：给定非核心资产的现金流水平，随着核心资产现金流水平的增加，剥离前核心资产和交换期权的价值逐渐增加；一旦企业于剥离临界值Q*=1.7472处执行交换期权后，总资产将全部由核心资产构成。

图1 资产剥离前后资产价值及各构成部分随核心资产现金流水平的变化

3 资产剥离对风险溢价的影响

3.1 资产风险溢价及构成

在得到企业总资产各部分价值的基础上，本节将采用随机贴现因子方法计算相应的风险溢价。根据Cochrane[27]，价值为V的任意资产的风险溢价表达式为:

(18)

将式(6)、式(7)及式(14)的上半支分别代入，并运用伊藤引理化简可得核心资产、非核心资产和交换期权的风险溢价分别为:

E(RP)=θX

(19)

E(RU)=θY

(20)

E(RD)=γ1θX+(1-γ1)θY

(21)

由式(21)可以看出：交换期权的风险溢价可以表示为非核心和核心两类资产风险溢价的加权平均，权重分别为γ1和1-γ1；而且，由于γ1>1，“做空非核心资产、做多核心资产”的交换期权具有杠杆特征，γ1大小可以反映杠杆倍数。特别地，若θX=0，式(21)的E(RD)<0，表明交换期权的风险溢价为负，模型将退化为Lambrecht和Myers[21]讨论的企业停止运营的极端情形，交换期权也相应地退化为看跌期权。

将各部分风险溢价表达式(19)～式(21)按其相应价值占比进行加权平均有:

(22)

可以看出，交换期权正是通过影响非核心和核心两类资产现金流波动对总资产风险的贡献大小而发挥杠杆作用，具体方向取决于θX和θY的相对大小：若θX≥θY，交换期权的杠杆对总资产风险溢价具有正向作用；反之，若θX<θY，交换期权具有负向作用。从式(22)第二行θX和θY前面的系数还可以一致发现，γ1越大、价值占比越高，两类资产现金流波动对总资产风险的贡献受交换期权的影响越大。

一旦完成资产剥离，企业总资产全部为核心资产，相应的风险溢价为：

E(R1)=E(RP)=θX

(23)

在图1的基础上，进一步设定参数φ=0.4、ρY=-0.5，ρX=-0.45(θX<θY)、ρX=-0.55(θX>θY)，图2针对θX<θY和θX>θY两种情形，给出资产剥离前后风险溢价动态变化的数值示例。随着X进而Q=X/Y的逐渐增加，风险溢价在θX<θY和θX>θY两种情形下分别逐渐降低和提高，究其原因在于：在θX>θY的情形下，交换期权的杠杆作用使得E(RD)≥θX≥θY，同时随着Q的增加，交换期权的价值占比逐渐增加，进而剥离前风险溢价呈现上升趋势，并在资产剥离后维持在核心资产的风险溢价水平；θX<θY的情形反之类似。

图2 资产剥离前后风险溢价随核心资产现金流水平的变化

3.2 资产剥离前后风险溢价的变化

参照Carlson等[28]的做法，将式(23)和式(22)做差，资产剥离对风险溢价的动态影响可以表示为:

ΔE(R)=E(R1)-E(R0)

(24)

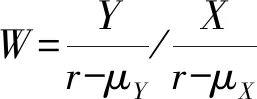
其一，资产剥离到底会提升还是降低风险溢价，取决于非核心和核心两类资产风险溢价的相对大小。特别地，如果核心资产的风险溢价高于拟剥离的非核心资产(即θX≥θY)，剥离会提升风险溢价，即ΔE(R)≥0，这可以解释已有文献关于资产负增长和股票预期收益具有正向关系的实证证据[18,19,29]。

其二，资产剥离的影响程度取决于剥离前资产的相对构成。记

(25)

容易证明:

(26)

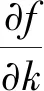
(27)

式(26)表明，剥离前非核心和核心两类资产价值占比的差异越大，剥离对风险溢价的影响程度越大；式(27)则表明，k越大，剥离前交换期权价值及其占比越高，在交换期权降低非核心资产风险贡献的作用下，剥离非核心资产后其对总资产风险贡献的消失最终造成的影响越小。

此外，对于参数γ1，尽管杠杆倍数本身越大，但交换期权价值及其价值占比越小，γ1对资产剥离影响程度的作用并不确定。

4 扩展与讨论

4.1 NPV规则下的资产剥离

作为对比，考虑企业没有延迟决策灵活性的特殊情形。该情形下，企业利用净现值(NPV)规则立即做出剥离决策，此时交换期权的价值VD=0，从而式(24)退化为：

(28)

对比式(28)和式(24)，可以发现：NPV规则下，资产剥离的影响方向同样取决于核心和非核心两类资产风险溢价的相对大小，影响程度则只取决于剥离前两类资产价值的相对占比。更为重要的是，式(28)θX-θY前的系数少了-(γ1-1)VD/V0，因此，NPV规则下，由于不存在交换期权及其杠杆作用，资产剥离对风险溢价的影响程度更大，从这个意义上讲，延迟等待的剥离决策灵活性会削弱资产剥离的影响。

4.2 不同生命周期阶段的资产剥离

上节结论表明，资产剥离会通过改变核心和非核心资产的相对构成而对风险溢价产生影响。更为一般的情形下，除了在位资产，企业总资产同时还包括未来有待投资的增长期权[30]，二者相对构成随企业生命周期推的不断变化也会使得嵌入于在位资产的资产剥离对风险溢价的影响将在不同生命周期阶段会表现得有所不同。

为此，本节将企业的生命周期阶段划分为资产构成比例不同的年轻和成熟两个阶段，扩展讨论不同阶段进行剥离对总资产风险溢价的影响差异。在年轻阶段，企业资产包括1个单位核心在位资产、1个单位拟剥离的非核心在位资产，以及1个单位待投资的增长期权。简化起见，假设增长期权标的资产的现金流过程与核心在位资产相同。伴随着增长期权的执行，企业由年轻进入成熟阶段，届时总资产由2个单位核心在位资产和1个单位非核心在位资产构成。

对于标的资产与核心在位资产现金流特征相同的增长期权，其价值满足贝尔曼方程：

VG(X)=max{e-rdtEt[VG(X+dX)],VP(X)-I}

(29)

式中，第一部分表示继续等待时机以执行增长期权的价值；第二部分表示立即执行增长期权的价值。运用伊藤引理展开上式可得微分方程:

(30)

且满足边界条件：

(31)

(32)

(33)

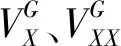
(34)

其中：上半支表示增长期权等待执行的价值；下半支为立即执行的价值；执行临界值和待定系数β分别为：

(35)

(36)

在生命周期的年轻阶段，资产剥离前的企业价值可以表示为:

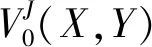
(37)

其中，VG(X)和VD(X,Y)分别取自式(34)和式(14)的上半支。一旦企业对非核心资产进行剥离，年轻企业的价值为现金流提高后的核心在位资产和增长期权价值之和：

(38)

同理，在生命周期晚期的成熟阶段，资产剥离前后的企业价值分别为:

(39)

(40)

采用与上节类似的方法，将式(34)上半支代入式(18)，容易得到年轻阶段企业的增长期权风险溢价为：

E(RG)=βθX

(41)

根据资产剥离前后各部分资产的价值占比，可将企业年轻阶段资产剥离前后的风险溢价分别表示为：

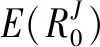
(42)

(43)

进而年轻阶段资产剥离对风险溢价的影响为:

(44)

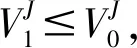
同理，在生命周期晚期的成熟阶段，企业进行资产剥离对风险溢价的影响为:

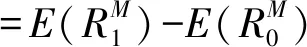
(45)

对比式(44)和式(45)可以看出：伴随增长期权执行企业进入成熟阶段后，资产剥离对风险溢价的影响仅取决于在位资产内部非核心和核心资产的相对构成。因此，从企业生命周期的角度来看，相对于成熟阶段，企业在年轻阶段进行的资产剥离更加可能对风险溢价产生正向影响。

图3 不同生命周期阶段资产剥离对风险溢价的影响

在图2的基础上，给定增长期权执行成本I=150，图3给出了年轻和成熟阶段进行资产剥离对风险溢价的影响随Q动态变化的数值示例。对比年轻和成熟两种情形可以发现，不管θX和θY的相对大小关系如何，拥有增长期权的年轻企业进行资产剥离导致的风险溢价的变化曲线都在成熟企业的上方，这说明企业在年轻阶段进行资产剥离更加可能对风险溢价产生正向影响。此外，对比θX>θY和θX<θY两种情形，图3(a)和图3(b)中资产剥离分别具有正向和负向影响，而且，随着Q=X/Y的逐渐增加，在位资产中非核心和核心两类资产价值占比的差异W逐渐降低，根据式(25)，资产剥离对风险溢价的影响程度逐渐减弱，表现为图(a)和图3(b)中风险溢价的变化分别从负向和正向趋近于0。

5 实证检验

5.1 数据、样本与变量

本节利用1998～2016年间发生资产剥离的1342家沪深两市非金融类A股上市企业数据，剔除退市、净资产小于0和所有变量有缺失的样本，并参照徐虹[31]剔除了剥离金额在1000万以下的样本，以及对所有连续变量进行首尾1%的缩尾处理，最终得到1342家企业、216个月共52843个企业-月度观测值。相关数据均来自国泰安CSMAR数据库。

在变量定义与测度方面，个股预期收益率利用下一个财务年度1 月至12月的考虑现金红利再投资的月度收益率测度；关于资产剥离，利用处置固定资产、无形资产和其他长期资产所收回的现金净额除以总资产测度剥离强度。与此同时，由于无法获知样本企业核心和非核心的资产构成，我们利用营业内收入占营业总收入的比例作为非核心与核心两类资产价值占比差异的代理变量，该比例越高说明两类资产的价值占比越接近，进而非核心与核心资产的价值占比差异越大。资产剥离的决策灵活性方面，我们利用固定资产占总资产的比例作为代理变量，该比例越高表示企业越可能进行剥离，进而剥离决策的灵活性价值越大。企业生命周期的测度方面，利用企业IPO上市至考察年度的年份之差度量企业年龄。控制变量方面，包括市场贝塔、账面市值比和市值规模[32]。所有变量的具体定义详见表1。

表1 变量定义与指标测度

5.2 描述性统计结果

在每个财务年度，根据剥离强度中位数，将该年度样本分为两组；进一步，按照每年的营业收入占比和固定资产占比的中位数，以及样本期内企业上市年龄的中位数，进一步对剥离强度大小两组子样本进行二维分组，分别构造2×2的四个等权投资组合，并利用组合下一财务年度1～12月的月度收益率测度组合的预期收益率。表2给出了各组合预期收益率的描述性统计及均值差异性检验结果。

由表2可见：相对而言，剥离强度较高的企业预期收益总是高于剥离强度较低的企业；进一步，对于营业收入占比较低、固定资产占比较低、上市年龄较小的组合，剥离强度大小差异导致的组合预期收益的差异总是要高一些，且在上市年龄小的组合中，这种差异在统计意义上是显著的，进而初步支持上节的理论预示：非核心与核心两类资产的价值占比的差异越大、剥离决策的等待灵活性价值越小、企业越年轻，资产剥离强度对股票预期收益的正向影响越大。

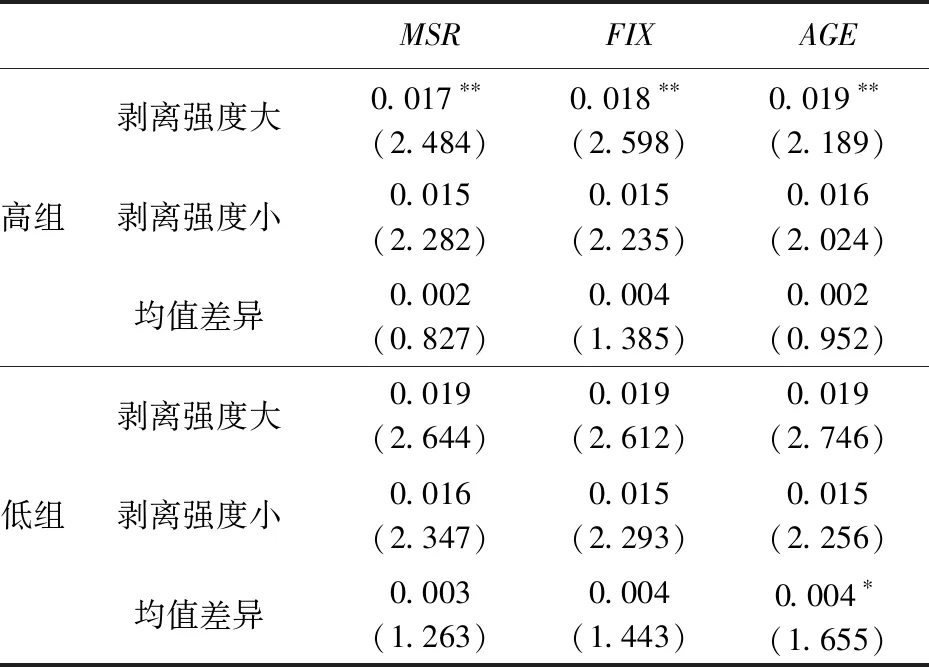
表2 组合预期收益率的描述性统计及差异性检验

注：括号内为T值，***、**、*分别表示在1%、5%和10%的水平上显著，下同。

5.3 Fama-Macbeth回归结果

表3利用Fama-Macheth两步截面回归方法[33]，控制Fama-French三因素，给出全样本和不同子样本下资产剥离影响股票预期收益率的OLS回归结果，整体上得到支持前述理论预示的实证证据。

针对全样本的模型1回归结果表明，整体而言，资产剥离强度和股票预期收益率具有显著的正向关系，与已有文献的实证结果一致[18,19,29]。进一步，模型2针对营业收入占比高低分组子样本的回归结果显示：剥离对股票预期收益率的正向影响仅在营业收入占比较低的组别中才显著，这意味着剥离前非核心和核心两类资产价值占比的差异越大，剥离对风险溢价的影响程度越大。模型4关于固定资产占比高低分组子样本的回归结果显示：剥离对股票预期收益率的正向影响也仅在固定资产占比较低的组别中显著，即剥离的决策灵活性价值较低的情况下，剥离对风险溢价的影响更大；换言之，灵活性价值会削弱剥离的影响。模型6根据企业上市年龄分组子样本的结果显示：剥离对股票预期收益率的影响仅在上市年龄较小的组别中显著，即年轻企业进行的资产剥离更加可能提升风险溢价。

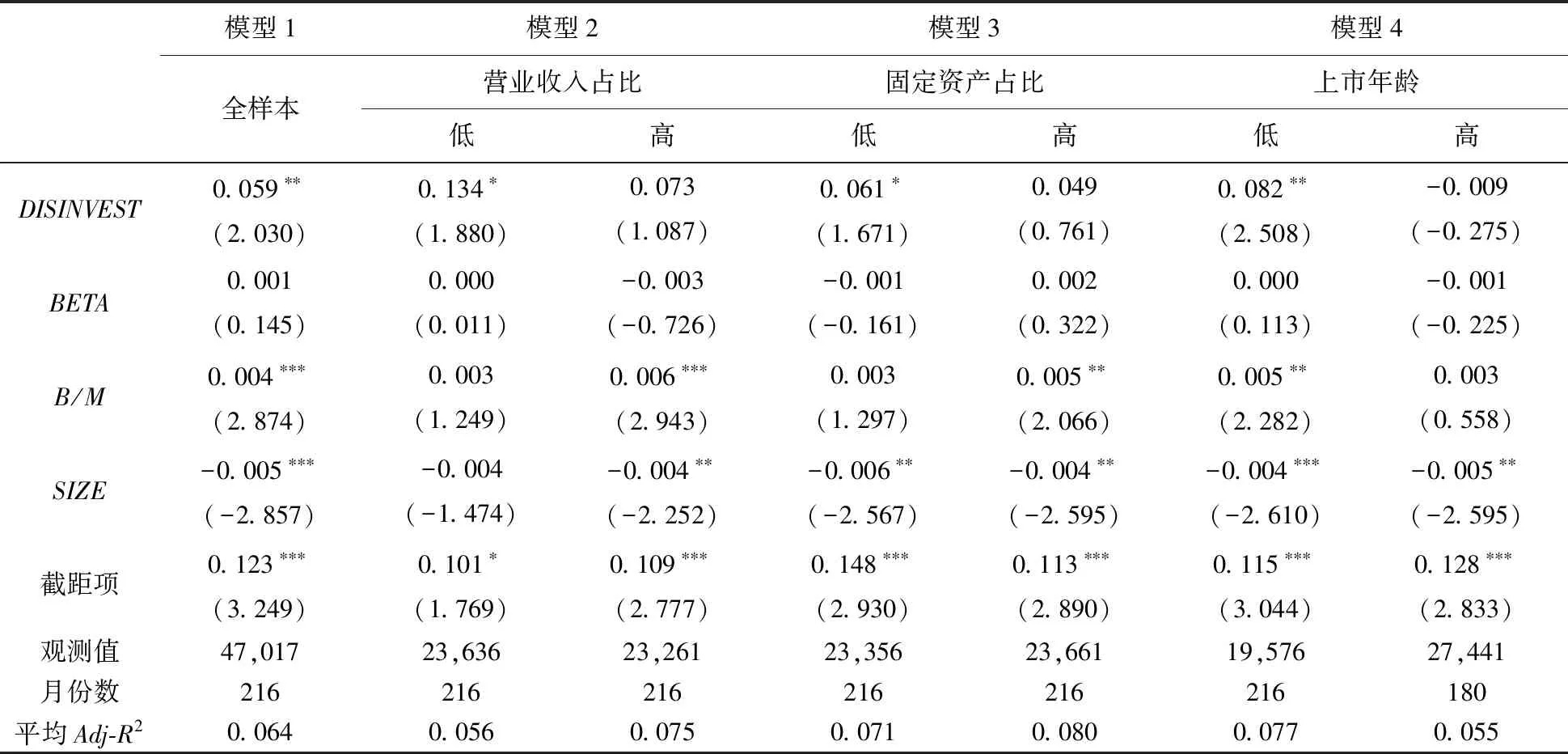
表3 Fama-Macbeth两步截面回归结果

6 结论

剥离非核心资产而将资源重新配置于核心资产的资产剥离会通过改变资产构成而影响资产的风险收益特征。本文将资产剥离模型化为一种交换期权，分析了资产剥离影响风险溢价的理论机理，并从决策灵活性和生命周期两个角度扩展讨论了企业特征差异所导致的资产剥离影响作用的不同，并进行了实证检验。研究结果表明：资产剥离对风险溢价的影响方向取决于非核心和核心两类资产风险溢价的相对大小，影响程度则由两类资产价值占比的差异和交换期权的价值占比共同决定：两类资产的价值占比差异越大，资产剥离的影响越强；交换期权的价值占比越高，资产剥离的影响越弱。此外，相对于NPV规则下的剥离决策，等待剥离的决策灵活性会削弱资产剥离的影响，年轻阶段较之成熟阶段进行资产剥离更加可能提升资产风险溢价。研究结果不仅为资产剥离短期市场反应和剥离影响股票预期收益率的已有实证证据提供了理性定价视角的一种可能解释，还丰富和扩展了企业运营决策和资产定价关系的研究。

未来的研究可进一步结合现金持有、创新投资、资本结构等企业决策行为，研究其与资产定价的关系，以及针对典型案例企业的具体资产构成状况，对企业剥离决策及其影响进行深入的案例研究。