一种机器人最优加速度轨迹规划算法研究
赵 亮, 仲 崇 权, 郑 飞 翔
( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024;2.华为数字技术有限公司, 江苏 苏州 215000 )
一种机器人最优加速度轨迹规划算法研究
赵 亮*1, 仲 崇 权1, 郑 飞 翔2
( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024;2.华为数字技术有限公司, 江苏 苏州 215000 )
针对机器人调试过程中遇到的超限问题,提出了一种满足运动约束的加速度最优T型速度曲线控制方法,利用拉格朗日法分析了码垛机器人的动力学性能,论述了机器人轨迹规划算法的实现过程.该算法在保证运动平稳的基础上,充分发挥了驱动关节的驱动性能.与传统速度曲线的对比表明,无论单轴还是轴组模式下,机器人的控制效果均得到了明显的提高.
码垛机器人;动力学;轨迹规划;最优加速度
0 引 言
机器人最优轨迹规划,即根据给定的路径点规划出通过这些点并满足边界约束条件的光滑的最优运动轨迹,是工业机器人最优控制问题之一[1-2].早期的轨迹规划研究多见于为了最大化操作速度从而减少最小化机器人总的动作时间[3-4],然而实际上,能量最优也是工业应用中很重要的性能指标.关节空间轨迹规划对机器人运动过程中的轨迹没有特别严格要求,只规定初末两点的位姿[5].在对机器人进行运动控制时,各个位置约束、速度约束、加速度约束是需要考虑的关键问题.当机器人运动速度较快时,驱动关节速度和加速度比较容易超限,导致驱动电流过大、位置偏差过大、超出限位等问题.因此,在对机器人进行轨迹规划时必须综合考虑速度和加速度等约束条件.
张丰华等在考虑运动约束的前提下,采用“4-3-4”法利用不同低阶多项式对各轨迹段进行插补,以实现流畅连续的自动码放货物的要求[6].徐海黎等在考虑运动约束前提下,以机器人运动过程中的总时间最优为目标,通过三次多项式插值进行型值点连接,使用加权函数法定义代价函数,研究其运动过程[1].Saravanan等在考虑运动约束的前提下,使用NURBS曲线规划机器人运动轨迹,通过优化时间来提高机器人的工作效率[7].Piazzi等在研究机器人运动过程中讨论了其冲击最小问题,在对机器人进行轨迹规划时,提高了机器人动力学性能[8].Zlajpah等精确地建立了机器人动力学方程,获得了满足运动约束的时间最优的运动轨迹,并在实际应用中验证了其可行性与正确性[9].
通过合理的轨迹规划可以使机器人运动过程中某项性能最优[10-12],本文以四自由度混联码垛机器人为研究对象,根据实际对象建立该机器人的运动学模型,研究其运动特性,分析其动力学性能,提出一种易于满足运动约束的最优加速度轨迹规划算法,以在保证机器人运动不超限的前提下,充分发挥驱动关节的驱动性能.
1 码垛机器人动力学模型
码垛机器人的动力学性能与各个杆件的加速度、杆件的质量分布、杆件的转动惯量以及机构的负载密切相关.为了提高机构的响应速度和可靠性,研究其动力学性能,对机器人进行动力学分析已经成为研究工作和设计的重点[13-14].在码垛机器人的实际调试过程中,加速度的大小对机器人的控制效果影响较大,所以寻找一段最优加速度轨迹具有重要意义.
针对码垛机器人含有局部闭链的平行四连杆的机械结构,选取拉格朗日法建立码垛机器人的动力学方程,如图1所示为码垛机器人臂部结构的运动简图,大臂转动的角度为α,小臂转动的角度为β,作为系统的广义坐标,可描述该二自由度系统.杆件CE、杆件BC、杆件AD、杆件DF的长度分别为lb、lc、la+lb、lc+ld.对于n个连杆组成的机器人,由拉格朗日函数描述的系统动力学方程为
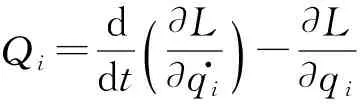
Qi=ddt(∂L∂q.i)-∂L∂qi
(1)
式中:L为拉格朗日函数;Qi表示作用在第i个关节的广义驱动力矩,i=1,2,…,n;qi(i=1,2,…,n)为使系统具有完全确定位置的广义关节变量;

q.
i为广义坐标qi对时间t的一阶导数,即相应的广义关节速度.

图1 码垛机器人臂部结构
建立广义坐标α、β与两个移动关节在基坐标系的位置关系.以腰部某点建立基坐标系,机身某点建立参考坐标系O-xyz,竖直移动滑块的位置坐标为(0,za)、水平移动滑块的位置坐标为(xc,0).杆件BC长度为lc,杆件AB长度为la,根据分析可知

(2)

(3)
可以得到系统的动力学方程为

(4)
即
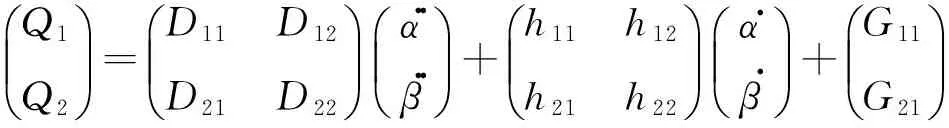
(5)
式中:D(q)为惯性矩阵,h(q,q..)为向心力和哥氏力矢量,G(q)为重力矢量.而向心力和哥氏力只对机器人高速运动有影响,在机器人低速运行时可以忽略.
2 约束分析
2.1 运动约束分析
码垛机器人的运动约束主要包括位移约束、速度约束和加速度约束.在一般运动情况下,只要保证位移不超限即可,这对轨迹规划的影响很小.这里主要考虑速度约束以及加速度约束,选取T型速度曲线进行运动约束分析.可以用下列不等式表示为
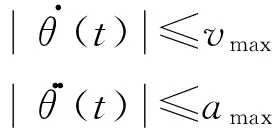
θ.(t)≤vmaxθ..(t)≤amax
(6)
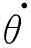

图2 速度约束的表示
图2的运动过程分为3个阶段:0~t1时刻为加速度为a的匀加速运动,t1~t2时刻为匀速运动,t2~tf时刻为减速度为a的匀减速运动.设初始时刻位置为θ0,可以建立运动学方程如下:
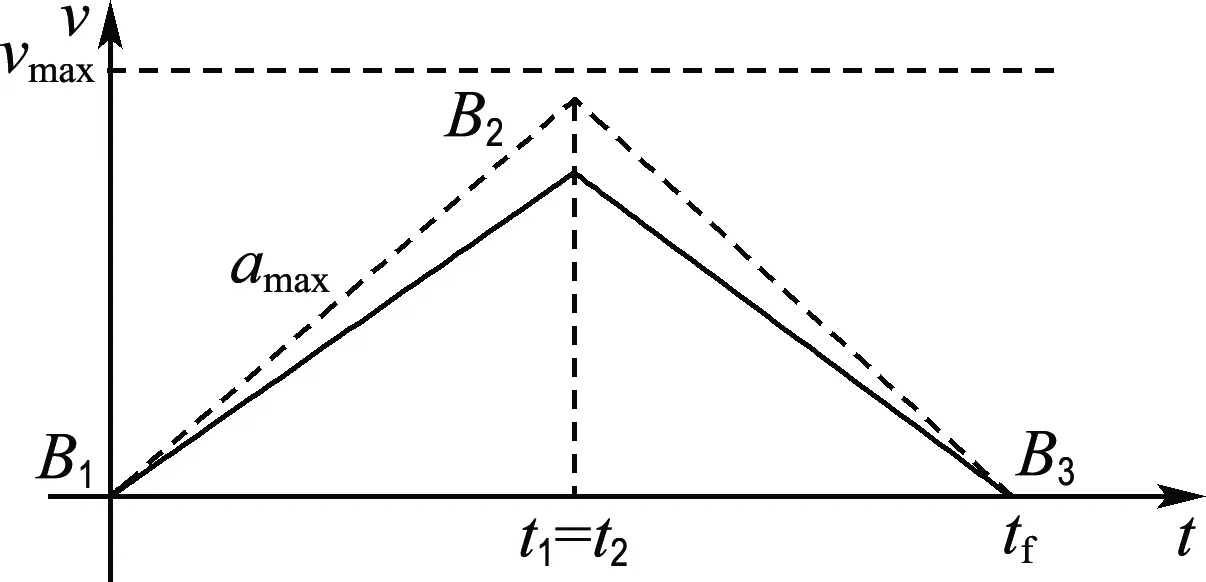
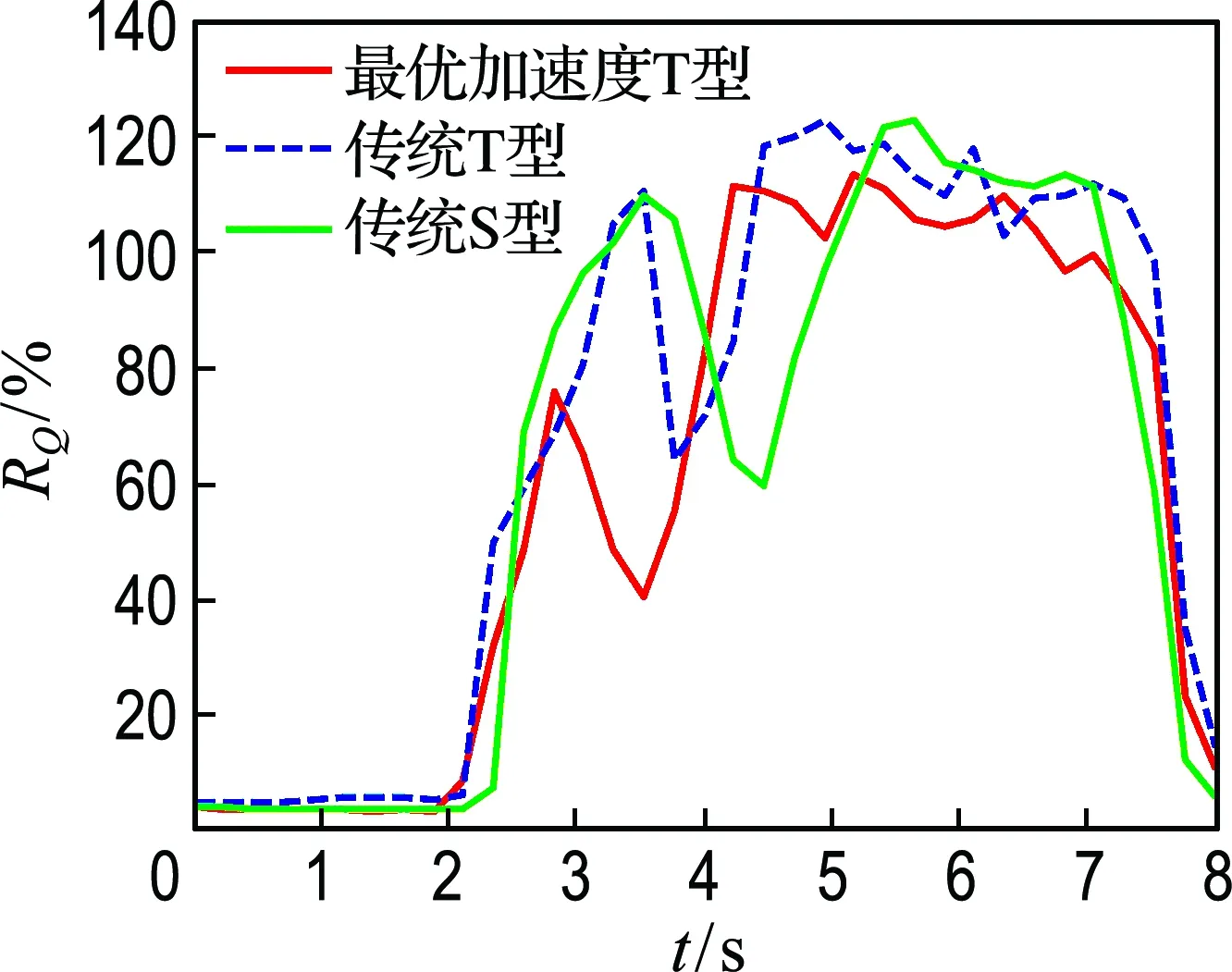
当0≤t θ..(t)=aθ.(t)=v0+at θ(t)=θ0+v0t+12at2 当t1≤t θ..(t)=0θ.(t)=v0+at1 θ(t)=θ0+(v0+at1)t-12at21 当t2≤t θ..(t)=-aθ.(t)=v0+at1-a(t-t2) θ(t)=θ0-12a(t21+t22+t2)+(v0+at1+at2)t 在终点时刻tf的位移为θf,可以得到关系式 (7) 在终点时刻tf的速度为vf,可以得到关系式 vf=v0+at1-a(tf-t2) (8) 在相同的位移、相同的时间内,加速度最小的轨迹驱动机构的驱动性能最优.当t1=t2时,整段轨迹只有加速段和减速段,此时求解的加速度唯一且为最小,非常利于运动的平稳性以及轨迹跟踪精度.但是,在具有约束的情况下,此时的速度很容易超过约束范围.所以,理想的轨迹规划应当是在满足约束的前提下,尽量采用较小的加速度. 2.2 运动约束处理 在相同的位移θf-θ0、相同的时间tf内,在没有任何约束的条件下,当t1=t2时,机器人的运动过程没有匀速段,机器人的加速度最小,机器人驱动性能最优. 图3 加速度约束 在式(7)、(8)中令t1=t2,得到 (9) 令θ0-θf+v0tf=c,由式(9)得, (10) 当vf=v0时,得 (11) 当vf≠v0时,令 (12) 可以得到 (13) 当式(13)中的t1、t2满足0≤t1=t2≤tf时才是正确的解,此时的加速度最优,其速度曲线如图4所示. 根据运动约束判断加速度a是否超过运动约束,若超过,则说明该驱动机构的驱动性能满足不了运动约束要求;若不超过,此时的加速度a以及相应的时间节点t1、t2构成的轨迹段,就是要求的满足运动约束的最优加速度轨迹. 图4 加速度约束下最优加速度图 图5 速度与加速度约束 由式(13)得到的是满足加速度约束的运动轨迹,这里在t达到一定程度后,速度v超过了最大速度vmax,运动过程中速度最大的阶段是在t1~t2的匀速运动阶段,此时的速度大小为vc=v0+at1.增大加速度a可以降低匀速运动阶段的速度vc,但是又不能超过最大加速度的限制,所以此时的最优加速度-速度曲线应如图6中的B1D1D2B3所示. 根据式(7)、(8),可以得到以下方程组: (14) 解得 (15) 若t1、t2满足0≤t1≤t2 图6 速度与加速度约束下最优加速度图 3.1 试验系统设计 如图7所示,码垛机器人的控制系统包括物料传送带的传动控制、机器人保护监测控制、回原点的运动控制以及码垛机器人的伺服控制.其中主控器采用大连理工计算机控制工程有限公司的四轴机器人运动控制器MAC1600,具有1路10/100M以太网通信接口、2路RS-485,支持单轴、多轴、轴组PLC_Open标准指令,支持直线、圆弧插补、多轴同步等多种运动控制算法,以高速脉冲的方式实现对驱动器进行精确速度控制、位置控制等功能,满足对码垛机器人控制的需求.采用PLC_Config软件对MAC1600进行梯形图编程完成系统运行中的逻辑控制,包括数据采集、外部I/O量的处理、伺服电机驱动、运动过程及运动轨迹的规划等.控制系统的电机选型如表1所示. 图7 总体控制方案 表1 伺服电机型号表 3.2 算法的单轴控制验证 调用运动控制指令中的单轴绝对定位指令MC_MoveAbsolute,该指令控制轴运动到指定的目标位置.控制机器人水平轴单轴运动,利用伺服器的RS-485通信功能,监控水平轴伺服驱动器的监控参数P0-01,该参数显示的是驱动器的输出转矩相对于额定转矩的百分比.单轴控制机器人分别在传统的T型、S型、最优加速度T型3种速度曲线下以相同的位姿运行相同的路程,得到3种情况下的力矩曲线如图8所示.横坐标表示时间,纵坐标表示力矩百分比. 图8 水平轴三种速度曲线下的输出力矩 图8中,红色曲线是机器人在最优加速度T型速度曲线控制下的驱动关节的力矩曲线,其运动过程中的力矩峰值相较于其他力矩曲线偏低.又由于其运动总时间相同,运动总位移相同,运动过程中姿态都相同,所以可以得到结论:在单轴控制中,最优加速度T型速度曲线控制下的驱动关节的驱动力矩相比传统的T型、S型速度曲线,在保证运动约束的同时,更能够发挥驱动关节的驱动性能. 3.3 算法的轴组控制验证 调用连续曲线运动控制指令,控制码垛机器人在8 s内完成一个抓货放货的标准门字型轨迹,其末端运动轨迹如图9所示. 图9 机器人末端动作图 配置封装好的MC_ContinuousCurve功能块中的引脚PointsArray为(2 100,0,-240,0)、(1 900,0,240,0)、(0,1 900,240,0)、(0,2 100,-240,0)4个型值点,分别表示抓货点、第一个途经点、第二个途经点以及放货点,配置运动总时间为8 s,利用伺服器的RS-485通信功能,同时分别监控腰部、水平、竖直轴伺服驱动器的力矩参数P0-01,采集数据,得到3种情况下的各个驱动轴的力矩曲线对比图,如图10~12所示.横坐标表示时间,纵坐标表示力矩百分比. 图10 轴组腰部轴力矩曲线对比 图中红色曲线是机器人在最优加速度T型速度曲线控制下的驱动关节的力矩曲线,其运动过程中的力矩峰值相较于其他力矩曲线偏低.又由于其运动总时间相同,运动总位移相同,运动过程中姿态都相同,所以可以得到结论:在轴组控制中,最优加速度T型速度曲线控制下的驱动关节的驱动力矩相比传统的T型、S型速度曲线,在保证运动约束的同时,更能够发挥驱动关节的驱动性能. 图11 轴组水平轴力矩曲线对比 图12 轴组竖直轴力矩曲线对比 本文以码垛机器人为研究对象,重点研究了机器人调试过程中遇到的运动超限问题,提出了一种加速度最优的、满足运动约束的T型速度曲线控制方法,在保证运动平稳的基础上,充分发挥驱动关节的驱动性能.详细介绍了机器人轨迹规划算法的原理及实现过程,最后,通过与传统速度曲线下的运动进行比较,证明无论单轴还是轴组,该最优加速度轨迹规划算法下的各个驱动关节的驱动性能最优.目前对码垛机器人的控制多数采用的仍是位置控制,接下来打算对通过力矩控制机器人运动的控制方法进行深入研究. [1] 徐海黎,解祥荣,庄 健,等. 工业机器人的最优时间与最优能量轨迹规划[J]. 机械工程学报, 2010, 46(9):19-25. XU Haili, XIE Xiangrong, ZHUANG Jian,etal. Global time-energy optimal planning of industrial robot trajectories [J]. Journal of Mechanical Engineering, 2010, 46(9):19-25. (in Chinese) [2] 丛 明,熊永康,刘 冬,等. 一种并联机械手操作空间最优时间轨迹规划方法[J]. 机械设计, 2016, 33(2):7-13. CONG Ming, XIONG Yongkang, LIU Dong,etal. A method of time-optimal trajectories planning for parallel robot operation space [J]. Journal of Machine Design, 2016, 33(2):7-13. (in Chinese) [3] LIN Chunshin, CHANG Porong, LUH J Y S. Formulation and optimization of cubic polynomial joint trajectories for industrial robots [J]. IEEE Transactions on Automatic Control, 1983, 28(12):1066-1074. [4] GASPARETTO A, ZANOTTO V. A technique for time-jerk optimal planning of robot trajectories [J]. Robotics and Computer-Integrated Manufacturing, 2008, 24(3):415-426. [5] 徐鹏飞,罗庆生,韩宝玲,等. 新型工业码垛机器人轨迹规划研究[J]. 组合机床与自动化加工技术, 2012(5):70-73,77. XU Pengfei, LUO Qingsheng, HAN Baoling,etal. Research on trajectory planning of new industrial palletizing robot [J]. Modular Machine Tool & Automatic Manufacturing Technique, 2012(5):70-73,77. (in Chinese) [6] 张丰华,韩宝玲,罗庆生,等. 基于PLC的新型工业码垛机器人控制系统设计[J]. 计算机测量与控制, 2009, 17(11):2191-2193, 2196. ZHANG Fenghua, HAN Baoling, LUO Qingsheng,etal. Control system design of palletizing robot based on PLC technology [J]. Computer Measurement & Control, 2009, 17(11):2191-2193, 2196. (in Chinese) [7] SARAVANAN R, RAMABALAN S, BALAMURUGAN C. Multiobjective trajectory planner for industrial robots with payload constraints [J]. Robotica, 2008, 26(6):753-765. [8] PIAZZI A, VISIOLI A. Global minimum-jerk trajectory planning of robot manipulators [J]. IEEE Transactions on Industrial Electronics, 2000, 47(1):140-149. [9] ZLAJPAH L, NEMEC B. Implementation of time-optimal path-tracking control on palletizing robots[J]. IEEE International Symposium on Industrial Electronics, 1999, 2:861-866. [10] GASPARETTO A, ZANOTTO V. Optimal trajectory planning for industrial robots [J]. Advances in Engineering Software, 2010, 41(4):548-556. [11] 张 斌. 基于多约束的机器人关节空间轨迹规划[J]. 机械工程学报, 2011, 47(21):1-6. ZHANG Bin. Joint-space trajectory planning for robots under multiple constraints [J]. Journal of Mechanical Engineering, 2011, 47(21):1-6. (in Chinese) [12] FAHHAM H R, FARID M, KHOORAN M. Time optimal trajectory tracking of redundant planar cable-suspended robots considering both tension and velocity constraints [J]. Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME, 2011, 133(1):011004. [13] PIRES J N, PAULO S. Robotic de-palletizing system for the non-flat ceramic industry [J]. Industrial Robot, 2003, 30(2):152-158. [14] PRASSE C, SKIBINSKI S, WEICHERT F,etal. Concept of automated load detection for de-palletizing using depth images and RFID data [C]// Proceedings — 2011 IEEE International Conference on Control System, Computing and Engineering, ICCSCE 2011. Piscataway:IEEE Computer Society, 2011:249-254. Research on robot trajectory planning algorithm with optimal acceleration ZHAO Liang*1, ZHONG Chongquan1, ZHENG Feixiang2 ( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China;2.HUAWEI Digital Technology Co., Ltd., Suzhou 215000, China ) In order to solve the problem of overrun in the process of robot debugging, a control method with optimal acceleration is proposed based on T type velocity curve under motion constraint. The dynamics performance of the palletizing robot is analyzed by using Lagrange method and the realization process of robot trajectory planning algorithm is discussed. This algorithm makes full use of the driving performance of the driving joint on the basis of smooth and stable movements. Compared with the traditional velocity curves, the control effect of the robot is significantly improved both in the single axis mode and the axis group mode. palletizing robot; dynamics; trajectory planning; optimal acceleration 2016-07-31; 2017-02-16. 国家自然科学基金资助项目(61472062);中央高校基本科研业务费专项资金资助项目(DUT15ZD230,DUT16RC(4)20);国家科技支撑计划资助项目(2015BAF20B02). 赵 亮*(1983-),男,博士,讲师, E-mail:zliang@dlut.edu.cn. 1000-8608(2017)02-0177-07 TH16;TP242 A 10.7511/dllgxb201702010

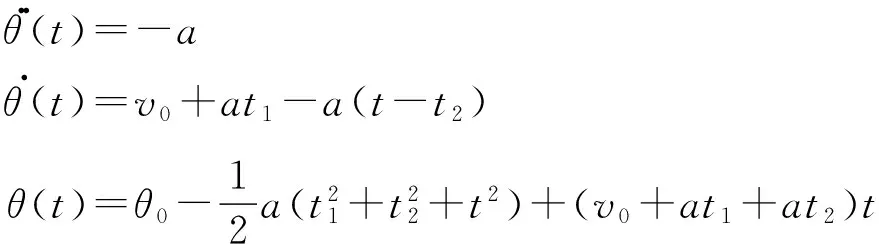

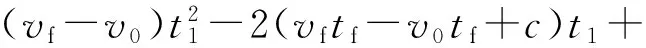


3 性能测试






4 结 语

