一种新的模糊稀疏表示人脸识别算法

李 懿， 刘 晓 东

( 1.大连理工大学 电子信息与电气工程学部 控制科学与工程学院, 辽宁 大连 116024；2.黑龙江科技大学 计算机与信息工程学院， 黑龙江 哈尔滨 150022 )

一种新的模糊稀疏表示人脸识别算法

李 懿1,2， 刘 晓 东*1

( 1.大连理工大学 电子信息与电气工程学部 控制科学与工程学院, 辽宁 大连 116024；2.黑龙江科技大学 计算机与信息工程学院， 黑龙江 哈尔滨 150022 )

稀疏表示人脸识别算法的主要思想是：一个未知的测试图像可以近似表示为所有与其隶属同类的训练样本的一个线性组合．然而，人脸之间存在着极大的相似性，同时易受到外部环境的影响，人脸分类的本身存在着一定的不确定性．针对这种不确定性，结合模糊集合理论，提出了一种新的模糊稀疏表示人脸识别算法．首先，引入一个非线性函数描述人脸的相似性程度．然后，基于该相似性度量以及最近邻分类器思想，定义一个自适应的模糊隶属度函数来分配人脸对类的隶属程度．而这一过程恰使得这些隶属度是稀疏化的．最后，将稀疏化的模糊隶属度作为训练样本表示测试样本的权值系数，进而重构测试图像．采用MATLAB在ORL和Yale人脸数据库上进行仿真实验，验证了该算法的有效性和稳定性．

人脸识别；模式识别；相似度；模糊隶属度；稀疏表示；最近邻分类器

0 引 言

人脸识别是一个热门的研究课题，近几十年来，被广泛应用于娱乐、信息安全以及司法等各个领域[1-2]．线性子空间分析算法是其中广受关注的特征提取与人脸识别算法之一．最著名的算法包括基于主成分分析(PCA)的特征脸算法[3]、Fisherface[4]、线性判别分析(LDA)[5]以及基于这些经典算法延伸出来的若干种改进算法．

另外一类新兴的人脸识别算法被称为稀疏化表示算法．该算法的基本思想是：用训练样本的一个稀疏化线性组合近似估计一个测试图像[6]．其中，稀疏即是在线性组合表示时，部分训练样本对应的系数为0．这类算法试图寻找不同类训练样本对测试图像潜在的贡献率．稀疏化表示算法不断涌现，例如：Gao等[7]提出的核稀疏表示的人脸识别算法以及Yang等[8]利用Gabor特征提出的稀疏表示分类器(SRC)等，验证了稀疏算法的识别精度高于非稀疏算法[9]．特别是基于l0-范数的凸规划算法进行的稀疏表示得到了较好的识别结果[10]．它将人脸识别问题看作一个多元线性规划模型的分类问题．首先，将一个测试图像用所有的训练样本稀疏化线性表示；然后，寻找最小表示误差的类记为该测试图像的类．然而，最小化l0-范数问题是一个NP难题，Wright等提出的鲁棒稀疏表示算法用l1-范数作为最近似于l0-范数的凸优化函数来解决这类稀疏化问题[11]．该算法指出稀疏信号表示的新理论可以为这类稀疏表示人脸识别算法提供关键的解决方案，并取得较好的实验结果[12-13]．尽管最小化l1-范数比最小化l0-范数更有效，但它仍然是一个非线性算法，算法复杂，时间代价较高．Xu等在文献[14]中提出了一个新的更为简单快速的稀疏表示人脸识别算法．该算法首先在每一类中选择与测试样本最近邻的训练样本；然后，用所有被选中的训练样本的一个线性组合近似估计测试图像．该算法证明了一个简单的稀疏表示人脸识别算法亦可得到较好的识别结果．

现有的这类算法中对类分配问题多停留在二分类基础上，即样本完全隶属于某一个类．换句话说，在确定模式类隶属度的过程中，每一个已标号的人脸在其中的重要性是均等的．然而，人脸数据在获取的过程中，样本往往会受到各种环境条件(如光照、姿势、年龄等)的影响，使得原始样本分布较为复杂．这种复杂性连同人脸本身具有的相似性和可变性等各种因素导致的不确定性都直接影响着人脸识别算法的识别精度．显然，在人脸分类时，这些影响因素应该被考虑进去．从本质上讲，考虑这些因素的人脸类分配问题应该是软分类，即模糊分类问题．换言之，一个给定标号的人脸可能部分地隶属于多个类[15]，而模糊集恰好可以处理这类近似推理、不确定性、模糊性和不精确性等问题[16]．

鉴于上述分析，结合模糊集合理论，本文提出一个新的模糊稀疏表示人脸识别算法(FSR)．首先，引入一个新的非线性函数描述人脸之间以及人脸与类之间的局部相似性程度．然后，基于相似性度量，定义一个自适应模糊集．该模糊集依据训练样本及最近邻思想确定人脸对类的一个稀疏化的模糊隶属度．这样的隶属度表示人脸与类之间的隶属程度，也表示训练样本对某一类人脸的表示能力．因此，以这些隶属度作为权值并近似地表示一个未知的测试图像是合理的，据此将测试图像辨识为重构误差最小的一类．与传统的最近邻概念不同，本算法中采用的是最大相似近邻．

1 算法思想

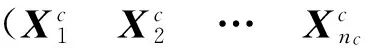
1.1 相似度函数的定义

为了定义一个恰当的模糊隶属度函数，首先定义相似性作为判别训练人脸之间以及人脸与类之间相似关系的度量．由于训练样本数量有限，联合概率密度函数通常是未知的．因此，类似于文献[17]，一个新的人脸局部相似性度量函数定义如下：

定义1(人脸相似度) 第i个人脸Xi和第j个人脸Xj之间的相似度定义为

(1)

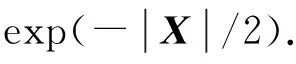
显然，该相似度函数是关于样本对的灰度值差值的减函数，两个人脸相对应的灰度值越接近，相似度值越大，进而表示人脸越相似．与传统的核函数不同，它是在样本对之间独立计算的，因此，它是表示两个随机变量之间的一个局部相似性的度量．

(2)

1.2 自适应模糊集

一般地，模糊集合理论可以处理模式与类之间不确定的隶属关系问题．假设给定一个训练样本X，它的一个s划分可以给训练样本对s个类分别分配一个隶属度，这种隶属度在0～1变化，而同一个模式隶属于各类的程度之和应该为1．因此，模糊隶属度矩阵U=(μl1l2)应该满足如下性质：

(3)

(4)

其中μl1l2∈[0,1]．

对于人脸模式的软分类问题可以追溯到Keller等发表的公开结果[18]，其理论基础是模糊k-近邻分类算法，即对于给定的模式Xj，隶属于c类的近邻越多，隶属于c类的程度越大．因此，基于相似性度量及k-近邻分类思想，本文定义了一个自适应模糊集．

(5)

其中label(j)=c表示Xj给定的类标号为c．

事实上，上述隶属度分配算法试图模糊化或改善已标号模式的隶属度，而模式的主隶属度并没有受到影响，即已标号的人脸模式没有被完全地划分为其他类．该定义只是对隶属度进行了某些细化或改善，并且保证了所得隶属度是稀疏化的．由于模糊隶属度可以指代样本对类的贡献程度，用这样的隶属度作为表示测试样本的权值系数是合理的．本文算法正是在这种软分类的基础上实现了人脸的识别．

1.3 分类器

本文试图采用训练样本集合的一个稀疏的线性组合尽可能好地近似表示一个未知的样本y．从理论上看，与y同类的训练样本才可能对y给出一个最佳的重构估计．因此，根据相似性及模糊隶属度，对一个测试样本y的分类过程如下：

对每一个c类，令δc(β)为隶属度向量，即δc(β)=(μ(c,j))(j=1,2,…,N，c=1,2,…,s)，则给定的样本y相对于c类的近似估计为

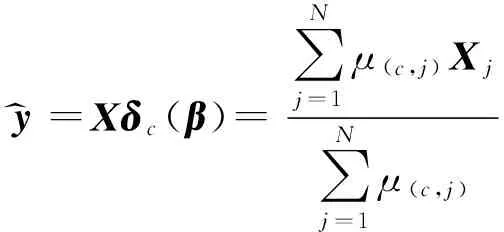
y^=Xδc(β)=∑Nj=1μ(c,j)Xj∑Nj=1μ(c,j)

(6)

y被认为是所有类对应的重构中，估计误差最小的那个类中的样本，即

(7)

综上所述，新的模糊稀疏化表示的人脸识别算法(FSR)的具体步骤归纳如下：

步骤3 按照式(5)计算模糊隶属度μ(c,j)．

步骤4 将模糊隶属度μ(c,j)作为稀疏化权值系数．在新的分类基础上，按式(6)将测试图像y重构为

=Xδc(β)；c=1,2,…,s

步骤5 计算估计误差：

步骤6 识别y为估计误差最小的一类，即

2 实 验

为了验证本文算法的有效性和稳定性，针对人脸公开数据库ORL(由英国剑桥大学AT&T实验室提供)和Yale(由美国耶鲁大学计算视觉与控制中心创建)进行MATLAB仿真．将FSR算法与经典的稀疏表示算法(SRC)、经典的模糊人脸识别算法(FLDA)的实验结果进行对比．在实验中，训练样本都是随机选取的，并选择除训练样本外的其余样本作为测试样本．记录10次随机实验的平均识别结果进行比较．另外，所有的度量函数均在人脸矩阵基础上计算，不需要将人脸数据转换为向量，一定程度上减少了算法的复杂性．

2.1 ORL人脸数据库实验结果

ORL人脸数据库包含了40个人的400张人脸图像，这些图像伴随着位置、方向、人脸表情(睁眼或闭眼、笑或不笑)以及人脸细节(戴眼镜或不戴眼镜)等方面的变化．数据中所有灰度图像首先被标准化为92 pixels×112 pixels．在对ORL人脸数据库进行的实验中，训练样本的个数在3～7变化，且参数k等于相应的训练样本个数．10次随机实验的平均识别精度R如图1所示．

图1 FSR算法与SRC、FLDA算法对ORL人脸数据库的识别精度

Fig.1 Recognition accuracy on ORL face database for FSR, SRC and FLDA algorithms

2.2Yale人脸数据库实验结果

Yale人脸数据库由15个人的165张人脸图像组成．其中，每个个体的图像个数为11．所有图像在不同的光照环境下采集，并且包含了一系列表情变化，如悲伤、喜悦等．本文算法中使用的图像均是标准化为231pixels×192pixels的灰度图像．实验中，训练样本个数在3～7变化，参数k等于训练样本个数．10次随机实验的平均识别精度R如图2所示．

图1和图2表明，本文算法的识别精度始终优于其他经典的人脸识别算法(包括FLDA、SRC等)，识别精度提高2%以上．随着样本个数的增加，FSR算法的识别精度提高速度加快，并趋于稳定．

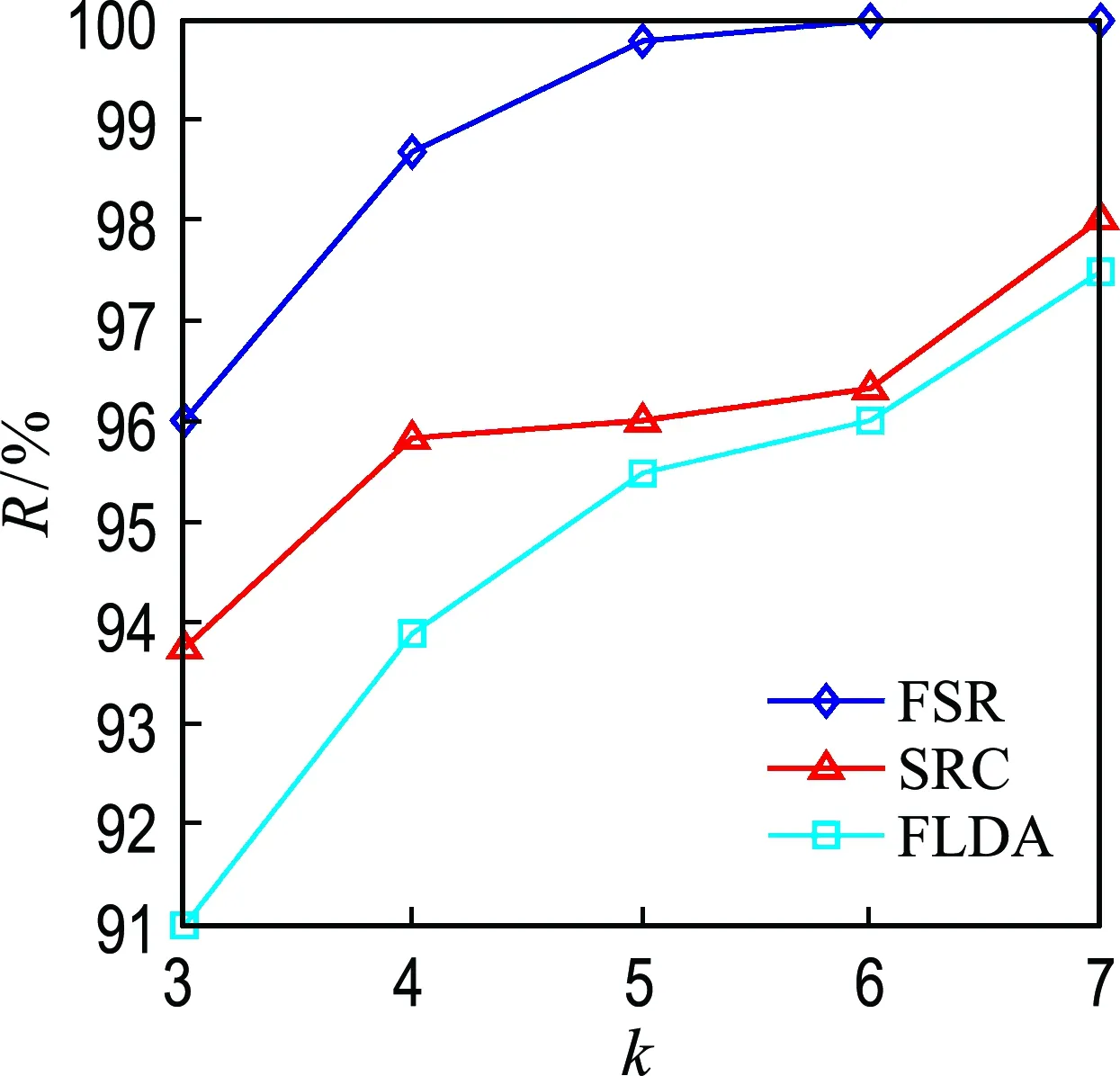
图2FSR算法与SRC、FLDA算法对Yale人脸数据库的识别精度

Fig.2 Recognition accuracy on Yale face database for FSR, SRC and FLDA algorithms

2.3 算法时间复杂性对比结果

针对ORL和Yale人脸数据库，本文对算法的时间复杂性进行了对比分析．各算法的时间消耗对比如表1、2所示．其中，FSR算法运行消耗的时间不及SRC算法的1/10．可见，本文算法不仅有效地改善了人脸识别的精度，而且大大提高了时间运行效率．

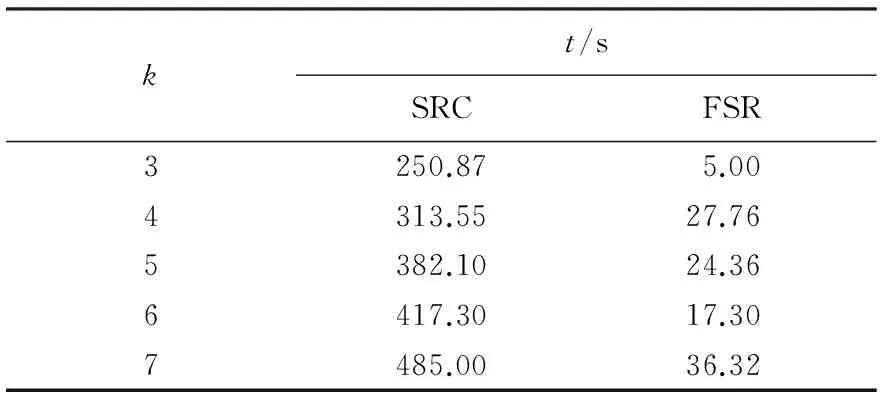
表1 基于ORL人脸数据库的时间消耗

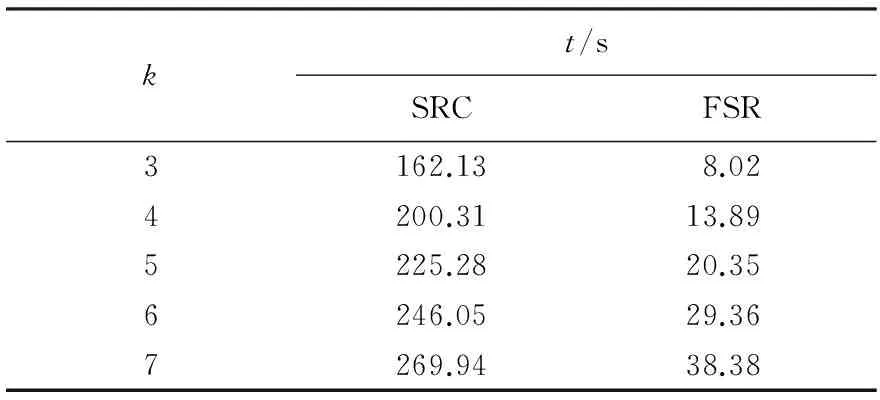
表2 基于Yale人脸数据库的时间消耗

3 结 语

本文主要研究一个模糊的稀疏表示人脸识别算法(FSR)．该算法基于一个新的相似性度量以及k-近邻分类思想，定义了一个新的自适应模糊隶属度函数．该模糊隶属度函数使训练样本对应的类隶属度是模糊的且稀疏化的．以这种稀疏的模糊隶属度表示训练样本对类的贡献率，对测试样本进行近似估计，并将估计误差最小的类辨识为测试图像所属类．

FSR算法是一种新的且有效的模糊稀疏表示人脸识别算法．利用新提出的相似性度量，并结合最相似k-近邻分类思想来确定重构测试图像的权值系数，简化了稀疏表示算法过程，同时，避免了凸规划模型的求解问题，大大提高了算法的时间效率．最相似k-近邻分类思想的引入，可以有效地利用人脸相似性等客观因素对于人脸数据的影响，提高识别精度．该算法是一种模糊算法，有效地避免了以往算法中人脸二分类的弊端．

采用MATLAB进行仿真实验，实验结果表明FSR算法与经典人脸识别算法相比，识别精度始终较高，而且时间复杂性相对较小．可见，这种新的稀疏模糊隶属度可以较好地修正对测试图像线性估计的结果，同时极大地减少了算法的时间代价．

[1] KWAK K C, PEDRYCZ W. Face recognition using a Fuzzy Fisherface classifier [J]. Pattern Recognition, 2005, 38(10):1717-1732.

[2] ZHU Ningbo, LI Shengtao. A kernel-based sparse representation method for face recognition [J]. Neural Computing and Applications, 2014, 24(3-4):845-852.

[3] TURK M, PENTLAND A. Eigenfaces for recognition [J]. Journal of Cognitive Neuroscience, 1991, 3(1):71-86.

[4] BELHUMEUR P N, HESPANHA J P, KRIEGMAN D J. Eigenfaces vs. Fisherfaces: recognition using class specific linear projection [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1997, 19(7):711-720.

[5] MITCHELL H B. Image sub-space techniques [M] // Image Fusion. Berlin: Springer Berlin Heidelberg, 2010:107-124.

[6] ELHAMIFAR E, VIDAL R. Sparse subspace clustering [C] // 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops 2009. Piscataway: IEEE Computer Society, 2009:5206547.

[7] GAO Shenghua, TSANG I W H, CHIA L T. Kernel sparse representation for image classification and face recognition [C] // Computer Vision, ECCV 2010 — 11th European Conference on Computer Vision, Proceedings. Heidelberg: Springer Verlag, 2010:1-14.

[8] YANG Meng, ZHANG Lei. Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary [C] // Computer Vision, ECCV 2010 — 11th European Conference on Computer Vision, Proceedings. Heidelberg: Springer Verlag, 2010:448-461.

[9] WAGNER A, WRIGHT J, GANESH A,etal. Towards a practical face recognition system:robust registration and illumination by sparse representation [C] // 2009 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Workshops, CVPR Workshops 2009. Piscataway: IEEE Computer Society, 2009:5206654.

[10] TROPP J A, WRIGHT S J. Computational methods for sparse solution of linear inverse problems [J]. Proceedings of the IEEE, 2010, 98(6):948-958.

[11] WRIGHT J, YANG A Y, GANESH A,etal. Robust face recognition via sparse representation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(2):210-227.

[12] DEBRUYNE M, VERDONCK T. Robust kernel principal component analysis and classification [J]. Advances in Data Analysis and Classification, 2010, 4(2):151-167.

[13] XU Yong, ZHANG D, JIN Zhong,etal. A fast kernel-based nonlinear discriminant analysis for multi-class problems [J]. Pattern Recognition, 2006, 39(6):1026-1033.

[14] XU Yong, ZHU Qi. A simple and fast representation based face recognition method [J]. Neural Computing and Applications, 2013, 22(7-8):1543-1549.

[15] WANG Jianguo, YANG Wankou, YANG Jingyu. Face recognition using fuzzy maximum scatter discriminant analysis [J]. Neural Computing and Applications, 2013, 23(3-4):957-964.

[16] ZADEH L A. Fuzzy sets [J]. Information and Control, 1965, 8(3):338-353.

[17] HE Ran, ZHENG Weishi, HU Baogang. Maximum correntropy criterion for robust face recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(8):1561-1576.

[18] KELLER J M, GRAY M R, GIVENS J A. Fuzzyk-nearest neighbor algorithm [J]. IEEE Transactions on Systems, Man, and Cybernetics, 1985, SMC-15(4):580-585.

A new fuzzy sparse representation algorithm for face recognition

LI Yi1,2, LIU Xiaodong*1

( 1.School of Control Science and Engineering, Faculty of Electronic Information and Electrical Engineering,Dalian University of Technology, Dalian 116024, China；2.School of Computer and Information Engineering, Heilongjiang University of Science and Technology,Harbin 150022, China )

The main idea of a sparse representation-based face recognition algorithm is that an unknown test sample is approximately represented as a linear combination of all the training samples corresponding to the same class with it. However, the classification of faces may possess some uncertainty, because there is a great similarity among faces and they are easy to be affected by environmental conditions. Based on this uncertainty and fuzzy theory, a new fuzzy sparse representation (FSR) algorithm for face recognition is proposed. Firstly, a new nonlinear function is introduced to represent the similarity among faces. Then, based on the similarity measurement and the nearest neighbors classifier, an adaptive fuzzy membership function is defined, which produces the corresponding membership degree to the class. During this process, the membership degree is sparsity. Finally, the sparse fuzzy membership degree is taken as the weight coefficients of training samples to express test samples to restructure the test image. Utilizing MATLAB, the experiments conducted on the ORL and Yale face databases have demonstrated the effectiveness and robustness of the proposed algorithm.

face recognition; pattern recognition; similarity; fuzzy membership degree; sparse representation; the nearest neighbors classifier

2016-05-23；

2017-01-12．

国家自然科学基金资助项目(61175041).

李 懿(1980-)，女，博士生，E-mail:liyi_80s@163.com；刘晓东*(1963-)，男，教授，博士生导师，E-mail:xdliuros@hotmail.com.

1000-8608(2017)02-0189-06

TP391.41

A

10.7511/dllgxb201702012